6.5一次函数的应用(2) 导学案

中小学教育资源及组卷应用平台
6.5一次函数的应用(2)
【学习目标】
1.提高学生的读图能力，解决与两个一次函数相关的图象信息题；
2.进一步培养学生数形结合思想，以及分析、解决问题的能力，提高思维能力.
【课前梳理】
自学课本第164至166页的内容，思考并解答下列问题。
1.一次函数的图像与性质
2.确定一次函数的表达式
【课堂练习】
知识点一 一次函数的应用
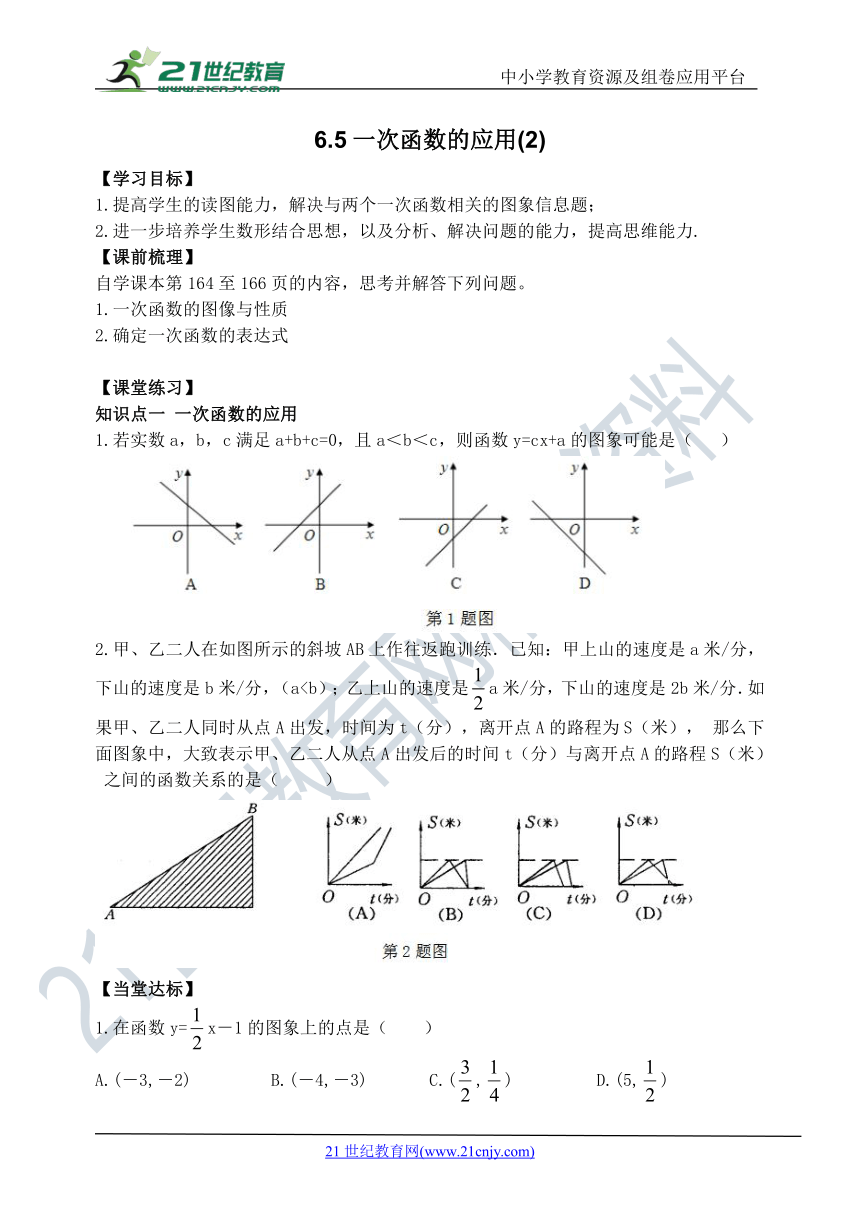
1.若实数a，b，c满足a+b+c=0，且a＜b＜c，则函数y=cx+a的图象可能是（ ）
2.甲、乙二人在如图所示的斜坡AB上作往返跑训练．已知：甲上山的速度是a米/分，下山的速度是b米/分，（a【当堂达标】
1.在函数y=x－1的图象上的点是（ ）
A.(－3,－2) B.(－4,－3) C.(,) D.(5,)
2.如果一个正比例函数的图象经过点A（3，－1），那么正比例函数的解析式为（ ）
A.y=3x B.y=－3x C.y=x D.y=－x
3.直线 y=x＋4与 x轴交于 A，与y轴交于B, O为原点，则△AOB的面积为（ ）
A.12 B.24 C.6 D.10
4.一次函数y＝－2x＋1的图象不经过下列哪个象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若点（m，n）在函数y=-x+2的图象上，则m，n之间的关系式是
【课后拓展】
1.如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.
⑴ 求A，B两点的坐标；
⑵ 过B点作直线BP与x轴相交于P，且使OP=2OA， 求ΔABP的面积.
2.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米．
(2)兔子在起初每分钟跑多少米 乌龟每分钟爬多少米
(3)乌龟用了多少分钟追上了正在睡觉的兔子
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟
6.5一次函数的应用（2）
【课堂练习】
1.C 2.C
【当堂达标】
1.B 2.D 3.C 4.C 5.n=-m+2
【课后拓展】
1.解:(1)当y=0时,2x+3=0,解得x=,则A点坐标为（，0）;
当x=0时,y=2x+3=3,则B点坐标为（0,3）;
(2)∵OP=2OA,
∴P点坐标为（3，0）或（-3,0）,
∴AP=或,
∴
或.
故答案为:或.
2.解:(1)兔子、乌龟、1500;
(2)结合图象得出:兔子在起初每分钟跑700米.
1500÷30=50米
乌龟每分钟爬50米.
(3)700÷50=14(分钟)
乌龟用了14分钟追上了正在睡觉的兔子.
(4)48千米=48000米
48000÷60=800(米/分)
（1500-700）÷800=1(分钟)
30+0.5-12=28.5(分钟)
兔子中间停下睡觉用了28.5分钟.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)