第二十章:数据的分析练习题(含解析)2021-2022学年江西省八年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第二十章:数据的分析练习题(含解析)2021-2022学年江西省八年级下学期人教版数学期末试题选编 |

|
|
| 格式 | zip | ||
| 文件大小 | 447.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 00:00:00 | ||
图片预览




文档简介
第二十章:数据的分析 练习题
一、单选题
1.(2022春·江西南昌·八年级统考期末)从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
2.(2022春·江西上饶·八年级统考期末)某次数学测验中,八(1)班55人平均分为80分,八(2)班45人平均分为70分,则这两个班总平均分为( )
A.75分 B.75.5分 C.76分 D.76.5分
3.(2022春·江西宜春·八年级统考期末)一组数据:的平均数为,众数为,中位数为,则以下判断正确的是( )
A.一定出现在中 B.一定出现在中
C.一定出现在中 D.,,都不会出现在中
4.(2022春·江西赣州·八年级统考期末)为了解某公司员工的年工资情况,小王随机调查了10位员工,某年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20.下列统计量中,能合理反映该公司员工年工资水平的是( )
A.方差 B.众数 C.中位数 D.平均数
5.(2022春·江西宜春·八年级统考期末)根据疫情防控的要求,学校对所有进入校园的师生进行体温检测,其中7名学生的体温(单位)如下:36.6,36.7,36.6,36.4,36.6,36.5,36.7,这组数据的众数和中位数分别是( )
A.36.6,36.4 B.36.6,36.6 C.36.7,36.4 D.36.7,36.6
二、填空题
6.(2022春·江西赣州·八年级统考期末)若一组数据7,6,m,10,9的平均数为8,则m=_____.
7.(2022春·江西新余·八年级统考期末)已知一组数据,,,,的平均数是3,则数据,,,,的平均数是________.
8.(2022春·江西新余·八年级统考期末)现有甲、乙两种糖果的单价与千克数如下表所示.
甲种糖果 乙种糖果
单价(元/千克) 30 20
千克数 2 3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为______元/千克.
9.(2022春·江西宜春·八年级统考期末)南吕是国家历史文化名城,其名源于“昌大南疆,南方昌盛”之意,市内的滕王阁、八一起义纪念馆、海昏侯遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴.某班同学分小组到以上五个地方进行研学,人数分别为:12,5,11,5,7(单位:人),这组数据的中位数是______.
10.(2022春·江西吉安·八年级统考期末)为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况,将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图,根据提供的数据,该班50名同学一周参加体育锻炼时间的中位数是_____,众数是_____.
11.(2022春·江西南昌·八年级统考期末)若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为___________.
12.(2022春·江西赣州·八年级统考期末)已知一个样本1,3,2,2,a,b,c的众数为3,平均数为2,则该样本的方差为___.
13.(2022春·江西上饶·八年级统考期末)甲、乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差s2甲与s2乙的大小关系是s2甲_______s2乙.(填“>”或“<”)
14.(2022春·江西南昌·八年级统考期末)“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则______品种更适合在该村推广.(填“甲”或“乙”)
三、解答题
15.(2022春·江西赣州·八年级统考期末)学校团委组织了一次“中国梦·航天情”系列活动.下面是八年级甲,乙两个班各项目的成绩(单位:分):
项目班次 知识竞赛 演讲比赛 版面创作
甲 85 91 88
乙 90 84 87
(1)如果根据三项成绩的平均分计算最后成绩,请通过计算说明甲、乙两班谁将获胜;
(2)如果将知识竞赛、演讲比赛、版面创作按5:3:2的比例确定最后成绩,请通过计算说明甲乙两班谁将获胜.
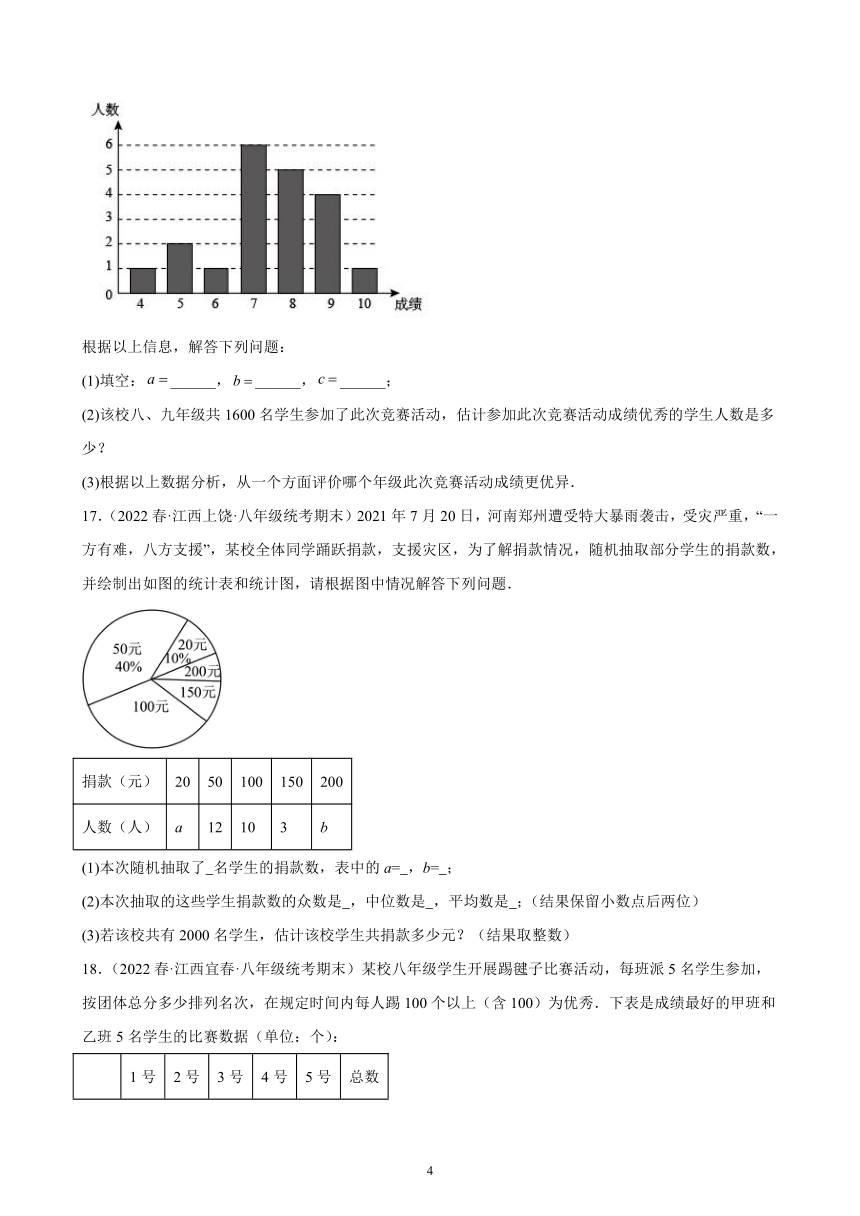
16.(2022春·江西赣州·八年级统考期末)为了解学生掌握垃圾分类知识的情况,增强学生环保意识,某学校举行了“垃圾分类人人有责”的知识竞赛活动.现从该校八、九年级中各随机抽取20名学生的竞赛成绩(满分10分,6分及6分以上为合格,8分及8分以上为优秀)进行整理、描述和分析,下面给出了部分信息:
九年级20名学生的竞赛成绩为:3,5,7,6,9,8,6,7,10,9,8,8,6,6,8,8,8,9,9,8.
八、九年级抽取的学生的竞赛成绩统计表
八年级20名学生的竞赛成绩条形统计图
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)该校八、九年级共1600名学生参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
(3)根据以上数据分析,从一个方面评价哪个年级此次竞赛活动成绩更优异.
17.(2022春·江西上饶·八年级统考期末)2021年7月20日,河南郑州遭受特大暴雨袭击,受灾严重,“一方有难,八方支援”,某校全体同学踊跃捐款,支援灾区,为了解捐款情况,随机抽取部分学生的捐款数,并绘制出如图的统计表和统计图,请根据图中情况解答下列问题.
捐款(元) 20 50 100 150 200
人数(人) a 12 10 3 b
(1)本次随机抽取了 名学生的捐款数,表中的a= ,b= ;
(2)本次抽取的这些学生捐款数的众数是 ,中位数是 ,平均数是 ;(结果保留小数点后两位)
(3)若该校共有2000名学生,估计该校学生共捐款多少元?(结果取整数)
18.(2022春·江西宜春·八年级统考期末)某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 2号 3号 4号 5号 总数
甲班 120 118 130 109 123 600
乙班 109 120 115 139 117 600
经统计发现两班总数相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)填空:甲班的优秀率为_________,乙班的优秀率为_________;
(2)填空:甲班比赛数据的中位数为_________,乙班比赛数据的中位数为_________;
(3)根据以上两条信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
19.(2022春·江西上饶·八年级校联考期末)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
20.(2022春·江西赣州·八年级统考期末)“五项管理”、“双减”政策的出台和落实为家校管理、学生减负带来了较好的成效.教育部门为进一步了解“双减”后初中学生每天在校体育活动的时间(单位:),随机调查了某校的部分初中学生.根据调查结果,绘制出如下的统计图和图.请根据相关信息,解答下列问题:
(1)本次接受调查的初中学生人数为______,图中的值为______;
(2)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(3)根据统计的这组每天在校体育活动时间的样本数据,若该校共有名初中学生,估计该校每天在校体育活动时间大于的学生人数.
21.(2022春·江西上饶·八年级统考期末)某校对八(1)班学生所穿校服型号情况进行了调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号).
根据以上信息,解答下列问题:
(1)八(1)班学生共______人,这组数据中的众数是______,中位数是_____;
(2)在条形统计图中,请把空缺部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小,
22.(2022春·江西赣州·八年级统考期末)某实验基地为了考察甲、乙两种小麦的长势,分别从中抽取10株麦苗,测得苗高如下(单位:cm):
甲 12 13 14 13 10 16 13 13 15 11
乙 6 9 7 12 11 16 14 16 20 19
(1)将数据整理,并通过计算后把下表填全:
小麦 中位数 众数 平均数 方差
甲 13 b 13 2.8
乙 a 16 c 21
________,________,________.
(2)若实验基地有甲种小麦2000株,请你估计甲种小麦苗高不低于13cm的株数.
(3)请你选择合适的数据代表,说明哪一种小麦长势较好.
23.(2022春·江西新余·八年级统考期末)每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共1200名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
七年级抽取的学生的竞赛成绩:
4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)根据以上数据分析,从中位数来看,______年级成绩更优异;从合格率来看,______年级成绩更优异;从方差来看,______年级成绩更整齐;
(3)估计该校七、八年级共1200名学生中竞赛成绩达到9分及以上的约有多少人?
24.(2022春·江西上饶·八年级校联考期末)同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图8是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cmabcdefgh20cm,且 pq),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
参考答案:
1.B
【详解】由题意知,a个x1的和为ax1,b个x2的和为bx2,c个x3的和为cx3,数据总共有a+b+c个,所以这个样本的平均数=,故选B.
2.B
【分析】求出各班的总分,再求出其平均数即可.
【详解】解:这两个班总平均分为=75.5(分)
故选B.
【点睛】此题主要考查平均数的求解,解题的关键是熟知加权平均数的计算方法.
3.B
【分析】根据平均数、中位数、众数的定义,对于错误的说法举出反例说明,从而利于排除法求解.
【详解】解:A、如数据0,1,1,4这四个数的平均数是1.5,不是这组数中的某个数,错误,不符合题意;
B、众数是一组数据中出现次数最多的数,它一定是数据中的数,正确,符合题意;
C、如数据1,2,3,4的中位数是2.5,不是这组数中的某个数,错误,不符合题意;
D、众数是一组数据中出现次数最多的数,它一定是数据中的数,错误,不符合题意.
故选:B.
【点睛】本题主要考查了平均数、中位数、众数的定义.平均数等于数据之和除以总个数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
4.C
【分析】根据中位数的定义求解.
【详解】解:中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),反映的是一组数据的中间水平.因此能合理反映该公司年工资中等水平的是中位数.
故选C.
5.B
【分析】这组数据从小到大排列,再根据众数和中位数的概念求解可得.
【详解】解:将这组数据重新排列为36.4,36.5,36.6,36.6,36.6,36.7,36.7,
所以这组数据的众数为36.6,中位数为36.6,
故选:B.
【点睛】本题主要考查众数和中位数,解题的关键是掌握求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
6.8
【分析】根据平均数的定义列出方程,解方程即可求解.
【详解】解:∵一组数据7,6,m,10,9的平均数为8,
∴,
解得.
故答案为:8.
【点睛】本题考查了已知平均数求未知数据的值,掌握平均数的求法是解题的关键.
7.5
【分析】根据平均数的变化规律可得:数据,,,,的平均数是2×3 1.
【详解】解:∵数据x1,x2,x3,x4,x5的平均数是3,
∴数据,,,,的平均数是2×3 1=5,
故答案为:5.
【点睛】本题考查的是算术平均数的求法及运用,熟记平均数的计算公式是解题的关键.
8.24
【分析】根据题意及加权平均数的求法可直接进行求解.
【详解】解:由题意得:
(元/千克);
故答案为24.
【点睛】本题主要考查加权平均数,熟练掌握加权平均数的求法是解题的关键.
9.7
【分析】根据题意,将已知数据从小到大排列,根据中位数的定义即可求解.中位数:把一组数据按从小到大的顺序排列,在中间的一个数字(或者两个数字的平均值)叫做这组数据的中位数.
【详解】将12,5,11,5,7从小到大排列:5,5,7,11,12;
则中位数为.
故答案为:.
【点睛】本题考查了求一组数据的中位数,理解中位数的定义是解题的关键.
10. 9 8.
【分析】根据众数和中位数的定义求解.
【详解】8是出现次数最多的,故众数是8,
这组数据从小到大的顺序排列,处于中间位置的两个数都是9,故中位数是9,
故答案为9;8.
【点睛】本题属于基础题,考查了确定一组数据的中位数和众数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
11.16
【分析】根据已知条件分析,得出x和y中有一个数为21,再根据中位数得出另一个数,从而求出平均数.
【详解】解:∵一组数据21,14,x,y,9的众数和中位数分别是21和15,
若x=y=21,则该组数据的中位数为:21,不符合题意,
则x和y中有一个数为21,另一个数为15,
∴这组数据的平均数为:(9+14+15+21+21)÷5=16,
故答案为:16.
【点睛】本题考查了平均数,中位数,众数的概念,解题的关键是掌握相应的求法.
12.
【详解】因为众数为3,不妨设a=b=3,则1+3+2+2+3+3+c=2×7,所以c=0,
所以方差为.
故答案为.
13.>
【分析】利用方差反映一组数据的波动大小的一个量进行判断.
【详解】解:∵甲地日平均气温的比乙地的日平均气温的变化幅度大,
∴方差s2甲>s2乙.
故答案为>.
【点睛】本题考查了方差:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
14.乙
【分析】由甲,乙的平均数相同,不好比较,但是甲的方差远远大于乙的方差,根据方差的含义分析可得答案.
【详解】解: /亩,﹐/亩,,
从平均数上看,甲,乙相同,但是甲的方差远远大于乙的方差,所以甲品种的稳定性比乙差,
则乙品种更适合在该村推广.
故答案为:乙.
【点睛】本题考查的是利用平均数,方差的含义做决策,掌握平均数与方差的含义是解题的关键.
15.(1)甲班将获胜
(2)乙班将获胜
【分析】(1)根据表格中的数据和平均数的计算方法可以解答本题;
(2)根据加权平均数的计算方法可以解答本题.
(1)
甲班的平均分为:(85 +91 + 88) ÷3= 88(分),
乙班的平均分为:(90 +84+87) + 3= 87(分),
∵88>87,
∴甲班将获胜;
(2)
由题意可得:
甲班的平均分为: (分),
乙班的平均分为:=87.6(分),
∵87.4 < 87.6,
∴乙班将获胜.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
16.(1)7;7.5;85%
(2)880
(3)九年级,理由见解析
【分析】(1)根据题目中的数据和条形统计图中的数据,可以得到a、b、c的值;
(2)先分别求出两个年级成绩优秀的学生人数,再用全校总人数乘以两个年级成绩优秀人数占抽取的两个年级的总人数的比值,即可求解;
(3)从比较众数、中位数,合格率大小可得答案.
【详解】(1)解:由条形图可得,得7分的人数最多,有6人,
所以八年级成绩的众数为7,故a=7,
八年级成绩从小到大排列,第10个与第11个成绩为7分和8分,
所以八年级成绩的中位数是=7.5分,故b=7.5,
八年级成绩6分及6分以上的有1+6+5+4+1=17(人),
所以八年级成绩的合格率为,故c=85%,
故答案为:7;7.5;85%.
(2)解:八年级成绩优秀的人数为:5+4+1=10(人),
九年级成绩优秀的人数为:12人,
1600×=880(人),
答:估计参加此次竞赛活动成绩优秀的学生人数是880人.
(3)解:从众数、中位数,合格率看,都要是九年级大,所以九年级此次竞赛活动成绩更优异.
【点睛】本题考查条形统计图,中位数、众数、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
17.(1)30,3,2
(2)50,75,88.67
(3)估计该校学生共捐款约177340元.
【分析】(1)根据捐款50元的人数和所占的百分比可以求得本次抽查的学生数,进而可以计算出a和b;
(2)根据(1)中补充完整的统计表可以得到本次调查获取的样本数据的众数、中位数和平均数;
(3)根据(2)中的平均数可以计算出该校2000名学生共捐款数.
(1)
解:12÷40%=30(名),
a=30×10%=3(人),
b=30-3-12-10-3=2(人),
故答案为:30,3,2;
(2)
解:由统计表可知,
捐50元的人数12人,人数最多,则众数是50元,
排在第15、16位两个数是50和100,
则中位数是=75(元),
平均数是:88.67(元);
故答案为:50,75,88.67;
(3)
解:2000×88.67=177340(元),
估计该校学生共捐款约177340元.
【点睛】本题考查统计表、扇形统计图、用样本估计总体、中位数、众数和加权平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
18.(1)100%,100%
(2)120,117
(3)将冠军奖状发给甲班,因为甲班5人比赛成绩的优秀率等于乙班,但中位数比乙班大,综合评定甲班比较好
【分析】(1)优秀率就是优秀的人数与总人数的百分比;
(2)中位数就是一组数据中先把所有数据按从大到小或从小到大的顺序排列起来,如果是奇数个时,就是中间的那一个数,如果是偶数个时,就是中间两个数的平均数;
(3)根据计算出来的统计量的意义分析判断.
【详解】(1)解:甲班优秀率为100%,乙班优秀率为100%,
故答案为:100%,100%;
(2)解:甲班5名学生比赛成绩的中位数是120个,乙班5名学生比赛成绩的中位数是117个,
故答案为:120,117;
(3)解:将冠军奖状发给甲班,因为甲班5人比赛成绩的优秀率等于乙班,但中位数比乙班大,综合评定甲班比较好.
【点睛】本题考查统计初步的数据处理能力,涉及优秀率概念、中位数的概念和根据数据分析做决策等知识,熟练掌握相关定义并运用它的意义解决问题是本题关键.
19.(1)16,17;(2)14;(3)2800.
【分析】(1)将数据按照大小顺序重新排列,计算出中间两个数的平均数即是中位数,出现次数最多的即为众数;
(2)根据平均数的概念,将所有数的和除以10即可;
(3)用样本平均数估算总体的平均数.
【详解】(1)按照大小顺序重新排列后,第5、第6个数分别是15和17,所以中位数是(15+17)÷2=16,17出现3次最多,所以众数是17,
故答案为16,17;
(2)14,
答:这10位居民一周内使用共享单车的平均次数是14次;
(3)200×14=2800
答:该小区居民一周内使用共享单车的总次数为2800次.
【点睛】本题考查了中位数、众数、平均数的概念以及利用样本平均数估计总体.抓住概念进行解题,难度不大,但是中位数一定要先将所给数据按照大小顺序重新排列后再求,以免出错.
20.(1)40,25
(2)平均数是1.5,众数是1.5,中位数是1.5
(3)该校每天在校体育活动时间大于的学生有人
【分析】(1)根据每天在校体育活动时间为0.9h的学生人数及所占的百分比可以求得本次调查的学生人数,进而求得m的值;
(2)根据统计图中的数据可以求得这组数据的平均数和众数、中位数;
(3)用800乘以调查的学生中每天在校体育活动时间大于的学生占比即可求得该校每天在校体育活动时间大于的学生人数.
(1)
本次接受调查的初中学生人数为:4÷10%=40,
m%==25%,
故答案为:40,25.
(2)
平均数是:,
众数是,
第20个数和第21个数都是1.5,
∴中位数是1.5;
(3)
(人),
答:该校每天在校体育活动时间大于的学生有人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体、中位数、众数,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(1)50,165和170,170
(2)见解析
(3)185型校服所对应的扇形圆心角的大小为14.4°.
【分析】(1)根据穿165型的人数与所占的百分比列式进行计算即可求出学生总人数,再求总数和中位数;
(2)求出175、185型的人数,然后补全统计图即可;
(3)360°乘以样本中穿185型校服的学生所占比例可得.
(1)
解:该班共有的学生数为15÷30%=50(人),
该班学生所穿校服型号的众数为165和170,中位数为170;
故答案为:50,165和170,170;
(2)
解:175型的人数为50×20%=10(人),
则185型的人数为50-3-15-15-10-5=2(人),
补全条形统计图如下:
(3)
解:360°×=14.4°.
答:185型校服所对应的扇形圆心角的大小为14.4°.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.除此之外,本题也考查了平均数、中位数、众数的认识.
22.(1)13,13,13
(2)甲种小麦苗高不低于13cm的株数有1400株
(3)甲种小麦长势较好
【分析】(1)中位数是将一组数据从小到大(或从大到小重新排列后,最中间的那个数(最中间两个数的平均数);出现次数最多的这个数即为这组数据的众数;
(2)总数量乘以样本中小麦苗高不低于13cm的株数所占比例;
(3)方差越小,数据越稳定,小麦长势较好.
(1)
乙组数据:从小到大排列,6,7,9,11,12,14,16,16,19,20,
排在中间的两个数的平均数为: ,
所以乙组数据的中位数为:13,
即a=13,
甲组数据:13出现的次数最多,所以甲组数据的纵数为:13
即b=13,
乙组数据的平均数为:,
故c=13,
故答案为:13,13,13
(2)
2000×= 1400(株),
答:估计甲种小麦苗高不低于13cm的有1400株;
(3)
因为甲种小麦苗高的方差远小于乙种小麦苗高的方差,故甲种小麦苗高整齐,而两种小麦苗高的中位数和平均数相同,故甲种小麦长势较好.
【点睛】此题主要查了平均数,中位数,方差的意义,平均数表示一组数据的平均程度,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),方差是用来衡量一组数据波动大小的量.
23.(1)8,7.5,8;
(2)七、七、八;
(3)约有300人.
【分析】(1)根据中位数和众数的定义求解即可;
(2)根据中位数、合格率及方差的意义求解即可;
(3)用总人数乘以样本中七、八年级竞赛成绩达到9分及以上人数所占比例即可.
(1)
解:由图表可得:a=,b=,c=8,
故答案为:8,7.5,8;
(2)
从中位数看,七年级中位数大于八年级中位数,
∴七年级高分人数多于八年级,
∴七年级成绩更优异;
从合格率来看,七年级合格率大于八年级,
∴七年级成绩更优异;
从方差来看,八年级成绩的方差小于七年级,
∴八年级的成绩更稳定,即八年级成绩更整齐;
故答案为:七、七、八;
(3)
由题意得:1200×=300(人),
答:估计该校七、八年级共1200名学生中竞赛成绩达到9分及以上的约有300人.
【点睛】本题主要考查众数、中位数的定义,利用中位数、方差做决策以及用样本估计总体,解题的关键是能够从图表中获取有用信息.
24.(1)见解析;(2)甲台阶;(3)见解析
【分析】(1)根据已知条件和示意图可以确定相同点和不同点;
(2)利用方差的定义即可解决问题;
(3)由于要方便游客行走,要重新整修上山的小路,对于这两段台阶路,在台阶数不变的情况下,利用方差的定义即可解决问题.
【详解】(1)由已知数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cmabcdefgh20cm,且 pq),结合示意图,可知:相同点:甲台阶与乙台阶的各阶高度参差不齐,不同点:甲台阶各阶高度的极差比乙台阶小;
(2)甲台阶,因为甲台阶各阶高度的方差比乙台阶小;
(3)使台阶的各阶高度的方差越小越好.
【点睛】本题主要考查了方差在实际生活中的应用,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
一、单选题
1.(2022春·江西南昌·八年级统考期末)从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
2.(2022春·江西上饶·八年级统考期末)某次数学测验中,八(1)班55人平均分为80分,八(2)班45人平均分为70分,则这两个班总平均分为( )
A.75分 B.75.5分 C.76分 D.76.5分
3.(2022春·江西宜春·八年级统考期末)一组数据:的平均数为,众数为,中位数为,则以下判断正确的是( )
A.一定出现在中 B.一定出现在中
C.一定出现在中 D.,,都不会出现在中
4.(2022春·江西赣州·八年级统考期末)为了解某公司员工的年工资情况,小王随机调查了10位员工,某年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20.下列统计量中,能合理反映该公司员工年工资水平的是( )
A.方差 B.众数 C.中位数 D.平均数
5.(2022春·江西宜春·八年级统考期末)根据疫情防控的要求,学校对所有进入校园的师生进行体温检测,其中7名学生的体温(单位)如下:36.6,36.7,36.6,36.4,36.6,36.5,36.7,这组数据的众数和中位数分别是( )
A.36.6,36.4 B.36.6,36.6 C.36.7,36.4 D.36.7,36.6
二、填空题
6.(2022春·江西赣州·八年级统考期末)若一组数据7,6,m,10,9的平均数为8,则m=_____.
7.(2022春·江西新余·八年级统考期末)已知一组数据,,,,的平均数是3,则数据,,,,的平均数是________.
8.(2022春·江西新余·八年级统考期末)现有甲、乙两种糖果的单价与千克数如下表所示.
甲种糖果 乙种糖果
单价(元/千克) 30 20
千克数 2 3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为______元/千克.
9.(2022春·江西宜春·八年级统考期末)南吕是国家历史文化名城,其名源于“昌大南疆,南方昌盛”之意,市内的滕王阁、八一起义纪念馆、海昏侯遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴.某班同学分小组到以上五个地方进行研学,人数分别为:12,5,11,5,7(单位:人),这组数据的中位数是______.
10.(2022春·江西吉安·八年级统考期末)为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况,将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图,根据提供的数据,该班50名同学一周参加体育锻炼时间的中位数是_____,众数是_____.
11.(2022春·江西南昌·八年级统考期末)若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为___________.
12.(2022春·江西赣州·八年级统考期末)已知一个样本1,3,2,2,a,b,c的众数为3,平均数为2,则该样本的方差为___.
13.(2022春·江西上饶·八年级统考期末)甲、乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差s2甲与s2乙的大小关系是s2甲_______s2乙.(填“>”或“<”)
14.(2022春·江西南昌·八年级统考期末)“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则______品种更适合在该村推广.(填“甲”或“乙”)
三、解答题
15.(2022春·江西赣州·八年级统考期末)学校团委组织了一次“中国梦·航天情”系列活动.下面是八年级甲,乙两个班各项目的成绩(单位:分):
项目班次 知识竞赛 演讲比赛 版面创作
甲 85 91 88
乙 90 84 87
(1)如果根据三项成绩的平均分计算最后成绩,请通过计算说明甲、乙两班谁将获胜;
(2)如果将知识竞赛、演讲比赛、版面创作按5:3:2的比例确定最后成绩,请通过计算说明甲乙两班谁将获胜.
16.(2022春·江西赣州·八年级统考期末)为了解学生掌握垃圾分类知识的情况,增强学生环保意识,某学校举行了“垃圾分类人人有责”的知识竞赛活动.现从该校八、九年级中各随机抽取20名学生的竞赛成绩(满分10分,6分及6分以上为合格,8分及8分以上为优秀)进行整理、描述和分析,下面给出了部分信息:
九年级20名学生的竞赛成绩为:3,5,7,6,9,8,6,7,10,9,8,8,6,6,8,8,8,9,9,8.
八、九年级抽取的学生的竞赛成绩统计表
八年级20名学生的竞赛成绩条形统计图
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)该校八、九年级共1600名学生参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
(3)根据以上数据分析,从一个方面评价哪个年级此次竞赛活动成绩更优异.
17.(2022春·江西上饶·八年级统考期末)2021年7月20日,河南郑州遭受特大暴雨袭击,受灾严重,“一方有难,八方支援”,某校全体同学踊跃捐款,支援灾区,为了解捐款情况,随机抽取部分学生的捐款数,并绘制出如图的统计表和统计图,请根据图中情况解答下列问题.
捐款(元) 20 50 100 150 200
人数(人) a 12 10 3 b
(1)本次随机抽取了 名学生的捐款数,表中的a= ,b= ;
(2)本次抽取的这些学生捐款数的众数是 ,中位数是 ,平均数是 ;(结果保留小数点后两位)
(3)若该校共有2000名学生,估计该校学生共捐款多少元?(结果取整数)
18.(2022春·江西宜春·八年级统考期末)某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 2号 3号 4号 5号 总数
甲班 120 118 130 109 123 600
乙班 109 120 115 139 117 600
经统计发现两班总数相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)填空:甲班的优秀率为_________,乙班的优秀率为_________;
(2)填空:甲班比赛数据的中位数为_________,乙班比赛数据的中位数为_________;
(3)根据以上两条信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
19.(2022春·江西上饶·八年级校联考期末)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
20.(2022春·江西赣州·八年级统考期末)“五项管理”、“双减”政策的出台和落实为家校管理、学生减负带来了较好的成效.教育部门为进一步了解“双减”后初中学生每天在校体育活动的时间(单位:),随机调查了某校的部分初中学生.根据调查结果,绘制出如下的统计图和图.请根据相关信息,解答下列问题:
(1)本次接受调查的初中学生人数为______,图中的值为______;
(2)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(3)根据统计的这组每天在校体育活动时间的样本数据,若该校共有名初中学生,估计该校每天在校体育活动时间大于的学生人数.
21.(2022春·江西上饶·八年级统考期末)某校对八(1)班学生所穿校服型号情况进行了调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号).
根据以上信息,解答下列问题:
(1)八(1)班学生共______人,这组数据中的众数是______,中位数是_____;
(2)在条形统计图中,请把空缺部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小,
22.(2022春·江西赣州·八年级统考期末)某实验基地为了考察甲、乙两种小麦的长势,分别从中抽取10株麦苗,测得苗高如下(单位:cm):
甲 12 13 14 13 10 16 13 13 15 11
乙 6 9 7 12 11 16 14 16 20 19
(1)将数据整理,并通过计算后把下表填全:
小麦 中位数 众数 平均数 方差
甲 13 b 13 2.8
乙 a 16 c 21
________,________,________.
(2)若实验基地有甲种小麦2000株,请你估计甲种小麦苗高不低于13cm的株数.
(3)请你选择合适的数据代表,说明哪一种小麦长势较好.
23.(2022春·江西新余·八年级统考期末)每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共1200名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
七年级抽取的学生的竞赛成绩:
4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)根据以上数据分析,从中位数来看,______年级成绩更优异;从合格率来看,______年级成绩更优异;从方差来看,______年级成绩更整齐;
(3)估计该校七、八年级共1200名学生中竞赛成绩达到9分及以上的约有多少人?
24.(2022春·江西上饶·八年级校联考期末)同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图8是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cmabcdefgh20cm,且 pq),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
参考答案:
1.B
【详解】由题意知,a个x1的和为ax1,b个x2的和为bx2,c个x3的和为cx3,数据总共有a+b+c个,所以这个样本的平均数=,故选B.
2.B
【分析】求出各班的总分,再求出其平均数即可.
【详解】解:这两个班总平均分为=75.5(分)
故选B.
【点睛】此题主要考查平均数的求解,解题的关键是熟知加权平均数的计算方法.
3.B
【分析】根据平均数、中位数、众数的定义,对于错误的说法举出反例说明,从而利于排除法求解.
【详解】解:A、如数据0,1,1,4这四个数的平均数是1.5,不是这组数中的某个数,错误,不符合题意;
B、众数是一组数据中出现次数最多的数,它一定是数据中的数,正确,符合题意;
C、如数据1,2,3,4的中位数是2.5,不是这组数中的某个数,错误,不符合题意;
D、众数是一组数据中出现次数最多的数,它一定是数据中的数,错误,不符合题意.
故选:B.
【点睛】本题主要考查了平均数、中位数、众数的定义.平均数等于数据之和除以总个数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
4.C
【分析】根据中位数的定义求解.
【详解】解:中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),反映的是一组数据的中间水平.因此能合理反映该公司年工资中等水平的是中位数.
故选C.
5.B
【分析】这组数据从小到大排列,再根据众数和中位数的概念求解可得.
【详解】解:将这组数据重新排列为36.4,36.5,36.6,36.6,36.6,36.7,36.7,
所以这组数据的众数为36.6,中位数为36.6,
故选:B.
【点睛】本题主要考查众数和中位数,解题的关键是掌握求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
6.8
【分析】根据平均数的定义列出方程,解方程即可求解.
【详解】解:∵一组数据7,6,m,10,9的平均数为8,
∴,
解得.
故答案为:8.
【点睛】本题考查了已知平均数求未知数据的值,掌握平均数的求法是解题的关键.
7.5
【分析】根据平均数的变化规律可得:数据,,,,的平均数是2×3 1.
【详解】解:∵数据x1,x2,x3,x4,x5的平均数是3,
∴数据,,,,的平均数是2×3 1=5,
故答案为:5.
【点睛】本题考查的是算术平均数的求法及运用,熟记平均数的计算公式是解题的关键.
8.24
【分析】根据题意及加权平均数的求法可直接进行求解.
【详解】解:由题意得:
(元/千克);
故答案为24.
【点睛】本题主要考查加权平均数,熟练掌握加权平均数的求法是解题的关键.
9.7
【分析】根据题意,将已知数据从小到大排列,根据中位数的定义即可求解.中位数:把一组数据按从小到大的顺序排列,在中间的一个数字(或者两个数字的平均值)叫做这组数据的中位数.
【详解】将12,5,11,5,7从小到大排列:5,5,7,11,12;
则中位数为.
故答案为:.
【点睛】本题考查了求一组数据的中位数,理解中位数的定义是解题的关键.
10. 9 8.
【分析】根据众数和中位数的定义求解.
【详解】8是出现次数最多的,故众数是8,
这组数据从小到大的顺序排列,处于中间位置的两个数都是9,故中位数是9,
故答案为9;8.
【点睛】本题属于基础题,考查了确定一组数据的中位数和众数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
11.16
【分析】根据已知条件分析,得出x和y中有一个数为21,再根据中位数得出另一个数,从而求出平均数.
【详解】解:∵一组数据21,14,x,y,9的众数和中位数分别是21和15,
若x=y=21,则该组数据的中位数为:21,不符合题意,
则x和y中有一个数为21,另一个数为15,
∴这组数据的平均数为:(9+14+15+21+21)÷5=16,
故答案为:16.
【点睛】本题考查了平均数,中位数,众数的概念,解题的关键是掌握相应的求法.
12.
【详解】因为众数为3,不妨设a=b=3,则1+3+2+2+3+3+c=2×7,所以c=0,
所以方差为.
故答案为.
13.>
【分析】利用方差反映一组数据的波动大小的一个量进行判断.
【详解】解:∵甲地日平均气温的比乙地的日平均气温的变化幅度大,
∴方差s2甲>s2乙.
故答案为>.
【点睛】本题考查了方差:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
14.乙
【分析】由甲,乙的平均数相同,不好比较,但是甲的方差远远大于乙的方差,根据方差的含义分析可得答案.
【详解】解: /亩,﹐/亩,,
从平均数上看,甲,乙相同,但是甲的方差远远大于乙的方差,所以甲品种的稳定性比乙差,
则乙品种更适合在该村推广.
故答案为:乙.
【点睛】本题考查的是利用平均数,方差的含义做决策,掌握平均数与方差的含义是解题的关键.
15.(1)甲班将获胜
(2)乙班将获胜
【分析】(1)根据表格中的数据和平均数的计算方法可以解答本题;
(2)根据加权平均数的计算方法可以解答本题.
(1)
甲班的平均分为:(85 +91 + 88) ÷3= 88(分),
乙班的平均分为:(90 +84+87) + 3= 87(分),
∵88>87,
∴甲班将获胜;
(2)
由题意可得:
甲班的平均分为: (分),
乙班的平均分为:=87.6(分),
∵87.4 < 87.6,
∴乙班将获胜.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
16.(1)7;7.5;85%
(2)880
(3)九年级,理由见解析
【分析】(1)根据题目中的数据和条形统计图中的数据,可以得到a、b、c的值;
(2)先分别求出两个年级成绩优秀的学生人数,再用全校总人数乘以两个年级成绩优秀人数占抽取的两个年级的总人数的比值,即可求解;
(3)从比较众数、中位数,合格率大小可得答案.
【详解】(1)解:由条形图可得,得7分的人数最多,有6人,
所以八年级成绩的众数为7,故a=7,
八年级成绩从小到大排列,第10个与第11个成绩为7分和8分,
所以八年级成绩的中位数是=7.5分,故b=7.5,
八年级成绩6分及6分以上的有1+6+5+4+1=17(人),
所以八年级成绩的合格率为,故c=85%,
故答案为:7;7.5;85%.
(2)解:八年级成绩优秀的人数为:5+4+1=10(人),
九年级成绩优秀的人数为:12人,
1600×=880(人),
答:估计参加此次竞赛活动成绩优秀的学生人数是880人.
(3)解:从众数、中位数,合格率看,都要是九年级大,所以九年级此次竞赛活动成绩更优异.
【点睛】本题考查条形统计图,中位数、众数、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
17.(1)30,3,2
(2)50,75,88.67
(3)估计该校学生共捐款约177340元.
【分析】(1)根据捐款50元的人数和所占的百分比可以求得本次抽查的学生数,进而可以计算出a和b;
(2)根据(1)中补充完整的统计表可以得到本次调查获取的样本数据的众数、中位数和平均数;
(3)根据(2)中的平均数可以计算出该校2000名学生共捐款数.
(1)
解:12÷40%=30(名),
a=30×10%=3(人),
b=30-3-12-10-3=2(人),
故答案为:30,3,2;
(2)
解:由统计表可知,
捐50元的人数12人,人数最多,则众数是50元,
排在第15、16位两个数是50和100,
则中位数是=75(元),
平均数是:88.67(元);
故答案为:50,75,88.67;
(3)
解:2000×88.67=177340(元),
估计该校学生共捐款约177340元.
【点睛】本题考查统计表、扇形统计图、用样本估计总体、中位数、众数和加权平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
18.(1)100%,100%
(2)120,117
(3)将冠军奖状发给甲班,因为甲班5人比赛成绩的优秀率等于乙班,但中位数比乙班大,综合评定甲班比较好
【分析】(1)优秀率就是优秀的人数与总人数的百分比;
(2)中位数就是一组数据中先把所有数据按从大到小或从小到大的顺序排列起来,如果是奇数个时,就是中间的那一个数,如果是偶数个时,就是中间两个数的平均数;
(3)根据计算出来的统计量的意义分析判断.
【详解】(1)解:甲班优秀率为100%,乙班优秀率为100%,
故答案为:100%,100%;
(2)解:甲班5名学生比赛成绩的中位数是120个,乙班5名学生比赛成绩的中位数是117个,
故答案为:120,117;
(3)解:将冠军奖状发给甲班,因为甲班5人比赛成绩的优秀率等于乙班,但中位数比乙班大,综合评定甲班比较好.
【点睛】本题考查统计初步的数据处理能力,涉及优秀率概念、中位数的概念和根据数据分析做决策等知识,熟练掌握相关定义并运用它的意义解决问题是本题关键.
19.(1)16,17;(2)14;(3)2800.
【分析】(1)将数据按照大小顺序重新排列,计算出中间两个数的平均数即是中位数,出现次数最多的即为众数;
(2)根据平均数的概念,将所有数的和除以10即可;
(3)用样本平均数估算总体的平均数.
【详解】(1)按照大小顺序重新排列后,第5、第6个数分别是15和17,所以中位数是(15+17)÷2=16,17出现3次最多,所以众数是17,
故答案为16,17;
(2)14,
答:这10位居民一周内使用共享单车的平均次数是14次;
(3)200×14=2800
答:该小区居民一周内使用共享单车的总次数为2800次.
【点睛】本题考查了中位数、众数、平均数的概念以及利用样本平均数估计总体.抓住概念进行解题,难度不大,但是中位数一定要先将所给数据按照大小顺序重新排列后再求,以免出错.
20.(1)40,25
(2)平均数是1.5,众数是1.5,中位数是1.5
(3)该校每天在校体育活动时间大于的学生有人
【分析】(1)根据每天在校体育活动时间为0.9h的学生人数及所占的百分比可以求得本次调查的学生人数,进而求得m的值;
(2)根据统计图中的数据可以求得这组数据的平均数和众数、中位数;
(3)用800乘以调查的学生中每天在校体育活动时间大于的学生占比即可求得该校每天在校体育活动时间大于的学生人数.
(1)
本次接受调查的初中学生人数为:4÷10%=40,
m%==25%,
故答案为:40,25.
(2)
平均数是:,
众数是,
第20个数和第21个数都是1.5,
∴中位数是1.5;
(3)
(人),
答:该校每天在校体育活动时间大于的学生有人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体、中位数、众数,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(1)50,165和170,170
(2)见解析
(3)185型校服所对应的扇形圆心角的大小为14.4°.
【分析】(1)根据穿165型的人数与所占的百分比列式进行计算即可求出学生总人数,再求总数和中位数;
(2)求出175、185型的人数,然后补全统计图即可;
(3)360°乘以样本中穿185型校服的学生所占比例可得.
(1)
解:该班共有的学生数为15÷30%=50(人),
该班学生所穿校服型号的众数为165和170,中位数为170;
故答案为:50,165和170,170;
(2)
解:175型的人数为50×20%=10(人),
则185型的人数为50-3-15-15-10-5=2(人),
补全条形统计图如下:
(3)
解:360°×=14.4°.
答:185型校服所对应的扇形圆心角的大小为14.4°.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.除此之外,本题也考查了平均数、中位数、众数的认识.
22.(1)13,13,13
(2)甲种小麦苗高不低于13cm的株数有1400株
(3)甲种小麦长势较好
【分析】(1)中位数是将一组数据从小到大(或从大到小重新排列后,最中间的那个数(最中间两个数的平均数);出现次数最多的这个数即为这组数据的众数;
(2)总数量乘以样本中小麦苗高不低于13cm的株数所占比例;
(3)方差越小,数据越稳定,小麦长势较好.
(1)
乙组数据:从小到大排列,6,7,9,11,12,14,16,16,19,20,
排在中间的两个数的平均数为: ,
所以乙组数据的中位数为:13,
即a=13,
甲组数据:13出现的次数最多,所以甲组数据的纵数为:13
即b=13,
乙组数据的平均数为:,
故c=13,
故答案为:13,13,13
(2)
2000×= 1400(株),
答:估计甲种小麦苗高不低于13cm的有1400株;
(3)
因为甲种小麦苗高的方差远小于乙种小麦苗高的方差,故甲种小麦苗高整齐,而两种小麦苗高的中位数和平均数相同,故甲种小麦长势较好.
【点睛】此题主要查了平均数,中位数,方差的意义,平均数表示一组数据的平均程度,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),方差是用来衡量一组数据波动大小的量.
23.(1)8,7.5,8;
(2)七、七、八;
(3)约有300人.
【分析】(1)根据中位数和众数的定义求解即可;
(2)根据中位数、合格率及方差的意义求解即可;
(3)用总人数乘以样本中七、八年级竞赛成绩达到9分及以上人数所占比例即可.
(1)
解:由图表可得:a=,b=,c=8,
故答案为:8,7.5,8;
(2)
从中位数看,七年级中位数大于八年级中位数,
∴七年级高分人数多于八年级,
∴七年级成绩更优异;
从合格率来看,七年级合格率大于八年级,
∴七年级成绩更优异;
从方差来看,八年级成绩的方差小于七年级,
∴八年级的成绩更稳定,即八年级成绩更整齐;
故答案为:七、七、八;
(3)
由题意得:1200×=300(人),
答:估计该校七、八年级共1200名学生中竞赛成绩达到9分及以上的约有300人.
【点睛】本题主要考查众数、中位数的定义,利用中位数、方差做决策以及用样本估计总体,解题的关键是能够从图表中获取有用信息.
24.(1)见解析;(2)甲台阶;(3)见解析
【分析】(1)根据已知条件和示意图可以确定相同点和不同点;
(2)利用方差的定义即可解决问题;
(3)由于要方便游客行走,要重新整修上山的小路,对于这两段台阶路,在台阶数不变的情况下,利用方差的定义即可解决问题.
【详解】(1)由已知数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cmabcdefgh20cm,且 pq),结合示意图,可知:相同点:甲台阶与乙台阶的各阶高度参差不齐,不同点:甲台阶各阶高度的极差比乙台阶小;
(2)甲台阶,因为甲台阶各阶高度的方差比乙台阶小;
(3)使台阶的各阶高度的方差越小越好.
【点睛】本题主要考查了方差在实际生活中的应用,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
