人教A版(2019) 选择性必修 第三册8.3 列联表与独立性检验 课时作业(word版含答案)
文档属性
| 名称 | 人教A版(2019) 选择性必修 第三册8.3 列联表与独立性检验 课时作业(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 384.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 15:32:34 | ||
图片预览



文档简介
8.3 列联表与独立性检验 课时作业
一、单选题
1.两个分类变量和,它们的取值分别为和,其样本频数列联表如下表所示:
合计
合计
则下列四组数据中,分类变量和之间关系最强的是( )
A.,,, B.,,,
C.,,, D.,,,
2.下面是列联表:
合计
21 63
22 35 57
合计 56 120
则表中、的值分别为( )
A.84,60 B.42,64 C.42,74 D.74,42
3.下列说法中正确的是
A.若分类变量和的随机变量的观测值越大,则“与相关”的可信程度越小
B.对于自变量和因变量,当取值一定时,的取值具有一定的随机性,,间的这种非确定关系叫做函数关系
C.相关系数越接近1,表明两个随机变量线性相关性越弱
D.若分类变量与的随机变量的观测值越小,则两个分类变量有关系的把握性越小
4.“绿水青山就是金山银山”,某城市发起了“减少碳排放行动”,通过增加植树面积,逐步实现碳中和,为调查民众对减碳行动的参与情况,在某社区随机调查了90位市民,每位市民对减碳行动给出认可或不认可的评价,得到如图所示的列联表 经计算的观测值,则可以推断出( )
认可 不认可
40岁以下 20 20
40岁以上(含40岁) 40 10
附:
A.该社区居民中约有99%的人认可“减碳行动”
B.该社区居民中约有99.5%的人认可“减碳行动
C.在犯错率不超过0.005的前提下,认为“减碳行动"的认可情况与年龄有关
D.在犯错率不超过0.001的前提下,认为“减碳行动"的认可情况与年龄有关
5.在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,统计成绩后,得到如下2×2列联表:
优秀 非优秀 合计
甲班人数 50
乙班人数 20
合计 30 110
附:,其中.
根据独立性检验,可以认为数学考试成绩与班级有关系的把握为( )
A. B. C. D.
6.现行普通高中学生在高一时面临着选科的问题,学校抽取了部分男 女学生意愿的一份样本,制作出如下两个等高堆积条形图:
根据这两幅图中的信息,下列哪个统计结论是不正确的( )
A.样本中的女生数量多于男生数量
B.样本中有两理一文意愿的学生数量多于有两文一理意愿的学生数量
C.样本中的男生偏爱两理一文
D.样本中的女生偏爱两文一理
二、多选题
7.给出下列命题,其中正确的是( )
A.对于独立性检验的值越大,说明两事件相关程度越大.
B.若随机变量,则
C.若,则
D.已知样本点组成一个样本,得到回归直线方程,且,剔除两个样本点和得到新的回归直线的斜率为,则新的回归方程为
8.以下四个命题中正确的是( )
A.质检员每隔一小时从一条生产流水线上抽取一件产品进行某项指标检测,这样的抽样是系统抽样
B.两个随机变量的线性相关性越强,则相关系数的绝对值越接近于
C.在某项测量中,测量结果服从正态分布(),若在内取值的概率为,则在内取值的概率为
D.对分类变量与的随机变量的观测值来说,越小,判断“与有关系”的把握程度越大
三、填空题
9.某校为了研究学生的性别与对待某一活动的态度(支持和不支持两种态度)的关系,运用列联表进行独立性检验,经计算,则所得到的统计学结论是:有______的把握认为“学生性别与是否支持该活动有关系”.
附:
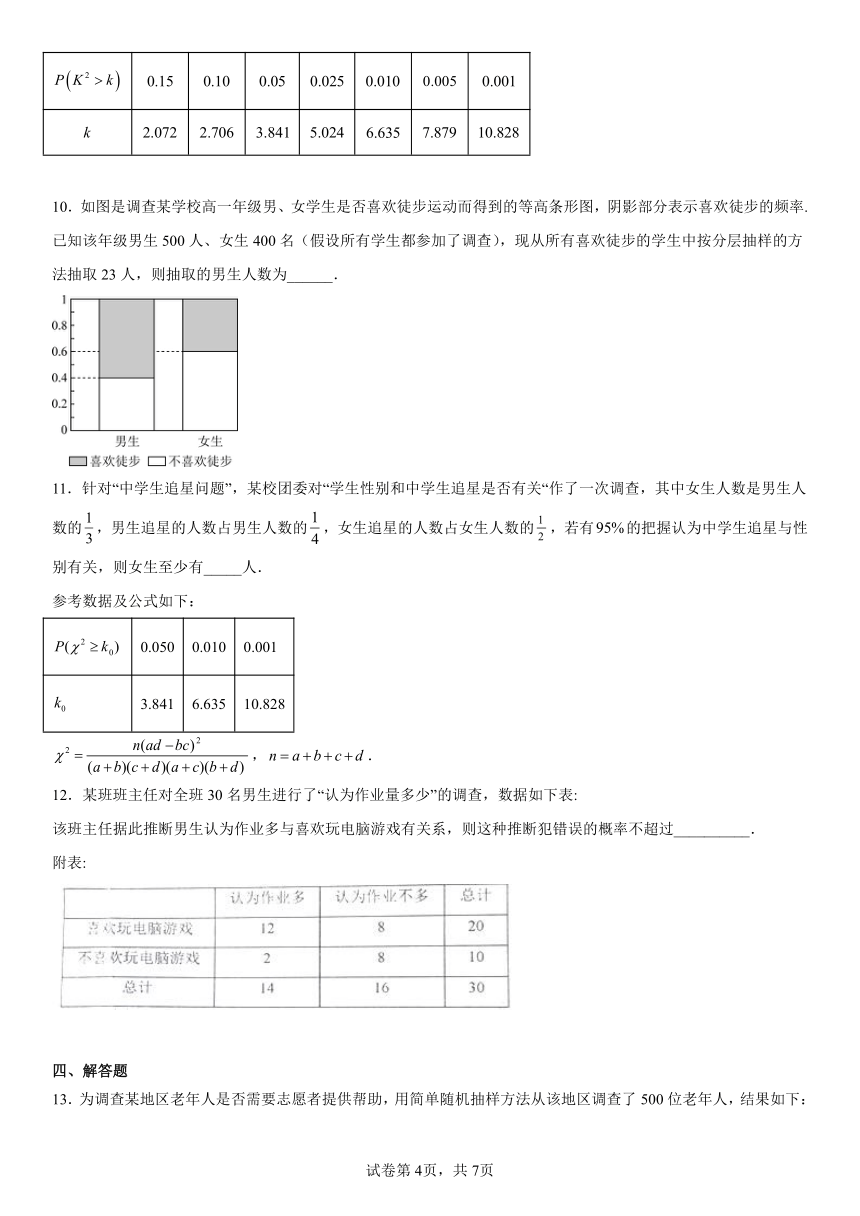
10.如图是调查某学校高一年级男、女学生是否喜欢徒步运动而得到的等高条形图,阴影部分表示喜欢徒步的频率.已知该年级男生500人、女生400名(假设所有学生都参加了调查),现从所有喜欢徒步的学生中按分层抽样的方法抽取23人,则抽取的男生人数为______.
11.针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关“作了一次调查,其中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若有的把握认为中学生追星与性别有关,则女生至少有_____人.
参考数据及公式如下:
0.050 0.010 0.001
3.841 6.635 10.828
,.
12.某班班主任对全班30名男生进行了“认为作业量多少”的调查,数据如下表:
该班主任据此推断男生认为作业多与喜欢玩电脑游戏有关系,则这种推断犯错误的概率不超过__________.
附表:
四、解答题
13.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 女
需要 40 30
不需要 160 270
附:
0.050 0.010 0.001
3.841 6.635 10.828
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99﹪的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
14.为了解国内不同年龄段的民众旅游消费的基本情况.某旅游网站从其数据库中随机抽取了1000条客户信息进行分析,这些客户一年的旅游消费金额数据如下表所示;
旅游消费(千元)
年轻人(人) 95 85 70 50 65 35
中老年人(人) 60 95 115 130 115 85
把一年旅游消费金额满8千元称为“高消费”,否则称为“低消费”.
(1)从这些客户中随机选一人.求该客户是高消费的中老年人的概率;
(2)估计低消费的年轻人的平均消费;(同一组的数据用该组区间的中点值为代表);
(3)完成下面的列联表,并判断能否有99%的把握认为旅游消费的高低与年龄有关.
低消费 高消费 合计
年轻人
中老年人
合计
附表及公式:,其中
0.05 0.010 0.005 0.001
3.841 6.635 7.879 10.828
15.下表为年至年某百货零售企业的线下销售额(单位:万元),其中年份代码年份.
年份代码
线下销售额
(1)已知与具有线性相关关系,求关于的线性回归方程,并预测年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了位男顾客、位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有人、女顾客有人,能否在犯错误的概率不超过的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据:.
16.一则“清华大学要求从 2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实,已有不少高校将游泳列为必修内容.
某中学拟在高一-下学期开设游泳选修课,为了了解高--学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 不喜欢游泳 合计
男生 40
女生 30
合计
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为.
(1).请将上述列联表补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
(2)已知在被调查的学生中有6名来自高一(1) 班,其中4名喜欢游泳,现从这6名学生中随机抽取2人,求恰有1人喜欢游泳的概率.
附:
0.10 0.050 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.D
4.C
5.D
6.D
7.BCD
8.BC
9.99
10.15
11.20
12.0.050.
13.(1);(2)有.
14.(1);(2)(千元);(3)填表见解析;有.
15.(1),万元;(2)能.
16.(1)可以(2)
答案第1页,共2页
答案第1页,共2页
一、单选题
1.两个分类变量和,它们的取值分别为和,其样本频数列联表如下表所示:
合计
合计
则下列四组数据中,分类变量和之间关系最强的是( )
A.,,, B.,,,
C.,,, D.,,,
2.下面是列联表:
合计
21 63
22 35 57
合计 56 120
则表中、的值分别为( )
A.84,60 B.42,64 C.42,74 D.74,42
3.下列说法中正确的是
A.若分类变量和的随机变量的观测值越大,则“与相关”的可信程度越小
B.对于自变量和因变量,当取值一定时,的取值具有一定的随机性,,间的这种非确定关系叫做函数关系
C.相关系数越接近1,表明两个随机变量线性相关性越弱
D.若分类变量与的随机变量的观测值越小,则两个分类变量有关系的把握性越小
4.“绿水青山就是金山银山”,某城市发起了“减少碳排放行动”,通过增加植树面积,逐步实现碳中和,为调查民众对减碳行动的参与情况,在某社区随机调查了90位市民,每位市民对减碳行动给出认可或不认可的评价,得到如图所示的列联表 经计算的观测值,则可以推断出( )
认可 不认可
40岁以下 20 20
40岁以上(含40岁) 40 10
附:
A.该社区居民中约有99%的人认可“减碳行动”
B.该社区居民中约有99.5%的人认可“减碳行动
C.在犯错率不超过0.005的前提下,认为“减碳行动"的认可情况与年龄有关
D.在犯错率不超过0.001的前提下,认为“减碳行动"的认可情况与年龄有关
5.在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,统计成绩后,得到如下2×2列联表:
优秀 非优秀 合计
甲班人数 50
乙班人数 20
合计 30 110
附:,其中.
根据独立性检验,可以认为数学考试成绩与班级有关系的把握为( )
A. B. C. D.
6.现行普通高中学生在高一时面临着选科的问题,学校抽取了部分男 女学生意愿的一份样本,制作出如下两个等高堆积条形图:
根据这两幅图中的信息,下列哪个统计结论是不正确的( )
A.样本中的女生数量多于男生数量
B.样本中有两理一文意愿的学生数量多于有两文一理意愿的学生数量
C.样本中的男生偏爱两理一文
D.样本中的女生偏爱两文一理
二、多选题
7.给出下列命题,其中正确的是( )
A.对于独立性检验的值越大,说明两事件相关程度越大.
B.若随机变量,则
C.若,则
D.已知样本点组成一个样本,得到回归直线方程,且,剔除两个样本点和得到新的回归直线的斜率为,则新的回归方程为
8.以下四个命题中正确的是( )
A.质检员每隔一小时从一条生产流水线上抽取一件产品进行某项指标检测,这样的抽样是系统抽样
B.两个随机变量的线性相关性越强,则相关系数的绝对值越接近于
C.在某项测量中,测量结果服从正态分布(),若在内取值的概率为,则在内取值的概率为
D.对分类变量与的随机变量的观测值来说,越小,判断“与有关系”的把握程度越大
三、填空题
9.某校为了研究学生的性别与对待某一活动的态度(支持和不支持两种态度)的关系,运用列联表进行独立性检验,经计算,则所得到的统计学结论是:有______的把握认为“学生性别与是否支持该活动有关系”.
附:
10.如图是调查某学校高一年级男、女学生是否喜欢徒步运动而得到的等高条形图,阴影部分表示喜欢徒步的频率.已知该年级男生500人、女生400名(假设所有学生都参加了调查),现从所有喜欢徒步的学生中按分层抽样的方法抽取23人,则抽取的男生人数为______.
11.针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关“作了一次调查,其中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若有的把握认为中学生追星与性别有关,则女生至少有_____人.
参考数据及公式如下:
0.050 0.010 0.001
3.841 6.635 10.828
,.
12.某班班主任对全班30名男生进行了“认为作业量多少”的调查,数据如下表:
该班主任据此推断男生认为作业多与喜欢玩电脑游戏有关系,则这种推断犯错误的概率不超过__________.
附表:
四、解答题
13.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 女
需要 40 30
不需要 160 270
附:
0.050 0.010 0.001
3.841 6.635 10.828
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99﹪的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
14.为了解国内不同年龄段的民众旅游消费的基本情况.某旅游网站从其数据库中随机抽取了1000条客户信息进行分析,这些客户一年的旅游消费金额数据如下表所示;
旅游消费(千元)
年轻人(人) 95 85 70 50 65 35
中老年人(人) 60 95 115 130 115 85
把一年旅游消费金额满8千元称为“高消费”,否则称为“低消费”.
(1)从这些客户中随机选一人.求该客户是高消费的中老年人的概率;
(2)估计低消费的年轻人的平均消费;(同一组的数据用该组区间的中点值为代表);
(3)完成下面的列联表,并判断能否有99%的把握认为旅游消费的高低与年龄有关.
低消费 高消费 合计
年轻人
中老年人
合计
附表及公式:,其中
0.05 0.010 0.005 0.001
3.841 6.635 7.879 10.828
15.下表为年至年某百货零售企业的线下销售额(单位:万元),其中年份代码年份.
年份代码
线下销售额
(1)已知与具有线性相关关系,求关于的线性回归方程,并预测年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了位男顾客、位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有人、女顾客有人,能否在犯错误的概率不超过的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据:.
16.一则“清华大学要求从 2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实,已有不少高校将游泳列为必修内容.
某中学拟在高一-下学期开设游泳选修课,为了了解高--学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 不喜欢游泳 合计
男生 40
女生 30
合计
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为.
(1).请将上述列联表补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
(2)已知在被调查的学生中有6名来自高一(1) 班,其中4名喜欢游泳,现从这6名学生中随机抽取2人,求恰有1人喜欢游泳的概率.
附:
0.10 0.050 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.D
4.C
5.D
6.D
7.BCD
8.BC
9.99
10.15
11.20
12.0.050.
13.(1);(2)有.
14.(1);(2)(千元);(3)填表见解析;有.
15.(1),万元;(2)能.
16.(1)可以(2)
答案第1页,共2页
答案第1页,共2页
