2022-2023学年八年级数学下册12.2 二次根式的乘除(课件) 同步精品课堂(苏科版)(共46张PPT)
文档属性
| 名称 | 2022-2023学年八年级数学下册12.2 二次根式的乘除(课件) 同步精品课堂(苏科版)(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 53.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 12:55:22 | ||
图片预览











文档简介
(共46张PPT)
12.2二次根式的乘除
第12章 二次根式
教师
xxx
苏科版 八年级下册
二次根式的乘、除法法则
最简二次根式
二次根式乘除法法则的逆用
二次根式乘除的混合运算
01
03
02
04
CONTANTS
目 录
05
二次根式乘除的应用
二次根式的乘、除法法则
01
学校教学楼后有一长方形花坛(长、宽如图所示,单位:m),现在学校根据需要,想把它改建为草坪.若全部铺满,需购买多少平方米的草皮?
情景引入
比较左右两边的等式,你有什么发现
6
6
20
20
30
30
1.计算下列各式,观察计算结果,你能发现什么规律
(1)
(2)
(3)
新知探究
2.用上题你所发现的规律填空:
=
思考与交流:在前面所发现的规律表达式 · = 中,a,b可否为任意实数?说明理由.
注意:式中a,b
都必须是非负数.
(1) × _____
;
(2) ×=____________.
新知探究
这就是说,两个算术平方根的积,等于它们被开方数的积的算术平方根.
二次根式的乘法法则
注意:被开方数 a,b 既可以是数,也可以是代数式,但都必须是非负的.
新知探究
例1 计算:
解:
提示:
两个二次根式相乘,把被开方数相乘,根指数不变.即:
典型例题
1.思考:你能计算出 ?
解:
是最后的结果吗?还能怎么处理呢?
探究新知
比较左右两边的等式,你有什么发现
计算下列各式,观察计算结果,你能发现什么规律
合作交流
1.独立思考,完成计算;
2.四人一组,讨论规律.
探究新知
计算下列各式:
对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化
观察计算结果,你能发现什么规律
分母不为0
归纳
探究新知
(1) ___÷___=____;
= _____;
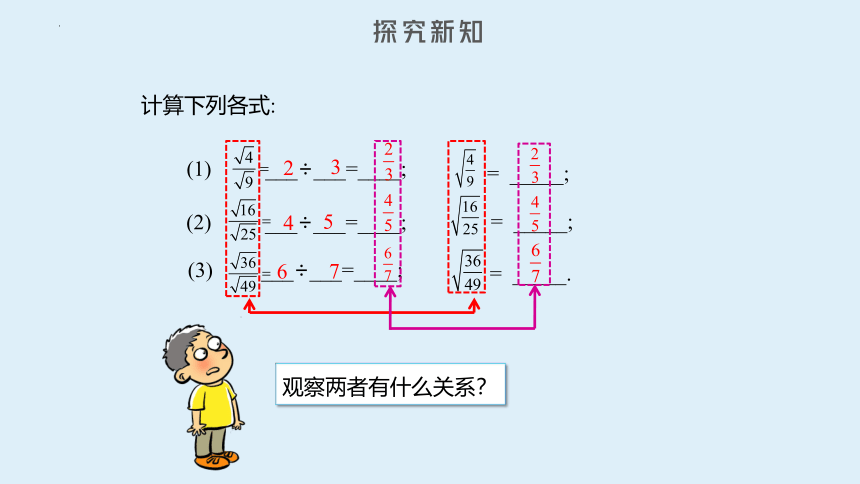
计算下列各式:
(2) ___÷___=____;
(3) ___÷___=____;
= _____;
= _____.
2
3
4
5
6
7
观察两者有什么关系?
探究新知
这就是说,两个算术平方根的商,等于它们被开方数的商的算术平方根.
二次根式的除法法则
探究新知
(2)二次根式的运算结果要尽量化到最简;
(3)如果被开方数是带分数,应先将它化成假分数,以免出现类似
这样的错误;
(4)如果是几个二次根式相除,应按除法法则依次计算,也可以把除法
运算转化为乘法运算来计算.
易错警示:
(1)在 中,特别注意 b>0,若b=0,则无意义;
探究新知
例题2 计算:
典型例题
解:
提示:类似(2)中被开方数中含有带分数,应先将带分数化成
假分数,再运用二次根式除法法则进行运算.
例题3 计算:
(1) ;
(2) .
(1) ;
(2)
典型例题
积与商的算术平方根的性质
02
反过来,根据二次根式的乘法法则可得
我们可以运用它来进行二次根式的解题和化简.
这就是说,积的算术平方根,等于积中各因式的算术平方根的积.
新知探究
例4 化简:
解:
典型例题
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
类似地,把二次根式的除法法则反过来,就得到
商的算术平方根,等于被除式的算术平方根与除式的算术平方根的商.
二次根式的商的算术平方根
探究新知
注意:
(1)商的算术平方根的实质是逆用二次根式的除法.
(2)应用商的算术平方根的前提条件是商中被除式是非负数,
除式是正数.
(3)商的算术平方根的性质的作用是化简二次根式,将分母中
的根号化去.
探究新知
解:
补充解法:
例题5 化简:
(1) ;
(2) ;
(1)
(2)
还有其它解法吗
典型例题
解:
提示:像(5)可以先用商的算术平方根的性质,再运用积的算术平方根性质.
(3) ;
(4) ;
(5) .
(3)
(4)
(5)
典型例题
最简二次根式
03
观察上面各数并思考:
(1)这些数能否再化简? (2)这些数有什么共同特点?
,,
可以发现这些数不能再化简,这些数有两个特点:
(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.
一个二次根式满足什么条件就可以说它是最简二次根式了?
探究新知
提醒:最简二次根式必须满足:
(1)被开方数不含分母,也就是被开方数必须是整数(或整式);
(2)被开方数中每个因数(或因式)的幂的指数都小于2,即每个因数
(或因式)的指数都是1.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
最简二次根式
探究新知
解:(1)
(2)
例题6 将下列各式化为最简二次根式:
(1) (2) (3)
.
(3)
.
典型例题
解:
总结:分母形如 的式子,分子、分母同乘以 可使
分母不含根号.
例题7 化简:
(1) ;
(2) ;
(3) .
(2)
(3)
(1)
典型例题
解:
针对练习
化成最简二次根式的一般方法:
(1)将被开方数中能开得尽方的因数或者因式进行开方,
如 ;
(2)若被开方数中含有带分数,应先将带分数化成假分数,再去分母,并将能开得尽方的因数或者因式进行开方,如
;
(3)若被开方数中含有小数,应先将小数化成分数后再进行化简,如 .
探究新知
二次根式乘除的混合运算
04
二次根式的乘除混合运算
1.进行二次根式的乘除混合运算时,有括号的先算括号内的,没有括号的按
照从左到右的顺序进行.
2.两个二次根式相乘除,根号前的系数对应相乘除,根号内的被开方数对应
相乘除.
探究新知
例题8 计算: .
分析:先把被开方数中的带分数化为假分数,再根据运算法则,按照运算顺
序进行计算.
解:
=
.
探究新知
二次根式的乘除混合运算中的四点注意:
(1)带分数要化成假分数;
(2)要注意确定最后结果的符号;
(3)最后结果一般要化为最简二次根式或整式;
(4)在二次根式的乘除混合运算中,有理数的运算法则同样适用.
探究新知
二次根式乘除法的应用
05
例题9. 一个长方形的长和宽分别是 和2 .求这个长方形的面积.
解:长方形的面积
答:这个长方形的面积为4
典型例题
例题10.高空抛物现象被称为“悬在城市上空的痛”.据报道:一个30g的鸡蛋从18楼抛下来就可以砸破行人的头骨,从25楼抛下可以使人当场死亡.据研究从高空抛物时间t和高度h近似的满足公式 .从100米高空抛物到落地所需时间t2是从50米高空抛物到落地所需时间t1的多少倍?
解:由题意得
探究新知
1.化简 的结果是( )
A.9 B.3 C. D.
B
2.下列根式中,最简二次根式是( )
A. B. C. D.
C
课堂练习
3. 计算:
(1);(2);(3)×().
解:(1).
(2)9.
(3) ×().
课堂练习
4. 计算:
(1);(2);(3).
解:(1).
(2) .
(3).
课堂练习
5.计算:
(1);(2);(3) .
解:(1)
(2).
(3) .
课堂练习
6.计算:
(1) ;(2).
解: (1)
(2).
课堂练习
7.计算:
(1)(2);(3).
分析:可直接利用 计算,也可先将分子化简再计算.
解:(1)方法1: .
方法2:.
(3)
.
解:(2).
1.二次根式的乘、除法法则;
2.二次根式乘除法法则的逆用(积与商的算术平方根的性质);
3.最简二次根式;
4.二次根式乘除的混合运算;
5.二次根式乘除的应用。
课堂小结
感谢观看
12.2二次根式的乘除
第12章 二次根式
教师
xxx
苏科版 八年级下册
二次根式的乘、除法法则
最简二次根式
二次根式乘除法法则的逆用
二次根式乘除的混合运算
01
03
02
04
CONTANTS
目 录
05
二次根式乘除的应用
二次根式的乘、除法法则
01
学校教学楼后有一长方形花坛(长、宽如图所示,单位:m),现在学校根据需要,想把它改建为草坪.若全部铺满,需购买多少平方米的草皮?
情景引入
比较左右两边的等式,你有什么发现
6
6
20
20
30
30
1.计算下列各式,观察计算结果,你能发现什么规律
(1)
(2)
(3)
新知探究
2.用上题你所发现的规律填空:
=
思考与交流:在前面所发现的规律表达式 · = 中,a,b可否为任意实数?说明理由.
注意:式中a,b
都必须是非负数.
(1) × _____
;
(2) ×=____________.
新知探究
这就是说,两个算术平方根的积,等于它们被开方数的积的算术平方根.
二次根式的乘法法则
注意:被开方数 a,b 既可以是数,也可以是代数式,但都必须是非负的.
新知探究
例1 计算:
解:
提示:
两个二次根式相乘,把被开方数相乘,根指数不变.即:
典型例题
1.思考:你能计算出 ?
解:
是最后的结果吗?还能怎么处理呢?
探究新知
比较左右两边的等式,你有什么发现
计算下列各式,观察计算结果,你能发现什么规律
合作交流
1.独立思考,完成计算;
2.四人一组,讨论规律.
探究新知
计算下列各式:
对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化
观察计算结果,你能发现什么规律
分母不为0
归纳
探究新知
(1) ___÷___=____;
= _____;
计算下列各式:
(2) ___÷___=____;
(3) ___÷___=____;
= _____;
= _____.
2
3
4
5
6
7
观察两者有什么关系?
探究新知
这就是说,两个算术平方根的商,等于它们被开方数的商的算术平方根.
二次根式的除法法则
探究新知
(2)二次根式的运算结果要尽量化到最简;
(3)如果被开方数是带分数,应先将它化成假分数,以免出现类似
这样的错误;
(4)如果是几个二次根式相除,应按除法法则依次计算,也可以把除法
运算转化为乘法运算来计算.
易错警示:
(1)在 中,特别注意 b>0,若b=0,则无意义;
探究新知
例题2 计算:
典型例题
解:
提示:类似(2)中被开方数中含有带分数,应先将带分数化成
假分数,再运用二次根式除法法则进行运算.
例题3 计算:
(1) ;
(2) .
(1) ;
(2)
典型例题
积与商的算术平方根的性质
02
反过来,根据二次根式的乘法法则可得
我们可以运用它来进行二次根式的解题和化简.
这就是说,积的算术平方根,等于积中各因式的算术平方根的积.
新知探究
例4 化简:
解:
典型例题
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
类似地,把二次根式的除法法则反过来,就得到
商的算术平方根,等于被除式的算术平方根与除式的算术平方根的商.
二次根式的商的算术平方根
探究新知
注意:
(1)商的算术平方根的实质是逆用二次根式的除法.
(2)应用商的算术平方根的前提条件是商中被除式是非负数,
除式是正数.
(3)商的算术平方根的性质的作用是化简二次根式,将分母中
的根号化去.
探究新知
解:
补充解法:
例题5 化简:
(1) ;
(2) ;
(1)
(2)
还有其它解法吗
典型例题
解:
提示:像(5)可以先用商的算术平方根的性质,再运用积的算术平方根性质.
(3) ;
(4) ;
(5) .
(3)
(4)
(5)
典型例题
最简二次根式
03
观察上面各数并思考:
(1)这些数能否再化简? (2)这些数有什么共同特点?
,,
可以发现这些数不能再化简,这些数有两个特点:
(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.
一个二次根式满足什么条件就可以说它是最简二次根式了?
探究新知
提醒:最简二次根式必须满足:
(1)被开方数不含分母,也就是被开方数必须是整数(或整式);
(2)被开方数中每个因数(或因式)的幂的指数都小于2,即每个因数
(或因式)的指数都是1.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
最简二次根式
探究新知
解:(1)
(2)
例题6 将下列各式化为最简二次根式:
(1) (2) (3)
.
(3)
.
典型例题
解:
总结:分母形如 的式子,分子、分母同乘以 可使
分母不含根号.
例题7 化简:
(1) ;
(2) ;
(3) .
(2)
(3)
(1)
典型例题
解:
针对练习
化成最简二次根式的一般方法:
(1)将被开方数中能开得尽方的因数或者因式进行开方,
如 ;
(2)若被开方数中含有带分数,应先将带分数化成假分数,再去分母,并将能开得尽方的因数或者因式进行开方,如
;
(3)若被开方数中含有小数,应先将小数化成分数后再进行化简,如 .
探究新知
二次根式乘除的混合运算
04
二次根式的乘除混合运算
1.进行二次根式的乘除混合运算时,有括号的先算括号内的,没有括号的按
照从左到右的顺序进行.
2.两个二次根式相乘除,根号前的系数对应相乘除,根号内的被开方数对应
相乘除.
探究新知
例题8 计算: .
分析:先把被开方数中的带分数化为假分数,再根据运算法则,按照运算顺
序进行计算.
解:
=
.
探究新知
二次根式的乘除混合运算中的四点注意:
(1)带分数要化成假分数;
(2)要注意确定最后结果的符号;
(3)最后结果一般要化为最简二次根式或整式;
(4)在二次根式的乘除混合运算中,有理数的运算法则同样适用.
探究新知
二次根式乘除法的应用
05
例题9. 一个长方形的长和宽分别是 和2 .求这个长方形的面积.
解:长方形的面积
答:这个长方形的面积为4
典型例题
例题10.高空抛物现象被称为“悬在城市上空的痛”.据报道:一个30g的鸡蛋从18楼抛下来就可以砸破行人的头骨,从25楼抛下可以使人当场死亡.据研究从高空抛物时间t和高度h近似的满足公式 .从100米高空抛物到落地所需时间t2是从50米高空抛物到落地所需时间t1的多少倍?
解:由题意得
探究新知
1.化简 的结果是( )
A.9 B.3 C. D.
B
2.下列根式中,最简二次根式是( )
A. B. C. D.
C
课堂练习
3. 计算:
(1);(2);(3)×().
解:(1).
(2)9.
(3) ×().
课堂练习
4. 计算:
(1);(2);(3).
解:(1).
(2) .
(3).
课堂练习
5.计算:
(1);(2);(3) .
解:(1)
(2).
(3) .
课堂练习
6.计算:
(1) ;(2).
解: (1)
(2).
课堂练习
7.计算:
(1)(2);(3).
分析:可直接利用 计算,也可先将分子化简再计算.
解:(1)方法1: .
方法2:.
(3)
.
解:(2).
1.二次根式的乘、除法法则;
2.二次根式乘除法法则的逆用(积与商的算术平方根的性质);
3.最简二次根式;
4.二次根式乘除的混合运算;
5.二次根式乘除的应用。
课堂小结
感谢观看
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
