高中数学>人教A版(2019)>选择性必修 第二册>5.1 导数的概念及其意义 课时作业(含答案)
文档属性
| 名称 | 高中数学>人教A版(2019)>选择性必修 第二册>5.1 导数的概念及其意义 课时作业(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 658.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 15:51:31 | ||
图片预览




文档简介
5.1 导数的概念及其意义 课时作业
一、单选题
1.,则等于
A. B. C. D.
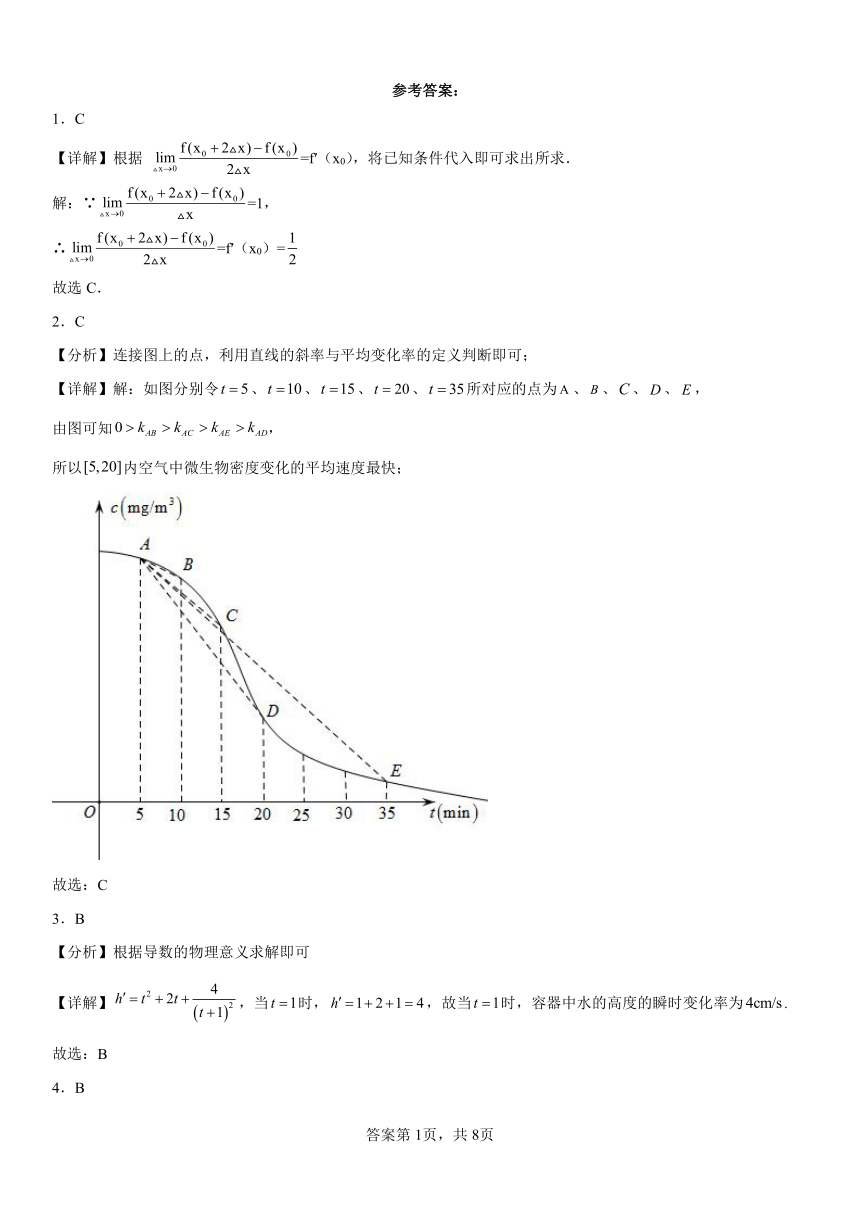
2.降低室内微生物密度的有效方法是定时给室内注入新鲜空气,即开窗通风换气.在某室内,空气中微生物密度(c)随开窗通风换气时间(t)的关系如下图所示.则下列时间段内,空气中微生物密度变化的平均速度最快的是( )
A. B. C. D.
3.向某容器内注入水,已知容器中水的高度h(单位:)与时间t(单位:s)的函数关系式为,则当时,容器中水的高度的瞬时变化率为( )
A. B. C. D.
4.函数的图象如图所示,是函数的导函数,则下列数值排序正确的是( )
A.
B.
C.
D.
5.已知函数,是其导函数,若曲线的一条切线为直线:,且,,不等式恒成立,则实数的取值范围为( )
A. B. C. D.
6.已知函数和在区间上的图象如图所示,则下列说法正确的是( )
A.在a到b之间的平均变化率大于在a到b之间的平均变化率
B.在a到b之间的平均变化率小于在a到b之间的平均变化率
C.对于任意,函数在处的瞬时变化率总大于函数在处的瞬时变化率
D.存在,使得函数在处的瞬时变化率小于函数在处的瞬时变化率
二、多选题
7.已知函数,则下列结论正确的是( )
A.曲线的切线斜率可以是1
B.曲线的切线斜率可以是
C.过点且与曲线相切的直线有且只有1条
D.过点且与曲线相切的直线有且只有2条
8.(多选)下列命题正确的是( )
A.若,则函数在处无切线
B.函数的切线与函数的图象可以有两个公共点
C.曲线在处的切线方程为,则当时,
D.若函数的导数,且,则的图象在处的切线方程为
三、填空题
9.设直线l1,l2分别是函数f(x)=图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则的面积的取值范围是___________
10.已知,则曲线在点处的切线方程是______.
11.已知函数f(x)=aex+x-e的图象在(1,f(1)处的切线过点(e,e),则a的值为_______.
12.若定义在的函数,满足,则曲线在点处的切线方程是___________.
四、解答题
13.已知,求曲线在点处的切线与坐标轴围成的三角形的面积S.
14.已知曲线C1:y=x2与曲线C2:y=-(x-2)2,直线l与C1和C2都相切,求直线l的方程.
15.已知函数在点处的切线方程为.
(1)求函数的解析式;
(2)求函数的单调区间和极值.
16.已知函数,曲线在点,(1)处的切线方程为.
(1)求实数,的值;
(2)若曲线,求曲线过点的切线方程.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】根据 =f′(x0),将已知条件代入即可求出所求.
解:∵=1,
∴=f′(x0)=
故选C.
2.C
【分析】连接图上的点,利用直线的斜率与平均变化率的定义判断即可;
【详解】解:如图分别令、、、、所对应的点为、、、、,
由图可知,
所以内空气中微生物密度变化的平均速度最快;
故选:C
3.B
【分析】根据导数的物理意义求解即可
【详解】,当时,,故当时,容器中水的高度的瞬时变化率为.
故选:B
4.B
【分析】由导数的几何意义判断
【详解】由图象可知在上单调递增
故,即
故选:B
5.C
【分析】通过切线方程求出切点横坐标,令并讨论它的单调性得出;讨论单调性并得,令并讨论其单调性得出,解出的取值范围.
【详解】设切点为,故,而,,故,故,故,因为,故,故,故,故;令,故对任意,,,只需,而,令,解得,故当时,,当时,,故,即;因为在上为减函数,故,则,即;设,易知在上单调递增,所以,所以,故实数的取值范围为,
故选:C.
【点睛】利用导数解决不等式恒成立问题的方法
(1)分离参数法求范围:若或恒成立,只需满足或即可,利用导数方法求出的最小值或的最大值,从而解决问题;
(2)把参数看作常数利用分类讨论方法解决:对于不适合分离参数的不等式,常常将参数看作常数直接构造函数,常用分类讨论法,利用导数研究单调性、最值,从而得出参数范围.
6.D
【解析】由平均变化率和瞬时变化率的概念即可判断.
【详解】解:∵在a到b之间的平均变化率是,
在a到b之间的平均变化率是,
又,,
∴,
∴A、B错误;
易知函数在处的瞬时变化率是函数在处的导数,
即函数在该点处的切线的斜率,
同理可得:函数在处的瞬时变化率是函数在该点处的导数,
即函数在该点处的切线的斜率,
由题中图象可知:
时,函数在处切线的斜率有可能大于在处切线的斜率,也有可能小于在处切线的斜率,故C错误,D正确.
故选:D.
7.AC
【分析】由函数,求导得到,再逐项判断.
【详解】因为函数,所以
A.令,得 ,所以曲线的切线斜率可以是1,故正确;
B.令无解,所以曲线的切线斜率不可以是,故错误;
C. 因为在曲线上,所以点是切点,则,
所以切线方程为,即,所以过点且与曲线相切的直线有且只有1条,故正确;
D.设切点,则切线方程为,因为点在切线上,所以,解得,所以过点且与曲线相切的直线有且只有1条,故错误;
故选:AC
8.BD
【解析】若,则函数在处的切线斜率为0,故选项错误;
可以举例说明函数的切线与函数的图象可以有两个公共点,故选项正确;
,故选项错误;
切线方程为,化简得,故选项正确.
【详解】若,则函数在处的切线斜率为0,故选项错误;
函数的切线与函数的图象可以有两个公共点,例如函数,在处的切线为,与函数的图象还有一个公共点,故选项正确;
因为曲线在处的切线方程为,所以
又,故选项错误;
因为函数的导数,所以,又,所以切点坐标为,斜率为,所以切线方程为,化简得,故选项正确.
故选:BD.
【点睛】易错点睛:很多学生认为曲线的切线与曲线有且只有一个交点,其实曲线的切线可以与曲线有多个交点.
9.(0,1)
【分析】因为,可确定分别在分段函数的两段上,设,且,通过导数可求得切线斜率;根据相互垂直可得到;通过的方程可求得两点坐标,从而得到;联立求得点横坐标,从而将面积表示为,根据可求得面积的取值范围.
【详解】由题意可知,,且明显地,分别在分段函数的两段上
设,且,
,,
,即:
方程为:;方程为:
,,
联立可得点横坐标为:
且在上单调递减,
,即的面积的取值范围为:
故答案为:
【点睛】关键点睛:解题的关键是能够熟练应用导数求解切线斜率,通过垂直关系得到斜率间的关系,进而能够进行化简消元,进而求解的问题;求解取值范围的常用方法是能够将所求三角形面积表示为某一变量的函数,从而利用变量的范围求得面积的取值范围;难度属于困难.
10.
【分析】求得所求切线的斜率为,利用点斜式可求得所求切线的方程.
【详解】,则,,
因此,所求切线的方程为,即.
故答案为:.
【点睛】本题考查利用导数求解函数的切线方程,考查计算能力,属于基础题.
11.
【分析】根据函数的图象在(1,f(1)处的切线过点(e,e),由求解.
【详解】因为函数f(x)=ae+x-e的,
所以,
因为函数的图象在(1,f(1)处的切线过点(e,e),
所以,
解得.
故答案为:.
12.
【分析】根据题意求得的函数,再利用导数的几何意义,即可求解曲线的切线方程.
【详解】由题意,定义在的函数,满足,
可得,
即,
将代入可得,
可得,所以,可得,
又由,所以曲线在点处的切线方程为,
即切线方程为.
故答案为:.
13..
【分析】根据导数的定义可求出,根据导数的几何意义,可得,进而求出切线方程以及切线与两坐标轴的交点坐标,即可求出结果.
【详解】
,
根据导数的概念可得,
,
所以,则,
根据导数的几何意义可得,曲线在点处的切线的斜率,
所以曲线在点处的切线的方程为,即.
令,得;令,得.
由此知该切线与两条坐标轴的交点分别为与,所以所求三角形的面积.
14.或
【分析】先设出直线与两曲线的切点坐标P(x1,)和Q(x2,-(x2-2)2),根据导数的几何意义分别求出切线的方程,再根据两切线重合得到关于和的方程组,求得和后可得切线方程.
【详解】设l与C1相切于点P(x1,),与C2相切于点Q(x2,-(x2-2)2).
对于曲线C1,有y'=2x,
所以与C1相切于点P的切线方程为y-=2x1(x-x1),
即y=2x1x.①
对于曲线C2,有y'=-2(x-2),
所以与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),
即y=-2(x2-2)x+.②
由题意得两切线重合,
所以由①②得,解得或.
所以直线l的方程为或.
【点睛】解答类似问题时,要注意“曲线在点处的切线”和“曲线过点的切线”两种说法的区别,其中“曲线在点处的切线”表明点为切点、且在曲线上,此类问题可直接根据导数的几何意义求解即可.而对于“曲线过点的切线”,则点不一定在曲线上,即使在曲线上,也不一定为切点,该类问题要转化为第一种情况求解.
15.(1);(2)见解析.
【详解】试题分析:(1)根据导数几何意义得,再与联立方程组解得,(2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
试题解析:(1),切线为,即斜率,纵坐标
即,,解得,
解析式
(2) ,定义域为
得到在单增,在单减,在单增
极大值,极小值.
16.(1),;(2)或.
【分析】(1)由已知可得,,列方程求a,b,(2)设设曲线与过点的切线相切于点,,则与直线PA的斜率相等,由此可求切点坐标,并求出对应的切线方程.
【详解】解:(1)的导数为,
由曲线在点,(1)处的切线方程为,
可得,即,
又(1),解得,
即有,;
(2)曲线,即,
导数,
设曲线与过点的切线相切于点,,
则切线的斜率,
所以切线方程为,
即,
因为点在切线上,
所以,
即,
即有,
所以,
解得或,
故所求的切线方程为或.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.,则等于
A. B. C. D.
2.降低室内微生物密度的有效方法是定时给室内注入新鲜空气,即开窗通风换气.在某室内,空气中微生物密度(c)随开窗通风换气时间(t)的关系如下图所示.则下列时间段内,空气中微生物密度变化的平均速度最快的是( )
A. B. C. D.
3.向某容器内注入水,已知容器中水的高度h(单位:)与时间t(单位:s)的函数关系式为,则当时,容器中水的高度的瞬时变化率为( )
A. B. C. D.
4.函数的图象如图所示,是函数的导函数,则下列数值排序正确的是( )
A.
B.
C.
D.
5.已知函数,是其导函数,若曲线的一条切线为直线:,且,,不等式恒成立,则实数的取值范围为( )
A. B. C. D.
6.已知函数和在区间上的图象如图所示,则下列说法正确的是( )
A.在a到b之间的平均变化率大于在a到b之间的平均变化率
B.在a到b之间的平均变化率小于在a到b之间的平均变化率
C.对于任意,函数在处的瞬时变化率总大于函数在处的瞬时变化率
D.存在,使得函数在处的瞬时变化率小于函数在处的瞬时变化率
二、多选题
7.已知函数,则下列结论正确的是( )
A.曲线的切线斜率可以是1
B.曲线的切线斜率可以是
C.过点且与曲线相切的直线有且只有1条
D.过点且与曲线相切的直线有且只有2条
8.(多选)下列命题正确的是( )
A.若,则函数在处无切线
B.函数的切线与函数的图象可以有两个公共点
C.曲线在处的切线方程为,则当时,
D.若函数的导数,且,则的图象在处的切线方程为
三、填空题
9.设直线l1,l2分别是函数f(x)=图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则的面积的取值范围是___________
10.已知,则曲线在点处的切线方程是______.
11.已知函数f(x)=aex+x-e的图象在(1,f(1)处的切线过点(e,e),则a的值为_______.
12.若定义在的函数,满足,则曲线在点处的切线方程是___________.
四、解答题
13.已知,求曲线在点处的切线与坐标轴围成的三角形的面积S.
14.已知曲线C1:y=x2与曲线C2:y=-(x-2)2,直线l与C1和C2都相切,求直线l的方程.
15.已知函数在点处的切线方程为.
(1)求函数的解析式;
(2)求函数的单调区间和极值.
16.已知函数,曲线在点,(1)处的切线方程为.
(1)求实数,的值;
(2)若曲线,求曲线过点的切线方程.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】根据 =f′(x0),将已知条件代入即可求出所求.
解:∵=1,
∴=f′(x0)=
故选C.
2.C
【分析】连接图上的点,利用直线的斜率与平均变化率的定义判断即可;
【详解】解:如图分别令、、、、所对应的点为、、、、,
由图可知,
所以内空气中微生物密度变化的平均速度最快;
故选:C
3.B
【分析】根据导数的物理意义求解即可
【详解】,当时,,故当时,容器中水的高度的瞬时变化率为.
故选:B
4.B
【分析】由导数的几何意义判断
【详解】由图象可知在上单调递增
故,即
故选:B
5.C
【分析】通过切线方程求出切点横坐标,令并讨论它的单调性得出;讨论单调性并得,令并讨论其单调性得出,解出的取值范围.
【详解】设切点为,故,而,,故,故,故,因为,故,故,故,故;令,故对任意,,,只需,而,令,解得,故当时,,当时,,故,即;因为在上为减函数,故,则,即;设,易知在上单调递增,所以,所以,故实数的取值范围为,
故选:C.
【点睛】利用导数解决不等式恒成立问题的方法
(1)分离参数法求范围:若或恒成立,只需满足或即可,利用导数方法求出的最小值或的最大值,从而解决问题;
(2)把参数看作常数利用分类讨论方法解决:对于不适合分离参数的不等式,常常将参数看作常数直接构造函数,常用分类讨论法,利用导数研究单调性、最值,从而得出参数范围.
6.D
【解析】由平均变化率和瞬时变化率的概念即可判断.
【详解】解:∵在a到b之间的平均变化率是,
在a到b之间的平均变化率是,
又,,
∴,
∴A、B错误;
易知函数在处的瞬时变化率是函数在处的导数,
即函数在该点处的切线的斜率,
同理可得:函数在处的瞬时变化率是函数在该点处的导数,
即函数在该点处的切线的斜率,
由题中图象可知:
时,函数在处切线的斜率有可能大于在处切线的斜率,也有可能小于在处切线的斜率,故C错误,D正确.
故选:D.
7.AC
【分析】由函数,求导得到,再逐项判断.
【详解】因为函数,所以
A.令,得 ,所以曲线的切线斜率可以是1,故正确;
B.令无解,所以曲线的切线斜率不可以是,故错误;
C. 因为在曲线上,所以点是切点,则,
所以切线方程为,即,所以过点且与曲线相切的直线有且只有1条,故正确;
D.设切点,则切线方程为,因为点在切线上,所以,解得,所以过点且与曲线相切的直线有且只有1条,故错误;
故选:AC
8.BD
【解析】若,则函数在处的切线斜率为0,故选项错误;
可以举例说明函数的切线与函数的图象可以有两个公共点,故选项正确;
,故选项错误;
切线方程为,化简得,故选项正确.
【详解】若,则函数在处的切线斜率为0,故选项错误;
函数的切线与函数的图象可以有两个公共点,例如函数,在处的切线为,与函数的图象还有一个公共点,故选项正确;
因为曲线在处的切线方程为,所以
又,故选项错误;
因为函数的导数,所以,又,所以切点坐标为,斜率为,所以切线方程为,化简得,故选项正确.
故选:BD.
【点睛】易错点睛:很多学生认为曲线的切线与曲线有且只有一个交点,其实曲线的切线可以与曲线有多个交点.
9.(0,1)
【分析】因为,可确定分别在分段函数的两段上,设,且,通过导数可求得切线斜率;根据相互垂直可得到;通过的方程可求得两点坐标,从而得到;联立求得点横坐标,从而将面积表示为,根据可求得面积的取值范围.
【详解】由题意可知,,且明显地,分别在分段函数的两段上
设,且,
,,
,即:
方程为:;方程为:
,,
联立可得点横坐标为:
且在上单调递减,
,即的面积的取值范围为:
故答案为:
【点睛】关键点睛:解题的关键是能够熟练应用导数求解切线斜率,通过垂直关系得到斜率间的关系,进而能够进行化简消元,进而求解的问题;求解取值范围的常用方法是能够将所求三角形面积表示为某一变量的函数,从而利用变量的范围求得面积的取值范围;难度属于困难.
10.
【分析】求得所求切线的斜率为,利用点斜式可求得所求切线的方程.
【详解】,则,,
因此,所求切线的方程为,即.
故答案为:.
【点睛】本题考查利用导数求解函数的切线方程,考查计算能力,属于基础题.
11.
【分析】根据函数的图象在(1,f(1)处的切线过点(e,e),由求解.
【详解】因为函数f(x)=ae+x-e的,
所以,
因为函数的图象在(1,f(1)处的切线过点(e,e),
所以,
解得.
故答案为:.
12.
【分析】根据题意求得的函数,再利用导数的几何意义,即可求解曲线的切线方程.
【详解】由题意,定义在的函数,满足,
可得,
即,
将代入可得,
可得,所以,可得,
又由,所以曲线在点处的切线方程为,
即切线方程为.
故答案为:.
13..
【分析】根据导数的定义可求出,根据导数的几何意义,可得,进而求出切线方程以及切线与两坐标轴的交点坐标,即可求出结果.
【详解】
,
根据导数的概念可得,
,
所以,则,
根据导数的几何意义可得,曲线在点处的切线的斜率,
所以曲线在点处的切线的方程为,即.
令,得;令,得.
由此知该切线与两条坐标轴的交点分别为与,所以所求三角形的面积.
14.或
【分析】先设出直线与两曲线的切点坐标P(x1,)和Q(x2,-(x2-2)2),根据导数的几何意义分别求出切线的方程,再根据两切线重合得到关于和的方程组,求得和后可得切线方程.
【详解】设l与C1相切于点P(x1,),与C2相切于点Q(x2,-(x2-2)2).
对于曲线C1,有y'=2x,
所以与C1相切于点P的切线方程为y-=2x1(x-x1),
即y=2x1x.①
对于曲线C2,有y'=-2(x-2),
所以与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),
即y=-2(x2-2)x+.②
由题意得两切线重合,
所以由①②得,解得或.
所以直线l的方程为或.
【点睛】解答类似问题时,要注意“曲线在点处的切线”和“曲线过点的切线”两种说法的区别,其中“曲线在点处的切线”表明点为切点、且在曲线上,此类问题可直接根据导数的几何意义求解即可.而对于“曲线过点的切线”,则点不一定在曲线上,即使在曲线上,也不一定为切点,该类问题要转化为第一种情况求解.
15.(1);(2)见解析.
【详解】试题分析:(1)根据导数几何意义得,再与联立方程组解得,(2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
试题解析:(1),切线为,即斜率,纵坐标
即,,解得,
解析式
(2) ,定义域为
得到在单增,在单减,在单增
极大值,极小值.
16.(1),;(2)或.
【分析】(1)由已知可得,,列方程求a,b,(2)设设曲线与过点的切线相切于点,,则与直线PA的斜率相等,由此可求切点坐标,并求出对应的切线方程.
【详解】解:(1)的导数为,
由曲线在点,(1)处的切线方程为,
可得,即,
又(1),解得,
即有,;
(2)曲线,即,
导数,
设曲线与过点的切线相切于点,,
则切线的斜率,
所以切线方程为,
即,
因为点在切线上,
所以,
即,
即有,
所以,
解得或,
故所求的切线方程为或.
答案第1页,共2页
答案第1页,共2页
