18.1.2平行四边形的性质(2) 学案
文档属性
| 名称 | 18.1.2平行四边形的性质(2) 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.1.2平行四边形的性质(2) 导学案
课题 18.1.2平行四边形的性质(2) 单元 第17单元 学科 数学 年级 八年级(下)
教材分析 在掌握平行四边形部分性质的基础上进一步研究平行四边形的其他性质:平行四边形的对角线互相平分.会运用平行四边形的性质解决一些简单的问题,并在应用中探索平行线的性质.
核心素养分析 通过尝试从不同角度寻求解决问题的方法,经历探索平行四边形性质的过程.学会在独立思考的基础上积极参与对数学问题的讨论,享受运用知识解决问题的成功体验.
学习目标 1.理解和掌握平行四边形的对角线互相平分的特征;2.会利用平行四边形的特征进行相关的计算和说明.
重点 理解和掌握平行四边形的对角线互相平分的特征.
难点 会利用平行四边形的特征进行相关的计算和说明.
教学过程
课前预学 引入思考探究一:【活动】请同学们画一个□ABCD,对角线AC和BD相交于O,用刻度尺测量OA,OB,OC,OD的长度,并比较它们的大小关系.再画一个试一试.【答案】OA = , OB = .【结论】平行四边形的对角线 .探究二:在上节课平行四边形的旋转过程中,我们也观察到了OA与OC,OB与OD能够互相重合,请同学们用学过的知识来说明这一现象【回答】 □ABCD是一个 图形,O是它的 ,OA = OC, OB = OD.【总结】由此我们得出了平行四边形的又一个重要特征:平行四边形的对角线互相平分.应用格式:∵ 四边形ABCD是平行四边形,∴ OA = OC,OB = OD(平行四边形的对角线互相平分).【问题提出】你能证明这个定理吗?
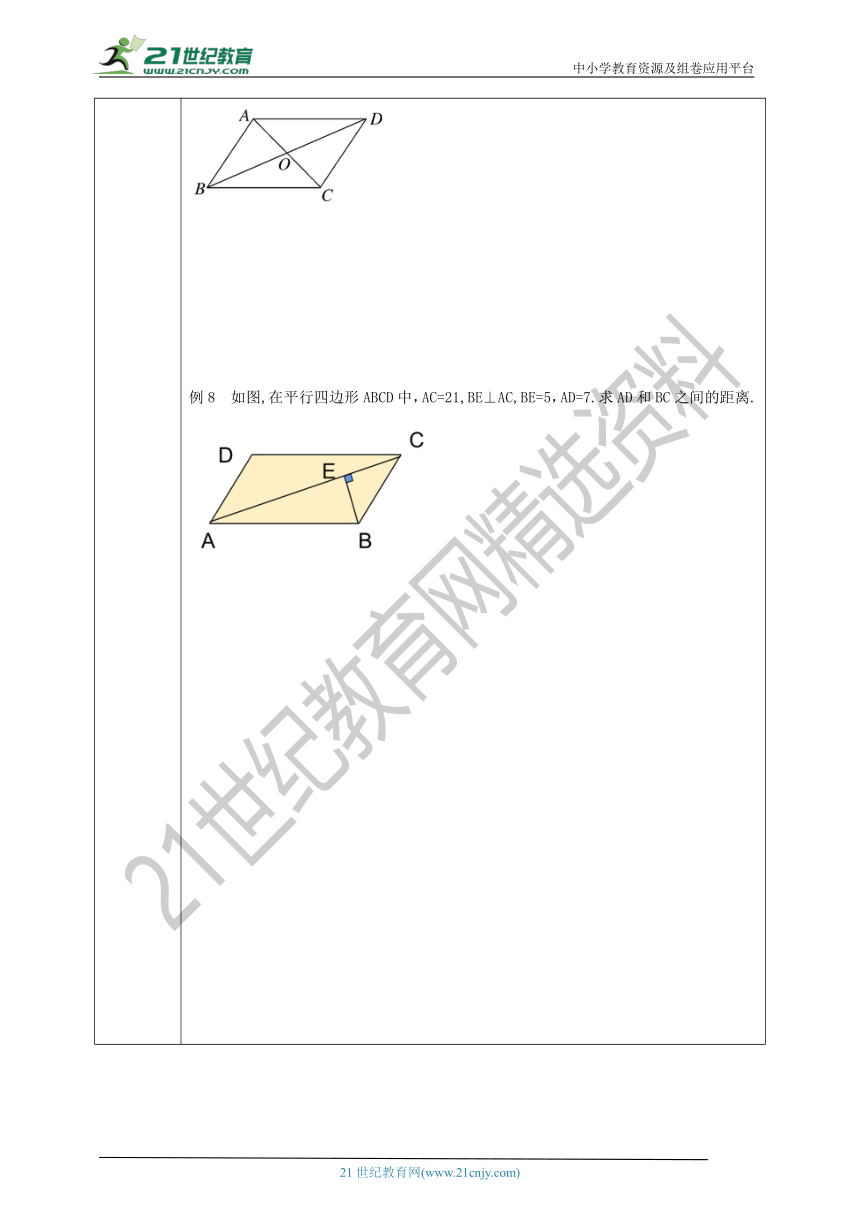
新知讲解 提炼概念在应用平行四边形的性质时,我们应从三个方面去考虑:从边、角、对角线看它们的性质;从“平行四边形的对角线互相平分”中得出“平行四边形被它的两条对角线分成四个小三角形,相邻两个三角形的周长之差等于平行四边形的两邻边之差”;熟记这些结论,能为计算带来很多方便.典例精讲 例5 如图, ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?例6 如图,□ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.例7 如图,平行四边形ABCD的周长为16,三角形AOB的周长比三角形BOC的周长小2.求AB和BC的长.例8 如图,在平行四边形ABCD中,AC=21,BE⊥AC,BE=5,AD=7.求AD和BC之间的距离.
课堂练习 巩固训练1.如图,□ABCD的对角线AC、BD相交于点O,且AC+BD=16,AD=6,则△BOC的周长是( )A、10 B、14C、20 D、222.若平行四边形的对角线长分别为x和y,一边长为12,则x和y的值可能是( )A、8和14 B、10和14 C、18和20 D、10和363.如图,□ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.4.如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF⊥AC,垂足分别为点E、F.求证:OE=OF.5.如图,在□ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F,AB=4,AD=3,OF=1.3.求四边形BCFE的周长.答案引入思考证明:如图,∵ 四边形ABCD是平行四边形, ∴ AB∥CD,AB=CD, ∴ ∠1=∠2,∠3=∠4, ∴ △AOB ≌△COD(ASA), ∴ OA=OC,OB=OD.提炼概念典例精讲 例5 解:在□ ABCD中∵∴AB=6,AO+BO+AB=15,∴AO+BO=15-6=9.又∵AO=OC,BO=OD(平行四边形对角线互相平分),∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18.例6 解:∵ABCD是平行四边形,∴OB=OD(平行四边形对角线互相平分).又∵AB∥CD,∴∠EBO=∠FDO.又∵ ∠EBO=∠DOF,∴△BEO≌△DFO.∴OE=OF.例7 解:∵四边形ABCD是平行四边形,∴OA=OC(平行四边形对角线互相平分).∵ △AOB的周+2= △BOC的周长,∴AO+BO+AB+2=BO+CO+BC,即 AB+2=BC.又∵ □ ABCD的周长=16,∴2(AB+BC)=16,即4AB+4=16.∴AB=3,BC=5.巩固训练1.B2.C3.解:∵四边形ABCD是平行四边形∴AO=OC∵△AOB比△BOC周长小2∴AB+2=BC∵四边形ABCD周长为16,∴AB=3,BC=54.证明:∵平行四边形ABCD的对角线AC、BD交于一点O,∴OD=OB∵BE⊥AC,DF⊥AC∴∠AFD=∠CEB=90°又∵∠DOF=∠BOE∴△ODF≌△OBE∴OF=OE5.解:∵平行四边形ABCD的对角线交于点O, ∴BO=OD,AB//DC ∴∠EBO=∠FDO 又∠EOB=∠FOD ∴△BOE≌△DOF ∴BE=DF ∴四边形BCFE的周长=CD+BC+2OF=9.6
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
18.1.2平行四边形的性质(2) 导学案
课题 18.1.2平行四边形的性质(2) 单元 第17单元 学科 数学 年级 八年级(下)
教材分析 在掌握平行四边形部分性质的基础上进一步研究平行四边形的其他性质:平行四边形的对角线互相平分.会运用平行四边形的性质解决一些简单的问题,并在应用中探索平行线的性质.
核心素养分析 通过尝试从不同角度寻求解决问题的方法,经历探索平行四边形性质的过程.学会在独立思考的基础上积极参与对数学问题的讨论,享受运用知识解决问题的成功体验.
学习目标 1.理解和掌握平行四边形的对角线互相平分的特征;2.会利用平行四边形的特征进行相关的计算和说明.
重点 理解和掌握平行四边形的对角线互相平分的特征.
难点 会利用平行四边形的特征进行相关的计算和说明.
教学过程
课前预学 引入思考探究一:【活动】请同学们画一个□ABCD,对角线AC和BD相交于O,用刻度尺测量OA,OB,OC,OD的长度,并比较它们的大小关系.再画一个试一试.【答案】OA = , OB = .【结论】平行四边形的对角线 .探究二:在上节课平行四边形的旋转过程中,我们也观察到了OA与OC,OB与OD能够互相重合,请同学们用学过的知识来说明这一现象【回答】 □ABCD是一个 图形,O是它的 ,OA = OC, OB = OD.【总结】由此我们得出了平行四边形的又一个重要特征:平行四边形的对角线互相平分.应用格式:∵ 四边形ABCD是平行四边形,∴ OA = OC,OB = OD(平行四边形的对角线互相平分).【问题提出】你能证明这个定理吗?
新知讲解 提炼概念在应用平行四边形的性质时,我们应从三个方面去考虑:从边、角、对角线看它们的性质;从“平行四边形的对角线互相平分”中得出“平行四边形被它的两条对角线分成四个小三角形,相邻两个三角形的周长之差等于平行四边形的两邻边之差”;熟记这些结论,能为计算带来很多方便.典例精讲 例5 如图, ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?例6 如图,□ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.例7 如图,平行四边形ABCD的周长为16,三角形AOB的周长比三角形BOC的周长小2.求AB和BC的长.例8 如图,在平行四边形ABCD中,AC=21,BE⊥AC,BE=5,AD=7.求AD和BC之间的距离.
课堂练习 巩固训练1.如图,□ABCD的对角线AC、BD相交于点O,且AC+BD=16,AD=6,则△BOC的周长是( )A、10 B、14C、20 D、222.若平行四边形的对角线长分别为x和y,一边长为12,则x和y的值可能是( )A、8和14 B、10和14 C、18和20 D、10和363.如图,□ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.4.如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF⊥AC,垂足分别为点E、F.求证:OE=OF.5.如图,在□ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F,AB=4,AD=3,OF=1.3.求四边形BCFE的周长.答案引入思考证明:如图,∵ 四边形ABCD是平行四边形, ∴ AB∥CD,AB=CD, ∴ ∠1=∠2,∠3=∠4, ∴ △AOB ≌△COD(ASA), ∴ OA=OC,OB=OD.提炼概念典例精讲 例5 解:在□ ABCD中∵∴AB=6,AO+BO+AB=15,∴AO+BO=15-6=9.又∵AO=OC,BO=OD(平行四边形对角线互相平分),∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18.例6 解:∵ABCD是平行四边形,∴OB=OD(平行四边形对角线互相平分).又∵AB∥CD,∴∠EBO=∠FDO.又∵ ∠EBO=∠DOF,∴△BEO≌△DFO.∴OE=OF.例7 解:∵四边形ABCD是平行四边形,∴OA=OC(平行四边形对角线互相平分).∵ △AOB的周+2= △BOC的周长,∴AO+BO+AB+2=BO+CO+BC,即 AB+2=BC.又∵ □ ABCD的周长=16,∴2(AB+BC)=16,即4AB+4=16.∴AB=3,BC=5.巩固训练1.B2.C3.解:∵四边形ABCD是平行四边形∴AO=OC∵△AOB比△BOC周长小2∴AB+2=BC∵四边形ABCD周长为16,∴AB=3,BC=54.证明:∵平行四边形ABCD的对角线AC、BD交于一点O,∴OD=OB∵BE⊥AC,DF⊥AC∴∠AFD=∠CEB=90°又∵∠DOF=∠BOE∴△ODF≌△OBE∴OF=OE5.解:∵平行四边形ABCD的对角线交于点O, ∴BO=OD,AB//DC ∴∠EBO=∠FDO 又∠EOB=∠FOD ∴△BOE≌△DOF ∴BE=DF ∴四边形BCFE的周长=CD+BC+2OF=9.6
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
