公倍数和最小公倍数 教案 人教版数学五年级下册
文档属性
| 名称 | 公倍数和最小公倍数 教案 人教版数学五年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 497.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 00:00:00 | ||
图片预览


文档简介
公倍数和最小公倍数
教学目标
1.通过具体操作,领会公倍数和最小公倍数的含义,掌握求两个数公倍数和最小公倍数的方法。
2.经历探究求两个数的公倍数、最小公倍数方法的过程,探寻新旧知识的联系,积累数学活动经验,探索有互质关系和倍数关系的两个数最小公倍数的特点,进一步养成观察、迁移、分析比较和抽象概括的能力。
3.在解决实际问题的过程中,发展数学思考,体验学习和探索活动的乐趣,体会数学源于生活,应用于生活,从而养成热爱数学的情感。
学情分析
该内容是在学生已经学习了“因数和倍数的意义”、 “公因数和最大公因数”等的基础上进行教学的,既是对前面知识的综合运用,同时又是学生学习“通分”所必不可少的知识基础。因而是本单元的教学重点,是本册教材的核心内容。
本课的教学,对于学生的后续学习和发展,具有举足轻重的作用。教材向学生提供了圈数的活动,从中引出公倍数与最小公倍数的概念。在这一活动中,学生不仅知道公倍数与最小公倍数,而且又让学生懂得枚举的方法。因此,在巩固的练习中,应让学生运用所学方法求公倍数和最小公倍数,并鼓励学生主动探索,找到其它的求最小公倍数的方法和总结规律。公倍数和最小公倍数是比较抽象的数学概念,学生要真正理解这些概念仍较为困难。但五年级学生的生活经验和知识背景已经很丰富,而且他们的思维活跃,喜欢挑 战自己,对于新知识总喜欢自己探索,并且喜欢寻找与他人不同的看法。因此,这节课可以放手让学生主动探索,在学生探索的基础上教师作一些适当的指导,这样,可能教学的效果会更好一些。
重点难点
教学重点:经历探究求两个数最小公倍数方法的过程,积累数学活动经验。理解公倍数和最小公倍数的意义。
教学难点:将实际问题转化成找两个数的最小公倍数。
教学过程
一、在游戏中建立公倍数和最小公倍数的概念
1.出示游戏规则
同学们,今天我们请同桌两位同学玩一个跳棋游戏,规则是:
(1)绿棋每次跳3格,黄棋每次跳4格。
(2)为保证公平,绿棋先跳,黄棋后跳,如果两枚棋子跳到同一格,则继续让绿棋先跳。
(3)每次跳完后,在绿棋所跳到的方格画“△”,黄棋所跳到的方格画“○”。先到达终点者胜。
(4)猜拳来决定你选择哪种颜色的棋子。
2.制造矛盾冲突:都来说说组里哪种颜色棋子的同学获胜啦?都是绿棋的同学赢了?现在宣布:绿棋获胜。给绿棋的同学鼓鼓掌。请失败方——黄棋的同学们,你们有什么想说的吗?
预设:不服气,终点是3的倍数,不是4的倍数。所以绿棋赢。
其他黄棋同学的想法呢?是不是像大家说的这样呢?咱们快来一起看一看这个跳棋中还有着怎样的奥秘?你们读一读绿棋每次跳到方格里的数,再读一读黄棋每次跳到方格里的数,看看有新的发现吗?
板书:
绿棋每次跳3格:3、6、9、12、15、18、21、24、27、30
黄棋每次跳4格:4、8、12、16、20、24、28
预设1:绿棋每次跳到方格里的数都是3的倍数
黄棋每次跳到方格里的数都是4的倍数
(教师顺势把板书中“绿棋每次跳3格”改成了“3的倍数”,“黄棋每次跳4格”改成了“4的倍数”)
预设2:绿棋和黄棋相遇是在12、24 (教师顺势将这些数圈起来)
追问:这些数有什么特点呢?(说明什么?)
监控:既是3的倍数,又是4的倍数
4.揭示概念:像这样既是3的倍数,又是4的倍数,是3和4公有的倍数,就可以叫做3和4的公倍数。其中12是最小的就叫做最小公倍数。(板书:公倍数最小公倍数)还可以用中括号的形式表示[3,4] =12(板书:[3,4] =12)。
5.关于公倍数和最小公倍数你有什么想了解的吗?
预设1:怎样求公倍数和最小公倍数?
预设2:特殊关系的两个数的最小公倍数有哪些特点?
预设3:哪些生活中的问题可以用公倍数和最小公倍数来解决?
……
6.小结:就按大家说的我们先来一起研究怎样求两个数的公倍数和最小公倍数。
二、在自主探究中发现找公倍数和最小公倍数的方法
1.提出问题:比如6和8,你能找出它们的公倍数和最小公倍数吗?
2.提出要求:在题纸上独立解决。
3.暴露资源:(预设)
(1)列举法:根据最小公倍数的意义,先找出6的倍数,再找出8的倍数,然后找出6和8的公倍数,最后从中找出最小的一个。
例如:6的倍数:6,12,18,24,30,36,42,48,……
8的倍数:8,16,24,32,40,48,56,……
6和8公倍数:24,48,……6和8的最小公倍数:24
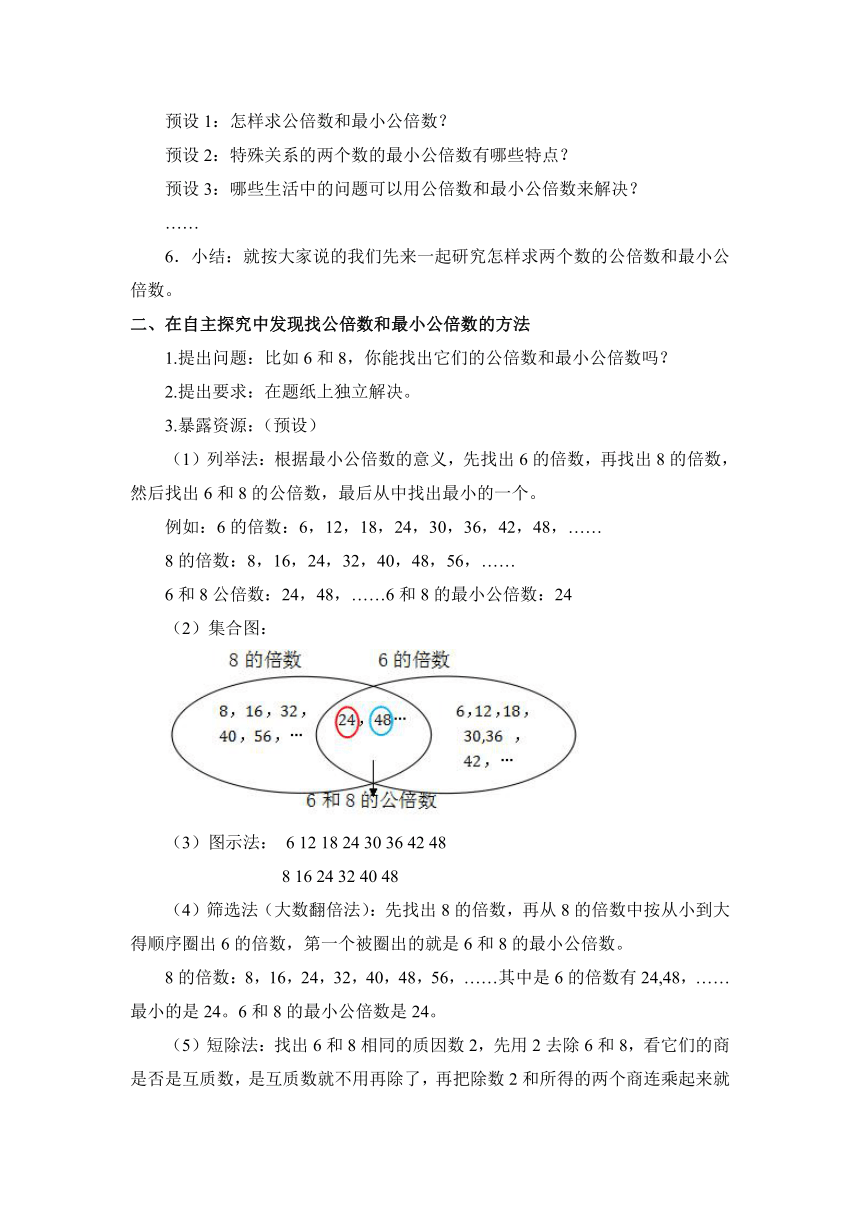
(2)集合图:
(3)图示法: 6 12 18 24 30 36 42 48
8 16 24 32 40 48
(4)筛选法(大数翻倍法):先找出8的倍数,再从8的倍数中按从小到大得顺序圈出6的倍数,第一个被圈出的就是6和8的最小公倍数。
8的倍数:8,16,24,32,40,48,56,……其中是6的倍数有24,48,……最小的是24。6和8的最小公倍数是24。
(5)短除法:找出6和8相同的质因数2,先用2去除6和8,看它们的商是否是互质数,是互质数就不用再除了,再把除数2和所得的两个商连乘起来就是6和8的最小公倍数。
6和8的最小公倍数是2×3×4=24。
(6)分解质因数法:在6和8的公倍数里,应当既包含6的所有质因数,又包含8的所有质因数(两个数相同的质因数取一个),所以6和8的最小公倍数里必须包含它们全部共同的质因数(一个2)以及各自独有的质因数(3和两个2)。
6=2×3
8=2×2×2
6和8的最小公倍数是2×3×2×2=24。
(7)6×8÷2(两个数的乘积除以最大公因数)
4.追问:像第(4)、(5)、(6)、(7)种方法只能求出最小公倍数,不能求公倍数,怎么办?回忆一下我们是怎样通过两个数的最大公因数求出所有公因数的?
预设:看看我们是不是可以找到两个数的公倍数和它们的最小公倍数之间的关系,进而通过最小公倍数求出所有公倍数呢?
5.优化方法。
师:对这几种方法大家有什么看法?
运用列举法先有顺序地排列倍数,再圈一圈的方法是最直观、最容易思考的。当然思路清晰后,再寻求更快的方法就最棒了。
三、在合作交流中发现有特殊关系的两个数的最小公倍数的特点
1.刚才大家还提到要研究特殊关系的两个数的最小公倍数有哪些特点,你们准备研究哪些特殊关系呢?
预设:倍数关系、互质关系
2.谁来说几组倍数关系和互质关系的数,我们一起研究一下?
3.同桌两人合作,选择倍数关系、互质关系各两组进行研究,看看有特殊关系的两个数的最小公倍数有什么特点?
4.总结:两个数是倍数关系,最小公倍数是较大数,最大公因数是较小数。
两个数是互质关系,最小公倍数是两数乘积,最大公因数是1。
四、在解决问题中深化理解公倍数和最小公倍数的概念
我们今天所研究的公倍数和最小公倍数能够帮助我们解决一些实际问题,我们一起来看一下。
(一)解决生活中的问题
1.创设情境、提出问题:
咱们学校社团活动开设了跆拳道班,咱们学校的很多同学都参与了,放假期间,小林和小军也去参加跆拳道训练。小林每6天去一次,小军每9天去一次。7月31日两人同时参加了跆拳道训练,几月几日他们又再次相遇?
2.提出要求:
请大家独立解决。
3.暴露资源:教师搜集学生不同的想法。
4.组织研讨:
(1)6的倍数:6,12,18,24,30
9的倍数:9,18,27
(2)从台历中圈的方法。
刚才老师发现还有同学是这样解决的?可以吗?
5.提升认识:几月几日相遇实际上是找6和9的最小公倍数。将生活问题转化成数学问题。
6.提出问题: 如果是8月5日同时参加训练,下次同时训练又是几月几日呢?
(二)解决生活中的问题
创设情境,提出问题:
咱班同学有没有坐公交车来上学的?下面就是有关公交车的问题,请同学们一起来看一看,你从中获得了哪些数学信息?
提出问题:能解决吗?请同学们自己独立完成
2.提出要求:请大家在练习本上独立解决。
3.暴露资源:教师搜集学生不同的想法。
4.组织研讨:
(1)5的倍数:5,10,15,20,25,30,35,40,45,50,……
8的倍数:8,16,24,32,40,48,56,……
(2)5×8=40
追问:你怎么这么快就做完了?(互质关系)
5.提升认识:至少过多长时间辆车第二次同时发车实际上是找5和8的最小公倍数。
过渡:解决完这几个问题,我们不难发现利用今天所学习的公倍数和最小公倍数可以帮助我们解决生活中的很多实际问题,解决问题的关键是要能够将生活问题转化成数学问题。
五、借助“数学诗”延伸到三个数的最小公倍数
1.出示数学诗
三女探母
三个女儿来看娘,
三五七天各一趟。
今日都往娘家走,
何日一齐再看娘。
2.提出要求:你们自己出声读一读,然后说说这首诗什么意思?
3.你能解决吗?
六、课堂小结
师:同学们,想一想,今天我们学习了什么内容,你有哪些收获?
师:同学们,今天我们从一个游戏中学会了公倍数和最小公倍数的数学知识,并按照大家的思路借助已有的经验,得出了公倍数和最小公倍数的求法,并运用数学知识解决了一些生活中的实际问题,下一节课我们还将运用这部分知识灵活的解决新的问题。
教学目标
1.通过具体操作,领会公倍数和最小公倍数的含义,掌握求两个数公倍数和最小公倍数的方法。
2.经历探究求两个数的公倍数、最小公倍数方法的过程,探寻新旧知识的联系,积累数学活动经验,探索有互质关系和倍数关系的两个数最小公倍数的特点,进一步养成观察、迁移、分析比较和抽象概括的能力。
3.在解决实际问题的过程中,发展数学思考,体验学习和探索活动的乐趣,体会数学源于生活,应用于生活,从而养成热爱数学的情感。
学情分析
该内容是在学生已经学习了“因数和倍数的意义”、 “公因数和最大公因数”等的基础上进行教学的,既是对前面知识的综合运用,同时又是学生学习“通分”所必不可少的知识基础。因而是本单元的教学重点,是本册教材的核心内容。
本课的教学,对于学生的后续学习和发展,具有举足轻重的作用。教材向学生提供了圈数的活动,从中引出公倍数与最小公倍数的概念。在这一活动中,学生不仅知道公倍数与最小公倍数,而且又让学生懂得枚举的方法。因此,在巩固的练习中,应让学生运用所学方法求公倍数和最小公倍数,并鼓励学生主动探索,找到其它的求最小公倍数的方法和总结规律。公倍数和最小公倍数是比较抽象的数学概念,学生要真正理解这些概念仍较为困难。但五年级学生的生活经验和知识背景已经很丰富,而且他们的思维活跃,喜欢挑 战自己,对于新知识总喜欢自己探索,并且喜欢寻找与他人不同的看法。因此,这节课可以放手让学生主动探索,在学生探索的基础上教师作一些适当的指导,这样,可能教学的效果会更好一些。
重点难点
教学重点:经历探究求两个数最小公倍数方法的过程,积累数学活动经验。理解公倍数和最小公倍数的意义。
教学难点:将实际问题转化成找两个数的最小公倍数。
教学过程
一、在游戏中建立公倍数和最小公倍数的概念
1.出示游戏规则
同学们,今天我们请同桌两位同学玩一个跳棋游戏,规则是:
(1)绿棋每次跳3格,黄棋每次跳4格。
(2)为保证公平,绿棋先跳,黄棋后跳,如果两枚棋子跳到同一格,则继续让绿棋先跳。
(3)每次跳完后,在绿棋所跳到的方格画“△”,黄棋所跳到的方格画“○”。先到达终点者胜。
(4)猜拳来决定你选择哪种颜色的棋子。
2.制造矛盾冲突:都来说说组里哪种颜色棋子的同学获胜啦?都是绿棋的同学赢了?现在宣布:绿棋获胜。给绿棋的同学鼓鼓掌。请失败方——黄棋的同学们,你们有什么想说的吗?
预设:不服气,终点是3的倍数,不是4的倍数。所以绿棋赢。
其他黄棋同学的想法呢?是不是像大家说的这样呢?咱们快来一起看一看这个跳棋中还有着怎样的奥秘?你们读一读绿棋每次跳到方格里的数,再读一读黄棋每次跳到方格里的数,看看有新的发现吗?
板书:
绿棋每次跳3格:3、6、9、12、15、18、21、24、27、30
黄棋每次跳4格:4、8、12、16、20、24、28
预设1:绿棋每次跳到方格里的数都是3的倍数
黄棋每次跳到方格里的数都是4的倍数
(教师顺势把板书中“绿棋每次跳3格”改成了“3的倍数”,“黄棋每次跳4格”改成了“4的倍数”)
预设2:绿棋和黄棋相遇是在12、24 (教师顺势将这些数圈起来)
追问:这些数有什么特点呢?(说明什么?)
监控:既是3的倍数,又是4的倍数
4.揭示概念:像这样既是3的倍数,又是4的倍数,是3和4公有的倍数,就可以叫做3和4的公倍数。其中12是最小的就叫做最小公倍数。(板书:公倍数最小公倍数)还可以用中括号的形式表示[3,4] =12(板书:[3,4] =12)。
5.关于公倍数和最小公倍数你有什么想了解的吗?
预设1:怎样求公倍数和最小公倍数?
预设2:特殊关系的两个数的最小公倍数有哪些特点?
预设3:哪些生活中的问题可以用公倍数和最小公倍数来解决?
……
6.小结:就按大家说的我们先来一起研究怎样求两个数的公倍数和最小公倍数。
二、在自主探究中发现找公倍数和最小公倍数的方法
1.提出问题:比如6和8,你能找出它们的公倍数和最小公倍数吗?
2.提出要求:在题纸上独立解决。
3.暴露资源:(预设)
(1)列举法:根据最小公倍数的意义,先找出6的倍数,再找出8的倍数,然后找出6和8的公倍数,最后从中找出最小的一个。
例如:6的倍数:6,12,18,24,30,36,42,48,……
8的倍数:8,16,24,32,40,48,56,……
6和8公倍数:24,48,……6和8的最小公倍数:24
(2)集合图:
(3)图示法: 6 12 18 24 30 36 42 48
8 16 24 32 40 48
(4)筛选法(大数翻倍法):先找出8的倍数,再从8的倍数中按从小到大得顺序圈出6的倍数,第一个被圈出的就是6和8的最小公倍数。
8的倍数:8,16,24,32,40,48,56,……其中是6的倍数有24,48,……最小的是24。6和8的最小公倍数是24。
(5)短除法:找出6和8相同的质因数2,先用2去除6和8,看它们的商是否是互质数,是互质数就不用再除了,再把除数2和所得的两个商连乘起来就是6和8的最小公倍数。
6和8的最小公倍数是2×3×4=24。
(6)分解质因数法:在6和8的公倍数里,应当既包含6的所有质因数,又包含8的所有质因数(两个数相同的质因数取一个),所以6和8的最小公倍数里必须包含它们全部共同的质因数(一个2)以及各自独有的质因数(3和两个2)。
6=2×3
8=2×2×2
6和8的最小公倍数是2×3×2×2=24。
(7)6×8÷2(两个数的乘积除以最大公因数)
4.追问:像第(4)、(5)、(6)、(7)种方法只能求出最小公倍数,不能求公倍数,怎么办?回忆一下我们是怎样通过两个数的最大公因数求出所有公因数的?
预设:看看我们是不是可以找到两个数的公倍数和它们的最小公倍数之间的关系,进而通过最小公倍数求出所有公倍数呢?
5.优化方法。
师:对这几种方法大家有什么看法?
运用列举法先有顺序地排列倍数,再圈一圈的方法是最直观、最容易思考的。当然思路清晰后,再寻求更快的方法就最棒了。
三、在合作交流中发现有特殊关系的两个数的最小公倍数的特点
1.刚才大家还提到要研究特殊关系的两个数的最小公倍数有哪些特点,你们准备研究哪些特殊关系呢?
预设:倍数关系、互质关系
2.谁来说几组倍数关系和互质关系的数,我们一起研究一下?
3.同桌两人合作,选择倍数关系、互质关系各两组进行研究,看看有特殊关系的两个数的最小公倍数有什么特点?
4.总结:两个数是倍数关系,最小公倍数是较大数,最大公因数是较小数。
两个数是互质关系,最小公倍数是两数乘积,最大公因数是1。
四、在解决问题中深化理解公倍数和最小公倍数的概念
我们今天所研究的公倍数和最小公倍数能够帮助我们解决一些实际问题,我们一起来看一下。
(一)解决生活中的问题
1.创设情境、提出问题:
咱们学校社团活动开设了跆拳道班,咱们学校的很多同学都参与了,放假期间,小林和小军也去参加跆拳道训练。小林每6天去一次,小军每9天去一次。7月31日两人同时参加了跆拳道训练,几月几日他们又再次相遇?
2.提出要求:
请大家独立解决。
3.暴露资源:教师搜集学生不同的想法。
4.组织研讨:
(1)6的倍数:6,12,18,24,30
9的倍数:9,18,27
(2)从台历中圈的方法。
刚才老师发现还有同学是这样解决的?可以吗?
5.提升认识:几月几日相遇实际上是找6和9的最小公倍数。将生活问题转化成数学问题。
6.提出问题: 如果是8月5日同时参加训练,下次同时训练又是几月几日呢?
(二)解决生活中的问题
创设情境,提出问题:
咱班同学有没有坐公交车来上学的?下面就是有关公交车的问题,请同学们一起来看一看,你从中获得了哪些数学信息?
提出问题:能解决吗?请同学们自己独立完成
2.提出要求:请大家在练习本上独立解决。
3.暴露资源:教师搜集学生不同的想法。
4.组织研讨:
(1)5的倍数:5,10,15,20,25,30,35,40,45,50,……
8的倍数:8,16,24,32,40,48,56,……
(2)5×8=40
追问:你怎么这么快就做完了?(互质关系)
5.提升认识:至少过多长时间辆车第二次同时发车实际上是找5和8的最小公倍数。
过渡:解决完这几个问题,我们不难发现利用今天所学习的公倍数和最小公倍数可以帮助我们解决生活中的很多实际问题,解决问题的关键是要能够将生活问题转化成数学问题。
五、借助“数学诗”延伸到三个数的最小公倍数
1.出示数学诗
三女探母
三个女儿来看娘,
三五七天各一趟。
今日都往娘家走,
何日一齐再看娘。
2.提出要求:你们自己出声读一读,然后说说这首诗什么意思?
3.你能解决吗?
六、课堂小结
师:同学们,想一想,今天我们学习了什么内容,你有哪些收获?
师:同学们,今天我们从一个游戏中学会了公倍数和最小公倍数的数学知识,并按照大家的思路借助已有的经验,得出了公倍数和最小公倍数的求法,并运用数学知识解决了一些生活中的实际问题,下一节课我们还将运用这部分知识灵活的解决新的问题。
