9.2.4 总体离散程度的估计 课件(共33张PPT)
文档属性
| 名称 | 9.2.4 总体离散程度的估计 课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 40.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 20:03:35 | ||
图片预览










文档简介
(共33张PPT)
9.2.4
总体离散程度的估计
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
统计与概率
TARGET
TARGET
学习目标
01
总体参数
02
分层参数
03
知识应用
04
课堂小结
PART.ONE
PART.01
总体参数
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
总体参数
PART.01
统计
课堂回顾:反应数据总体离散程度的数据有哪些?
思考:若是一组数据平均数和中位数相等,那么该如何利用数据做出有效决策?
总体参数
PART.01
有两位设计运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况做出评价?如果这是一次选拔性考核,你应当如何作出选择?
实例探究
总体参数
PART.01
实例探究
甲的中位数:7 乙的中位数:7
甲的众数:7 乙的众数:7
总体参数
PART.01
实例探究
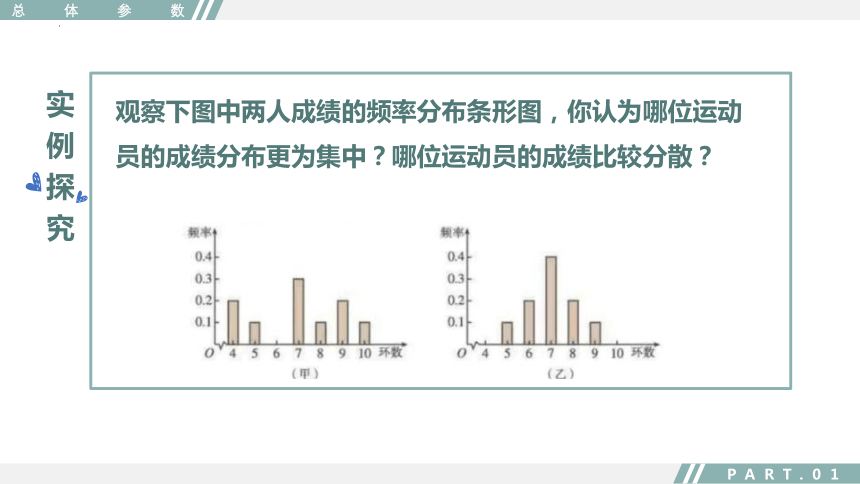
观察下图中两人成绩的频率分布条形图,你认为哪位运动员的成绩分布更为集中?哪位运动员的成绩比较分散?
总体参数
PART.01
实例探究
从下图中可以看出甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定,由此可见甲乙的射击成绩是存在差异的。
总体参数
PART.01
如何度量这一差异
实例探究
极差
甲命中环数的极差=10-4=6
乙命中环数的极差=9-5=4
总体参数
PART.01
用极差刻画数据的离散程度一定准确吗?
实例探究
极差在一定程度上刻画了数据的离散程度.
极差越大,数据的离散程度越大;极差越小,数据的离散程度越小.
但因为极差只使用了数据中最大、最小两个值的信息,对其他数据的取值情况没有涉及,所以极差所含的信息量很少.
总体参数
PART.01
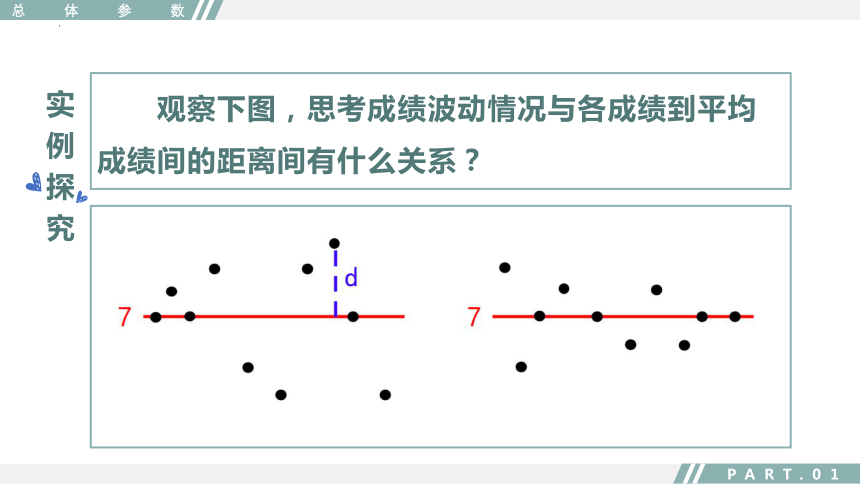
观察下图,思考成绩波动情况与各成绩到平均成绩间的距离间有什么关系?
实例探究
总体参数
PART.01
实例探究
若射击成绩稳定,则大多数射击成绩离平均成绩不会太远;反之则会离平均成绩较远;因此可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度;
如何定义“平均距离”?
总体参数
PART.01
定义探究
假设一组数据是x1,x2,…,xn,用 表示这组数据的平均数.我们用每个数据与平均数的差的绝对值作为“距离”
即:
作为xi到 的“距离”.可以得到这组数据x1,x2,…,xn到 的“平均距离”为
总体参数
PART.01
定义探究
为了避免式中含有绝对值,通常改用平方来代替
方差刻画了数据的离散程度或波动幅度,方差越大,数据的离散程度越大;方差越小,数据的离散程度越小.
总体参数
PART.01
方法归纳
尝试归纳计算方差的基本步骤
①计算平均值
②计算每个数据与平均值的差的平方
③将所有平方相加
④将上述平方和除以数据个数
总体参数
PART.01
深入辨析
能找到更简便的方差计算方法吗?
逐项平方和的平均数
减去平均数的平方
总体参数
PART.01
深入辨析
尝试将方差公式改写成加权的形式
总体参数
PART.01
定义探究
标准差
标准差也可用于衡量一组数据的离散程度或波动情况
标准差越大,数据的波动越大,越不稳定,即离散程度较大;
标准差越小,数据的波动越小,越稳定, 即离散程度较小。
在刻画样本数据的分散程度上,方差和标准差效果是一样的,
但在解决实际问题时,一般多采用标准差。
PART.TWO
PART.02
分层参数
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
分层参数
PART.01
若在身高调查中采用抽样调查,抽取男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62,试根据这些数据,对全体学生的身高作出估计。
实例探究
分层参数
PART.01
解:把男生样本记为x1,x2,…,x23,其平均数记为 方差记为 ;把女生样本记为y1,y2,…,y27,其平均数记为x,方差记为 ;把总样本数据的平均数记为 ,方差记为
实例探究
分层参数
PART.01
根据方差的定义,总样本方差为:
实例探究
由 可得
分层参数
PART.01
因此,
同理可得
实例探究
分层参数
PART.01
由 根据按比例分配分层随机抽样总体样本平均数与各层样本平均数的关系,可得总体样本平均数为
实例探究
分层参数
PART.01
将已知的男生、女生样本平均数和方差的取值带入可得
实例探究
PART.THREE
PART.03
知识应用
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
知识应用
PART.03
在一次射击选拔比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8, 6 ,7,7。
求两位运动员射击成绩的标准差,帮助教练做出选择。
实例探究
知识应用
PART.03
解:
实例探究
知识应用
PART.03
由于 ,但 ,
乙发挥更稳定,故选乙
实例探究
PART.FOUR
PART.04
课堂小结
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
CONCLUSION
PART.04
分享交流你在本堂课中的收获
知识收获
方法收获
思想收获
其他收获
HOMEWORK
PART.04
课后作业
教材213页——练习1,2,3,4,5
END
统计
遨游数海,领略世界
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
9.2.4
总体离散程度的估计
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
统计与概率
TARGET
TARGET
学习目标
01
总体参数
02
分层参数
03
知识应用
04
课堂小结
PART.ONE
PART.01
总体参数
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
总体参数
PART.01
统计
课堂回顾:反应数据总体离散程度的数据有哪些?
思考:若是一组数据平均数和中位数相等,那么该如何利用数据做出有效决策?
总体参数
PART.01
有两位设计运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况做出评价?如果这是一次选拔性考核,你应当如何作出选择?
实例探究
总体参数
PART.01
实例探究
甲的中位数:7 乙的中位数:7
甲的众数:7 乙的众数:7
总体参数
PART.01
实例探究
观察下图中两人成绩的频率分布条形图,你认为哪位运动员的成绩分布更为集中?哪位运动员的成绩比较分散?
总体参数
PART.01
实例探究
从下图中可以看出甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定,由此可见甲乙的射击成绩是存在差异的。
总体参数
PART.01
如何度量这一差异
实例探究
极差
甲命中环数的极差=10-4=6
乙命中环数的极差=9-5=4
总体参数
PART.01
用极差刻画数据的离散程度一定准确吗?
实例探究
极差在一定程度上刻画了数据的离散程度.
极差越大,数据的离散程度越大;极差越小,数据的离散程度越小.
但因为极差只使用了数据中最大、最小两个值的信息,对其他数据的取值情况没有涉及,所以极差所含的信息量很少.
总体参数
PART.01
观察下图,思考成绩波动情况与各成绩到平均成绩间的距离间有什么关系?
实例探究
总体参数
PART.01
实例探究
若射击成绩稳定,则大多数射击成绩离平均成绩不会太远;反之则会离平均成绩较远;因此可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度;
如何定义“平均距离”?
总体参数
PART.01
定义探究
假设一组数据是x1,x2,…,xn,用 表示这组数据的平均数.我们用每个数据与平均数的差的绝对值作为“距离”
即:
作为xi到 的“距离”.可以得到这组数据x1,x2,…,xn到 的“平均距离”为
总体参数
PART.01
定义探究
为了避免式中含有绝对值,通常改用平方来代替
方差刻画了数据的离散程度或波动幅度,方差越大,数据的离散程度越大;方差越小,数据的离散程度越小.
总体参数
PART.01
方法归纳
尝试归纳计算方差的基本步骤
①计算平均值
②计算每个数据与平均值的差的平方
③将所有平方相加
④将上述平方和除以数据个数
总体参数
PART.01
深入辨析
能找到更简便的方差计算方法吗?
逐项平方和的平均数
减去平均数的平方
总体参数
PART.01
深入辨析
尝试将方差公式改写成加权的形式
总体参数
PART.01
定义探究
标准差
标准差也可用于衡量一组数据的离散程度或波动情况
标准差越大,数据的波动越大,越不稳定,即离散程度较大;
标准差越小,数据的波动越小,越稳定, 即离散程度较小。
在刻画样本数据的分散程度上,方差和标准差效果是一样的,
但在解决实际问题时,一般多采用标准差。
PART.TWO
PART.02
分层参数
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
分层参数
PART.01
若在身高调查中采用抽样调查,抽取男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62,试根据这些数据,对全体学生的身高作出估计。
实例探究
分层参数
PART.01
解:把男生样本记为x1,x2,…,x23,其平均数记为 方差记为 ;把女生样本记为y1,y2,…,y27,其平均数记为x,方差记为 ;把总样本数据的平均数记为 ,方差记为
实例探究
分层参数
PART.01
根据方差的定义,总样本方差为:
实例探究
由 可得
分层参数
PART.01
因此,
同理可得
实例探究
分层参数
PART.01
由 根据按比例分配分层随机抽样总体样本平均数与各层样本平均数的关系,可得总体样本平均数为
实例探究
分层参数
PART.01
将已知的男生、女生样本平均数和方差的取值带入可得
实例探究
PART.THREE
PART.03
知识应用
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
知识应用
PART.03
在一次射击选拔比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8, 6 ,7,7。
求两位运动员射击成绩的标准差,帮助教练做出选择。
实例探究
知识应用
PART.03
解:
实例探究
知识应用
PART.03
由于 ,但 ,
乙发挥更稳定,故选乙
实例探究
PART.FOUR
PART.04
课堂小结
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
CONCLUSION
PART.04
分享交流你在本堂课中的收获
知识收获
方法收获
思想收获
其他收获
HOMEWORK
PART.04
课后作业
教材213页——练习1,2,3,4,5
END
统计
遨游数海,领略世界
统计学:通过收集数据和分析数据来认识未知现象的一门科学。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
