2022—2023学年人教版数学八年级下册18.2 特殊的平行四边形(巩固练习)(无答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册18.2 特殊的平行四边形(巩固练习)(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 00:00:00 | ||
图片预览


文档简介
18.2 特殊的平行四边形(巩固练习)-人教版八年级下册
一.选择题
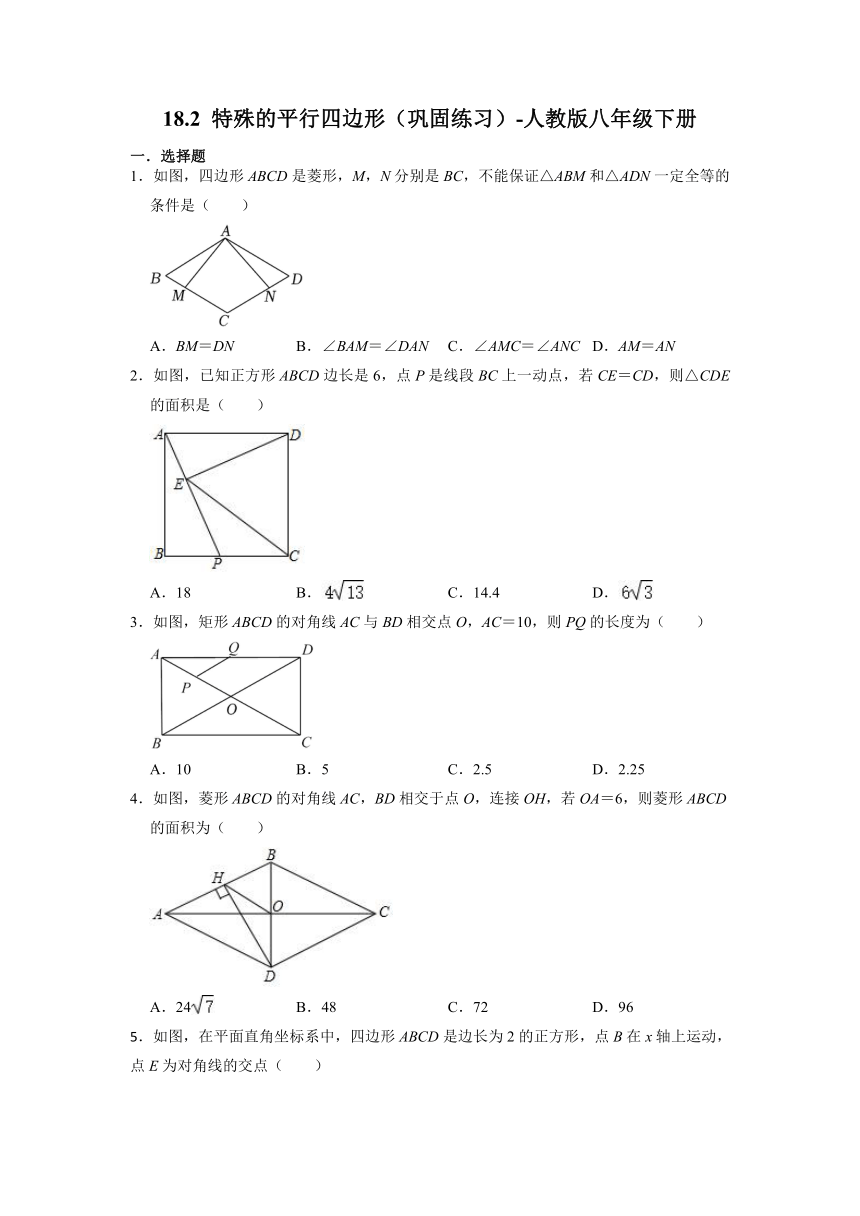
1.如图,四边形ABCD是菱形,M,N分别是BC,不能保证△ABM和△ADN一定全等的条件是( )
A.BM=DN B.∠BAM=∠DAN C.∠AMC=∠ANC D.AM=AN
2.如图,已知正方形ABCD边长是6,点P是线段BC上一动点,若CE=CD,则△CDE的面积是( )
A.18 B. C.14.4 D.
3.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,则PQ的长度为( )
A.10 B.5 C.2.5 D.2.25
4.如图,菱形ABCD的对角线AC,BD相交于点O,连接OH,若OA=6,则菱形ABCD的面积为( )
A.24 B.48 C.72 D.96
.如图,在平面直角坐标系中,四边形ABCD是边长为2的正方形,点B在x轴上运动,点E为对角线的交点( )
A. B.1 C. D.2
.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
.下列结论中,菱形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对边相等且平行
.小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,并测得∠ABC=90°,若图2对角线BD=40cm( )
A.20cm B.20cm C.20cm D.20cm
.已知四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是( )
A.AC⊥BD B.∠ABC=90°
C.AC与BD互相平分 D.AB=BC
.在矩形(长方形)ABCD中,AB=3,若在矩形内找一点P,使△PAB,△PCD,△PAD都为等腰三角形( )个.
A.3 个 B.4 个 C.5 个 D.6 个
二.填空题
.在菱形ABCD中,∠B=60°,AB=8,CE=4,若点P是菱形ABCD四条边上异于点E的一点,则DP的长为 .
.如图所示,已知正方形ABCD的面积为100,菱形PQCB的面积为60 .
.如图,四边形ABCD为菱形,∠ABC=70°,在∠DCE内作射线CM,使得∠ECM=15°过点D作DF⊥CM,若DF=,则对角线BD的长为 .
.如图,E,F分别是边长为4的正方形ABCD的边AD,DC上的动点,连接AF,BE,连接DP,则DP的最小值是 .
.在综合实践课上,小明把边长为2cm,∠B=120°的菱形纸片沿着对角线AC剪开如图1所示,把纸片△ADC沿AC的方向平移得到△A′D′C′,连A′B,D′C,如图2所示
(1)当点A′平移至AC中点时,则CD′= .
(2)若A′B⊥BC时,则四边形A′BCD′的面积为 .
三.解答题
.如图,在正方形ABCD中,E是边AB的中点,连接CE、DF.求证:CE=DF.
.如图,在△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于F,求证:四边形ADCF是菱形.
.已知平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F.
(1)如图1,求证:四边形AECF为矩形.
(2)如图2,连接BF、DE分别交AE、CF于M、N两点,请直接写出图中的所有平行四边形.
.如图, ABCD中,AB=2cm,S ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,点F从D点出发,以同样的速度在CD延长线上向左运动
(1)在运动过程中,四边形AECF的形状是 ;
(2)t= 时,四边形AECF是矩形;
(3)求当t等于多少时,四边形AECF是菱形.
.如图,已知△ABC中,D是BC边上一点,作DF∥AB交AC于点F,连接AD.
(1)下列条件:
①D是BC边的中点;
②AD是△ABC的角平分线;
③点E与点F关于直线AD对称.
请从中选择一个能证明四边形AEDF是菱形的条件,并写出证明过程;
(2)若四边形AEDF是菱形,且AE=2,CF=1
一.选择题
1.如图,四边形ABCD是菱形,M,N分别是BC,不能保证△ABM和△ADN一定全等的条件是( )
A.BM=DN B.∠BAM=∠DAN C.∠AMC=∠ANC D.AM=AN
2.如图,已知正方形ABCD边长是6,点P是线段BC上一动点,若CE=CD,则△CDE的面积是( )
A.18 B. C.14.4 D.
3.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,则PQ的长度为( )
A.10 B.5 C.2.5 D.2.25
4.如图,菱形ABCD的对角线AC,BD相交于点O,连接OH,若OA=6,则菱形ABCD的面积为( )
A.24 B.48 C.72 D.96
.如图,在平面直角坐标系中,四边形ABCD是边长为2的正方形,点B在x轴上运动,点E为对角线的交点( )
A. B.1 C. D.2
.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )
A.∠ABC=90° B.AC=BD C.AD=AB D.∠BAD=∠ADC
.下列结论中,菱形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对边相等且平行
.小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,并测得∠ABC=90°,若图2对角线BD=40cm( )
A.20cm B.20cm C.20cm D.20cm
.已知四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是( )
A.AC⊥BD B.∠ABC=90°
C.AC与BD互相平分 D.AB=BC
.在矩形(长方形)ABCD中,AB=3,若在矩形内找一点P,使△PAB,△PCD,△PAD都为等腰三角形( )个.
A.3 个 B.4 个 C.5 个 D.6 个
二.填空题
.在菱形ABCD中,∠B=60°,AB=8,CE=4,若点P是菱形ABCD四条边上异于点E的一点,则DP的长为 .
.如图所示,已知正方形ABCD的面积为100,菱形PQCB的面积为60 .
.如图,四边形ABCD为菱形,∠ABC=70°,在∠DCE内作射线CM,使得∠ECM=15°过点D作DF⊥CM,若DF=,则对角线BD的长为 .
.如图,E,F分别是边长为4的正方形ABCD的边AD,DC上的动点,连接AF,BE,连接DP,则DP的最小值是 .
.在综合实践课上,小明把边长为2cm,∠B=120°的菱形纸片沿着对角线AC剪开如图1所示,把纸片△ADC沿AC的方向平移得到△A′D′C′,连A′B,D′C,如图2所示
(1)当点A′平移至AC中点时,则CD′= .
(2)若A′B⊥BC时,则四边形A′BCD′的面积为 .
三.解答题
.如图,在正方形ABCD中,E是边AB的中点,连接CE、DF.求证:CE=DF.
.如图,在△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于F,求证:四边形ADCF是菱形.
.已知平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F.
(1)如图1,求证:四边形AECF为矩形.
(2)如图2,连接BF、DE分别交AE、CF于M、N两点,请直接写出图中的所有平行四边形.
.如图, ABCD中,AB=2cm,S ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,点F从D点出发,以同样的速度在CD延长线上向左运动
(1)在运动过程中,四边形AECF的形状是 ;
(2)t= 时,四边形AECF是矩形;
(3)求当t等于多少时,四边形AECF是菱形.
.如图,已知△ABC中,D是BC边上一点,作DF∥AB交AC于点F,连接AD.
(1)下列条件:
①D是BC边的中点;
②AD是△ABC的角平分线;
③点E与点F关于直线AD对称.
请从中选择一个能证明四边形AEDF是菱形的条件,并写出证明过程;
(2)若四边形AEDF是菱形,且AE=2,CF=1
