18.2.1矩形 巩固培优练习(含答案)2022-2023学年人教版数学八年级下册
文档属性
| 名称 | 18.2.1矩形 巩固培优练习(含答案)2022-2023学年人教版数学八年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 694.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 15:41:17 | ||
图片预览

文档简介
18.2.1矩形 巩固培优练习
一、单选题
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AC=10,则图中长度为5的线段共有( )
A.2条 B.4条 C.5条 D.6条
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
3.若顺次连接某四边形的四边中点得到一个矩形,则原四边形一定是( )
A.任意四边形 B.对角线相等的四边形 C.平行四边形 D.对角线互相垂直的四边形
4.如图,在矩形中,,相交于点,若的面积是,则矩形的面积是( )
A. B. C. D.
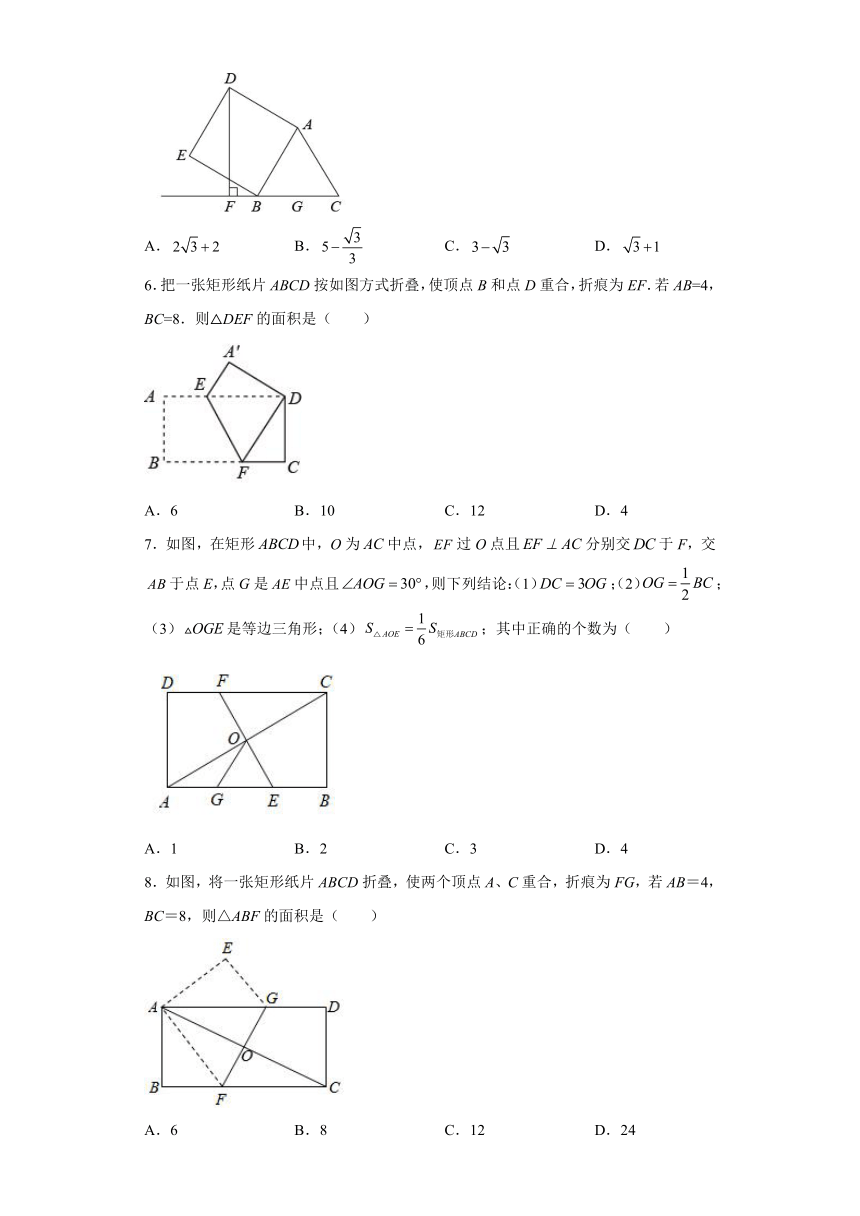
5.如图,在边长为2的等边三角形的外侧作正方形,过点作,垂足为,则的长为( )
A. B. C. D.
6.把一张矩形纸片ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4,BC=8.则△DEF的面积是( )
A.6 B.10 C.12 D.4
7.如图,在矩形中,O为中点,过O点且分别交于F,交于点E,点G是中点且,则下列结论:(1);(2);(3)是等边三角形;(4);其中正确的个数为( )
A.1 B.2 C.3 D.4
8.如图,将一张矩形纸片ABCD折叠,使两个顶点A、C重合,折痕为FG,若AB=4,BC=8,则△ABF的面积是( )
A.6 B.8 C.12 D.24
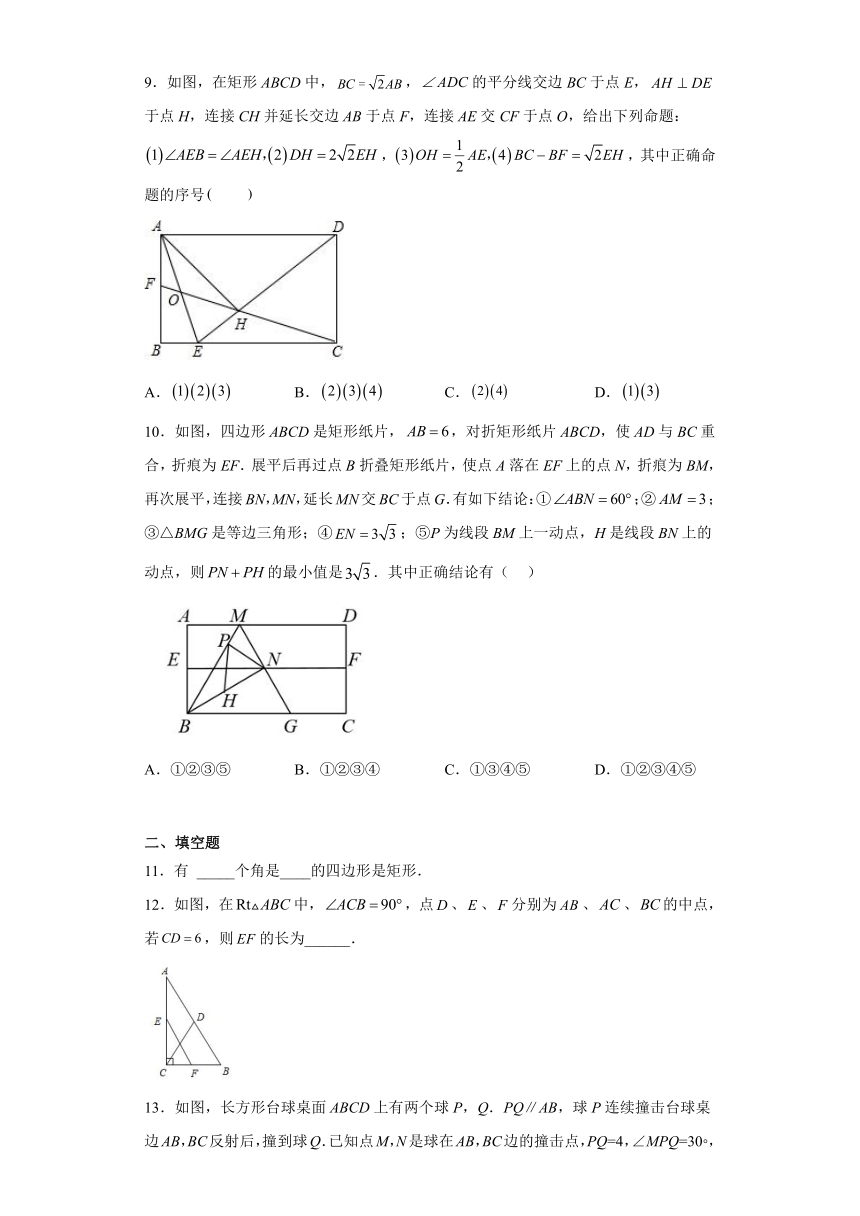
9.如图,在矩形ABCD中,,的平分线交边BC于点E,于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:,,其中正确命题的序号
A. B. C. D.
10.如图,四边形ABCD是矩形纸片,,对折矩形纸片ABCD,使AD与BC重合,折痕为EF.展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕为BM,再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①;②;③△BMG是等边三角形;④;⑤P为线段BM上一动点,H是线段BN上的动点,则的最小值是.其中正确结论有( )
A.①②③⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
二、填空题
11.有 _____个角是____的四边形是矩形.
12.如图,在中,,点、、分别为、、的中点,若,则的长为______.
13.如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30 ,且点P到AB边的距离为3,则四边形PMNQ的周长为__.
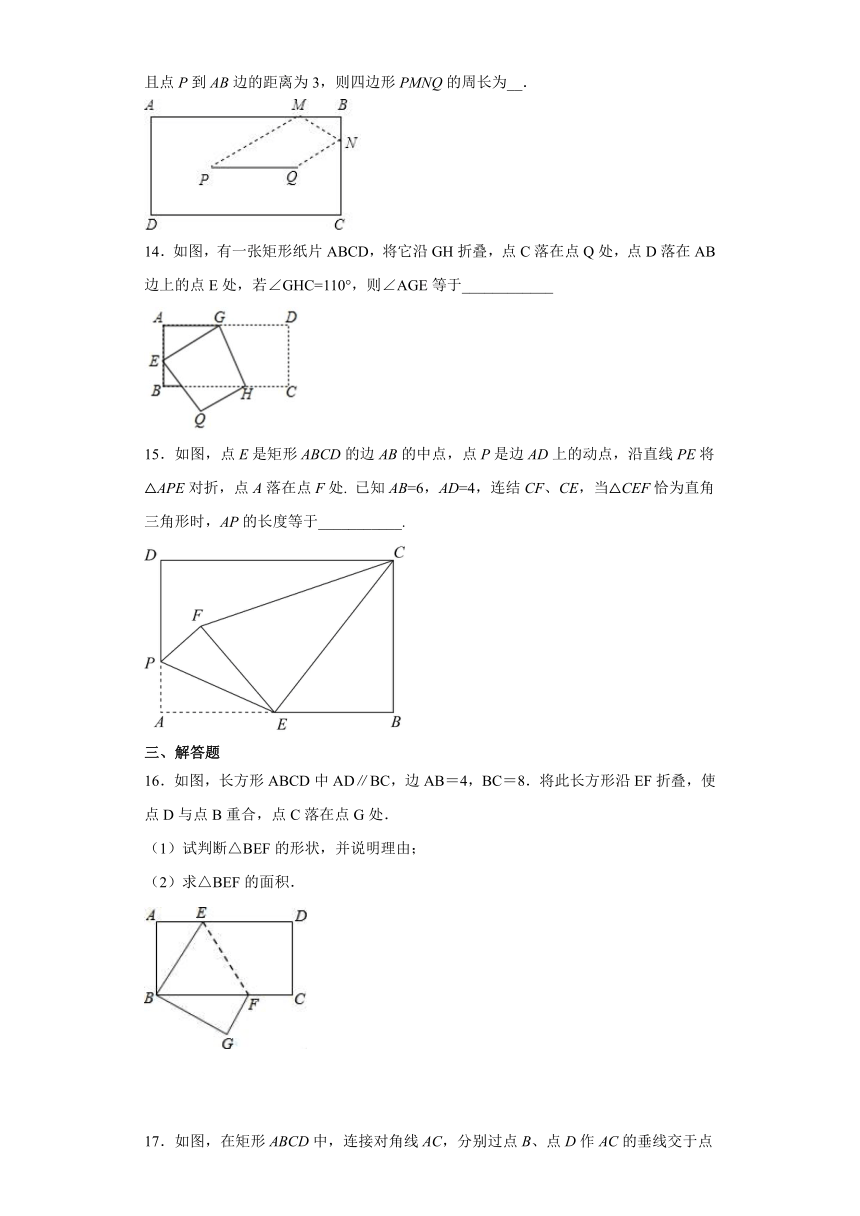
14.如图,有一张矩形纸片ABCD,将它沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠GHC=110°,则∠AGE等于____________
15.如图,点E是矩形ABCD的边AB的中点,点P是边AD上的动点,沿直线PE将△APE对折,点A落在点F处. 已知AB=6,AD=4,连结CF、CE,当△CEF恰为直角三角形时,AP的长度等于___________.
三、解答题
16.如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
17.如图,在矩形ABCD中,连接对角线AC,分别过点B、点D作AC的垂线交于点E、F.证明:AF=CE.
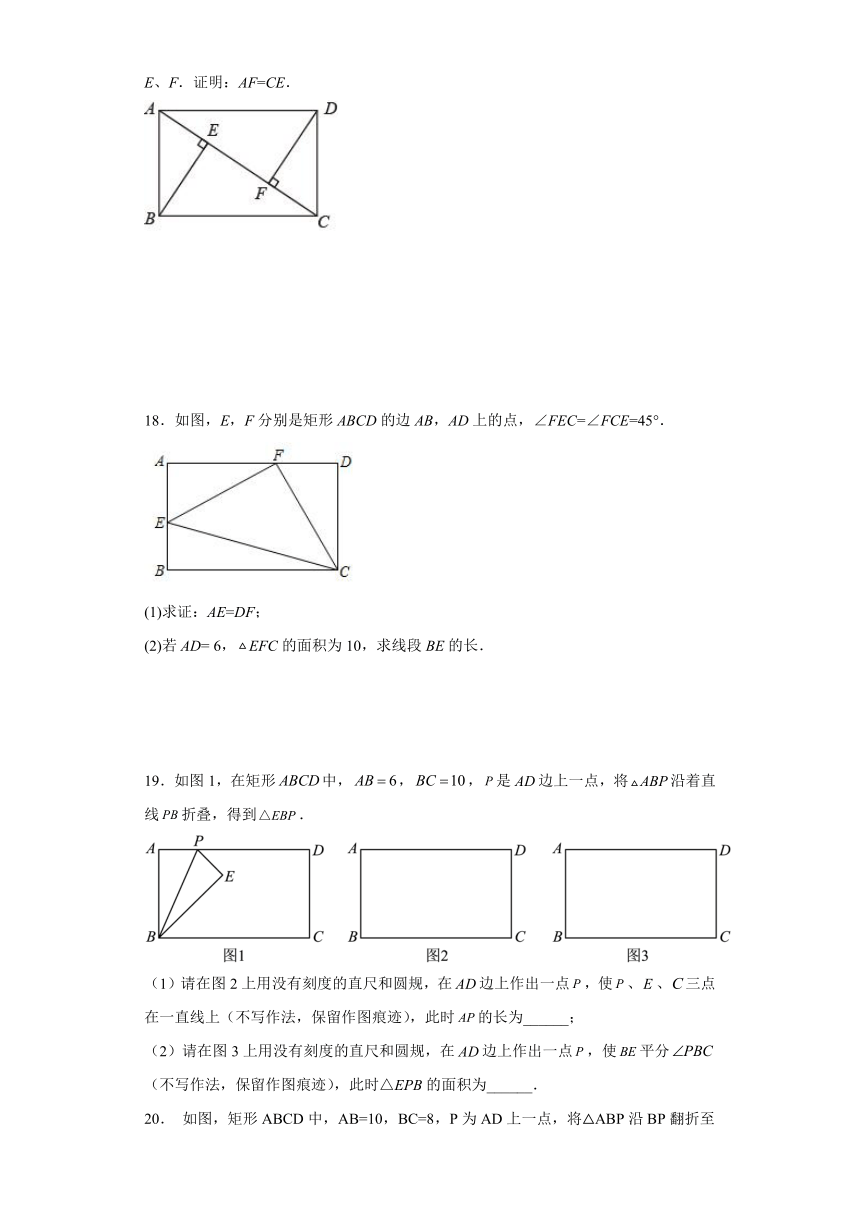
18.如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AE=DF;
(2)若AD= 6,EFC的面积为10,求线段BE的长.
19.如图1,在矩形中,,,是边上一点,将沿着直线折叠,得到.
(1)请在图2上用没有刻度的直尺和圆规,在边上作出一点,使、、三点在一直线上(不写作法,保留作图痕迹),此时的长为______;
(2)请在图3上用没有刻度的直尺和圆规,在边上作出一点,使平分(不写作法,保留作图痕迹),此时△EPB的面积为______.
20. 如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD
(1)求证:△PDO≌△GEO;
(2)求DP的长.
参考答案
1.D
2.B
3.D
4.C
5.D
6.B
7.C
8.A
9.D
10.C
11. 三 直角
12.6
13.16.
14.40°
15.或1
16.(1)△BEF是等腰三角形.
∵ED∥FC,
∴∠DEF=∠BFE,
根据翻折不变性得到∠DEF=∠BEF,
故∠BEF=∠BFE.
∴BE=BF.
△BEF是等腰三角形;
(2)∵矩形ABCD沿EF折叠点B与点D重合,
∴BE=DE,BG=CD,∠EBG=∠ADC=90°,∠G=∠C=90°,
∵AB=CD,
∴AB=BG,
设BE=DE=x,则AE=AB﹣DE=8﹣x,
在Rt△ABE中,AB2+AE2=BE2,
即42+(8﹣x)2=x2,
解得x=5,
∴BE=5,
∵∠ABE+∠EBF=∠ABC=90°,
∠GBF+∠EBF=∠EBG=90°,
∴∠ABE=∠GBF,
在△ABE和△MBF中,
,
∴△ABE≌△GBF(ASA),
∴BF=BE=5,
∴△EBF的面积=×5×4=10.
17.∵四边形ABCD是矩形
∴AD=BC,ADBC
∴∠FAD=∠ECB
∵DF⊥AC,BE⊥AC
∴∠DFA=∠BEC
在Rt△AFD和Rt△CEB中
∴△AFD≌△CEB(AAS)
∴AF=CE
18. (1)证明:∵四边形ABCD是矩形
∴∠A=D=90°
∴∠AEF+∠AFE=90°
∵∠FEC=∠FCE=45°
∴EF=CF,∠EFC=180°-(∠FEC+∠FCE)=90°
∴∠AFE+∠CFD=180°-∠EFC=90°
∴∠AEF=∠CFD
在△AEF和△DFC中,
∴△AEF≌△DFC(AAS)
∴AE=DF
(2)解:∵四边形ABCD是矩形,AD=6
∴BC=AD=6,∠B=90°
由(1)可知∠EFC=90°,EF=CF
∴△EFC的面积=
∵△EFC的面积为10
∴
∴
∴
在Rt△EFC中,∠EFC=90°
∴
在Rt△BCE中,∠B=90°
∴
19.(1)如图(以为圆心,长为半径作弧,此弧与交于点)过B为圆心BP长为半径画弧交CP于H,在分别以P、H为圆心,以BP长为半径画弧,两弧交于F,连结BF,交PC于E,
∵四边形ABCD为矩形,
∴AD∥BC,∠A=90°,∠PEB=90°,
∴∠APB=∠PBC,∠A=∠PEB,
∵BC=PC,
∴∠PBC=∠BPE=∠APB,
在△APB和△EPB中,
,
∴△APB≌△EPB(AAS),
∴AP=EP ,AB=EB,
∴△APB沿BP折叠后与△EPB重合,
∴点P,E,C在同一直线上,
∵,,
∴BE=AB=6,PC=BC=10,
设AP=,则PE=,CE=10-,
在Rt△BCE中,,即
解得
∴
故答案为2;
(2)如图(以为边向右作等边三角形,作的角平分线与交于点)
∵△ABE为等边三角形,
∴∠ABE=60°,
∵BP平分∠ABE,
∴∠ABP=∠EBP=
∵四边形ABCD为矩形,
∴∠ABC=90°,
∴∠EBC=90°-∠ABE=90°-60°=30°=∠PBE,
∴BE平分∠PBC,
∵∠ABP=30°,∠BAP=90°,
∴BP=2AP,
在Rt△ABP中,即,
解得AP=,
∵折叠,
∴PE=AP=,BE=AB=6,
∴S△PBE=.
故答案为.
20.证明:由翻折可得:,,
在△ODP和△OEG中,
∴△PDO≌△GEO(ASA)
(2)∵△PDO≌△GEO;
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=8-x,DG=x,
∴CG=10-x,BG=10-(8-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即64+(10-x)2=(2+x)2,
解得x=
∴DP=
一、单选题
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AC=10,则图中长度为5的线段共有( )
A.2条 B.4条 C.5条 D.6条
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
3.若顺次连接某四边形的四边中点得到一个矩形,则原四边形一定是( )
A.任意四边形 B.对角线相等的四边形 C.平行四边形 D.对角线互相垂直的四边形
4.如图,在矩形中,,相交于点,若的面积是,则矩形的面积是( )
A. B. C. D.
5.如图,在边长为2的等边三角形的外侧作正方形,过点作,垂足为,则的长为( )
A. B. C. D.
6.把一张矩形纸片ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4,BC=8.则△DEF的面积是( )
A.6 B.10 C.12 D.4
7.如图,在矩形中,O为中点,过O点且分别交于F,交于点E,点G是中点且,则下列结论:(1);(2);(3)是等边三角形;(4);其中正确的个数为( )
A.1 B.2 C.3 D.4
8.如图,将一张矩形纸片ABCD折叠,使两个顶点A、C重合,折痕为FG,若AB=4,BC=8,则△ABF的面积是( )
A.6 B.8 C.12 D.24
9.如图,在矩形ABCD中,,的平分线交边BC于点E,于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:,,其中正确命题的序号
A. B. C. D.
10.如图,四边形ABCD是矩形纸片,,对折矩形纸片ABCD,使AD与BC重合,折痕为EF.展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕为BM,再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①;②;③△BMG是等边三角形;④;⑤P为线段BM上一动点,H是线段BN上的动点,则的最小值是.其中正确结论有( )
A.①②③⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
二、填空题
11.有 _____个角是____的四边形是矩形.
12.如图,在中,,点、、分别为、、的中点,若,则的长为______.
13.如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30 ,且点P到AB边的距离为3,则四边形PMNQ的周长为__.
14.如图,有一张矩形纸片ABCD,将它沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠GHC=110°,则∠AGE等于____________
15.如图,点E是矩形ABCD的边AB的中点,点P是边AD上的动点,沿直线PE将△APE对折,点A落在点F处. 已知AB=6,AD=4,连结CF、CE,当△CEF恰为直角三角形时,AP的长度等于___________.
三、解答题
16.如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
17.如图,在矩形ABCD中,连接对角线AC,分别过点B、点D作AC的垂线交于点E、F.证明:AF=CE.
18.如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AE=DF;
(2)若AD= 6,EFC的面积为10,求线段BE的长.
19.如图1,在矩形中,,,是边上一点,将沿着直线折叠,得到.
(1)请在图2上用没有刻度的直尺和圆规,在边上作出一点,使、、三点在一直线上(不写作法,保留作图痕迹),此时的长为______;
(2)请在图3上用没有刻度的直尺和圆规,在边上作出一点,使平分(不写作法,保留作图痕迹),此时△EPB的面积为______.
20. 如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD
(1)求证:△PDO≌△GEO;
(2)求DP的长.
参考答案
1.D
2.B
3.D
4.C
5.D
6.B
7.C
8.A
9.D
10.C
11. 三 直角
12.6
13.16.
14.40°
15.或1
16.(1)△BEF是等腰三角形.
∵ED∥FC,
∴∠DEF=∠BFE,
根据翻折不变性得到∠DEF=∠BEF,
故∠BEF=∠BFE.
∴BE=BF.
△BEF是等腰三角形;
(2)∵矩形ABCD沿EF折叠点B与点D重合,
∴BE=DE,BG=CD,∠EBG=∠ADC=90°,∠G=∠C=90°,
∵AB=CD,
∴AB=BG,
设BE=DE=x,则AE=AB﹣DE=8﹣x,
在Rt△ABE中,AB2+AE2=BE2,
即42+(8﹣x)2=x2,
解得x=5,
∴BE=5,
∵∠ABE+∠EBF=∠ABC=90°,
∠GBF+∠EBF=∠EBG=90°,
∴∠ABE=∠GBF,
在△ABE和△MBF中,
,
∴△ABE≌△GBF(ASA),
∴BF=BE=5,
∴△EBF的面积=×5×4=10.
17.∵四边形ABCD是矩形
∴AD=BC,ADBC
∴∠FAD=∠ECB
∵DF⊥AC,BE⊥AC
∴∠DFA=∠BEC
在Rt△AFD和Rt△CEB中
∴△AFD≌△CEB(AAS)
∴AF=CE
18. (1)证明:∵四边形ABCD是矩形
∴∠A=D=90°
∴∠AEF+∠AFE=90°
∵∠FEC=∠FCE=45°
∴EF=CF,∠EFC=180°-(∠FEC+∠FCE)=90°
∴∠AFE+∠CFD=180°-∠EFC=90°
∴∠AEF=∠CFD
在△AEF和△DFC中,
∴△AEF≌△DFC(AAS)
∴AE=DF
(2)解:∵四边形ABCD是矩形,AD=6
∴BC=AD=6,∠B=90°
由(1)可知∠EFC=90°,EF=CF
∴△EFC的面积=
∵△EFC的面积为10
∴
∴
∴
在Rt△EFC中,∠EFC=90°
∴
在Rt△BCE中,∠B=90°
∴
19.(1)如图(以为圆心,长为半径作弧,此弧与交于点)过B为圆心BP长为半径画弧交CP于H,在分别以P、H为圆心,以BP长为半径画弧,两弧交于F,连结BF,交PC于E,
∵四边形ABCD为矩形,
∴AD∥BC,∠A=90°,∠PEB=90°,
∴∠APB=∠PBC,∠A=∠PEB,
∵BC=PC,
∴∠PBC=∠BPE=∠APB,
在△APB和△EPB中,
,
∴△APB≌△EPB(AAS),
∴AP=EP ,AB=EB,
∴△APB沿BP折叠后与△EPB重合,
∴点P,E,C在同一直线上,
∵,,
∴BE=AB=6,PC=BC=10,
设AP=,则PE=,CE=10-,
在Rt△BCE中,,即
解得
∴
故答案为2;
(2)如图(以为边向右作等边三角形,作的角平分线与交于点)
∵△ABE为等边三角形,
∴∠ABE=60°,
∵BP平分∠ABE,
∴∠ABP=∠EBP=
∵四边形ABCD为矩形,
∴∠ABC=90°,
∴∠EBC=90°-∠ABE=90°-60°=30°=∠PBE,
∴BE平分∠PBC,
∵∠ABP=30°,∠BAP=90°,
∴BP=2AP,
在Rt△ABP中,即,
解得AP=,
∵折叠,
∴PE=AP=,BE=AB=6,
∴S△PBE=.
故答案为.
20.证明:由翻折可得:,,
在△ODP和△OEG中,
∴△PDO≌△GEO(ASA)
(2)∵△PDO≌△GEO;
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=8-x,DG=x,
∴CG=10-x,BG=10-(8-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即64+(10-x)2=(2+x)2,
解得x=
∴DP=
