2023届高考考前(悟通法 得满分)(悟通法 得满分)第2讲 六大常用方法(增分有招) 课件(共37张)
文档属性
| 名称 | 2023届高考考前(悟通法 得满分)(悟通法 得满分)第2讲 六大常用方法(增分有招) 课件(共37张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 21:18:46 | ||
图片预览







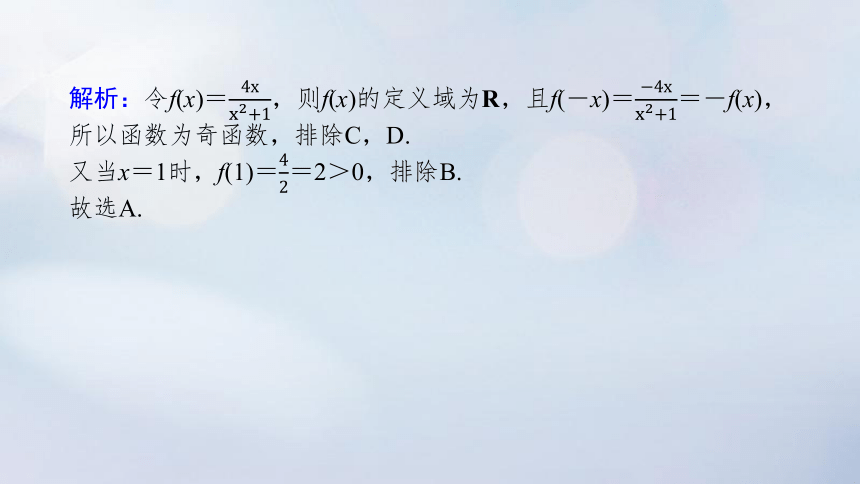



文档简介
(共37张PPT)
第2讲 六大常用方法(增分有招)
高考客观题分为选择题与填空题,选择题是属于“小灵通”题,其解题过程“不讲道理”,所以解答选择题的基本策略是:充分地利用题干和选项两方面的条件所提供的信息作出判断,先定性后定量,先特殊后推理,先间接后直接,先排除后求解.而填空题是不要求写出计算或推理过程,只需要将结论直接写出的“求解题”.解答选择题与填空题的方法一般有直接法、特例法、数形结合法(图解法)、估算法、构造法、排除法等.
方法 1 直接法
方法诠释 直接从题设的条件出发,利用已知条件、相关公式、公理、定理、法则,通过准确的运算、严谨的推理、合理的验证得出正确的结论,然后对照题目所给出的选项“对号入座”作出相应的选择,从而确定正确选项的方法.
适用范围 涉及概念、性质的辨析或运算,较简单的题目常用直接法.
例 1 [2022·湖南湘潭三模]已知集合A={x| x2-7x+12≤0},B=,若A B,则m的取值范围为( )
A.(-6,+∞) B.[-6,+∞)
C.(-∞,-6) D.(-∞,-6]
答案:A
解析:因为A={x|3≤x≤4},B=,A B,所以-<3,解得m>-6.故选A.
名师点题
直接法的使用技巧
直接法是解决计算型客观题最常用的方法,在计算过程中,我们要根据题目的要求灵活处理,多角度思考问题,注意一些解题规律和解题技巧的灵活应用,将计算过程简化,从而得到结果,这是快速准确求解客观题的关键.
对 点 训 练
[2022·广西崇左模拟]已知复数z=1-3i,那么=( )
A.i B.i
C.-i D.-i
答案:A
解析:====.故选A.
方法 2 排除法
方法诠释 排除法也叫筛选法或淘汰法,使用排除法的前提条件是答案唯一,具体的做法是采用简捷有效的手段对各个备选答案进行“筛选”,将其中与题干相矛盾的干扰项逐一排除,从而获得正确结论.
适用范围 这种方法适用于直接法解决问题很困难或者计算较繁琐的情况.
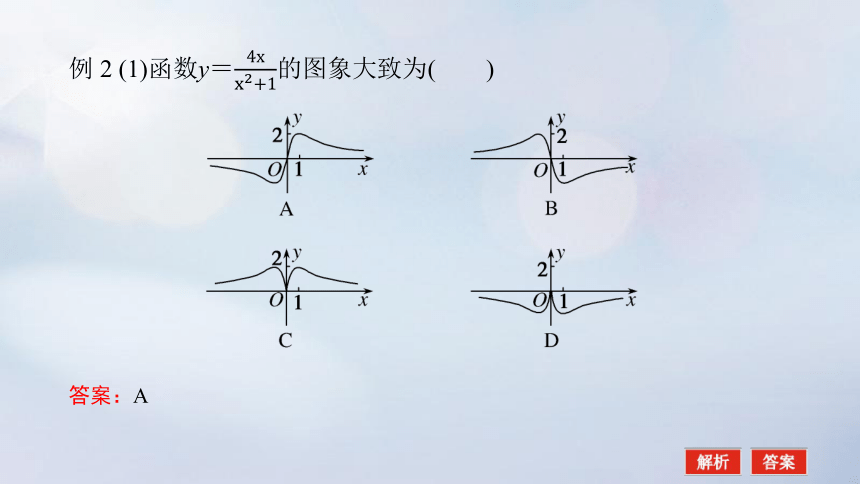
例 2 (1)函数y=的图象大致为( )
答案:A
解析:令f(x)=,则f(x)的定义域为R,且f(-x)==-f(x),
所以函数为奇函数,排除C,D.
又当x=1时,f(1)==2>0,排除B.
故选A.
(2)[2021·全国甲卷,文]下列函数中是增函数的为( )
A.f(x)=-x B.f(x)=
C.f(x)=x2 D.f(x)=
答案:D
解析:取x1=-1,x2=0,对于A项有f(x1)=1,f(x2)=0,所以A项不符合题意;对于B项有f(x1)=,f(x2)=1,所以B项不符合题意;对于C项有f(x1)=1,f(x2)=0,所以C项不符合题意.故选D.
名师点题
排除法的使用技巧
排除法适用于不易直接求解的选择题.当题目中的条件多于一个时,先根据某些条件找出明显与之矛盾的选项予以否定,再根据另一些条件在缩小的范围内找出矛盾,这样逐步排除,直接得到正确的选项.
对 点 训 练
已知函数f(x)=x(1+a|x|).设关于x的不等式f(x+a)A.(,0) B.(,0)
C.(,0)) D.(-∞,)
答案:A
解析:当x=0时,有f(a)方法 3 特例法
方法诠释 从题干(或选项)出发,通过选取构造特殊情况代入,将问题特殊化,再进行判断.特殊化法是“小题小做”的重要策略,要注意在怎样的情况下才可使用,特殊情况可能是:特殊值、特殊点、特殊位置、特殊数列等.
适用范围 适用于题目中含有字母或具有一般性结论的选择题.
例 3 (1)设四边形ABCD为平行四边形,||=6,||=4,若点M,N满足=3=2,则·等于( )
A.20 B.15
C.9 D.6
答案:C
解析:若四边形ABCD为矩形,建系如图,由=3=2,知M(6,3),N(4,4),所以=(6,3),=(2,-1),所以·=6×2+3×(-1)=9.故选C.
(2)设椭圆C:=1的长轴的两端点分别是M,N,P是C上异于M,N的任意一点,则直线PM与PN的斜率之积等于________.
-
解析:取特殊点,设P为椭圆的短轴的一个端点(0,),又M(-2,0),N(2,0),所以kPM·kPN==-.
名师点题
特例法具有简化运算和推理的优点,比较适用于题目中含有字母或具有一般性结论的选择题或填空题,但用特例法解题时,要注意以下几点:
第一,取特例尽可能简单,有利于计算和推理;
第二,若在不同的特殊情况下有两个或两个以上的结论相符,则应选另一特例情况再检验,或改用其他方法求解;
第三,对于开放性的问题或者有多种答案的填空题,不能使用该种方法求解.
对 点 训 练
已知O是锐角△ABC的外接圆圆心,∠A=60°,··=2m·,则m的值为( )
A. B.
C.1 D.
答案:A
解析:如图,当△ABC为正三角形时,A=B=C=60°,取D为BC的中点,
=,则有=2m·,
∴=2m×,
∴=,
∴m=,故选A.
方法 4 数形结合法
方法 诠释 根据题设条件作出所研究问题的曲线或有关图形,借助几何图形的直观性给出正确的判断,习惯上也叫数形结合法.
有些选择题可通过命题条件中的函数关系或几何意义,作出函数的图象或几何图形,借助于图象或图形的作法、形状、位置、性质等,综合图象的特征,得出结论.
图形化策略就是以数形结合的数学思想为指导的一种解题策略.
适用 范围 适用于求解问题中含有几何意义命题的.
例 4 若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数f(x)=则此函数的“友好点对”有( )
A.0对 B.1对
C.2对 D.3对
答案:C
解析:根据题意,将函数f(x)=-x2-4x(x≤0)的图象绕原点旋转180°后,得到的图象所对应的解析式为y=x2-4x(x≥0),再作出函数y=log2x(x>0)的图象,如图所示.由题意,知函数y=x2-4x(x>0)的图象与函数f(x)=log2x(x>0)的图象的交点个数即为“友好点对”的对数.由图可知它们的图象交点有2个,所以此函数的“友好点对”有2对.故选C.
名师点题
图解法实质上就是数形结合的思想方法在解题中的应用,利用图形的直观性并结合所学知识便可直接得到相应的结论,这也是高考命题的热点.准确运用此类方法的关键是正确把握各种式子与几何图形中的变量之间的对应关系,利用几何图形中的相关结论求出结果.
对 点 训 练
1.已知非零向量a,b,c满足a+b+c=0,向量a,b的夹角为120°,且|b|=2|a|,则向量a与c的夹角为( )
A.60° B.90°
C.120° D.150°
答案:B
解析:如图,因为〈a,b〉=120°,|b|=2|a|,a+b+c=0,所以在△OBC中,BC与CO的夹角为90°,即a与c的夹角为90°.故选B.
2.已知函数f(x)=若|f(x)|≥ax,则a的取值范围是( )
A.(-∞,0] B.(-∞,1]
C.[-2,1] D.[-2,0]
答案:D
解析:函数y=|f(x)|的图象如图所示.
①当a=0时,|f(x)|≥ax显然成立.
②当a>0时,只需在x>0时,ln (x+1)≥ax成立.比较对数函数与一次函数y=ax的增长速度.显然不存在a>0使ln (x+1)≥ax在x>0上恒成立.
③当a<0时,只需x<0时,x2-2x≥ax成立,即a≥x-2成立,∴a≥-2.
综上所述:-2≤a≤0.故选D.
方法 5 构造法
方法 诠释 构造型客观题的求解,需要利用已知条件和结论的特殊性构造出新的数学模型(如构造函数、方程或图形),从而简化推理与计算过程,使较复杂的数学问题得到简捷地解决,它来源于对基础知识和基本方法的积累,需要从一般的方法原理中进行提炼概括,积极联想,横向类比,从曾经遇到过的类似问题中寻找灵感.
适用 范围 构造出相应的函数、几何图象等具体的数学模型问题.
例 5 (1)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )
A.8π B.4π
C.2π D.π
答案:D
解析:如图所示,构造棱长为的正方体PBJA-CDHG,显然满足题设的一切条件,则球O就是该正方体的外接球,从而体积为π.故选D.
(2)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是_______________.
(-∞,-1)
解析:构造函数g(x)=,
则g′(x)=.根据条件,g(x)为偶函数,
且x>0时,g′(x)<0,g(x)为减函数,
g(-1)=g(1)=0.
∴当00,∴f(x)>0,
同理当x<-1时,g(x)<0,∴f(x)>0,
故使得f(x)>0成立的x的取值范围是(-∞,-1)
名师点题
构造法实质上是转化与化归思想在解题中的应用,需要根据已知条件和所要解决的问题确定构造的方向.一般通过构造新的函数、不等式或数列等新的模型将问题转化为自己熟悉的问题.在立体几何中,补形构造是最为常用的解题技巧.通过补形能将一般几何体的有关问题在特殊的几何体中求解,如将三棱锥补成特殊的长方体等.
对 点 训 练
已知函数f(x)是定义在R上的可导函数,且对于 x∈R,均有f(x)>f′(x),则有( )
A.e2 018f(-2 018)e2 018f(0)
B.e2 018f(-2 018)C.e2 018f(-2 018)>f(0),f(2 018)>e2 018f(0)
D.e2 018f(-2 018)>f(0),f(2 018)答案:D
解析:构造函数g(x)=,则g′(x)==,
因为 x∈R,均有f(x)>f′(x),并且ex>0,所以g′(x)<0,故函数g(x)=在R上单调递减,
所以g(-2 018)>g(0),g(2 018)f(0),也就是e2 018f(-2 018)>f(0),f(2 018)方法 6 估值法
方法诠释 估值法就是不需要计算出代数式的准确数值,通过估计其大致取值范围从而解决相应问题的方法.该种方法主要适用于比较大小的有关问题,尤其是在选择题或填空题中,解答不需要详细的过程,因此可以猜测、合情推理、估算而获得,从而减少运算量.
适用范围 近几年的高考题连续出现了一些估值、估算题,这类题主要考查了考生的估算能力.是一种粗略的计算方法.
例 6 (1) 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是( )
A.165 cm B.175 cm
C.185 cm D.190 cm
答案:B
解析:头顶至脖子下端的长度为26 cm,可得咽喉至肚脐的长度小于42 cm,肚脐至足底的长度小于110 cm,则该人的身高小于178 cm,又由肚脐至足底的长度大于105 cm,可得头顶至肚脐的长度大于65 cm,则该人的身高大于170 cm,所以该人的身高在170 cm~178 cm之间,选B.
(2)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D ABC体积的最大值为( )
A.12 B.18
C.24 D.54
答案:B
解析:等边三角形ABC的面积为9,显然球心不是此三角形的中心,所以三棱锥的体积最大时,三棱锥的高h应满足h=6,所以(VD ABC)max=×9×6=18.故选B.
名师点题
估算法是根据变量变化的趋势或极值的取值情况进行求解的方法.当题目从正面解析比较麻烦,特值法又无法确定正确的选项时,如难度稍大的函数的最值或取值范围、函数图象的变化等问题,常用此种方法确定选项.
对 点 训 练
图中阴影部分的面积S是h的函数(0≤h≤H),则该函数的大致图象是( )
答案:B
解析:由题图知,随着h的增大,阴影部分的面积S逐渐减小,且减小得越来越慢,结合选项可知选B.
第2讲 六大常用方法(增分有招)
高考客观题分为选择题与填空题,选择题是属于“小灵通”题,其解题过程“不讲道理”,所以解答选择题的基本策略是:充分地利用题干和选项两方面的条件所提供的信息作出判断,先定性后定量,先特殊后推理,先间接后直接,先排除后求解.而填空题是不要求写出计算或推理过程,只需要将结论直接写出的“求解题”.解答选择题与填空题的方法一般有直接法、特例法、数形结合法(图解法)、估算法、构造法、排除法等.
方法 1 直接法
方法诠释 直接从题设的条件出发,利用已知条件、相关公式、公理、定理、法则,通过准确的运算、严谨的推理、合理的验证得出正确的结论,然后对照题目所给出的选项“对号入座”作出相应的选择,从而确定正确选项的方法.
适用范围 涉及概念、性质的辨析或运算,较简单的题目常用直接法.
例 1 [2022·湖南湘潭三模]已知集合A={x| x2-7x+12≤0},B=,若A B,则m的取值范围为( )
A.(-6,+∞) B.[-6,+∞)
C.(-∞,-6) D.(-∞,-6]
答案:A
解析:因为A={x|3≤x≤4},B=,A B,所以-<3,解得m>-6.故选A.
名师点题
直接法的使用技巧
直接法是解决计算型客观题最常用的方法,在计算过程中,我们要根据题目的要求灵活处理,多角度思考问题,注意一些解题规律和解题技巧的灵活应用,将计算过程简化,从而得到结果,这是快速准确求解客观题的关键.
对 点 训 练
[2022·广西崇左模拟]已知复数z=1-3i,那么=( )
A.i B.i
C.-i D.-i
答案:A
解析:====.故选A.
方法 2 排除法
方法诠释 排除法也叫筛选法或淘汰法,使用排除法的前提条件是答案唯一,具体的做法是采用简捷有效的手段对各个备选答案进行“筛选”,将其中与题干相矛盾的干扰项逐一排除,从而获得正确结论.
适用范围 这种方法适用于直接法解决问题很困难或者计算较繁琐的情况.
例 2 (1)函数y=的图象大致为( )
答案:A
解析:令f(x)=,则f(x)的定义域为R,且f(-x)==-f(x),
所以函数为奇函数,排除C,D.
又当x=1时,f(1)==2>0,排除B.
故选A.
(2)[2021·全国甲卷,文]下列函数中是增函数的为( )
A.f(x)=-x B.f(x)=
C.f(x)=x2 D.f(x)=
答案:D
解析:取x1=-1,x2=0,对于A项有f(x1)=1,f(x2)=0,所以A项不符合题意;对于B项有f(x1)=,f(x2)=1,所以B项不符合题意;对于C项有f(x1)=1,f(x2)=0,所以C项不符合题意.故选D.
名师点题
排除法的使用技巧
排除法适用于不易直接求解的选择题.当题目中的条件多于一个时,先根据某些条件找出明显与之矛盾的选项予以否定,再根据另一些条件在缩小的范围内找出矛盾,这样逐步排除,直接得到正确的选项.
对 点 训 练
已知函数f(x)=x(1+a|x|).设关于x的不等式f(x+a)
C.(,0)) D.(-∞,)
答案:A
解析:当x=0时,有f(a)
方法诠释 从题干(或选项)出发,通过选取构造特殊情况代入,将问题特殊化,再进行判断.特殊化法是“小题小做”的重要策略,要注意在怎样的情况下才可使用,特殊情况可能是:特殊值、特殊点、特殊位置、特殊数列等.
适用范围 适用于题目中含有字母或具有一般性结论的选择题.
例 3 (1)设四边形ABCD为平行四边形,||=6,||=4,若点M,N满足=3=2,则·等于( )
A.20 B.15
C.9 D.6
答案:C
解析:若四边形ABCD为矩形,建系如图,由=3=2,知M(6,3),N(4,4),所以=(6,3),=(2,-1),所以·=6×2+3×(-1)=9.故选C.
(2)设椭圆C:=1的长轴的两端点分别是M,N,P是C上异于M,N的任意一点,则直线PM与PN的斜率之积等于________.
-
解析:取特殊点,设P为椭圆的短轴的一个端点(0,),又M(-2,0),N(2,0),所以kPM·kPN==-.
名师点题
特例法具有简化运算和推理的优点,比较适用于题目中含有字母或具有一般性结论的选择题或填空题,但用特例法解题时,要注意以下几点:
第一,取特例尽可能简单,有利于计算和推理;
第二,若在不同的特殊情况下有两个或两个以上的结论相符,则应选另一特例情况再检验,或改用其他方法求解;
第三,对于开放性的问题或者有多种答案的填空题,不能使用该种方法求解.
对 点 训 练
已知O是锐角△ABC的外接圆圆心,∠A=60°,··=2m·,则m的值为( )
A. B.
C.1 D.
答案:A
解析:如图,当△ABC为正三角形时,A=B=C=60°,取D为BC的中点,
=,则有=2m·,
∴=2m×,
∴=,
∴m=,故选A.
方法 4 数形结合法
方法 诠释 根据题设条件作出所研究问题的曲线或有关图形,借助几何图形的直观性给出正确的判断,习惯上也叫数形结合法.
有些选择题可通过命题条件中的函数关系或几何意义,作出函数的图象或几何图形,借助于图象或图形的作法、形状、位置、性质等,综合图象的特征,得出结论.
图形化策略就是以数形结合的数学思想为指导的一种解题策略.
适用 范围 适用于求解问题中含有几何意义命题的.
例 4 若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数f(x)=则此函数的“友好点对”有( )
A.0对 B.1对
C.2对 D.3对
答案:C
解析:根据题意,将函数f(x)=-x2-4x(x≤0)的图象绕原点旋转180°后,得到的图象所对应的解析式为y=x2-4x(x≥0),再作出函数y=log2x(x>0)的图象,如图所示.由题意,知函数y=x2-4x(x>0)的图象与函数f(x)=log2x(x>0)的图象的交点个数即为“友好点对”的对数.由图可知它们的图象交点有2个,所以此函数的“友好点对”有2对.故选C.
名师点题
图解法实质上就是数形结合的思想方法在解题中的应用,利用图形的直观性并结合所学知识便可直接得到相应的结论,这也是高考命题的热点.准确运用此类方法的关键是正确把握各种式子与几何图形中的变量之间的对应关系,利用几何图形中的相关结论求出结果.
对 点 训 练
1.已知非零向量a,b,c满足a+b+c=0,向量a,b的夹角为120°,且|b|=2|a|,则向量a与c的夹角为( )
A.60° B.90°
C.120° D.150°
答案:B
解析:如图,因为〈a,b〉=120°,|b|=2|a|,a+b+c=0,所以在△OBC中,BC与CO的夹角为90°,即a与c的夹角为90°.故选B.
2.已知函数f(x)=若|f(x)|≥ax,则a的取值范围是( )
A.(-∞,0] B.(-∞,1]
C.[-2,1] D.[-2,0]
答案:D
解析:函数y=|f(x)|的图象如图所示.
①当a=0时,|f(x)|≥ax显然成立.
②当a>0时,只需在x>0时,ln (x+1)≥ax成立.比较对数函数与一次函数y=ax的增长速度.显然不存在a>0使ln (x+1)≥ax在x>0上恒成立.
③当a<0时,只需x<0时,x2-2x≥ax成立,即a≥x-2成立,∴a≥-2.
综上所述:-2≤a≤0.故选D.
方法 5 构造法
方法 诠释 构造型客观题的求解,需要利用已知条件和结论的特殊性构造出新的数学模型(如构造函数、方程或图形),从而简化推理与计算过程,使较复杂的数学问题得到简捷地解决,它来源于对基础知识和基本方法的积累,需要从一般的方法原理中进行提炼概括,积极联想,横向类比,从曾经遇到过的类似问题中寻找灵感.
适用 范围 构造出相应的函数、几何图象等具体的数学模型问题.
例 5 (1)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )
A.8π B.4π
C.2π D.π
答案:D
解析:如图所示,构造棱长为的正方体PBJA-CDHG,显然满足题设的一切条件,则球O就是该正方体的外接球,从而体积为π.故选D.
(2)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是_______________.
(-∞,-1)
解析:构造函数g(x)=,
则g′(x)=.根据条件,g(x)为偶函数,
且x>0时,g′(x)<0,g(x)为减函数,
g(-1)=g(1)=0.
∴当0
同理当x<-1时,g(x)<0,∴f(x)>0,
故使得f(x)>0成立的x的取值范围是(-∞,-1)
名师点题
构造法实质上是转化与化归思想在解题中的应用,需要根据已知条件和所要解决的问题确定构造的方向.一般通过构造新的函数、不等式或数列等新的模型将问题转化为自己熟悉的问题.在立体几何中,补形构造是最为常用的解题技巧.通过补形能将一般几何体的有关问题在特殊的几何体中求解,如将三棱锥补成特殊的长方体等.
对 点 训 练
已知函数f(x)是定义在R上的可导函数,且对于 x∈R,均有f(x)>f′(x),则有( )
A.e2 018f(-2 018)
B.e2 018f(-2 018)
D.e2 018f(-2 018)>f(0),f(2 018)
解析:构造函数g(x)=,则g′(x)==,
因为 x∈R,均有f(x)>f′(x),并且ex>0,所以g′(x)<0,故函数g(x)=在R上单调递减,
所以g(-2 018)>g(0),g(2 018)
方法诠释 估值法就是不需要计算出代数式的准确数值,通过估计其大致取值范围从而解决相应问题的方法.该种方法主要适用于比较大小的有关问题,尤其是在选择题或填空题中,解答不需要详细的过程,因此可以猜测、合情推理、估算而获得,从而减少运算量.
适用范围 近几年的高考题连续出现了一些估值、估算题,这类题主要考查了考生的估算能力.是一种粗略的计算方法.
例 6 (1) 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是( )
A.165 cm B.175 cm
C.185 cm D.190 cm
答案:B
解析:头顶至脖子下端的长度为26 cm,可得咽喉至肚脐的长度小于42 cm,肚脐至足底的长度小于110 cm,则该人的身高小于178 cm,又由肚脐至足底的长度大于105 cm,可得头顶至肚脐的长度大于65 cm,则该人的身高大于170 cm,所以该人的身高在170 cm~178 cm之间,选B.
(2)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D ABC体积的最大值为( )
A.12 B.18
C.24 D.54
答案:B
解析:等边三角形ABC的面积为9,显然球心不是此三角形的中心,所以三棱锥的体积最大时,三棱锥的高h应满足h=6,所以(VD ABC)max=×9×6=18.故选B.
名师点题
估算法是根据变量变化的趋势或极值的取值情况进行求解的方法.当题目从正面解析比较麻烦,特值法又无法确定正确的选项时,如难度稍大的函数的最值或取值范围、函数图象的变化等问题,常用此种方法确定选项.
对 点 训 练
图中阴影部分的面积S是h的函数(0≤h≤H),则该函数的大致图象是( )
答案:B
解析:由题图知,随着h的增大,阴影部分的面积S逐渐减小,且减小得越来越慢,结合选项可知选B.
同课章节目录
