(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题六 函数与导数 第4讲 导数的综合应用 课件(51张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题六 函数与导数 第4讲 导数的综合应用 课件(51张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 05:55:14 | ||
图片预览




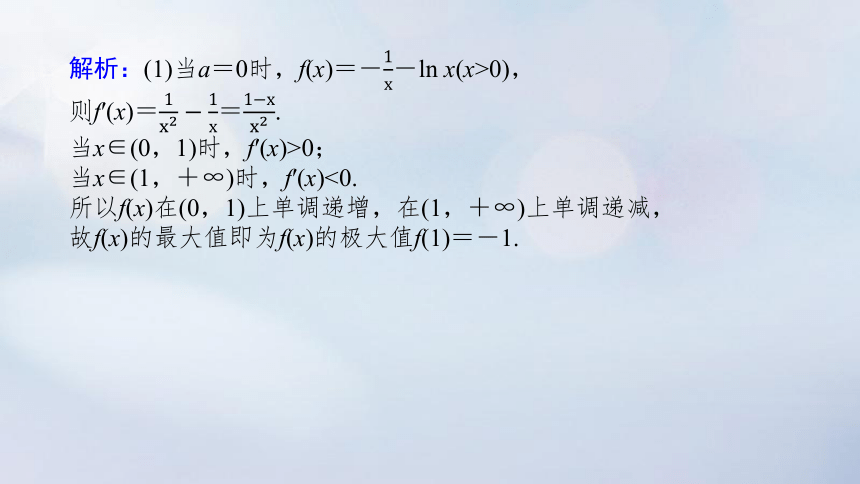





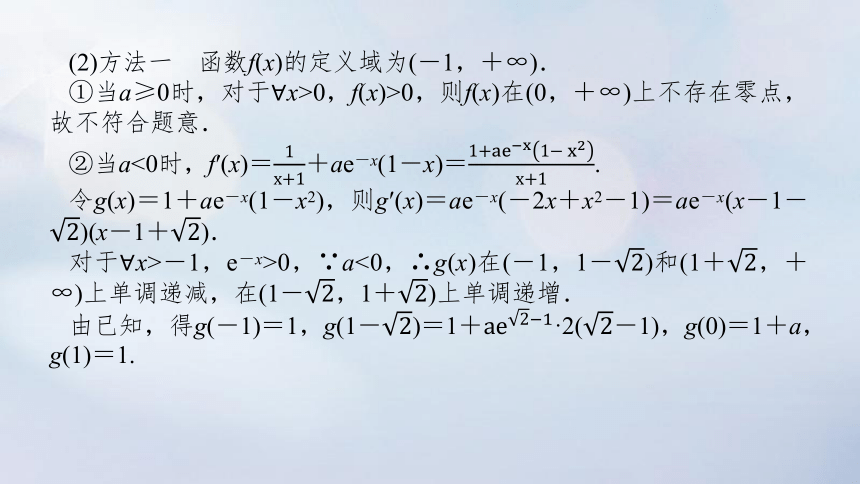
文档简介
(共51张PPT)
第4讲 导数的综合应用
考点一
考点二
考点三
考点一
利用导数研究函数的零点
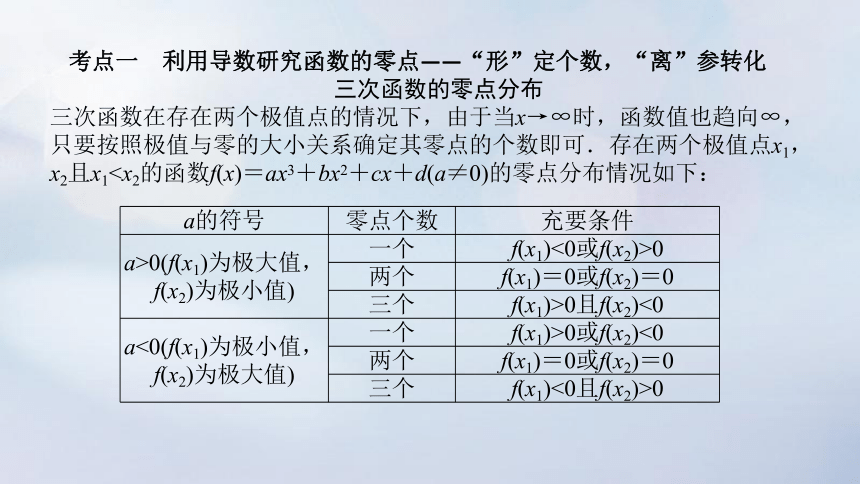
考点一 利用导数研究函数的零点——“形”定个数,“离”参转化
三次函数的零点分布
三次函数在存在两个极值点的情况下,由于当x→∞时,函数值也趋向∞,只要按照极值与零的大小关系确定其零点的个数即可.存在两个极值点x1,x2且x1a的符号 零点个数 充要条件
a>0(f(x1)为极大值,f(x2)为极小值) 一个 f(x1)<0或f(x2)>0
两个 f(x1)=0或f(x2)=0
三个 f(x1)>0且f(x2)<0
a<0(f(x1)为极小值,f(x2)为极大值) 一个 f(x1)>0或f(x2)<0
两个 f(x1)=0或f(x2)=0
三个 f(x1)<0且f(x2)>0
例 1 [2022·全国乙卷(文)]已知函数f(x)=ax--(a+1)ln x.
(1)当a=0时,求f(x)的最大值;
(2)若f(x)恰有一个零点,求a的取值范围.
解析:(1)当a=0时,f(x)=--ln x(x>0),
则f′(x)==.
当x∈(0,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0.
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故f(x)的最大值即为f(x)的极大值f(1)=-1.
(2)因为函数f(x)恰有一个零点,所以方程a(x-ln x)--ln x=0在(0,+∞)上恰有一个解,即方程a(x-ln x)=+ln x在(0,+∞)上恰有一个解.
又易知当x>0时,x-ln x>0,
所以方程a=在(0,+∞)上恰有一个解.
令g(x)=(x>0),
则g′(x)=.
令h(x)=x-1-(x+1)ln x(x>0),
则h′(x)=1-ln x-=-ln x-.
由(1)知,h′(x)≤-1,
所以h(x)在(0,+∞)上单调递减.
又h(1)=0,所以当x∈(0,1]时,h(x)≥0;
当x∈(1,+∞)时,h(x)<0.
则当x∈(0,1]时,g′(x)≤0;
当x∈(1,+∞)时,g′(x)<0.
所以g(x)在(0,+∞)上单调递减.
又当x→0时,g(x)→+∞,当x→+∞时,g(x)→0,所以a∈(0,+∞).
归纳总结
利用导数研究函数零点问题的思路
(1)构建函数g(x)(要求g′(x)易求,g′(x)=0可解),转化为确定g(x)的零点个数问题求解,利用导数研究该函数的单调性、极值,并确定定义区间端点值的符号(或变化趋势)等,画出g(x)的图象草图,数形结合求解.
(2)利用零点存在性定理:先用该定理判断函数在某区间上有零点,然后利用导数研究函数的单调性、极值(最值)及区间端点值符号,进而判断函数在该区间上零点的个数.
对点训练
[2022·全国乙卷(理)]已知函数f(x)=ln (1+x)+axe-x.
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.
解析:(1)当a=1时,f(x)=ln (1+x)+xe-x,
则f′(x)=,∴f(0)=0,f′(0)=2,
∴曲线y=f(x)在点(0,f(0))处的切线方程为y=2x,即2x-y=0.
(2)方法一 函数f(x)的定义域为(-1,+∞).
①当a≥0时,对于 x>0,f(x)>0,则f(x)在(0,+∞)上不存在零点,故不符合题意.
②当a<0时,f′(x)=+ae-x(1-x)=.
令g(x)=1+ae-x(1-x2),则g′(x)=ae-x(-2x+x2-1)=ae-x(x-1-)(x-1+).
对于 x>-1,e-x>0,∵a<0,∴g(x)在(-1,1-)和(1+,+∞)上单调递减,在(1-,1+)上单调递增.
由已知,得g(-1)=1,g(1-)=1+·2(-1),g(0)=1+a,g(1)=1.
(ⅰ)若-1≤a≤0,则有:
当0g(0)=1+a≥0;
当x>1时,由于1-x2<0,ae-x<0,故g(x)=1+ae-x(1-x2)>1>0.
综上可知,当x>0时,都有g(x)>0,则f′(x)=>0,
∴f(x)在(0,+∞)上单调递增.
∴对于 x>0,f(x)>f(0)=0,f(x)在(0,+∞)上不存在零点,符合题意.
(ⅱ)当a<-1时,g(1-)又∵g(-1)=1>0,∴ x0∈(-1,0),满足g(x0)=0,
且 x∈(-1,x0),都有g(x)>0,则f′(x)=>0,
x∈(x0,0),都有g(x)<0,则f′(x)=<0,
∴f(x)在(-1,x0)上单调递增,在(x0,0)上单调递减.
又∵f(0)=0,∴f(x0)>0.
又∵当x→-1时,f(x)→-∞,
∴f(x)在(-1,0)上恰有一个零点.
∵g(0)=1+a<0,g(1)=1>0,g(x)在(0,1+)上单调递增,在[1+,+∞)上单调递减,
∴ x1∈(0,1),满足g(x1)=0,且当x∈(0,x1)时,g(x)<0,则f′(x)=<0,当x∈(x1,1)时,g(x)>0,则f′(x)=>0.
又∵当x≥1时,ae-x<0,1-x2≤0,
∴g(x)=1+ae-x·(1-x2)>0,∴f′(x)=>0,
∴f(x)在(0,x1)上单调递减,在[x1,+∞)上单调递增.
又∵f(0)=0,∴ x∈(0,x1),f(x)<0,则f(x1)<0.
又∵当x→+∞时,ln (1+x)→+∞,axe-x→0,
∴f(x)→+∞,
∴f(x)在(x1,+∞)上存在零点,且仅有一个.
故f(x)在(0,+∞)上恰有一个零点.
综上可知,满足题意的a的取值范围是(-∞,-1).
方法二 令g(x)=.
f(x)在区间(-1,0),(0,+∞)上各恰有一个零点等价于g(x)==-a在(-1,0),(0,+∞)上各恰有一解.
g′(x)=.
令h(x)=(x-1)ln (1+x)+,
则h′(x)=ln (1+x)+.
令φ(x)=ln (1+x)+,
则φ′(x)=.
①当x∈(0,+∞)时,φ′(x)>0,则h′(x)>h′(0)=0,
∴h(x)>h(0)=0,∴g′(x)>0,∴g(x)在(0,+∞)上单调递增.
又∵当x→0时,g(x)==1,当x→+∞时,g(x)→+∞,∴a∈(-∞,-1).
②当x∈(-1,-2)时,φ′(x)<0;当x∈(-2,0)时,φ′(x)>0.
∵当x→-1时,φ(x)=h′(x)→+∞,h′(0)=0,
∴存在a1∈(-1,0)使h′(a1)=0,
∴h(x)在(-1,a1)上单调递增,在(a1,0)上单调递减.
当x→-1时,h(x)→-∞.
又h(0)=0,
∴存在a2∈(-1,a1),使得h(a2)=0,
即g(x)在(-1,a2)上单调递减,在(a2,0)上单调递增.
当x→-1时,g(x)→+∞;
当x→0时,g(x)→1,g(x)的大致图象如图.
故当a∈(-∞,-1)时,
g(x)=-a仅有一解;
当a∈(-1,-g(a2))时,g(x)=-a有两解.
综上可知,a∈(-∞,-1).
考点二
利用导数证明不等式
考点二 利用导数证明不等式——构造·分离·放缩
常见的指数、对数不等式
(1)ex≥x+1及其变形ex-1≥x,ex≥ex等.
(2)ln x≤x-1(x>0)及其变式ln (x+1)≤x,ln x≥1-等.
例 2 [2022·湖北二模]已知函数f(x)=xex-1,g(x)=a(ln x+x).
(1)若不等式f(x)≥g(x)恒成立,求正实数a的值;
(2)证明:x2ex>(x+2)ln x+2sin x.
解析: (1)令h(x)=f(x)-g(x)=xex-a(ln x+x)-1,
则h′(x)=(x+1)ex-a=(x>0),
设φ(x)=xex-a(a>0),则φ′(x)=(x+1)ex>0对任意x>0恒成立,
所以φ(x)在(0,+∞)上单调递增,
又φ(0)=-a<0,φ(a)=aea-a=a(ea-1)>0,存在唯一实数x0∈(0,a),φ(x0)=0,
所以当x∈(0,x0)时,h′(x)=<0,h(x)单调递减;
当x∈(x0,+∞)时,h′(x)=>0,h(x)单调递增;
所以h(x)min=h(x0)=-a(x0+ln x0)-1.
因为g(x0)=-a=0(00).
所以h(x)min=a-a ln a-1≥0,设F(a)=a-a ln a-1(a>0),
因为F′(a)=1-(1+ln a)=-ln a,所以F(a)在(0,1)上单调递增,(1,+∞)上单调递减,
所以F(a)≤F(1)=0,而依题意必有F(a)≥0,所以F(a)=0,此时a=1,
所以若不等式f(x)≥g(x)恒成立,则正实数a的值为1.
(2)证明:方法一 由(1)得,当a=1时,f(x)=xex-(x+ln x)≥1对任意x>0恒成立.
所以 x∈(0,+∞),xex≥x+ln x+1,(当且仅当x=1时等号成立),
则x2ex≥x2+x ln x+x(x>0).
所以要证明x2ex>(x+2)ln x+2sin x(x>0),只需证x2+x ln x+x>(x+2)ln x+2sin x(x>0),
即证x2+x>2ln x+2sin x(x>0).
设β(x)=ln x-x+1,则β′(x)=-1=(x>0),β(x)在(0,1)上单调递增,(1,+∞)上单调递减.
所以 x∈(0,+∞),β(x)≤β(1)=0,即ln x≤x-1(x>0).
所以只需证x2+x>2(x-1)+2sin x,即证x2-x+2>2sin x.
①当x>1时,x2-x+2=x(x-1)+2>2≥2sin x,不等式成立.
②当0所以x2ex≥x2+3x-2>(x+2)ln x+2sin x(x>0).
方法二 设α(x)=x-sin x,则α′(x)=1-cos x≥0恒成立,α(x)在(0,+∞)上单调递增,
x∈(0,+∞),α(x)>α(0)=0,所以x>sin x(x>0).
设β(x)=ln x-x+1,则β′(x)=-1=(x>0),β(x)在(0,1)上单调递增,(1,+∞)上单调递减,
x∈(0,+∞),β(x)≤β(1)=0,所以ln x≤x-1(x>0),所以ln ex≤ex-1,即ex≥x+1.
所以当x∈(0,+∞)时,(x+2)ln x+2sin x<(x+2)(x-1)+2x=x2+3x-2.
又因为x2ex-(x2+3x-2)≥x2(x+1)-[x(x+1)+2(x-1)]=(x-1)2(x+2)≥0,
所以x2ex≥x2+3x-2>(x+2)ln x+2sin x(x>0).
归纳总结
用导数证明不等式的方法
(1)利用单调性:若f(x)在[a,b]上是增函数,则① x∈[a,b],则f(a)≤f(x)≤f(b);②对 x1,x2∈[a,b],且x1(2)利用最值:若f(x)在某个范围D内有最大值M(或最小值m),则对 x∈D,有f(x)≤M(或f(x)≥m).
(3)证明f(x)对点训练
[2021·全国乙卷]设函数f(x)=ln (a-x),已知x=0是函数y=xf(x)的极值点.
(1)求a;
(2)设函数g(x)=,证明:g(x)<1.
解析:(1)由题意得y=xf(x)=x ln (a-x),
则y′=ln (a-x)+x[ln (a-x)]′.
因为x=0是函数y=xf(x)的极值点,
所以y′|x=0=ln a=0,所以a=1.
(2)证明:由(1)可知,f(x)=ln (1-x),其定义域为{x|x<1},
当0当x<0时,ln (1-x)>0,此时xf(x)<0.
易知g(x)的定义域为{x|x<1且x≠0},
故要证g(x)=<1,只需证x+f(x)>xf(x),即证x+ln (1-x)-x ln (1-x)>0.
令1-x=t,则t>0且t≠1,则只需证1-t+ln t-(1-t)ln t>0,即证1-t+t ln t>0.
令h(t)=1-t+t ln t, 则h′(t)=-1+ln t+1=ln t,
所以h(t)在(0,1)上单调递减,在(1,+∞)上单调递增,所以h(t)>h(1)=0,
即g(x)<1成立.
考点三 利用导数解决不等式恒(能)成立问题
考点三 利用导数解决不等式恒(能)成立问题——转化·分离·构造
不等式“恒成立”或“能成立”问题的常用结论
(1)单变量“恒成立”与“能成立”问题的转化策略
①对任意的x∈[m,n],a>f(x)恒成立;对任意的x∈[m,n],a②对任意的x∈[m,n],不等式f(x)>g(x)恒成立 [f(x)-g(x)]min>0;对任意的x∈[m,n],不等式f(x)③若存在x∈[m,n],a>f(x)有解(能成立) ___________;若存在x∈[m,n],a若存在x∈[m,n],a>f(x)无解(不成立) __________.
④若存在x0∈[m,n],使不等式f(x0)>g(x0)成立 f(x)-g(x)>0在[m,n]上有解 ________________.
a[f(x)-g(x)]max<0
a≤f(x)min
[f(x)-g(x)]max>0
(2)双变量“恒成立”与“能成立”问题的转化策略
①若 x1∈D1, x2∈D2,使得f(x1)=g(x2),等价于函数f(x)在D1上的值域A与函数g(x)在D2上的值域B的交集不为空集,即A其等价转化的基本思想是:两个函数有相等的函数值,即它们的________有公共部分.
②对 x1∈D1, x2∈D2,都有f(x1)值域
小于
③对 x1∈D1, x2∈D2,使得f(x1)④若 x1∈D1, x2∈D2,使得f(x1)>g(x2)成立,等价于f(x)max>g(x)min.其等价转化思想是:函数f(x)的某一个函数值大于函数g(x)的某一个函数值,即只要有这样的函数值即可,并不要求________函数值.
所有
所有的
例 3 [2022·吉林延边州教育学院一模]已知函数f(x)=ex+ax(a∈R).
(1)讨论函数f(x)的极值点个数;
(2)若f(x)≥1-ln (x+1)对任意的x∈[0,+∞)恒成立,求实数a的取值范围.
解析: (1)f′(x)=ex+a,
①当a≥0时,f′(x)=ex+a>0,所以f(x)在R上单调递增,无极值.
②当a<0时,令f′(x)=0,得x=ln (-a),
当x∈(-∞,ln (-a))时,f′(x)<0;当x∈(ln (-a),+∞)时,f′(x)>0,
即函数f(x)在(-∞,ln (-a))上单调递减,在(ln (-a),+∞)上单调递增,
此时只有一个极值点,
综上所述,当a≥0时,f(x)在R上无极值点;
当a<0时,函数f(x)在R上只有一个极值点.
(2)若x≥0时, f(x)≥1-ln (x+1),即ex+ax+ln (x+1)-1≥0.(*)
令g(x)=ex+ax+ln (x+1)-1,则g′(x)=ex++a,
令φ(x)=ex++a,则φ′(x)=ex-=≥0,
∴函数φ(x)在区间[0,+∞)上单调递增,φ(0)=2+a,
①若a≥-2,φ(0)=2+a≥0,
∴φ(x)=ex++a≥0,∴g′(x)≥0.
函数g(x)在区间[0,+∞)上单调递增.
∴g(x)≥g(0)=0.∴(*)式成立.
②若a<-2,
由于φ(0)=2+a<0,φ(-a)=e-a++a≥1-a++a=1+>0.
(x≥0 时,ex≥1+x ,故e-a≥1-a )
故 x0∈(0,-a),使得φ(x0)=0,
则当0∴函数g(x)在区间(0,x0)上单调递减,
∴g(x0)综上所述,实数a的取值范围是[-2,+∞).
归纳总结
1.由不等式恒成立求参数的取值范围问题的策略
(1)求最值法:将恒成立问题转化为利用导数求函数的最值问题.
(2)分离参数法:将参数分离出来,进而转化为a>f(x)max或的形式,通过导数的应用求出f(x)的最值,即得参数的范围.
2.不等式能成立问题的解题关键
对点训练
[2022·辽宁一模]已知函数f(x)=x3-x2sin α+x+1,α∈,
(1)讨论函数f(x)的单调性;
(2)证明:存在α∈,使得不等式f(x)>ex 有解(e是自然对数的底数).
解析: (1)f(x) 的定义域为R,f′(x)=x2-2x sin α+1,
Δ=(-2sin α)2-4×=4 ,
①当α∈时,Δ>0 ,f′(x)=0有两个不等实数根为x=,
x∈时,f′(x)>0,f(x)单调递增,
x∈时,
f′(x)<0,f(x)单调递减,
x∈时,f′(x)>0,f(x)单调递增,
②当α∈时,Δ≤0 ,f′(x)≥0,
所以f(x)在(-∞,+∞)上单调递增;
(2)证明:不等式f(x)>ex 等价于(x3-x2sin α+x+1)e-x>1 ,
所以只需证e-x 的最大值大于1,
因为α∈,-1≤-sin α≤,
又x2∈[0,+∞),所以-x2sin α≤x2,α=-时等号成立,
所以e-x≤(x3+x2+x+1)e-x ,
设函数g(x)=e-x ,g′(x)=-x2(x-1)e-x ,
x∈(-∞,1),g′(x)≥0,g(x)单调递增,x∈(1,+∞),g′(x)<0,g(x)单调递减,
因为g(1)==>1 ,所以存在α∈,使不等式f(x)>ex 有解.
[高考5个大题] 解题研诀窍(六) 函数与导数综合问题巧在“转”、难在“分”
[思维流程——找突破口]
[技法指导——迁移搭桥]
函数与导数问题一般以函数为载体,以导数为工具,重点考查函数的一些性质,如含参函数的单调性、极值或最值的探求与讨论,复杂函数零点的讨论,函数不等式中参数范围的讨论,恒成立和能成立问题的讨论等,是近几年高考试题的命题热点.对于这类综合问题,一般是先转化(变形),再求导,分解出基本函数,分类讨论研究其性质,再根据题意解决问题.
[典例] 已知函数f(x)=eln x-ax(a∈R).
(1)讨论f(x)的单调性;
(2)a=e时,证明:xf(x)-ex+2ex≤0.
[快审题]
求什么 想什么 讨论函数的单调性,想到利用导数判断.
证明不等式,想到对所证不等式进行变形转化.
给什么 用什么 已知函数的解析式,利用导数解题.
差什么 找什么 证不等式时,对不等式变形转化后还不能直接判断两函数的关系,应找出所构造函数的最值.
[稳解题]
(1)f′(x)=-a(x>0),
①若a≤0,则f′(x)>0,f(x)在(0,+∞)上单调递增;
②若a>0,则当00,当x>时,f′(x)<0,
故f(x)在上单调递增,在上单调递减.
(2)证明:法一:因为x>0,所以只需证f(x)≤-2e,
当a=e时,由(1)知,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)max=f(1)=-e.
记g(x)=-2e(x>0),
则g′(x)=,
所以当0当x>1时,g′(x)>0,g(x)单调递增,
所以g(x)min=g(1)=-e.
综上,当x>0时,f(x)≤g(x),即f(x)≤-2e,
即xf(x)-ex+2ex≤0.
法二:证xf(x)-ex+2ex≤0,即证ex ln x-ex2-ex+2ex≤0,
从而等价于ln x-x+2≤.
设函数g(x)=ln x-x+2,
则g′(x)=-1.
所以当x∈(0,1)时,g′(x)>0;
当x∈(1,+∞)时,g′(x)<0,故g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,从而g(x)在(0,+∞)上的最大值为g(1)=1.
设函数h(x)=,则h′(x)=.
所以当x∈(0,1)时,h′(x)<0,当x∈(1,+∞)时,h′(x)>0,
故h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
从而h(x)在(0,+∞)上的最小值为h(1)=1.
综上,当x>0时,g(x)≤h(x),即xf(x)-ex+2ex≤0.
题后悟道
函数与导数综合问题的关键
(1)会求函数的极值点,先利用方程f′(x)=0的根,将函数的定义域分成若干个开区间,再列成表格,最后依表格内容即可写出函数的极值;
(2)证明不等式,常构造函数,并利用导数法判断新构造函数的单调性,从而可证明原不等式成立;
(3)不等式恒成立问题除了用分离参数法,还可以从分类讨论和判断函数的单调性入手,去求参数的取值范围.
第4讲 导数的综合应用
考点一
考点二
考点三
考点一
利用导数研究函数的零点
考点一 利用导数研究函数的零点——“形”定个数,“离”参转化
三次函数的零点分布
三次函数在存在两个极值点的情况下,由于当x→∞时,函数值也趋向∞,只要按照极值与零的大小关系确定其零点的个数即可.存在两个极值点x1,x2且x1
a>0(f(x1)为极大值,f(x2)为极小值) 一个 f(x1)<0或f(x2)>0
两个 f(x1)=0或f(x2)=0
三个 f(x1)>0且f(x2)<0
a<0(f(x1)为极小值,f(x2)为极大值) 一个 f(x1)>0或f(x2)<0
两个 f(x1)=0或f(x2)=0
三个 f(x1)<0且f(x2)>0
例 1 [2022·全国乙卷(文)]已知函数f(x)=ax--(a+1)ln x.
(1)当a=0时,求f(x)的最大值;
(2)若f(x)恰有一个零点,求a的取值范围.
解析:(1)当a=0时,f(x)=--ln x(x>0),
则f′(x)==.
当x∈(0,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0.
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故f(x)的最大值即为f(x)的极大值f(1)=-1.
(2)因为函数f(x)恰有一个零点,所以方程a(x-ln x)--ln x=0在(0,+∞)上恰有一个解,即方程a(x-ln x)=+ln x在(0,+∞)上恰有一个解.
又易知当x>0时,x-ln x>0,
所以方程a=在(0,+∞)上恰有一个解.
令g(x)=(x>0),
则g′(x)=.
令h(x)=x-1-(x+1)ln x(x>0),
则h′(x)=1-ln x-=-ln x-.
由(1)知,h′(x)≤-1,
所以h(x)在(0,+∞)上单调递减.
又h(1)=0,所以当x∈(0,1]时,h(x)≥0;
当x∈(1,+∞)时,h(x)<0.
则当x∈(0,1]时,g′(x)≤0;
当x∈(1,+∞)时,g′(x)<0.
所以g(x)在(0,+∞)上单调递减.
又当x→0时,g(x)→+∞,当x→+∞时,g(x)→0,所以a∈(0,+∞).
归纳总结
利用导数研究函数零点问题的思路
(1)构建函数g(x)(要求g′(x)易求,g′(x)=0可解),转化为确定g(x)的零点个数问题求解,利用导数研究该函数的单调性、极值,并确定定义区间端点值的符号(或变化趋势)等,画出g(x)的图象草图,数形结合求解.
(2)利用零点存在性定理:先用该定理判断函数在某区间上有零点,然后利用导数研究函数的单调性、极值(最值)及区间端点值符号,进而判断函数在该区间上零点的个数.
对点训练
[2022·全国乙卷(理)]已知函数f(x)=ln (1+x)+axe-x.
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.
解析:(1)当a=1时,f(x)=ln (1+x)+xe-x,
则f′(x)=,∴f(0)=0,f′(0)=2,
∴曲线y=f(x)在点(0,f(0))处的切线方程为y=2x,即2x-y=0.
(2)方法一 函数f(x)的定义域为(-1,+∞).
①当a≥0时,对于 x>0,f(x)>0,则f(x)在(0,+∞)上不存在零点,故不符合题意.
②当a<0时,f′(x)=+ae-x(1-x)=.
令g(x)=1+ae-x(1-x2),则g′(x)=ae-x(-2x+x2-1)=ae-x(x-1-)(x-1+).
对于 x>-1,e-x>0,∵a<0,∴g(x)在(-1,1-)和(1+,+∞)上单调递减,在(1-,1+)上单调递增.
由已知,得g(-1)=1,g(1-)=1+·2(-1),g(0)=1+a,g(1)=1.
(ⅰ)若-1≤a≤0,则有:
当0
当x>1时,由于1-x2<0,ae-x<0,故g(x)=1+ae-x(1-x2)>1>0.
综上可知,当x>0时,都有g(x)>0,则f′(x)=>0,
∴f(x)在(0,+∞)上单调递增.
∴对于 x>0,f(x)>f(0)=0,f(x)在(0,+∞)上不存在零点,符合题意.
(ⅱ)当a<-1时,g(1-)
且 x∈(-1,x0),都有g(x)>0,则f′(x)=>0,
x∈(x0,0),都有g(x)<0,则f′(x)=<0,
∴f(x)在(-1,x0)上单调递增,在(x0,0)上单调递减.
又∵f(0)=0,∴f(x0)>0.
又∵当x→-1时,f(x)→-∞,
∴f(x)在(-1,0)上恰有一个零点.
∵g(0)=1+a<0,g(1)=1>0,g(x)在(0,1+)上单调递增,在[1+,+∞)上单调递减,
∴ x1∈(0,1),满足g(x1)=0,且当x∈(0,x1)时,g(x)<0,则f′(x)=<0,当x∈(x1,1)时,g(x)>0,则f′(x)=>0.
又∵当x≥1时,ae-x<0,1-x2≤0,
∴g(x)=1+ae-x·(1-x2)>0,∴f′(x)=>0,
∴f(x)在(0,x1)上单调递减,在[x1,+∞)上单调递增.
又∵f(0)=0,∴ x∈(0,x1),f(x)<0,则f(x1)<0.
又∵当x→+∞时,ln (1+x)→+∞,axe-x→0,
∴f(x)→+∞,
∴f(x)在(x1,+∞)上存在零点,且仅有一个.
故f(x)在(0,+∞)上恰有一个零点.
综上可知,满足题意的a的取值范围是(-∞,-1).
方法二 令g(x)=.
f(x)在区间(-1,0),(0,+∞)上各恰有一个零点等价于g(x)==-a在(-1,0),(0,+∞)上各恰有一解.
g′(x)=.
令h(x)=(x-1)ln (1+x)+,
则h′(x)=ln (1+x)+.
令φ(x)=ln (1+x)+,
则φ′(x)=.
①当x∈(0,+∞)时,φ′(x)>0,则h′(x)>h′(0)=0,
∴h(x)>h(0)=0,∴g′(x)>0,∴g(x)在(0,+∞)上单调递增.
又∵当x→0时,g(x)==1,当x→+∞时,g(x)→+∞,∴a∈(-∞,-1).
②当x∈(-1,-2)时,φ′(x)<0;当x∈(-2,0)时,φ′(x)>0.
∵当x→-1时,φ(x)=h′(x)→+∞,h′(0)=0,
∴存在a1∈(-1,0)使h′(a1)=0,
∴h(x)在(-1,a1)上单调递增,在(a1,0)上单调递减.
当x→-1时,h(x)→-∞.
又h(0)=0,
∴存在a2∈(-1,a1),使得h(a2)=0,
即g(x)在(-1,a2)上单调递减,在(a2,0)上单调递增.
当x→-1时,g(x)→+∞;
当x→0时,g(x)→1,g(x)的大致图象如图.
故当a∈(-∞,-1)时,
g(x)=-a仅有一解;
当a∈(-1,-g(a2))时,g(x)=-a有两解.
综上可知,a∈(-∞,-1).
考点二
利用导数证明不等式
考点二 利用导数证明不等式——构造·分离·放缩
常见的指数、对数不等式
(1)ex≥x+1及其变形ex-1≥x,ex≥ex等.
(2)ln x≤x-1(x>0)及其变式ln (x+1)≤x,ln x≥1-等.
例 2 [2022·湖北二模]已知函数f(x)=xex-1,g(x)=a(ln x+x).
(1)若不等式f(x)≥g(x)恒成立,求正实数a的值;
(2)证明:x2ex>(x+2)ln x+2sin x.
解析: (1)令h(x)=f(x)-g(x)=xex-a(ln x+x)-1,
则h′(x)=(x+1)ex-a=(x>0),
设φ(x)=xex-a(a>0),则φ′(x)=(x+1)ex>0对任意x>0恒成立,
所以φ(x)在(0,+∞)上单调递增,
又φ(0)=-a<0,φ(a)=aea-a=a(ea-1)>0,存在唯一实数x0∈(0,a),φ(x0)=0,
所以当x∈(0,x0)时,h′(x)=<0,h(x)单调递减;
当x∈(x0,+∞)时,h′(x)=>0,h(x)单调递增;
所以h(x)min=h(x0)=-a(x0+ln x0)-1.
因为g(x0)=-a=0(0
所以h(x)min=a-a ln a-1≥0,设F(a)=a-a ln a-1(a>0),
因为F′(a)=1-(1+ln a)=-ln a,所以F(a)在(0,1)上单调递增,(1,+∞)上单调递减,
所以F(a)≤F(1)=0,而依题意必有F(a)≥0,所以F(a)=0,此时a=1,
所以若不等式f(x)≥g(x)恒成立,则正实数a的值为1.
(2)证明:方法一 由(1)得,当a=1时,f(x)=xex-(x+ln x)≥1对任意x>0恒成立.
所以 x∈(0,+∞),xex≥x+ln x+1,(当且仅当x=1时等号成立),
则x2ex≥x2+x ln x+x(x>0).
所以要证明x2ex>(x+2)ln x+2sin x(x>0),只需证x2+x ln x+x>(x+2)ln x+2sin x(x>0),
即证x2+x>2ln x+2sin x(x>0).
设β(x)=ln x-x+1,则β′(x)=-1=(x>0),β(x)在(0,1)上单调递增,(1,+∞)上单调递减.
所以 x∈(0,+∞),β(x)≤β(1)=0,即ln x≤x-1(x>0).
所以只需证x2+x>2(x-1)+2sin x,即证x2-x+2>2sin x.
①当x>1时,x2-x+2=x(x-1)+2>2≥2sin x,不等式成立.
②当0
方法二 设α(x)=x-sin x,则α′(x)=1-cos x≥0恒成立,α(x)在(0,+∞)上单调递增,
x∈(0,+∞),α(x)>α(0)=0,所以x>sin x(x>0).
设β(x)=ln x-x+1,则β′(x)=-1=(x>0),β(x)在(0,1)上单调递增,(1,+∞)上单调递减,
x∈(0,+∞),β(x)≤β(1)=0,所以ln x≤x-1(x>0),所以ln ex≤ex-1,即ex≥x+1.
所以当x∈(0,+∞)时,(x+2)ln x+2sin x<(x+2)(x-1)+2x=x2+3x-2.
又因为x2ex-(x2+3x-2)≥x2(x+1)-[x(x+1)+2(x-1)]=(x-1)2(x+2)≥0,
所以x2ex≥x2+3x-2>(x+2)ln x+2sin x(x>0).
归纳总结
用导数证明不等式的方法
(1)利用单调性:若f(x)在[a,b]上是增函数,则① x∈[a,b],则f(a)≤f(x)≤f(b);②对 x1,x2∈[a,b],且x1
(3)证明f(x)
[2021·全国乙卷]设函数f(x)=ln (a-x),已知x=0是函数y=xf(x)的极值点.
(1)求a;
(2)设函数g(x)=,证明:g(x)<1.
解析:(1)由题意得y=xf(x)=x ln (a-x),
则y′=ln (a-x)+x[ln (a-x)]′.
因为x=0是函数y=xf(x)的极值点,
所以y′|x=0=ln a=0,所以a=1.
(2)证明:由(1)可知,f(x)=ln (1-x),其定义域为{x|x<1},
当0
易知g(x)的定义域为{x|x<1且x≠0},
故要证g(x)=<1,只需证x+f(x)>xf(x),即证x+ln (1-x)-x ln (1-x)>0.
令1-x=t,则t>0且t≠1,则只需证1-t+ln t-(1-t)ln t>0,即证1-t+t ln t>0.
令h(t)=1-t+t ln t, 则h′(t)=-1+ln t+1=ln t,
所以h(t)在(0,1)上单调递减,在(1,+∞)上单调递增,所以h(t)>h(1)=0,
即g(x)<1成立.
考点三 利用导数解决不等式恒(能)成立问题
考点三 利用导数解决不等式恒(能)成立问题——转化·分离·构造
不等式“恒成立”或“能成立”问题的常用结论
(1)单变量“恒成立”与“能成立”问题的转化策略
①对任意的x∈[m,n],a>f(x)恒成立;对任意的x∈[m,n],a
④若存在x0∈[m,n],使不等式f(x0)>g(x0)成立 f(x)-g(x)>0在[m,n]上有解 ________________.
a
a≤f(x)min
[f(x)-g(x)]max>0
(2)双变量“恒成立”与“能成立”问题的转化策略
①若 x1∈D1, x2∈D2,使得f(x1)=g(x2),等价于函数f(x)在D1上的值域A与函数g(x)在D2上的值域B的交集不为空集,即A其等价转化的基本思想是:两个函数有相等的函数值,即它们的________有公共部分.
②对 x1∈D1, x2∈D2,都有f(x1)
小于
③对 x1∈D1, x2∈D2,使得f(x1)
所有
所有的
例 3 [2022·吉林延边州教育学院一模]已知函数f(x)=ex+ax(a∈R).
(1)讨论函数f(x)的极值点个数;
(2)若f(x)≥1-ln (x+1)对任意的x∈[0,+∞)恒成立,求实数a的取值范围.
解析: (1)f′(x)=ex+a,
①当a≥0时,f′(x)=ex+a>0,所以f(x)在R上单调递增,无极值.
②当a<0时,令f′(x)=0,得x=ln (-a),
当x∈(-∞,ln (-a))时,f′(x)<0;当x∈(ln (-a),+∞)时,f′(x)>0,
即函数f(x)在(-∞,ln (-a))上单调递减,在(ln (-a),+∞)上单调递增,
此时只有一个极值点,
综上所述,当a≥0时,f(x)在R上无极值点;
当a<0时,函数f(x)在R上只有一个极值点.
(2)若x≥0时, f(x)≥1-ln (x+1),即ex+ax+ln (x+1)-1≥0.(*)
令g(x)=ex+ax+ln (x+1)-1,则g′(x)=ex++a,
令φ(x)=ex++a,则φ′(x)=ex-=≥0,
∴函数φ(x)在区间[0,+∞)上单调递增,φ(0)=2+a,
①若a≥-2,φ(0)=2+a≥0,
∴φ(x)=ex++a≥0,∴g′(x)≥0.
函数g(x)在区间[0,+∞)上单调递增.
∴g(x)≥g(0)=0.∴(*)式成立.
②若a<-2,
由于φ(0)=2+a<0,φ(-a)=e-a++a≥1-a++a=1+>0.
(x≥0 时,ex≥1+x ,故e-a≥1-a )
故 x0∈(0,-a),使得φ(x0)=0,
则当0
∴g(x0)
归纳总结
1.由不等式恒成立求参数的取值范围问题的策略
(1)求最值法:将恒成立问题转化为利用导数求函数的最值问题.
(2)分离参数法:将参数分离出来,进而转化为a>f(x)max或的形式,通过导数的应用求出f(x)的最值,即得参数的范围.
2.不等式能成立问题的解题关键
对点训练
[2022·辽宁一模]已知函数f(x)=x3-x2sin α+x+1,α∈,
(1)讨论函数f(x)的单调性;
(2)证明:存在α∈,使得不等式f(x)>ex 有解(e是自然对数的底数).
解析: (1)f(x) 的定义域为R,f′(x)=x2-2x sin α+1,
Δ=(-2sin α)2-4×=4 ,
①当α∈时,Δ>0 ,f′(x)=0有两个不等实数根为x=,
x∈时,f′(x)>0,f(x)单调递增,
x∈时,
f′(x)<0,f(x)单调递减,
x∈时,f′(x)>0,f(x)单调递增,
②当α∈时,Δ≤0 ,f′(x)≥0,
所以f(x)在(-∞,+∞)上单调递增;
(2)证明:不等式f(x)>ex 等价于(x3-x2sin α+x+1)e-x>1 ,
所以只需证e-x 的最大值大于1,
因为α∈,-1≤-sin α≤,
又x2∈[0,+∞),所以-x2sin α≤x2,α=-时等号成立,
所以e-x≤(x3+x2+x+1)e-x ,
设函数g(x)=e-x ,g′(x)=-x2(x-1)e-x ,
x∈(-∞,1),g′(x)≥0,g(x)单调递增,x∈(1,+∞),g′(x)<0,g(x)单调递减,
因为g(1)==>1 ,所以存在α∈,使不等式f(x)>ex 有解.
[高考5个大题] 解题研诀窍(六) 函数与导数综合问题巧在“转”、难在“分”
[思维流程——找突破口]
[技法指导——迁移搭桥]
函数与导数问题一般以函数为载体,以导数为工具,重点考查函数的一些性质,如含参函数的单调性、极值或最值的探求与讨论,复杂函数零点的讨论,函数不等式中参数范围的讨论,恒成立和能成立问题的讨论等,是近几年高考试题的命题热点.对于这类综合问题,一般是先转化(变形),再求导,分解出基本函数,分类讨论研究其性质,再根据题意解决问题.
[典例] 已知函数f(x)=eln x-ax(a∈R).
(1)讨论f(x)的单调性;
(2)a=e时,证明:xf(x)-ex+2ex≤0.
[快审题]
求什么 想什么 讨论函数的单调性,想到利用导数判断.
证明不等式,想到对所证不等式进行变形转化.
给什么 用什么 已知函数的解析式,利用导数解题.
差什么 找什么 证不等式时,对不等式变形转化后还不能直接判断两函数的关系,应找出所构造函数的最值.
[稳解题]
(1)f′(x)=-a(x>0),
①若a≤0,则f′(x)>0,f(x)在(0,+∞)上单调递增;
②若a>0,则当0
故f(x)在上单调递增,在上单调递减.
(2)证明:法一:因为x>0,所以只需证f(x)≤-2e,
当a=e时,由(1)知,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)max=f(1)=-e.
记g(x)=-2e(x>0),
则g′(x)=,
所以当0
所以g(x)min=g(1)=-e.
综上,当x>0时,f(x)≤g(x),即f(x)≤-2e,
即xf(x)-ex+2ex≤0.
法二:证xf(x)-ex+2ex≤0,即证ex ln x-ex2-ex+2ex≤0,
从而等价于ln x-x+2≤.
设函数g(x)=ln x-x+2,
则g′(x)=-1.
所以当x∈(0,1)时,g′(x)>0;
当x∈(1,+∞)时,g′(x)<0,故g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,从而g(x)在(0,+∞)上的最大值为g(1)=1.
设函数h(x)=,则h′(x)=.
所以当x∈(0,1)时,h′(x)<0,当x∈(1,+∞)时,h′(x)>0,
故h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
从而h(x)在(0,+∞)上的最小值为h(1)=1.
综上,当x>0时,g(x)≤h(x),即xf(x)-ex+2ex≤0.
题后悟道
函数与导数综合问题的关键
(1)会求函数的极值点,先利用方程f′(x)=0的根,将函数的定义域分成若干个开区间,再列成表格,最后依表格内容即可写出函数的极值;
(2)证明不等式,常构造函数,并利用导数法判断新构造函数的单调性,从而可证明原不等式成立;
(3)不等式恒成立问题除了用分离参数法,还可以从分类讨论和判断函数的单调性入手,去求参数的取值范围.
同课章节目录
