(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题三 立体几何 第1讲 空间几何体的三视图、表面积与体积 课件(32张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题三 立体几何 第1讲 空间几何体的三视图、表面积与体积 课件(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
第1讲 空间几何体的三视图、表面积与体积
考点一
考点二
考点三
考点一
空间几何体的三视图
考点一 空间几何体的三视图——识图、想图、构图,“原形毕露”
一个物体的三视图的排列规则
俯视图放在正视图的下面,长度与正视图的长度一样;侧视图放在正视图的右面,高度与正视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.
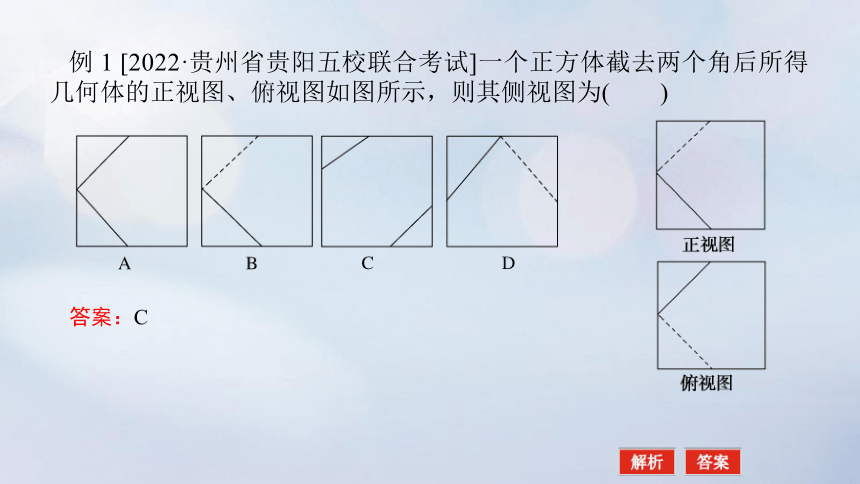
例 1 [2022·贵州省贵阳五校联合考试]一个正方体截去两个角后所得几何体的正视图、俯视图如图所示,则其侧视图为( )
答案:C
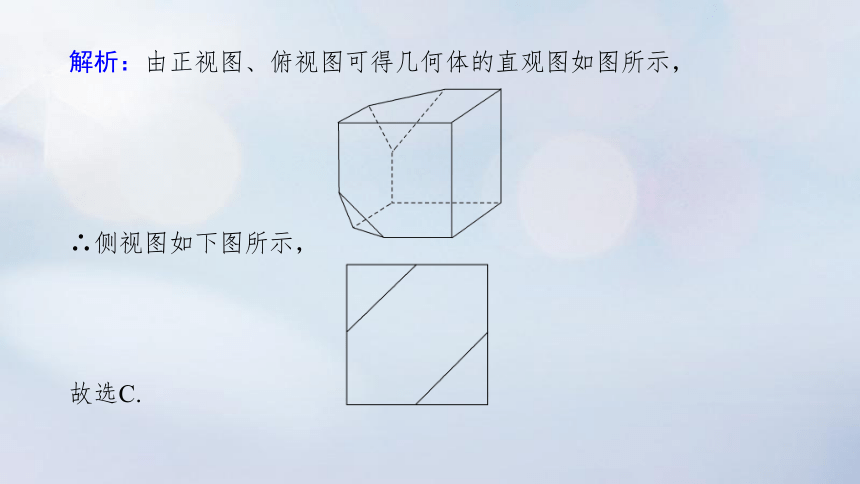
解析:由正视图、俯视图可得几何体的直观图如图所示,
∴侧视图如下图所示,
故选C.
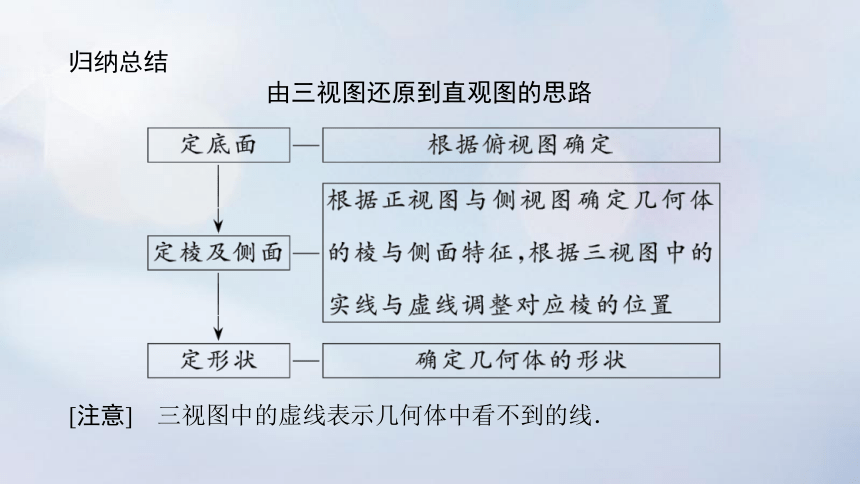
归纳总结
由三视图还原到直观图的思路
[注意] 三视图中的虚线表示几何体中看不到的线.
对点训练
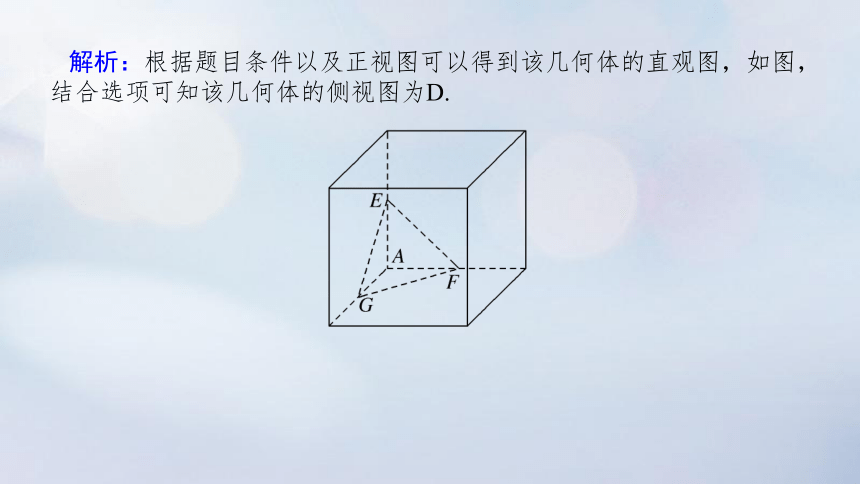
[2021·全国甲卷]在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
答案:D
解析:根据题目条件以及正视图可以得到该几何体的直观图,如图,结合选项可知该几何体的侧视图为D.
考点二
空间几何体的表面积与体积
考点二 空间几何体的表面积与体积——找特征、求标量、代公式,割补相济
1.柱体、锥体、台体的侧面积公式
(1)S直棱柱侧=________(c为底面周长,h为高);
(2)S正棱锥侧=______(c为底面周长,h′为斜高);
(3)S正棱台侧=________(c′,c分别为上、下底面的周长,h′为斜高).
ch
ch′
(c+c′)h′
2.柱体、锥体、台体的体积公式
(1)V柱体=________(S为底面面积,h为高),
(2)V锥体=________(S为底面面积,h为高);
(3)V台体=_____________ (S,S′分别为上、下底面面积,h为高).
3.球的表面积和体积公式
(1)S球表=________(R为球的半径);
(2)V球=________(R为球的半径).
Sh
Sh
(S++S′)h
4πR2
πR3
角度 1 求空间几何体的表面积
例 2 [2021·北京卷]某四面体的三视图如图所示,该四面体的表面积为( )
A. B.4
C.3+ D.2
答案:A
解析:根据三视图可得如图所示的几何体正三棱锥O ABC,
其侧面为等腰直角三角形,底面为等边三角形,
由三视图可得该正三棱锥的侧棱长为1,
故其表面积为3××1×1+2=,
故选A.
归纳总结
求多面体的表面积 只需将它们沿着棱“剪开”并展成平面图形,利用求平面图形面积的方法求多面体的表面积
求旋转体的表面积 可以从旋转体的形成过程及其结构特征入手,将其展开后求表面积,但要搞清楚它们的底面半径、母线长与对应侧面展开图中的边长关系
求不规则几何体的表面积 通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积
角度2 求空间几何体的体积
例 3 [2022·全国甲卷]如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )
A.8 B.12 C.16 D.20
答案:B
解析:如图,将三视图还原成直观图.该直观图是一个侧放的直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=2,AB=4,AA1=2.所以底面面积S==6,设该直四棱柱的高为h,则该几何体的体积V=Sh=6×2=12.故选B.
归纳总结
求空间几何体体积的常用方法
公式法 直接根据常见柱、锥、台等规则几何体的体积公式计算
等积法 根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等
割补法 把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体
对点训练
1.[2022·浙江湖州模拟预测]如图,某多面体的体积是,其三视图如图所示,则正视图中的高a=( )
A.1 B. C. D.
答案:B
解析:由三视图还原出原几何体为三棱锥,如图所示,
结合三视图得该三棱锥体积为:V=×2×2×a=,所以a=.故选B.
2.[2022·浙江三模]某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A. B.2 C.3 D.
答案:C
解析:从三视图可以得到直观图为直六棱柱,如图所示,
在俯视图中,可以求出底面积为S=2××1×1+=3,从正视图和侧视图可知直六棱柱的高为1,所以该几何体的体积是V=3×1=3.故选C.
考点三
多面体与球的切、接问题
考点三 多面体与球的切、接问题——找“切”点,抓“接”点,与半径相“联”
几何体与球组合体的结论
(1)正方体的棱长为a,球的半径为R.
①正方体的外接球,则2R=a;
②正方体的内切球,则2R=a;
③球与正方体的各棱相切,则2R=a.
(2)在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=.
(3)正四面体的外接球与内切球的半径之比为3∶1.
例 4 (1)[2022·新高考Ⅱ卷]已知正三棱台的高为1,上、下底面边长分别为3和4,其顶点都在同一球面上,则该球的表面积为( )
A.100π B.128π
C.144π D.192π
答案:A
解析:设三棱台上底面A1B1C1、下底面ABC的外接圆半径分别为r1,r2,外接圆圆心分别为O1,O2,三棱台的外接球半径为R,球心为O.令|OO1|=t,则|OO2|=|t-1|.由题意及正弦定理,得2r1==6,2r2==8,所以r1=3,r2=4,所以R2=+t2=+(t-1)2,即R2=9+t2=16+(t-1)2,解得所以三棱台外接球的表面积为4πR2=100π.故选A.
(2)[2022·四川省内江市第六中学模拟]已知正四棱锥的侧棱长为,底面边长为2,则该四棱锥的内切球的体积为( )
A. B.
C. D.4
答案:B
解析:如图,设O为正四棱锥的底面中心,E为BC的中点,连接PO,OE,PE,
则PO为四棱锥的高,PE为侧面三角形PBC的高,
因为BC=2,PB=,故PE==2 ,则PO== ,
设该四棱锥的内切球的半径为r,
则·S正方形ABCD·PO=(S正方形ABCD+4S△PBC)r ,
即×4×=(4+4××2×2)×r ,解得r= ,
故内切球的体积为V=π×3= ,故选B.
归纳总结
空间几何体与球接、切问题的求解方法
(1)确定球心的位置,弄清球的半径(直径)与几何体的位置和数量关系.
(2)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(3)补成正方体、长方体、正四面体、正棱柱、圆柱等规则的几何体.
提醒 内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.这也是解决此类问题的易错点.
对点训练
1.[2022·青海海东市第一中学检测]已知在三棱锥P ABC中,PA=4,BC=2,PB=PC=3,PA⊥平面PBC,则三棱锥P ABC的外接球的表面积是________.
43π
解析:在等腰△PBC中,易知cos ∠PBC=,所以sin ∠PBC=,△PBC的外接圆的半径为r==,所以三棱锥P ABC的外接球的半径为R== =.
所以其表面积为4πR2=4π2=43π.
2.[2021·全国甲卷]已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O ABC的体积为( )
A. B. C. D.
答案:A
解析:如图所示,因为AC⊥BC,且AC=BC=1,所以AB为截面圆O1的直径,且AB=.连接OO1,则OO1⊥平面ABC,OO1===,所以三棱锥O ABC的体积V=×OO1=×1×1×=.故选A.
第1讲 空间几何体的三视图、表面积与体积
考点一
考点二
考点三
考点一
空间几何体的三视图
考点一 空间几何体的三视图——识图、想图、构图,“原形毕露”
一个物体的三视图的排列规则
俯视图放在正视图的下面,长度与正视图的长度一样;侧视图放在正视图的右面,高度与正视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.
例 1 [2022·贵州省贵阳五校联合考试]一个正方体截去两个角后所得几何体的正视图、俯视图如图所示,则其侧视图为( )
答案:C
解析:由正视图、俯视图可得几何体的直观图如图所示,
∴侧视图如下图所示,
故选C.
归纳总结
由三视图还原到直观图的思路
[注意] 三视图中的虚线表示几何体中看不到的线.
对点训练
[2021·全国甲卷]在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
答案:D
解析:根据题目条件以及正视图可以得到该几何体的直观图,如图,结合选项可知该几何体的侧视图为D.
考点二
空间几何体的表面积与体积
考点二 空间几何体的表面积与体积——找特征、求标量、代公式,割补相济
1.柱体、锥体、台体的侧面积公式
(1)S直棱柱侧=________(c为底面周长,h为高);
(2)S正棱锥侧=______(c为底面周长,h′为斜高);
(3)S正棱台侧=________(c′,c分别为上、下底面的周长,h′为斜高).
ch
ch′
(c+c′)h′
2.柱体、锥体、台体的体积公式
(1)V柱体=________(S为底面面积,h为高),
(2)V锥体=________(S为底面面积,h为高);
(3)V台体=_____________ (S,S′分别为上、下底面面积,h为高).
3.球的表面积和体积公式
(1)S球表=________(R为球的半径);
(2)V球=________(R为球的半径).
Sh
Sh
(S++S′)h
4πR2
πR3
角度 1 求空间几何体的表面积
例 2 [2021·北京卷]某四面体的三视图如图所示,该四面体的表面积为( )
A. B.4
C.3+ D.2
答案:A
解析:根据三视图可得如图所示的几何体正三棱锥O ABC,
其侧面为等腰直角三角形,底面为等边三角形,
由三视图可得该正三棱锥的侧棱长为1,
故其表面积为3××1×1+2=,
故选A.
归纳总结
求多面体的表面积 只需将它们沿着棱“剪开”并展成平面图形,利用求平面图形面积的方法求多面体的表面积
求旋转体的表面积 可以从旋转体的形成过程及其结构特征入手,将其展开后求表面积,但要搞清楚它们的底面半径、母线长与对应侧面展开图中的边长关系
求不规则几何体的表面积 通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积
角度2 求空间几何体的体积
例 3 [2022·全国甲卷]如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )
A.8 B.12 C.16 D.20
答案:B
解析:如图,将三视图还原成直观图.该直观图是一个侧放的直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=2,AB=4,AA1=2.所以底面面积S==6,设该直四棱柱的高为h,则该几何体的体积V=Sh=6×2=12.故选B.
归纳总结
求空间几何体体积的常用方法
公式法 直接根据常见柱、锥、台等规则几何体的体积公式计算
等积法 根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等
割补法 把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体
对点训练
1.[2022·浙江湖州模拟预测]如图,某多面体的体积是,其三视图如图所示,则正视图中的高a=( )
A.1 B. C. D.
答案:B
解析:由三视图还原出原几何体为三棱锥,如图所示,
结合三视图得该三棱锥体积为:V=×2×2×a=,所以a=.故选B.
2.[2022·浙江三模]某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A. B.2 C.3 D.
答案:C
解析:从三视图可以得到直观图为直六棱柱,如图所示,
在俯视图中,可以求出底面积为S=2××1×1+=3,从正视图和侧视图可知直六棱柱的高为1,所以该几何体的体积是V=3×1=3.故选C.
考点三
多面体与球的切、接问题
考点三 多面体与球的切、接问题——找“切”点,抓“接”点,与半径相“联”
几何体与球组合体的结论
(1)正方体的棱长为a,球的半径为R.
①正方体的外接球,则2R=a;
②正方体的内切球,则2R=a;
③球与正方体的各棱相切,则2R=a.
(2)在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=.
(3)正四面体的外接球与内切球的半径之比为3∶1.
例 4 (1)[2022·新高考Ⅱ卷]已知正三棱台的高为1,上、下底面边长分别为3和4,其顶点都在同一球面上,则该球的表面积为( )
A.100π B.128π
C.144π D.192π
答案:A
解析:设三棱台上底面A1B1C1、下底面ABC的外接圆半径分别为r1,r2,外接圆圆心分别为O1,O2,三棱台的外接球半径为R,球心为O.令|OO1|=t,则|OO2|=|t-1|.由题意及正弦定理,得2r1==6,2r2==8,所以r1=3,r2=4,所以R2=+t2=+(t-1)2,即R2=9+t2=16+(t-1)2,解得所以三棱台外接球的表面积为4πR2=100π.故选A.
(2)[2022·四川省内江市第六中学模拟]已知正四棱锥的侧棱长为,底面边长为2,则该四棱锥的内切球的体积为( )
A. B.
C. D.4
答案:B
解析:如图,设O为正四棱锥的底面中心,E为BC的中点,连接PO,OE,PE,
则PO为四棱锥的高,PE为侧面三角形PBC的高,
因为BC=2,PB=,故PE==2 ,则PO== ,
设该四棱锥的内切球的半径为r,
则·S正方形ABCD·PO=(S正方形ABCD+4S△PBC)r ,
即×4×=(4+4××2×2)×r ,解得r= ,
故内切球的体积为V=π×3= ,故选B.
归纳总结
空间几何体与球接、切问题的求解方法
(1)确定球心的位置,弄清球的半径(直径)与几何体的位置和数量关系.
(2)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(3)补成正方体、长方体、正四面体、正棱柱、圆柱等规则的几何体.
提醒 内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.这也是解决此类问题的易错点.
对点训练
1.[2022·青海海东市第一中学检测]已知在三棱锥P ABC中,PA=4,BC=2,PB=PC=3,PA⊥平面PBC,则三棱锥P ABC的外接球的表面积是________.
43π
解析:在等腰△PBC中,易知cos ∠PBC=,所以sin ∠PBC=,△PBC的外接圆的半径为r==,所以三棱锥P ABC的外接球的半径为R== =.
所以其表面积为4πR2=4π2=43π.
2.[2021·全国甲卷]已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O ABC的体积为( )
A. B. C. D.
答案:A
解析:如图所示,因为AC⊥BC,且AC=BC=1,所以AB为截面圆O1的直径,且AB=.连接OO1,则OO1⊥平面ABC,OO1===,所以三棱锥O ABC的体积V=×OO1=×1×1×=.故选A.
同课章节目录
