(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题三 立体几何 第3讲 空间向量与立体几何 课件(48张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题三 立体几何 第3讲 空间向量与立体几何 课件(48张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 05:58:27 | ||
图片预览











文档简介
(共48张PPT)
第3讲 空间向量与立体几何
考点一
考点二
考点三
考点一
向量法证明平行与垂直
考点一 向量法证明平行与垂直——建系,找点,写向量;平行,垂直,找关系
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2).
平面α,β的法向量分别为u=(a3,b3,c3),v=(a4,b4,c4).
(1)l∥m a∥b a=kb a1=______,b1=______,c1=______;
(2)l⊥m a⊥b a·b=______ a1a2+b1b2+c1c2=______;
(3)l∥α a⊥u a·u=______ a1a3+b1b3+c1c3=______;
(4)l⊥α a∥u a=ku a1=______,b1=______,c1=_____;
(5)α∥β u∥v u=kv a3=______,b3=______,c3=______;
(6)α⊥β u⊥v u·v=0 a3a4+b3b4+c3c4=______.
ka2
kb2
kc2
0
0
0
0
ka3
kb3
kc3
ka4
kb4
kc4
0
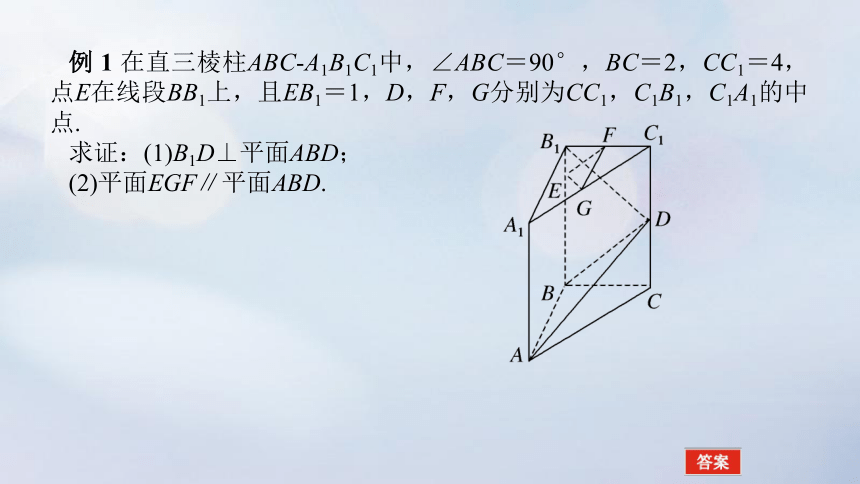
例 1 在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.
求证:(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
证明:(1)以B为坐标原点,BA,BC,BB1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系B-xyz,如图所示,
则B(0,0,0),D(0,2,2),B1(0,0,4),设BA=a,则A(a,0,0),
所以=(a,0,0),=(0,2,2),=(0,2,-2),
·=0,·=0+4-4=0,
即B1D⊥BA,B1D⊥BD.
又因为BA=B,BA,BD 平面ABD,
因此B1D⊥平面ABD.
(2)由(1)知,E(0,0,3),G,F(0,1,4),
则==(0,1,1),
·=0+2-2=0,·=0+2-2=0,
即B1D⊥EG,B1D⊥EF.
又因为EG=E,EG,EF 平面EGF,因此B1D⊥平面EGF.
结合(1)可知平面EGF∥平面ABD.
归纳总结
利用空间向量证明平行与垂直的步骤
(1)建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系;
(2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面中的要素;
(3)通过空间向量的运算研究平行、垂直关系;
(4)根据运算结果解释相关问题.
对点训练
如图,在直三棱柱ADE-BCF中,平面ABFE和平面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运用向量方法证明:
(1)OM∥平面BCF;
(2)平面MDF⊥平面EFCD.
证明:由题意得AB,AD,AE两两垂直,以A为坐标原点建立如图所示的空间直角坐标系A-xyz.
设正方形边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),
F(1,0,1),M,
O.
(1)=,
=(-1,0,0),
所以·=0,所以⊥.
因为棱柱ADE BCF是直三棱柱,所以AB⊥平面BCF,所以是平面BCF的一个法向量,且OM 平面BCF,所以OM∥平面BCF.
(2)设平面MDF与平面EFCD的一个法向量分别为n1=(x1,y1,z1),n2=(x2,y2,z2).
因为=(1,-1,1),==(1,0,0),=(0,-1,1),
由n1·=n1·=0,得
解得令x1=1,则n1=.
同理可得n2=(0,1,1).
因为n1·n2=0,所以平面MDF⊥平面EFCD.
考点二 向量法求空间角
考点二 向量法求空间角——巧妙建系,求向量夹角
向量法求异面直线所成的角
若异面直线a,b的方向向量分别为a,b,异面直线所成的角为θ,则cos θ=|cos 〈a,b〉|=.
2.向量法求线面所成的角
求出平面的法向量n,直线的方向向量a,设线面所成的角为θ,则sin θ=|cos 〈n,a〉|=.
3.向量法求二面角
求出二面角α l β的两个半平面α与β的法向量n1,n2,若二面角α l β所成的角θ为锐角,则cos θ=|cos 〈n1,n2〉|=;若二面角α l β所成的角θ为钝角,则cos θ=-|cos 〈n1,n2〉|=-.
例 2 [2022·全国乙卷理]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
解析:(1)证明:∵AD=CD,∠ADB=∠BDC,BD=BD,
∴△ABD≌△CBD,∴AB=CB.
∵E为AC的中点,∴DE⊥AC,BE⊥AC.
∵DE=E,DE,BE 平面BED,
∴AC⊥平面BED.
∵AC 平面ACD,∴平面BED⊥平面ACD.
(2)如图,连接EF.由(1)知AC⊥平面BED.
又∵EF 平面BED,
∴EF⊥AC.
∴S△AFC=AC·EF.
当EF⊥BD时,EF的长最小,此时△AFC的面积最小.
由(1)知AB=CB=2.
又∵∠ACB=60°,
∴△ABC是边长为2的正三角形,∴BE=.
∵AD⊥CD,∴DE=1,
∴DE2+BE2=BD2,∴DE⊥BE.
以点E为坐标原点,直线EA ,EB ,ED分别为x轴、y轴、z轴建立空间直角坐标系,则E(0,0,0),A(1,0,0),B(0,,0),C(-1,0,0),D(0,0,1),
∴=(-1,,0),=(-1,0,1),=(0,,-1),=(0,0,1),=(-1,0,0).
设=λ(0≤λ≤1),
则==+λ=(0,0,1)+λ(0,,-1)=(0,λ,1-λ).
∵EF⊥DB,∴·=(0,λ,1-λ)·(0,,-1)=4λ-1=0,
∴λ=,∴=(0,),∴==(0,)-(-1,0,0)=(1,).
设平面ABD的法向量为n=(x,y,z),
则即
取y=1,则x=,z=,∴n=(,1,).
设当△AFC的面积最小时,CF与平面ABD所成的角为θ,则sin θ=|cos 〈n,〉|===.
故当△AFC的面积最小时,CF与平面ABD所成的角的正弦值为.
归纳总结
1.利用向量法求线面角的方法
(1)分别求出斜线和它在平面内的射影的方向向量,转化为求两个方向向量的夹角(或其补角);
(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(或钝角的补角),取其余角就是斜线和平面所成的角.即线面角的正弦值等于斜线的方向向量与平面的法向量夹角余弦值的绝对值.
2.利用向量法求二面角的方法
(1)分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的大小;
(2)通过平面的法向量来求:设二面角的两个半平面的法向量分别为n1和n2,则二面角的大小等于〈n1,n2〉(或π-〈n1,n2〉).
提醒
求空间角注意:①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|.②两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角.③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值,即注意函数名称的变化.
对点训练
[2021·全国乙卷改编]如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.
(1)求BC;
(2)求二面角A-PM B的正弦值;
(3)求直线PB与CD所成的角;
(4)求直线PB与平面PAM所成角的正弦值.
解析:(1)因为PD⊥平面ABCD,所以PD⊥AD,PD⊥DC.
在矩形ABCD中,AD⊥DC,故以点D为坐标原点建立空间直角坐标系如图所示,
设BC=t,则A(t,0,0),B(t,1,0),M,P(0,0,1),
所以=(t,1,-1),=.
因为PB⊥AM,所以·=-+1=0,得t=,
所以BC=.
(2)易知C(0,1,0),由(1)可得=(-,0,1),==(,0,0),=(,1,-1).
设平面APM的法向量为n1=(x1,y1,z1),则
,即,
令x1=,则z1=2,y1=1,所以平面APM的一个法向量n1=(,1,2).
设平面PMB的法向量为n2=(x2,y2,z2),则
,即,
得x2=0,令y2=1,则z2=1,所以平面PMB的一个法向量为n2=(0,1,1).
cos 〈n1,n2〉===,
所以二面角A PM B的正弦值为.
(3)由题意知:
P(0,0,1),B(,1,0),C(0,1,0),D(0,0,0),则=(0,1,0),=(,1,-1),设直线PB与CD所成角的大小为θ,
则cos θ=|cos 〈〉|===.
又因为θ∈,
所以θ=,
即直线PB与CD所成的角为.
(4)由题意知:P(0,0,1),B(,1,0),A(,0,0),M.
则=(,1,-1),=.=.
设n=(x,y,z)为平面PAM的法向量,
则即
令x=2,则y=,z=2.所以n=(2,,2).
设直线PB与平面PAM所成角的大小为θ,则
sin θ=|cos 〈,n〉|===,
即直线PB与平面PAM所成角的正弦值为.
考点三
用向量法解决探索性问题
考点三 用向量法解决探索性问题——问题坐标化,探求方程解
与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
例 3 [2022·河北深州市高三期末]如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,BC⊥BB1,CC1=,AC1=.
(1)证明:平面ABC⊥平面BB1C1C;
(2)M,N分别是BC,B1C1的中点,P是线段AC1上的动点,若二面角P MN C的平面角的大小为30°,试确定点P的位置.
解析:(1)证明:因为AC=2,CC1=,AC1=,
所以=,即AC⊥CC1.
又因为BC⊥BB1,BB1∥CC1,所以BC⊥CC1,
AC=C,所以CC1⊥平面ABC.
因为CC1 平面BB1C1C,所以平面ABC⊥平面BB1C1C.
(2)连接AM,因为AB=AC=2,M是BC的中点,所以AM⊥BC.
由(1)知,平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC,所以AM⊥平面BB1C1C.
以M为原点建立如图所示的空间直角坐标系M-xyz,
则平面BB1C1C的一个法向量是m=(0,0,1),A(0,0,),N(0,,0),C1(-1,,0).
设=(0==(-1,,-),
代入上式得x=-t,y=t,z=(1-t),
所以P(-t,t,t).
设平面MNP的一个法向量为n==(0,,0),=(-t,t,t),
由,得.
令z1=t,得n=(t,0,t).
因为二面角P-MN-C的平面角的大小为30°,
所以=,即=,解得t=.
所以点P为线段AC1上靠近点C1的四等分点,且坐标为P.
归纳总结
利用空间向量巧解探索性问题
(1)空间向量最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.
(2)解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.所以为使问题的解决更简单、有效,应善于运用这一方法解题.
对点训练
1.[2021·全国甲卷] 已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点.
(1)证明:BF⊥DE;
(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?
解析:(1)证明:因为E,F分别是AC和CC1的中点,且AB=BC=2,
所以CF=1,BF=.
如图,连接AF,由BF⊥A1B1,AB∥A1B1,得BF⊥AB,于是AF==3,所以AC==2.由AB2+BC2=AC2,得BA⊥BC,故以B为坐标原点,以BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系B xyz,
则B(0,0,0),E(1,1,0),F(0,2,1),
=(0,2,1).
设B1D=m(0≤m≤2),则D(m,0,2),
于是=(1-m,1,-2).
所以·=0,所以BF⊥DE.
(2)易知平面BB1C1C的一个法向量为n1=(1,0,0).
设平面DFE的法向量为n2=(x,y,z),则,
又因为=(1-m,1,-2),=(-1,1,1),
所以,令x=3,得y=m+1,z=2-m,
于是,平面DFE的一个法向量为n2=(3,m+1,2-m),
所以cos 〈n1,n2〉= .
设平面BB1C1C与平面DFE所成的二面角为θ,则sin θ=,故当m=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小,为,即当B1D=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小.
2.[2022·山东枣庄高三期末]在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,△PAD是边长为2的正三角形,BC=1,CD=,PB=.
(1)求证:平面PAD⊥底面ABCD;
(2)棱PC上是否存在点M,使二面角M-BQ-C的大小为30°?若存在,确定点M的位置;若不存在,说明理由.
解析:(1)证明:因为Q为AD的中点,PA=PD=2,
故PQ⊥AD.因为BC=DQ,BC∥DQ,
所以四边形BCDQ是平行四边形,所以BQ=CD=.
在等边三角形PAD中,PQ=PD sin60°=2×=.
又PB=,BQ=,故PQ2+BQ2=PB2,故PQ⊥BQ.
又PQ⊥AD,AD=Q,AD 平面ABCD,BQ 平面ABCD,
故PQ⊥平面ABCD.又PQ 平面PAD,
故平面PAD⊥底面ABCD.
(2)以Q为原点,所在方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系Q xyz,
则Q(0,0,0),P(0,0,),B(0,,0),C(-1,,0).
假设棱PC上存在点M,使二面角M BQ C为30°.
设=m,这里0≤m≤1.
则=m=m(-1,,-)
=(-m,m,-m).
又=(0,0,),
故==(0,0,)+(-m,m,-m)=(-m,m,m).
=(0,,0),
设平面BQM的一个法向量为m=(x,y,z),
则,即.
令x=m,则m=(m,0,m).
又n=(0,0,1)为平面CBQ的一个法向量,由二面角M-BQ-C为30°,
得cos 30°==,即=.
两边平方并化简得8m2-18m+9=0,解得m=或m=(舍).
所以=.
故棱PC上存在点M,当PM=PC时,二面角M-BQ-C为30°.
[高考5个大题] 解题研诀窍(三)
立体几何问题重在“建”——建模、建系
[思维流程——找突破口]
[技法指导——迁移搭桥]
立体几何解答题建模、建系策略
立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深,解决这类题目的原则是建模、建系.
建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型.
建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解.
[典例] 如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
[快审题]
求什么 想什么 证明线面垂直,想线面垂直成立的条件.
求线面角的正弦值,想平面的法向量及直线的方向向量.
给什么 用什么 给出边的长度,用勾股定理证线线垂直.
给出二面角的大小,可求出点M的位置.
差什么 找什么 差点M的坐标,利用垂直关系建立空间直角坐标系,找出平面PAM,平面PAC的法向量.
[稳解题]
(1)证明:因为PA=PC=AC=4,O为AC的中点,
所以PO⊥AC,且PO=2.
连接OB,因为AB=BC=AC,
所以△ABC为等腰直角三角形,
且OB⊥AC,OB=AC=2.
所以PO2+OB2=PB2,
所以PO⊥OB.
又因为OB=O,
所以PO⊥平面ABC.
(2)以O为坐标原点,
的方向为x轴正方向,
建立如图所示的空间直角坐标系O xyz.
由已知得O(0,0,0),B(2,0,0),
A(0,-2,0),C(0,2,0),P(0,0,2),
=(0,2,2).
取平面PAC的一个法向量=(2,0,0).
设M(a,2-a,0)(0设平面PAM的法向量为n=(x,y,z).
由得
令y=a,得z=-a,x=(a-4),
所以平面PAM的一个法向量为n=((a-4),a,-a),
所以cos 〈,n〉=.
由已知可得|cos 〈,n〉|=cos 30°=,
所以=,
解得a=或a=-4(舍去).
所以n=(-,-).
又因为=(0,2,-2),
所以cos 〈,n〉==.
所以PC与平面PAM所成角的正弦值为.
题后悟道
利用法向量求解空间角的关键在于“四破”
第3讲 空间向量与立体几何
考点一
考点二
考点三
考点一
向量法证明平行与垂直
考点一 向量法证明平行与垂直——建系,找点,写向量;平行,垂直,找关系
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2).
平面α,β的法向量分别为u=(a3,b3,c3),v=(a4,b4,c4).
(1)l∥m a∥b a=kb a1=______,b1=______,c1=______;
(2)l⊥m a⊥b a·b=______ a1a2+b1b2+c1c2=______;
(3)l∥α a⊥u a·u=______ a1a3+b1b3+c1c3=______;
(4)l⊥α a∥u a=ku a1=______,b1=______,c1=_____;
(5)α∥β u∥v u=kv a3=______,b3=______,c3=______;
(6)α⊥β u⊥v u·v=0 a3a4+b3b4+c3c4=______.
ka2
kb2
kc2
0
0
0
0
ka3
kb3
kc3
ka4
kb4
kc4
0
例 1 在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.
求证:(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
证明:(1)以B为坐标原点,BA,BC,BB1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系B-xyz,如图所示,
则B(0,0,0),D(0,2,2),B1(0,0,4),设BA=a,则A(a,0,0),
所以=(a,0,0),=(0,2,2),=(0,2,-2),
·=0,·=0+4-4=0,
即B1D⊥BA,B1D⊥BD.
又因为BA=B,BA,BD 平面ABD,
因此B1D⊥平面ABD.
(2)由(1)知,E(0,0,3),G,F(0,1,4),
则==(0,1,1),
·=0+2-2=0,·=0+2-2=0,
即B1D⊥EG,B1D⊥EF.
又因为EG=E,EG,EF 平面EGF,因此B1D⊥平面EGF.
结合(1)可知平面EGF∥平面ABD.
归纳总结
利用空间向量证明平行与垂直的步骤
(1)建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系;
(2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面中的要素;
(3)通过空间向量的运算研究平行、垂直关系;
(4)根据运算结果解释相关问题.
对点训练
如图,在直三棱柱ADE-BCF中,平面ABFE和平面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运用向量方法证明:
(1)OM∥平面BCF;
(2)平面MDF⊥平面EFCD.
证明:由题意得AB,AD,AE两两垂直,以A为坐标原点建立如图所示的空间直角坐标系A-xyz.
设正方形边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),
F(1,0,1),M,
O.
(1)=,
=(-1,0,0),
所以·=0,所以⊥.
因为棱柱ADE BCF是直三棱柱,所以AB⊥平面BCF,所以是平面BCF的一个法向量,且OM 平面BCF,所以OM∥平面BCF.
(2)设平面MDF与平面EFCD的一个法向量分别为n1=(x1,y1,z1),n2=(x2,y2,z2).
因为=(1,-1,1),==(1,0,0),=(0,-1,1),
由n1·=n1·=0,得
解得令x1=1,则n1=.
同理可得n2=(0,1,1).
因为n1·n2=0,所以平面MDF⊥平面EFCD.
考点二 向量法求空间角
考点二 向量法求空间角——巧妙建系,求向量夹角
向量法求异面直线所成的角
若异面直线a,b的方向向量分别为a,b,异面直线所成的角为θ,则cos θ=|cos 〈a,b〉|=.
2.向量法求线面所成的角
求出平面的法向量n,直线的方向向量a,设线面所成的角为θ,则sin θ=|cos 〈n,a〉|=.
3.向量法求二面角
求出二面角α l β的两个半平面α与β的法向量n1,n2,若二面角α l β所成的角θ为锐角,则cos θ=|cos 〈n1,n2〉|=;若二面角α l β所成的角θ为钝角,则cos θ=-|cos 〈n1,n2〉|=-.
例 2 [2022·全国乙卷理]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
解析:(1)证明:∵AD=CD,∠ADB=∠BDC,BD=BD,
∴△ABD≌△CBD,∴AB=CB.
∵E为AC的中点,∴DE⊥AC,BE⊥AC.
∵DE=E,DE,BE 平面BED,
∴AC⊥平面BED.
∵AC 平面ACD,∴平面BED⊥平面ACD.
(2)如图,连接EF.由(1)知AC⊥平面BED.
又∵EF 平面BED,
∴EF⊥AC.
∴S△AFC=AC·EF.
当EF⊥BD时,EF的长最小,此时△AFC的面积最小.
由(1)知AB=CB=2.
又∵∠ACB=60°,
∴△ABC是边长为2的正三角形,∴BE=.
∵AD⊥CD,∴DE=1,
∴DE2+BE2=BD2,∴DE⊥BE.
以点E为坐标原点,直线EA ,EB ,ED分别为x轴、y轴、z轴建立空间直角坐标系,则E(0,0,0),A(1,0,0),B(0,,0),C(-1,0,0),D(0,0,1),
∴=(-1,,0),=(-1,0,1),=(0,,-1),=(0,0,1),=(-1,0,0).
设=λ(0≤λ≤1),
则==+λ=(0,0,1)+λ(0,,-1)=(0,λ,1-λ).
∵EF⊥DB,∴·=(0,λ,1-λ)·(0,,-1)=4λ-1=0,
∴λ=,∴=(0,),∴==(0,)-(-1,0,0)=(1,).
设平面ABD的法向量为n=(x,y,z),
则即
取y=1,则x=,z=,∴n=(,1,).
设当△AFC的面积最小时,CF与平面ABD所成的角为θ,则sin θ=|cos 〈n,〉|===.
故当△AFC的面积最小时,CF与平面ABD所成的角的正弦值为.
归纳总结
1.利用向量法求线面角的方法
(1)分别求出斜线和它在平面内的射影的方向向量,转化为求两个方向向量的夹角(或其补角);
(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(或钝角的补角),取其余角就是斜线和平面所成的角.即线面角的正弦值等于斜线的方向向量与平面的法向量夹角余弦值的绝对值.
2.利用向量法求二面角的方法
(1)分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的大小;
(2)通过平面的法向量来求:设二面角的两个半平面的法向量分别为n1和n2,则二面角的大小等于〈n1,n2〉(或π-〈n1,n2〉).
提醒
求空间角注意:①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|.②两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角.③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值,即注意函数名称的变化.
对点训练
[2021·全国乙卷改编]如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.
(1)求BC;
(2)求二面角A-PM B的正弦值;
(3)求直线PB与CD所成的角;
(4)求直线PB与平面PAM所成角的正弦值.
解析:(1)因为PD⊥平面ABCD,所以PD⊥AD,PD⊥DC.
在矩形ABCD中,AD⊥DC,故以点D为坐标原点建立空间直角坐标系如图所示,
设BC=t,则A(t,0,0),B(t,1,0),M,P(0,0,1),
所以=(t,1,-1),=.
因为PB⊥AM,所以·=-+1=0,得t=,
所以BC=.
(2)易知C(0,1,0),由(1)可得=(-,0,1),==(,0,0),=(,1,-1).
设平面APM的法向量为n1=(x1,y1,z1),则
,即,
令x1=,则z1=2,y1=1,所以平面APM的一个法向量n1=(,1,2).
设平面PMB的法向量为n2=(x2,y2,z2),则
,即,
得x2=0,令y2=1,则z2=1,所以平面PMB的一个法向量为n2=(0,1,1).
cos 〈n1,n2〉===,
所以二面角A PM B的正弦值为.
(3)由题意知:
P(0,0,1),B(,1,0),C(0,1,0),D(0,0,0),则=(0,1,0),=(,1,-1),设直线PB与CD所成角的大小为θ,
则cos θ=|cos 〈〉|===.
又因为θ∈,
所以θ=,
即直线PB与CD所成的角为.
(4)由题意知:P(0,0,1),B(,1,0),A(,0,0),M.
则=(,1,-1),=.=.
设n=(x,y,z)为平面PAM的法向量,
则即
令x=2,则y=,z=2.所以n=(2,,2).
设直线PB与平面PAM所成角的大小为θ,则
sin θ=|cos 〈,n〉|===,
即直线PB与平面PAM所成角的正弦值为.
考点三
用向量法解决探索性问题
考点三 用向量法解决探索性问题——问题坐标化,探求方程解
与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
例 3 [2022·河北深州市高三期末]如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,BC⊥BB1,CC1=,AC1=.
(1)证明:平面ABC⊥平面BB1C1C;
(2)M,N分别是BC,B1C1的中点,P是线段AC1上的动点,若二面角P MN C的平面角的大小为30°,试确定点P的位置.
解析:(1)证明:因为AC=2,CC1=,AC1=,
所以=,即AC⊥CC1.
又因为BC⊥BB1,BB1∥CC1,所以BC⊥CC1,
AC=C,所以CC1⊥平面ABC.
因为CC1 平面BB1C1C,所以平面ABC⊥平面BB1C1C.
(2)连接AM,因为AB=AC=2,M是BC的中点,所以AM⊥BC.
由(1)知,平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC,所以AM⊥平面BB1C1C.
以M为原点建立如图所示的空间直角坐标系M-xyz,
则平面BB1C1C的一个法向量是m=(0,0,1),A(0,0,),N(0,,0),C1(-1,,0).
设=(0
代入上式得x=-t,y=t,z=(1-t),
所以P(-t,t,t).
设平面MNP的一个法向量为n==(0,,0),=(-t,t,t),
由,得.
令z1=t,得n=(t,0,t).
因为二面角P-MN-C的平面角的大小为30°,
所以=,即=,解得t=.
所以点P为线段AC1上靠近点C1的四等分点,且坐标为P.
归纳总结
利用空间向量巧解探索性问题
(1)空间向量最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.
(2)解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.所以为使问题的解决更简单、有效,应善于运用这一方法解题.
对点训练
1.[2021·全国甲卷] 已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点.
(1)证明:BF⊥DE;
(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?
解析:(1)证明:因为E,F分别是AC和CC1的中点,且AB=BC=2,
所以CF=1,BF=.
如图,连接AF,由BF⊥A1B1,AB∥A1B1,得BF⊥AB,于是AF==3,所以AC==2.由AB2+BC2=AC2,得BA⊥BC,故以B为坐标原点,以BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系B xyz,
则B(0,0,0),E(1,1,0),F(0,2,1),
=(0,2,1).
设B1D=m(0≤m≤2),则D(m,0,2),
于是=(1-m,1,-2).
所以·=0,所以BF⊥DE.
(2)易知平面BB1C1C的一个法向量为n1=(1,0,0).
设平面DFE的法向量为n2=(x,y,z),则,
又因为=(1-m,1,-2),=(-1,1,1),
所以,令x=3,得y=m+1,z=2-m,
于是,平面DFE的一个法向量为n2=(3,m+1,2-m),
所以cos 〈n1,n2〉= .
设平面BB1C1C与平面DFE所成的二面角为θ,则sin θ=,故当m=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小,为,即当B1D=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小.
2.[2022·山东枣庄高三期末]在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,△PAD是边长为2的正三角形,BC=1,CD=,PB=.
(1)求证:平面PAD⊥底面ABCD;
(2)棱PC上是否存在点M,使二面角M-BQ-C的大小为30°?若存在,确定点M的位置;若不存在,说明理由.
解析:(1)证明:因为Q为AD的中点,PA=PD=2,
故PQ⊥AD.因为BC=DQ,BC∥DQ,
所以四边形BCDQ是平行四边形,所以BQ=CD=.
在等边三角形PAD中,PQ=PD sin60°=2×=.
又PB=,BQ=,故PQ2+BQ2=PB2,故PQ⊥BQ.
又PQ⊥AD,AD=Q,AD 平面ABCD,BQ 平面ABCD,
故PQ⊥平面ABCD.又PQ 平面PAD,
故平面PAD⊥底面ABCD.
(2)以Q为原点,所在方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系Q xyz,
则Q(0,0,0),P(0,0,),B(0,,0),C(-1,,0).
假设棱PC上存在点M,使二面角M BQ C为30°.
设=m,这里0≤m≤1.
则=m=m(-1,,-)
=(-m,m,-m).
又=(0,0,),
故==(0,0,)+(-m,m,-m)=(-m,m,m).
=(0,,0),
设平面BQM的一个法向量为m=(x,y,z),
则,即.
令x=m,则m=(m,0,m).
又n=(0,0,1)为平面CBQ的一个法向量,由二面角M-BQ-C为30°,
得cos 30°==,即=.
两边平方并化简得8m2-18m+9=0,解得m=或m=(舍).
所以=.
故棱PC上存在点M,当PM=PC时,二面角M-BQ-C为30°.
[高考5个大题] 解题研诀窍(三)
立体几何问题重在“建”——建模、建系
[思维流程——找突破口]
[技法指导——迁移搭桥]
立体几何解答题建模、建系策略
立体几何解答题的基本模式是论证推理与计算相结合,以某个几何体为依托,分步设问,逐层加深,解决这类题目的原则是建模、建系.
建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型.
建系——依托于题中的垂直条件,建立空间直角坐标系,利用空间向量求解.
[典例] 如图,在三棱锥P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.
[快审题]
求什么 想什么 证明线面垂直,想线面垂直成立的条件.
求线面角的正弦值,想平面的法向量及直线的方向向量.
给什么 用什么 给出边的长度,用勾股定理证线线垂直.
给出二面角的大小,可求出点M的位置.
差什么 找什么 差点M的坐标,利用垂直关系建立空间直角坐标系,找出平面PAM,平面PAC的法向量.
[稳解题]
(1)证明:因为PA=PC=AC=4,O为AC的中点,
所以PO⊥AC,且PO=2.
连接OB,因为AB=BC=AC,
所以△ABC为等腰直角三角形,
且OB⊥AC,OB=AC=2.
所以PO2+OB2=PB2,
所以PO⊥OB.
又因为OB=O,
所以PO⊥平面ABC.
(2)以O为坐标原点,
的方向为x轴正方向,
建立如图所示的空间直角坐标系O xyz.
由已知得O(0,0,0),B(2,0,0),
A(0,-2,0),C(0,2,0),P(0,0,2),
=(0,2,2).
取平面PAC的一个法向量=(2,0,0).
设M(a,2-a,0)(0
由得
令y=a,得z=-a,x=(a-4),
所以平面PAM的一个法向量为n=((a-4),a,-a),
所以cos 〈,n〉=.
由已知可得|cos 〈,n〉|=cos 30°=,
所以=,
解得a=或a=-4(舍去).
所以n=(-,-).
又因为=(0,2,-2),
所以cos 〈,n〉==.
所以PC与平面PAM所成角的正弦值为.
题后悟道
利用法向量求解空间角的关键在于“四破”
同课章节目录
