(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题五 解析几何 第2讲 圆锥曲线的定义、方程与性质 课件(39张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题五 解析几何 第2讲 圆锥曲线的定义、方程与性质 课件(39张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 06:01:41 | ||
图片预览







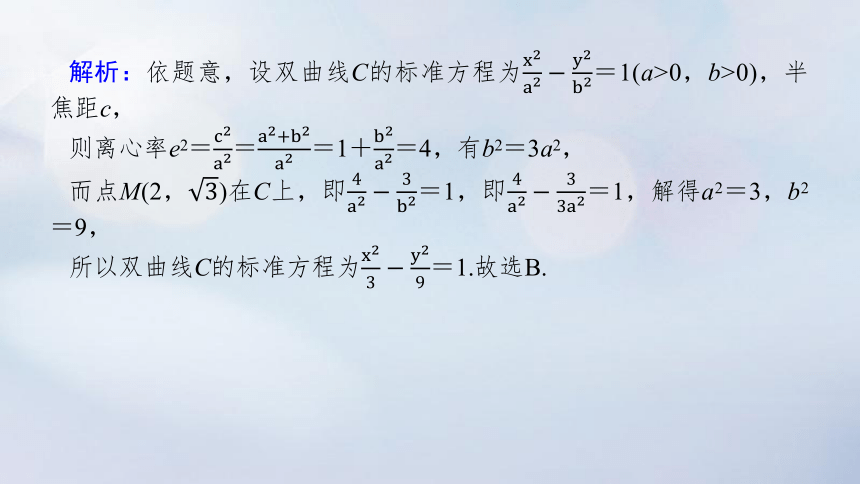




文档简介
(共39张PPT)
第2讲 圆锥曲线的定义、方程与性质
考点一
考点二
考点三
考点一 圆锥曲线的定义及标准方程——回归定义,巧解方程
考点一 圆锥曲线的定义及标准方程——回归定义,巧解方程
圆锥曲线的定义、标准方程
名称 椭圆 双曲线 抛物线
定义 |PF1|+|PF2|=2a(2a>|F1F2|) ||PF1|-|PF2||=2a(0<2a<|F1F2|) |PF|=|PM|,点F不在直线l上,PM⊥l于M
标准 方程 y2=2px
(p>0)
图形
例 1 (1)[2022·全国甲卷]已知椭圆C:=1(a>b>0)的离心率为,A1,A2分别为C的左、右顶点,B为C的上顶点.若=-1,则C的方程为( )
A.=1 B.=1
C.=1 D.+y2=1
答案:B
解析:由椭圆C的离心率为,可得e===.化简,得8a2=9b2.易知A1(-a,0),A2(a,0),B(0,b),所以=(-a,-b)·(a,-b)=-a2+b2=-1.联立得方程组解得所以C的方程为=1.故选B.
(2)[2022·贵州毕节模拟预测]如图,唐金筐宝钿团花纹金杯出土于西安,这件金杯整体造型具有玲珑剔透之美,充分体现唐代金银器制作的高超技艺,是唐代金银细工的典范之作.该杯主体部分的轴截面可以近似看作双曲线C的一部分,若C的中心在原点,焦点在x轴上,离心率e=2,且点M(2,)在C上,则双曲线C的标准方程为( )
A.x2-=1 B.=1
C.-y2=1 D.=1
答案:B
解析:依题意,设双曲线C的标准方程为=1(a>0,b>0),半焦距c,
则离心率e2===1+=4,有b2=3a2,
而点M(2,)在C上,即=1,即=1,解得a2=3,b2=9,
所以双曲线C的标准方程为=1.故选B.
归纳总结
1.关于圆锥曲线定义的应用
对于椭圆、双曲线如果涉及曲线上的点与焦点的距离,一般要利用定义进行转化.对应抛物线涉及曲线上点到焦点的距离、到准线的距离时需要相互转化.
2.关于圆锥曲线方程的求法
定型 确定曲线类型
计算 利用待定系数法,根据条件求出系数a,b,c,p
对点训练
1.[2022·湖南周南中学期末]已知椭圆C:=1的左右焦点分别为F1、F2,过左焦点F1作直线交椭圆C于A、B两点,则三角形ABF2的周长为( )
A.10 B.15 C.20 D.25
答案:C
解析:由题意,椭圆的长轴为2a=2=10,由椭圆定义知AF1+F1B=2a,AF2+BF2=2a,
=AB+AF2+BF2=AF1+F1B+AF2+BF2=4a=20,故选C.
2.已知P是抛物线y2=4x上的一个动点,Q是圆(x-3)2+(y-1)2=1上的一个动点,N(1,0)是一个定点,则|PQ|+|PN|的最小值为( )
A.3 B.4 C.5 D.+1
答案:A
解析: 如图所示,由抛物线方程y2=4x,可得抛物线的焦点F(1,0),又N(1,0),所以N与F重合.过圆(x-3)2+(y-1)2=1的圆心M作抛物线准线的垂线MH,交圆于Q,交抛物线于P,则|PQ|+|PN|的最小值等于|MH|-1=3.
考点二 圆锥曲线的几何性质——找准a、b、c,数形要结合
考点二 圆锥曲线的几何性质——找准a、b、c,数形要结合
圆锥曲线的重要性质
(1)椭圆、双曲线中,a,b,c之间的关系
①在椭圆中:a2=b2+c2,离心率为e=________=__________;
②在双曲线中:c2=a2+b2,离心率为e=______=__________.
(2)双曲线的渐近线方程与焦点坐标:
①双曲线=1(a>0,b>0)的渐近线方程为y=________,焦点坐标F1(-c,0),F2(c,0);
②双曲线=1(a>0,b>0)的渐近线方程为y=________,焦点坐标F1(0,-c),F2(0,c).
±x
±x
(3)抛物线的焦点坐标与准线方程:
①抛物线y2=±2px(p>0)的焦点坐标为___________,准线方程为x=________;
②抛物线x2=±2py(p>0)的焦点坐标为___________,准线方程为y=________.
例 2 (1)[2022·全国甲卷]椭圆C:=1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为,则C的离心率为( )
A. B. C. D.
答案:A
解析:设P(x1,y1),则点Q的坐标为(-x1,y1).由题意,得点A(-a,0).又直线AP,AQ的斜率之积为,所以·=,即= ①.又点P在椭圆C上,所以=1 ②.由①②,得=,所以a2=4b2,所以a2=4(a2-c2),所以椭圆C的离心率e==.故选A.
(2)[2022·全国乙卷]设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=( )
A.2 B.2 C.3 D.3
答案:B
解析:由已知条件,易知抛物线y2=4x的焦点为F(1,0),准线方程为x=-1.又B(3,0),则|AF|=|BF|=2.不妨设点A在第一象限,则A(x0,2).根据抛物线的定义可知x0-(-1)=2,所以x0=1,所以A(1,2),所以|AB|==2.故选B.
(3)[2022·全国乙卷]双曲线C的两个焦点为F1,F2,以C的实轴为直径的圆记为D,过F1作D的切线与C交于M,N两点,且=,则C的离心率为( )
A. B. C. D.
答案:AC
解析:不妨假设双曲线的标准方程为=1(a>0,b>0),F1(-c,0),F2(c,0).当两个交点M,N在双曲线两支上时,如图1所示,设过F1的直线与圆D切于点P,连接OP,由题意知|OP|=a,又|OF1|=c,所以|F1P|=b.过点F2作F2Q⊥F1N,交F1N于点Q.由中位线的性质,可得|F2Q|=2|OP|=2a,|PQ|=b.因为cos ∠F1NF2=,所以sin ∠F1NF2=,
故|NF2|=a,|QN|=a,所以|NF1|=|F1Q|+|QN|=
2b+a.由双曲线的定义可知|NF1|-|NF2|=2a,所以
2b+a-a=2a,所以2b=3a.两边平方得4b2=9a2,
即4(c2-a2)=9a2,整理得4c2=13a2,所以=,
故=,即e=.
当两个交点M,N都在双曲线的左支上时,如图2所示,同理可得|F2Q|=2|OP|=2a,|PQ|=b.因为cos ∠F1NF2=,所以sin ∠F1NF2=,可得|NF2|=,|NQ|=,所以|NF1|=|NQ|-|QF1|=-2b,所以|NF2|=|NF1|+2a=-2b,又|NF2|=,所以-2b=,即a=2b,e==.故选AC.
归纳总结
1.椭圆、双曲线的离心率(或范围)的求法
求椭圆、双曲线的离心率或离心率的范围,关键是根据已知条件确定a,b,c的等量关系或不等关系,然后把b用a,c代换,求的值.
2.双曲线的渐近线的求法及用法
(1)求法:把双曲线标准方程等号右边的“1”改为零,分解因式可得;
(2)用法:①可得或的值;
②利用渐近线方程设所求双曲线的方程.
对点训练
1.[2021·全国甲卷]已知F1,F2是双曲线C的两个焦点,P为C上一点,且∠F1PF2=60°,|PF1|=3|PF2|,则C的离心率为( )
A. B. C. D.
答案:A
解析:设|PF2|=m,|PF1|=3m,则|F1F2|==m,所以C的离心率e=====,故选A.
2.[2021·全国乙卷]设B是椭圆C:+y2=1的上顶点,点P在C上,则|PB|的最大值为( )
A. B. C. D.2
答案:A
解析:通解 设点P(x,y),则根据点P在椭圆+y2=1上可得x2=5-5y2.易知点B(0,1),所以根据两点间的距离公式得|PB|2=x2+(y-1)2=5-5y2+(y-1)2=-2y+6=-(2y+)2.
当2y+=0,即y=-(满足|y|≤1)时,|PB|2取得最大值,所以|PB|max=.故选A.
优解 因为点P在椭圆+y2=1上,所以可设点P(cos θ,sin θ).易知点B(0,1),所以根据两点间的距离公式得|PB|2=(cos θ)2+(sin θ-1)2=4cos2θ-2sinθ+2=-4sin2θ-2sinθ+6=-(2sin θ+)2.易知当2sin θ+=0,即sin θ=-时,|PB|2取得最大值,所以=.故选A.
3.[2021·全国乙卷]设B是椭圆C:=1(a>b>0)的上顶点,若C上的任意一点P都满足|PB|≤2b,则C的离心率的取值范围是( )
A.[,1) B.
C.(0,] D.
答案:C
解析:解法一 依题意,B(0,b),设P(a cos θ,b sin θ),θ∈[0,2π),因为|PB|≤2b,所以对任意θ∈[0,2π),(a cos θ)2+(b sin θ-b)2≤4b2恒成立,即(a2-b2)sin2θ+2b2sinθ+3b2-a2≥0对任意θ∈[0,2π)恒成立.令sin θ=t,t∈[-1,1],f(t)=(a2-b2)t2+2b2t+3b2-a2,则原问题转化为对任意t∈[-1,1],恒有f(t)≥0成立.因为f(-1)=0,所以只需-≤-1即可,所以2b2≥a2,则离心率e= ≤ ,所以选C.
解法二 依题意,B(0,b),设椭圆上一点P(x0,y0),则=1,可得=,则|PB|2=+(y0-b)2=-2by0+b2=-2by0+a2+b2≤4b2.因为当y0=-b时,|PB|2=4b2,所以-≤-b,得2c2≤a2,所以离心率e=≤ ,故选C.
考点三 直线与圆锥曲线的关系及应用
——联立方程,设而不求
考点三 直线与圆锥曲线的关系及应用——联立方程,设而不求
1.弦长公式
设直线斜率为k,直线与圆锥曲线交于A(x1,y1),B(x2,y2)时,|AB|
=_____________=______________________或|AB|=______________
=________________________.
2.过抛物线焦点的弦长
过抛物线y2=2px(p>0)焦点F的弦AB,若A(x1,y1),B(x2,y2),则x1x2
=________,y1y2=________,弦长|AB|=________.
|x1-x2|
|y1-y2|
-p2
x1+x2+p
例 3 (1)[2022·浙江卷]已知双曲线=1(a>0,b>0)的左焦点为F,过F且斜率为的直线交双曲线于点A(x1,y1),交双曲线的渐近线于点B(x2,y2),且x1<0答案:
解析:由题意,得F(-c,0),点B在双曲线的渐近线y=x上,所以B(x2,x2).由直线FB的斜率为,得=,解得x2=,所以B().因为|FB|=3|FA|,所以=3,所以(+c,)=3(x1+c,y1),解得x1=-,y1=,即A(-).将点A的坐标代入双曲线的方程,得=1,即=1,解得e=(负值已舍去).
(2)[2022·新高考Ⅱ卷]已知直线l与椭圆=1在第一象限交于A,B两点,l与x轴、y轴分别交于M,N两点,且|MA|=|NB|,|MN|=2,则l的方程为______________.
x+y-2=0
解析:方法一 取线段AB的中点E,连接OE(O为坐标原点).因为|MA|=|NB|,所以|ME|=|NE|.设A(x1,y1),B(x2,y2).由题意可得===-,即kOE·kAB=-.设直线AB的方程为y=kx+m,k<0,m>0.令x=0,则y=m.令y=0,则x=-.所以点E的坐标为(-),所以k×=-k2=-,解得k=-,所以m2+2m2=12,解得m=2,所以直线AB的方程为y=-x+2,即x+y-2=0.
方法二 设线段AB的中点为E.由|MA|=|NB|,得E为线段MN的中点.设直线AB的方程为y=kx+m,k<0,m>0,则M(-,0),N(0,m),E(-).将y=kx+m代入=1中并整理,得(1+2k2)x2+4kmx+2m2-6=0.由Δ=6k2-m2+3>0,得m2<6k2+3.设A(x1,y1),B(x2,y2),则x1+x2==2·(-),解得k=-.又因为|MN|= =2,所以m=2,符合题意,所以直线AB的方程为x+y-2=0.
归纳总结
直线与圆锥曲线关系的求解技巧
(1)对于弦中点问题常用“根与系数的关系”或“点差法”求解,在使用根与系数的关系时,要注意使用条件Δ>0,在用“点差法”时,要检验直线与圆锥曲线是否相交.
(2)椭圆=1(a>b>0)截直线所得的弦的中点是P(x0,y0)(y0≠0),则直线的斜率为-.
(3)双曲线=1(a>0,b>0)上以P(x0,y0)(y0≠0)为中点的弦所在直线的斜率为k=.
对点训练
1.[2022·河南洛阳]已知点F是双曲线x2-=1的右焦点,点P是双曲线上在第一象限内的一点,且PF与x轴垂直,点Q是双曲线渐近线上的动点,则的最小值为( )
A.2 B.2
C.1- D.1+
答案:B
解析:由双曲线方程可得,点F坐标为(3,0),将x=3代入双曲线方程,得y=±8,
由于点P在第一象限,所以点P坐标为(3,8),
双曲线的渐近线方程为2x±y=0,点P到双曲线的渐近线的距离为.
Q是双曲线渐近线上的动点,所以的最小值为=2.故选B.
2.[2022·贵州贵阳一中]过抛物线C:y2=2px(p>0)的焦点F的直线l与抛物线C交于点A,B,若=2,若直线l的斜率为k,则k=( )
A.2 B.-2
C.2或-2 D.或-
答案:C
解析:当A在x轴上方时,过A,B分别作抛物线准线的垂线,垂足分别为A1,B1,过B作BD⊥AA1于D,
设=r,则=3r,=r,所以==2r,
所以k=tan ∠BAD===2,同理可得当A在x轴下方时,k的值为-2,故选C.
第2讲 圆锥曲线的定义、方程与性质
考点一
考点二
考点三
考点一 圆锥曲线的定义及标准方程——回归定义,巧解方程
考点一 圆锥曲线的定义及标准方程——回归定义,巧解方程
圆锥曲线的定义、标准方程
名称 椭圆 双曲线 抛物线
定义 |PF1|+|PF2|=2a(2a>|F1F2|) ||PF1|-|PF2||=2a(0<2a<|F1F2|) |PF|=|PM|,点F不在直线l上,PM⊥l于M
标准 方程 y2=2px
(p>0)
图形
例 1 (1)[2022·全国甲卷]已知椭圆C:=1(a>b>0)的离心率为,A1,A2分别为C的左、右顶点,B为C的上顶点.若=-1,则C的方程为( )
A.=1 B.=1
C.=1 D.+y2=1
答案:B
解析:由椭圆C的离心率为,可得e===.化简,得8a2=9b2.易知A1(-a,0),A2(a,0),B(0,b),所以=(-a,-b)·(a,-b)=-a2+b2=-1.联立得方程组解得所以C的方程为=1.故选B.
(2)[2022·贵州毕节模拟预测]如图,唐金筐宝钿团花纹金杯出土于西安,这件金杯整体造型具有玲珑剔透之美,充分体现唐代金银器制作的高超技艺,是唐代金银细工的典范之作.该杯主体部分的轴截面可以近似看作双曲线C的一部分,若C的中心在原点,焦点在x轴上,离心率e=2,且点M(2,)在C上,则双曲线C的标准方程为( )
A.x2-=1 B.=1
C.-y2=1 D.=1
答案:B
解析:依题意,设双曲线C的标准方程为=1(a>0,b>0),半焦距c,
则离心率e2===1+=4,有b2=3a2,
而点M(2,)在C上,即=1,即=1,解得a2=3,b2=9,
所以双曲线C的标准方程为=1.故选B.
归纳总结
1.关于圆锥曲线定义的应用
对于椭圆、双曲线如果涉及曲线上的点与焦点的距离,一般要利用定义进行转化.对应抛物线涉及曲线上点到焦点的距离、到准线的距离时需要相互转化.
2.关于圆锥曲线方程的求法
定型 确定曲线类型
计算 利用待定系数法,根据条件求出系数a,b,c,p
对点训练
1.[2022·湖南周南中学期末]已知椭圆C:=1的左右焦点分别为F1、F2,过左焦点F1作直线交椭圆C于A、B两点,则三角形ABF2的周长为( )
A.10 B.15 C.20 D.25
答案:C
解析:由题意,椭圆的长轴为2a=2=10,由椭圆定义知AF1+F1B=2a,AF2+BF2=2a,
=AB+AF2+BF2=AF1+F1B+AF2+BF2=4a=20,故选C.
2.已知P是抛物线y2=4x上的一个动点,Q是圆(x-3)2+(y-1)2=1上的一个动点,N(1,0)是一个定点,则|PQ|+|PN|的最小值为( )
A.3 B.4 C.5 D.+1
答案:A
解析: 如图所示,由抛物线方程y2=4x,可得抛物线的焦点F(1,0),又N(1,0),所以N与F重合.过圆(x-3)2+(y-1)2=1的圆心M作抛物线准线的垂线MH,交圆于Q,交抛物线于P,则|PQ|+|PN|的最小值等于|MH|-1=3.
考点二 圆锥曲线的几何性质——找准a、b、c,数形要结合
考点二 圆锥曲线的几何性质——找准a、b、c,数形要结合
圆锥曲线的重要性质
(1)椭圆、双曲线中,a,b,c之间的关系
①在椭圆中:a2=b2+c2,离心率为e=________=__________;
②在双曲线中:c2=a2+b2,离心率为e=______=__________.
(2)双曲线的渐近线方程与焦点坐标:
①双曲线=1(a>0,b>0)的渐近线方程为y=________,焦点坐标F1(-c,0),F2(c,0);
②双曲线=1(a>0,b>0)的渐近线方程为y=________,焦点坐标F1(0,-c),F2(0,c).
±x
±x
(3)抛物线的焦点坐标与准线方程:
①抛物线y2=±2px(p>0)的焦点坐标为___________,准线方程为x=________;
②抛物线x2=±2py(p>0)的焦点坐标为___________,准线方程为y=________.
例 2 (1)[2022·全国甲卷]椭圆C:=1(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称.若直线AP,AQ的斜率之积为,则C的离心率为( )
A. B. C. D.
答案:A
解析:设P(x1,y1),则点Q的坐标为(-x1,y1).由题意,得点A(-a,0).又直线AP,AQ的斜率之积为,所以·=,即= ①.又点P在椭圆C上,所以=1 ②.由①②,得=,所以a2=4b2,所以a2=4(a2-c2),所以椭圆C的离心率e==.故选A.
(2)[2022·全国乙卷]设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=( )
A.2 B.2 C.3 D.3
答案:B
解析:由已知条件,易知抛物线y2=4x的焦点为F(1,0),准线方程为x=-1.又B(3,0),则|AF|=|BF|=2.不妨设点A在第一象限,则A(x0,2).根据抛物线的定义可知x0-(-1)=2,所以x0=1,所以A(1,2),所以|AB|==2.故选B.
(3)[2022·全国乙卷]双曲线C的两个焦点为F1,F2,以C的实轴为直径的圆记为D,过F1作D的切线与C交于M,N两点,且=,则C的离心率为( )
A. B. C. D.
答案:AC
解析:不妨假设双曲线的标准方程为=1(a>0,b>0),F1(-c,0),F2(c,0).当两个交点M,N在双曲线两支上时,如图1所示,设过F1的直线与圆D切于点P,连接OP,由题意知|OP|=a,又|OF1|=c,所以|F1P|=b.过点F2作F2Q⊥F1N,交F1N于点Q.由中位线的性质,可得|F2Q|=2|OP|=2a,|PQ|=b.因为cos ∠F1NF2=,所以sin ∠F1NF2=,
故|NF2|=a,|QN|=a,所以|NF1|=|F1Q|+|QN|=
2b+a.由双曲线的定义可知|NF1|-|NF2|=2a,所以
2b+a-a=2a,所以2b=3a.两边平方得4b2=9a2,
即4(c2-a2)=9a2,整理得4c2=13a2,所以=,
故=,即e=.
当两个交点M,N都在双曲线的左支上时,如图2所示,同理可得|F2Q|=2|OP|=2a,|PQ|=b.因为cos ∠F1NF2=,所以sin ∠F1NF2=,可得|NF2|=,|NQ|=,所以|NF1|=|NQ|-|QF1|=-2b,所以|NF2|=|NF1|+2a=-2b,又|NF2|=,所以-2b=,即a=2b,e==.故选AC.
归纳总结
1.椭圆、双曲线的离心率(或范围)的求法
求椭圆、双曲线的离心率或离心率的范围,关键是根据已知条件确定a,b,c的等量关系或不等关系,然后把b用a,c代换,求的值.
2.双曲线的渐近线的求法及用法
(1)求法:把双曲线标准方程等号右边的“1”改为零,分解因式可得;
(2)用法:①可得或的值;
②利用渐近线方程设所求双曲线的方程.
对点训练
1.[2021·全国甲卷]已知F1,F2是双曲线C的两个焦点,P为C上一点,且∠F1PF2=60°,|PF1|=3|PF2|,则C的离心率为( )
A. B. C. D.
答案:A
解析:设|PF2|=m,|PF1|=3m,则|F1F2|==m,所以C的离心率e=====,故选A.
2.[2021·全国乙卷]设B是椭圆C:+y2=1的上顶点,点P在C上,则|PB|的最大值为( )
A. B. C. D.2
答案:A
解析:通解 设点P(x,y),则根据点P在椭圆+y2=1上可得x2=5-5y2.易知点B(0,1),所以根据两点间的距离公式得|PB|2=x2+(y-1)2=5-5y2+(y-1)2=-2y+6=-(2y+)2.
当2y+=0,即y=-(满足|y|≤1)时,|PB|2取得最大值,所以|PB|max=.故选A.
优解 因为点P在椭圆+y2=1上,所以可设点P(cos θ,sin θ).易知点B(0,1),所以根据两点间的距离公式得|PB|2=(cos θ)2+(sin θ-1)2=4cos2θ-2sinθ+2=-4sin2θ-2sinθ+6=-(2sin θ+)2.易知当2sin θ+=0,即sin θ=-时,|PB|2取得最大值,所以=.故选A.
3.[2021·全国乙卷]设B是椭圆C:=1(a>b>0)的上顶点,若C上的任意一点P都满足|PB|≤2b,则C的离心率的取值范围是( )
A.[,1) B.
C.(0,] D.
答案:C
解析:解法一 依题意,B(0,b),设P(a cos θ,b sin θ),θ∈[0,2π),因为|PB|≤2b,所以对任意θ∈[0,2π),(a cos θ)2+(b sin θ-b)2≤4b2恒成立,即(a2-b2)sin2θ+2b2sinθ+3b2-a2≥0对任意θ∈[0,2π)恒成立.令sin θ=t,t∈[-1,1],f(t)=(a2-b2)t2+2b2t+3b2-a2,则原问题转化为对任意t∈[-1,1],恒有f(t)≥0成立.因为f(-1)=0,所以只需-≤-1即可,所以2b2≥a2,则离心率e= ≤ ,所以选C.
解法二 依题意,B(0,b),设椭圆上一点P(x0,y0),则=1,可得=,则|PB|2=+(y0-b)2=-2by0+b2=-2by0+a2+b2≤4b2.因为当y0=-b时,|PB|2=4b2,所以-≤-b,得2c2≤a2,所以离心率e=≤ ,故选C.
考点三 直线与圆锥曲线的关系及应用
——联立方程,设而不求
考点三 直线与圆锥曲线的关系及应用——联立方程,设而不求
1.弦长公式
设直线斜率为k,直线与圆锥曲线交于A(x1,y1),B(x2,y2)时,|AB|
=_____________=______________________或|AB|=______________
=________________________.
2.过抛物线焦点的弦长
过抛物线y2=2px(p>0)焦点F的弦AB,若A(x1,y1),B(x2,y2),则x1x2
=________,y1y2=________,弦长|AB|=________.
|x1-x2|
|y1-y2|
-p2
x1+x2+p
例 3 (1)[2022·浙江卷]已知双曲线=1(a>0,b>0)的左焦点为F,过F且斜率为的直线交双曲线于点A(x1,y1),交双曲线的渐近线于点B(x2,y2),且x1<0
解析:由题意,得F(-c,0),点B在双曲线的渐近线y=x上,所以B(x2,x2).由直线FB的斜率为,得=,解得x2=,所以B().因为|FB|=3|FA|,所以=3,所以(+c,)=3(x1+c,y1),解得x1=-,y1=,即A(-).将点A的坐标代入双曲线的方程,得=1,即=1,解得e=(负值已舍去).
(2)[2022·新高考Ⅱ卷]已知直线l与椭圆=1在第一象限交于A,B两点,l与x轴、y轴分别交于M,N两点,且|MA|=|NB|,|MN|=2,则l的方程为______________.
x+y-2=0
解析:方法一 取线段AB的中点E,连接OE(O为坐标原点).因为|MA|=|NB|,所以|ME|=|NE|.设A(x1,y1),B(x2,y2).由题意可得===-,即kOE·kAB=-.设直线AB的方程为y=kx+m,k<0,m>0.令x=0,则y=m.令y=0,则x=-.所以点E的坐标为(-),所以k×=-k2=-,解得k=-,所以m2+2m2=12,解得m=2,所以直线AB的方程为y=-x+2,即x+y-2=0.
方法二 设线段AB的中点为E.由|MA|=|NB|,得E为线段MN的中点.设直线AB的方程为y=kx+m,k<0,m>0,则M(-,0),N(0,m),E(-).将y=kx+m代入=1中并整理,得(1+2k2)x2+4kmx+2m2-6=0.由Δ=6k2-m2+3>0,得m2<6k2+3.设A(x1,y1),B(x2,y2),则x1+x2==2·(-),解得k=-.又因为|MN|= =2,所以m=2,符合题意,所以直线AB的方程为x+y-2=0.
归纳总结
直线与圆锥曲线关系的求解技巧
(1)对于弦中点问题常用“根与系数的关系”或“点差法”求解,在使用根与系数的关系时,要注意使用条件Δ>0,在用“点差法”时,要检验直线与圆锥曲线是否相交.
(2)椭圆=1(a>b>0)截直线所得的弦的中点是P(x0,y0)(y0≠0),则直线的斜率为-.
(3)双曲线=1(a>0,b>0)上以P(x0,y0)(y0≠0)为中点的弦所在直线的斜率为k=.
对点训练
1.[2022·河南洛阳]已知点F是双曲线x2-=1的右焦点,点P是双曲线上在第一象限内的一点,且PF与x轴垂直,点Q是双曲线渐近线上的动点,则的最小值为( )
A.2 B.2
C.1- D.1+
答案:B
解析:由双曲线方程可得,点F坐标为(3,0),将x=3代入双曲线方程,得y=±8,
由于点P在第一象限,所以点P坐标为(3,8),
双曲线的渐近线方程为2x±y=0,点P到双曲线的渐近线的距离为.
Q是双曲线渐近线上的动点,所以的最小值为=2.故选B.
2.[2022·贵州贵阳一中]过抛物线C:y2=2px(p>0)的焦点F的直线l与抛物线C交于点A,B,若=2,若直线l的斜率为k,则k=( )
A.2 B.-2
C.2或-2 D.或-
答案:C
解析:当A在x轴上方时,过A,B分别作抛物线准线的垂线,垂足分别为A1,B1,过B作BD⊥AA1于D,
设=r,则=3r,=r,所以==2r,
所以k=tan ∠BAD===2,同理可得当A在x轴下方时,k的值为-2,故选C.
同课章节目录
