(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题五 解析几何 第3讲 圆锥曲线的综合问题 课件(54张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题五 解析几何 第3讲 圆锥曲线的综合问题 课件(54张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 06:02:24 | ||
图片预览






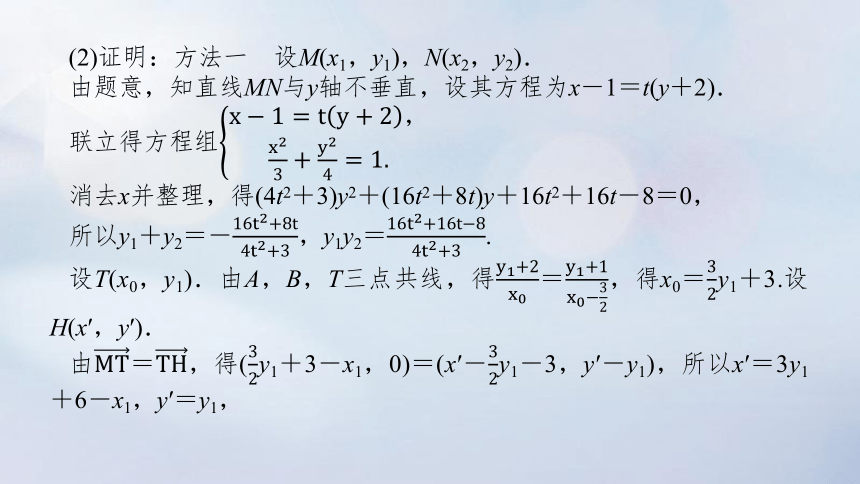
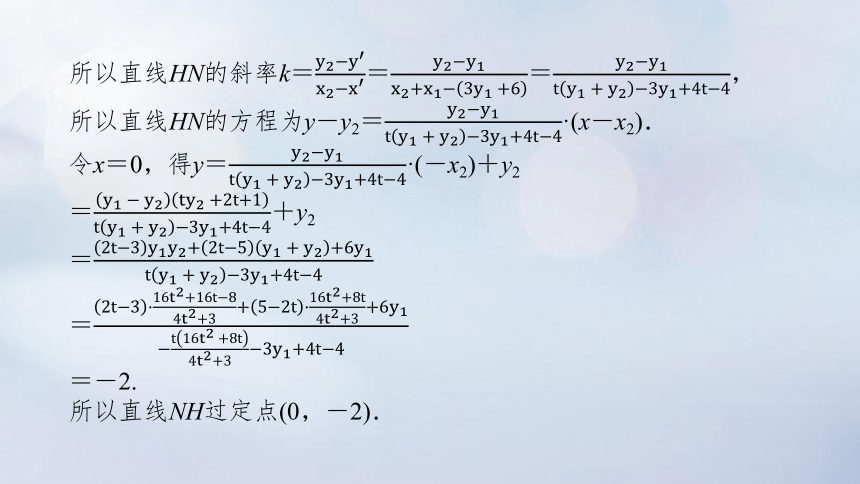




文档简介
(共54张PPT)
第3讲 圆锥曲线的综合问题
考点一
考点二
考点三
考点四
考点一 证明问题
——等价转化,直击目标
考点一 证明问题——等价转化,直击目标
圆锥曲线中证明问题的两种常见类型
圆锥曲线中的证明问题,主要有两类:一是证明点、直线、曲线等几何元素中的位置关系,如:某点在某直线上,某直线经过某个点、某两条直线平行或垂直等;二是证明直线与圆锥曲线中的一些数量关系(相等或不等).
例 1 [2022·全国乙卷]已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过A(0,-2),B(,-1)两点.
(1)求E的方程;
(2)设过点P(1,-2)的直线交E于M,N两点,过M且平行于x轴的直线与线段AB交于点T,点H满足=.证明:直线HN过定点.
解析:(1)设椭圆E的方程为mx2+ny2=1(m>0,n>0,m≠n).
将点A(0,-2),B(,-1)的坐标代入,得解得
所以椭圆E的方程为=1.
(2)证明:方法一 设M(x1,y1),N(x2,y2).
由题意,知直线MN与y轴不垂直,设其方程为x-1=t(y+2).
联立得方程组
消去x并整理,得(4t2+3)y2+(16t2+8t)y+16t2+16t-8=0,
所以y1+y2=-,y1y2=.
设T(x0,y1).由A,B,T三点共线,得=,得x0=y1+3.设H(x′,y′).
由=,得(y1+3-x1,0)=(x′-y1-3,y′-y1),所以x′=3y1+6-x1,y′=y1,
所以直线HN的斜率k===,
所以直线HN的方程为y-y2=·(x-x2).
令x=0,得y=·(-x2)+y2
=+y2
=
=
=-2.
所以直线NH过定点(0,-2).
方法二 由A(0,-2),B(,-1)可得直线AB的方程为y=x-2.
a.若过点P(1,-2)的直线的斜率不存在,则其直线方程为x=1.将直线方程x=1代入=1,可得N(1,),M(1,-).
将y=-代入y=x-2,可得T(3-,-).
由=,得H(5-2,-).
此时直线HN的方程为y=(2+)(x-1)+,
则直线HN过定点(0,-2).
b.若过点P(1,-2)的直线的斜率存在,设此直线方程为kx-y-(k+2)=0,M(x1,y1),N(x2,y2).
联立得方程组
消去y并整理,得(3k2+4)x2-6k(2+k)x+3k(k+4)=0.
所以则
且x1y2+x2y1=.①
联立得方程组,可得T(+3,y1).
由=,得H(3y1+6-x1,y1).
则直线HN的方程为y-y2=(x-x2).
将点(0,-2)的坐标代入并整理,得2(x1+x2)-6(y1+y2)+x1y2+x2y1-3y1y2-12=0.②
将①代入②,得24k+12k2+96+48k-24k-48-48k+24k2-36k2-48=0,显然成立.
综上可得,直线HN过定点(0,-2).
归纳总结
圆锥曲线中证明题的求解策略
处理圆锥曲线中的证明问题常采用直接法证明,证明时常借助于等价转化思想,化几何关系为数量关系,然后借助函数方程思想、数形结合思想解决.
对点训练
[2022·河南省淮阳中学模拟]已知直线y=3与曲线C:x2+2py=0的两个公共点之间的距离为4.
(1)求C的方程;
(2)设P为C的准线上一点,过P作C的两条切线,切点为A,B,直线PA,PB的斜率分别为k1,k2,且直线PA,PB与y轴分别交于M,N两点,直线AB的斜率为k0.证明:k1·k2为定值,且k1,k0,k2成等差数列.
解析:(1)将y=3代入x2+2py=0,得x2=-6p.
当p≥0时,不合题意;
当p<0时,x=±,则2=4,
解得p=-4,故C的方程为x2=8y.
(2)证明:由(1)可知C的准线方程为y=-2,
不妨设P(m,-2),A(x1,y1),B(x2,y2),
设过点P且与C相切的直线l的斜率为k,则l:y=k(x-m)-2,且k≠0,
联立得x2-8kx+8(km+2)=0,
则Δ=64k2-32(km+2)=0,即k2-mk-1=0,
由题意知,直线PA,PB的斜率k1,k2为方程k2-mk-1=0的两根,
则k1+k2=,k1k2=-1,故k1·k2为定值.
又x2-8kx+8(km+2)=(x-4k)2=0,
则x1=4k1,同理可得x2=4k2,
则k0===,
因此k0==,故k1,k0,k2成等差数列.
考点二 定点问题
——目标等式寻定点
考点二 定点问题——目标等式寻定点
解析几何中的定点问题一般是指与解析几何有关的直线或圆(其他曲线过定点太复杂,高中阶段一般不涉及)过定点的问题,其实质是:当动直线或动圆变化时,这些直线或圆相交于一点,即这些直线或圆绕着定点在转动,这类问题的求解一般分为以下三步:
一选:选择变量,定点问题中的定点,随某一个量的变化而固定,可选择这个量为变量(有时可选择两个变量,如点的坐标、斜率、截距等,然后利用其他辅助条件消去其中之一).
二求:求出定点坐标所满足的方程,即把需要证明为定点的问题表示成关于上述变量的方程.
三定点:对上述方程进行必要的化简,即可得到定点坐标.
例 2 [2022·青海海东市第一中学]已知椭圆M:=1(a>b>0)的离心率为,AB为过椭圆右焦点的一条弦,且AB长度的最小值为2.
(1)求椭圆M的方程;
(2)若直线l与椭圆M交于C,D两点,点P(2,0),记直线PC的斜率为k1,直线PD的斜率为k2,当=1时,是否存在直线l恒过一定点?若存在,请求出这个定点;若不存在,请说明理由.
解析:(1)因为=1(a>b>0)的离心率为,过椭圆右焦点的弦长的最小值为=2,
所以a=2,c=,b=,所以椭圆M的方程为=1.
(2)设直线l的方程为m(x-2)+ny=1,C(x1,y1),D(x2,y2),
由椭圆的方程x2+2y2=4,得(x-2)2+2y2=-4(x-2).
联立直线l的方程与椭圆方程,得(x-2)2+2y2=-4(x-2)[m(x-2)+ny],
即(1+4m)(x-2)2+4n(x-2)y+2y2=0,
(1+4m)2+4n+2=0,
所以==-=1,
化简得m+n=-,代入直线l的方程得m(x-2)+y=1,
即m(x-y-2)-y=1,解得x=-2,y=-4,即直线l恒过定点(-2,-4).
归纳总结
直线过定点问题的解题策略
对点训练
[2022·河南开封二模]已知抛物线C:y2=2px(p>0)的焦点为F,S(t,4)为C上一点,直线l交C于M,N两点(与点S不重合).
(1)若l过点F且倾斜角为60°,=4(M在第一象限),求C的方程;
(2)若p=2,直线SM,SN分别与y轴交于A,B两点,且·=8,判断直线l是否恒过定点?若是,求出该定点;若否,请说明理由.
解析:(1)抛物线C:y2=2px(p>0)的焦点为F(,0),
因为l过点F且倾斜角为60°,所以l:y=(x-),
联立y2=2px(p>0),可得12x2-20px+3p2=0,解得x=p或x=,
又M在第一象限,所以xM=p,
因为=4,所以p+=4,解得p=2,
所以抛物线C的方程为y2=4x;
(2)由已知可得抛物线C的方程为y2=4x,点S(4,4),
设直线l的方程为x=my+n,点,
将直线l的方程与抛物线C:y2=4x联立得y2-4my-4n=0,
所以Δ=16m2+16n>0,y1+y2=4m,y1y2=-4n(*),
直线SM的方程为y-4=(x-4),
令x=0求得点A的纵坐标为,同理求得点B的纵坐标为,
由·==8,化简得y1y2=4(y1+y2)+16,
将上面(*)式代入得-4n=16m+16,即n=-4m-4,
所以直线l的方程为x=my-4m-4,即x+4=m(y-4),
所以直线l过定点(-4,4).
考点三 定值问题
——巧妙消元寻定值
考点三 定值问题——巧妙消元寻定值
定值问题一般是指在求解解析几何问题的过程中,探究某些几何量(斜率、距离、面积、比值等)与变量(斜率、点的坐标等)无关的问题,其求解步骤一般为:
一选:选择变量,一般为点的坐标、直线的斜率等.
二化:把要求解的定值表示成含上述变量的式子,并利用其他辅助条件来减少变量的个数,使其只含有一个变量(或者有多个变量,若是能整体约分也可以).
三定值:化简式子得到定值.由题目的结论可知要证明为定值的量必与变量的值无关,故求出的式子必能化为一个常数,所以只需对上述式子进行必要的化简即可得到定值.
例 3 [2022·山东潍坊模拟]已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1、F2,双曲线C的右顶点A在圆O:x2+y2=3上,且=-1.
(1)求双曲线C的方程;
(2)动直线l与双曲线C恰有1个公共点,且与双曲线C的两条渐近线分别交于点M、N,设O为坐标原点.求证:△OMN的面积为定值.
解析:(1)不妨设F1(-c,0),F2(c,0), 因为A(a,0),
从而==(c-a,0) ,故有=a2-c2=-1,
又因为a2+b2=c2, 所以 b=1,
又因为A(a,0) 在圆 O:x2+y2=3 上, 所以 a=,
所以双曲线C的标准方程为-y2=1.
(2)证明:设直线l与x轴交于D点,双曲线的渐近线方程为y=±x,
由于动直线l与双曲线C恰有1个公共点, 且与双曲线C的两条渐近线分别交于点M、N,
当动直线l的斜率不存在时, l:x=±==2,S△OMN=×2=,
当动直线l的斜率存在时, 且斜率k≠±, 不妨设直线 l:y=kx+m,
故由 (1-3k2)x2-6mkx-3m2-3=0,
依题意,1-3k2≠0且m≠0,
Δ=(-6mk)2-4(1-3k2)(-3m2-3)=0, 化简得 3k2=m2+1,
故由 xM=, 同理可求,xN=-,
所以==,
又因为原点O到直线l:kx-y+m=0的距离d=,
所以S△OMN=d=,又由3k2=m2+1,所以S△OMN==,故△OMN的面积为定值,定值为.
归纳总结
求解圆锥曲线中定值问题常用的方法
(1)引出变量法.解题流程为:
(2)特殊法.从特殊入手,求出定值,再证明这个值与变量无关.
(3)直接法.直接推理,在计算过程中消去变量,从而得到定值.
对点训练
已知F1(-,0),F2(,0)分别是双曲线C:=1(a>b>0)的左、右焦点,A为双曲线在第一象限的点,△AF1F2的内切圆与x轴交于点P(1,0).
(1)求双曲线C的方程;
(2)设圆O:x2+y2=2上任意一点Q处的切线l,若l与双曲线C左、右两支分别交于点M、N,问:·是否为定值?若是,求出此定值;若不是,说明理由.
解析:(1)如图,设AF1,AF2与△AF1F2的内切圆分别交于G,H两点,
则2a==
=(1+)-(-1)=2,
所以a=1,则b2=c2-a2=2,
则双曲线C的方程为x2-=1.
(2)由题意得,切线l的斜率存在.
设切线l的方程为y=kx+m,M(x1,y1),N(x2,y2).
因为l与圆O:x2+y2=2相切,所以=,即m2=2k2+2.
联立消去y并整理得(2-k2)x2-2kmx-m2-2=0,
所以x1+x2=,x1x2=.
又·=()·()
=2-···
=2-·cos ∠QON-·cos ∠QOM+·
=2-···
=2-2-2+·=·.
又·=x1x2+y1y2
=x1x2+(kx1+m)(kx2+m)
=(k2+1)x1x2+km(x1+x2)+m2
=+m2
=,
将m2=2k2+2代入上式得·=0.
所以·=0-||2=-2.
综上所述,·为定值,且·=-2.
考点四 圆锥曲线中的最值、范围问题
——巧设变量,引参搭桥
考点四 圆锥曲线中的最值、范围问题——巧设变量,引参搭桥
圆锥曲线中的最值
(1)椭圆中的最值
F1,F2为椭圆=1(a>b>0)的左、右焦点,P为椭圆上的任意一点,B为短轴的一个端点,O为坐标原点,则有:
①|OP|∈______;②|PF1|∈__________;·|PF2|∈________;④∠F1PF2≤∠F1BF2.
(2)双曲线中的最值
F1,F2为双曲线=1(a>0,b>0)的左、右焦点,P为双曲线上的任一点,O为坐标原点,则有:
①|OP|≥________;②|PF1|≥________.
[b,a]
[a-c,a+c]
[b2,a2]
a
c-a
(3)抛物线中的最值
点P为抛物线y2=2px(p>0)上的任一点,F为焦点,则有:
①|PF|≥________;②A(m,n)为一定点,则|PA|+|PF|有最小值;③点N(a,0)是抛物线的对称轴上一点,则|PN|min=
例 4 [2022·浙江卷]如图,已知椭圆+y2=1.设A,B是椭圆上异于P(0,1)的两点,且点Q(0,)在线段AB上,直线PA,PB分别交直线y=-x+3于C,D两点.
(1)求点P到椭圆上点的距离的最大值;
(2)求|CD|的最小值.
解析:(1)设M(2cos θ,sin θ)是椭圆上一点,P(0,1),
则|PM|2=12cos2θ+(1-sinθ)2=13-11sin2θ-2sinθ=-11(sin θ+)2≤.
故|PM|的最大值为.
(2)由题意,知直线AB的斜率存在,
故设直线AB的方程为y=kx+.
将直线方程与椭圆方程联立,得
消去y并整理,得(k2+)x2+kx-=0.
设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=-.
直线PA:y=x+1与直线y=-x+3交于点C,则xC==.
同理可得,xD==,
则|CD|= |xC-xD|=||
=2||=2||
=·=·≥,
当且仅当k=时等号成立.故|CD|的最小值为.
归纳总结
1.圆锥曲线中的最值问题的求解方法
(1)几何法:题中给出的条件有明显的几何特征,则考虑用几何性质来解决,特别要注意用圆锥曲线的定义和平面几何有关结论来求最值.
(2)代数法:题中给出的条件和结论的几何特征不明显,则考虑先建立目标函数(通常为二次函数),再求这个函数的最值.求函数的最值常见的方法有配方法、基本不等式法、单调性法、三角换元法等.
2.圆锥曲线中的取值范围问题的5种常用解法
(1)利用圆锥曲线的几何性质或判别式构造不等关系.从而确定参数的取值范围.
(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系.
(3)利用隐含的不等关系建立不等式,从而求出参数的取值范围.
(4)利用已知的不等关系构造不等式,从而求出参数的取值范围.
(5)利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.
对点训练
[2021·全国乙卷]已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.
(1)求p;
(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求△PAB面积的最大值.
解析:(1)由题意知M(0,-4),F,圆M的半径r=1,所以|MF|-r=4,即+4-1=4,解得p=2.
(2)由(1)知,抛物线方程为x2=4y,
由题意可知直线AB的斜率存在,设,直线AB的方程为y=kx+b,
联立得,消去y得x2-4kx-4b=0,
则Δ=16k2+16b>0(※),x1+x2=4k,x1x2=-4b,
所以|AB|=|x1-x2|=·=4·.
因为x2=4y,即y=,所以y′=,则抛物线在点A处的切线斜率为,在点A处的切线方程为=(x-x1),即y=,
同理得抛物线在点B处的切线方程为y=,
联立得,则,
即P(2k,-b).因为点P在圆M上,所以4k2+(4-b)2=1 ①,
且-1≤2k≤1,-5≤-b≤-3,即-≤k≤,3≤b≤5,满足(※).
设点P到直线AB的距离为d,则d=,
所以S△PAB=|AB|·d=4.
由①得,k2==,
令t=k2+b,则t=,且3≤b≤5.
因为t=在[3,5]上单调递增,所以当b=5时,t取得最大值,tmax=5,此时k=0,所以△PAB面积的最大值为20.
[高考5个大题] 解题研诀窍(五) 解析几何类解答题
[思维流程——圆锥曲线问题重在“设”与“算”]
[技法指导——迁移搭桥]
数学思想是问题的主线,方法是解题的手段,审视方法,选择适当的解题方法,往往使问题的解决事半功倍,审题的过程还是一个解题方法的抉择过程,开拓的解题思路能使我们心涌如潮,适宜的解题方法则帮助我们事半功倍.
[典例] 已知圆(x+)2+y2=16的圆心为M,点P是圆M上的动点,点N(,0),点G在线段MP上,且满足()⊥().
(1)求点G的轨迹C的方程;
(2)过点T(4,0)作斜率不为0的直线l与轨迹C交于A,B两点,点A关于x轴的对称点为D,连接BD交x轴于点Q,求△ABQ面积的最大值.
[快审题]
求什么 想什么 求轨迹方程,想到求轨迹方程的方法.
求三角形面积的最值,想到表示出三角形面积的式子.
给什么 用什么 给出向量垂直关系,用数量积转化为线段相等.
给出直线l的条件,应设出直线方程,与C的方程联立方程组.
差什么 找什么 差三角形的高,应先找Q点的坐标,即求出BD的直线方程.
[稳解题]
(1)因为()⊥(),
所以()·()=0,即-=0,
所以|GP|=|GN|,
所以|GM|+|GN|=|GM|+|GP|=|MP|=4>2=|MN|,
所以点G在以M,N为焦点,长轴长为4的椭圆上,
设椭圆的方程为=1(a>b>0),
则2a=4,2c=2,
即a=2,c=,所以b2=a2-c2=1,
所以点G的轨迹C的方程为+y2=1.
(2)
依题意可设直线l:x=my+4.
由消去x,得(m2+4)y2+8my+12=0.
设A(x1,y1),B(x2,y2),
由Δ=64m2-4×12×(m2+4)=16(m2-12)>0,得>12. ①
且y1+y2=-,
y1y2=. ②
因为点A关于x轴的对称点为D,
所以D(x1,-y1),
可设Q(x0,0),
所以kBD==,
所以BD所在直线的方程为y-y2=(x-my2-4).
令y=0,得x0=. ③
将②代入③,
得x0==1,
所以点Q的坐标为(1,0).
因为S△ABQ=|S△TBQ-S△TAQ|
=|QT||y2-y1|==,
令t=m2+4,结合①得t>16,
所以S△ABQ==
6=6.
当且仅当t=32,即m=±2时,(S△ABQ)max=.
所以△ABQ面积的最大值为.
题后悟道
解决直线与圆锥曲线位置关系问题的步骤
第3讲 圆锥曲线的综合问题
考点一
考点二
考点三
考点四
考点一 证明问题
——等价转化,直击目标
考点一 证明问题——等价转化,直击目标
圆锥曲线中证明问题的两种常见类型
圆锥曲线中的证明问题,主要有两类:一是证明点、直线、曲线等几何元素中的位置关系,如:某点在某直线上,某直线经过某个点、某两条直线平行或垂直等;二是证明直线与圆锥曲线中的一些数量关系(相等或不等).
例 1 [2022·全国乙卷]已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过A(0,-2),B(,-1)两点.
(1)求E的方程;
(2)设过点P(1,-2)的直线交E于M,N两点,过M且平行于x轴的直线与线段AB交于点T,点H满足=.证明:直线HN过定点.
解析:(1)设椭圆E的方程为mx2+ny2=1(m>0,n>0,m≠n).
将点A(0,-2),B(,-1)的坐标代入,得解得
所以椭圆E的方程为=1.
(2)证明:方法一 设M(x1,y1),N(x2,y2).
由题意,知直线MN与y轴不垂直,设其方程为x-1=t(y+2).
联立得方程组
消去x并整理,得(4t2+3)y2+(16t2+8t)y+16t2+16t-8=0,
所以y1+y2=-,y1y2=.
设T(x0,y1).由A,B,T三点共线,得=,得x0=y1+3.设H(x′,y′).
由=,得(y1+3-x1,0)=(x′-y1-3,y′-y1),所以x′=3y1+6-x1,y′=y1,
所以直线HN的斜率k===,
所以直线HN的方程为y-y2=·(x-x2).
令x=0,得y=·(-x2)+y2
=+y2
=
=
=-2.
所以直线NH过定点(0,-2).
方法二 由A(0,-2),B(,-1)可得直线AB的方程为y=x-2.
a.若过点P(1,-2)的直线的斜率不存在,则其直线方程为x=1.将直线方程x=1代入=1,可得N(1,),M(1,-).
将y=-代入y=x-2,可得T(3-,-).
由=,得H(5-2,-).
此时直线HN的方程为y=(2+)(x-1)+,
则直线HN过定点(0,-2).
b.若过点P(1,-2)的直线的斜率存在,设此直线方程为kx-y-(k+2)=0,M(x1,y1),N(x2,y2).
联立得方程组
消去y并整理,得(3k2+4)x2-6k(2+k)x+3k(k+4)=0.
所以则
且x1y2+x2y1=.①
联立得方程组,可得T(+3,y1).
由=,得H(3y1+6-x1,y1).
则直线HN的方程为y-y2=(x-x2).
将点(0,-2)的坐标代入并整理,得2(x1+x2)-6(y1+y2)+x1y2+x2y1-3y1y2-12=0.②
将①代入②,得24k+12k2+96+48k-24k-48-48k+24k2-36k2-48=0,显然成立.
综上可得,直线HN过定点(0,-2).
归纳总结
圆锥曲线中证明题的求解策略
处理圆锥曲线中的证明问题常采用直接法证明,证明时常借助于等价转化思想,化几何关系为数量关系,然后借助函数方程思想、数形结合思想解决.
对点训练
[2022·河南省淮阳中学模拟]已知直线y=3与曲线C:x2+2py=0的两个公共点之间的距离为4.
(1)求C的方程;
(2)设P为C的准线上一点,过P作C的两条切线,切点为A,B,直线PA,PB的斜率分别为k1,k2,且直线PA,PB与y轴分别交于M,N两点,直线AB的斜率为k0.证明:k1·k2为定值,且k1,k0,k2成等差数列.
解析:(1)将y=3代入x2+2py=0,得x2=-6p.
当p≥0时,不合题意;
当p<0时,x=±,则2=4,
解得p=-4,故C的方程为x2=8y.
(2)证明:由(1)可知C的准线方程为y=-2,
不妨设P(m,-2),A(x1,y1),B(x2,y2),
设过点P且与C相切的直线l的斜率为k,则l:y=k(x-m)-2,且k≠0,
联立得x2-8kx+8(km+2)=0,
则Δ=64k2-32(km+2)=0,即k2-mk-1=0,
由题意知,直线PA,PB的斜率k1,k2为方程k2-mk-1=0的两根,
则k1+k2=,k1k2=-1,故k1·k2为定值.
又x2-8kx+8(km+2)=(x-4k)2=0,
则x1=4k1,同理可得x2=4k2,
则k0===,
因此k0==,故k1,k0,k2成等差数列.
考点二 定点问题
——目标等式寻定点
考点二 定点问题——目标等式寻定点
解析几何中的定点问题一般是指与解析几何有关的直线或圆(其他曲线过定点太复杂,高中阶段一般不涉及)过定点的问题,其实质是:当动直线或动圆变化时,这些直线或圆相交于一点,即这些直线或圆绕着定点在转动,这类问题的求解一般分为以下三步:
一选:选择变量,定点问题中的定点,随某一个量的变化而固定,可选择这个量为变量(有时可选择两个变量,如点的坐标、斜率、截距等,然后利用其他辅助条件消去其中之一).
二求:求出定点坐标所满足的方程,即把需要证明为定点的问题表示成关于上述变量的方程.
三定点:对上述方程进行必要的化简,即可得到定点坐标.
例 2 [2022·青海海东市第一中学]已知椭圆M:=1(a>b>0)的离心率为,AB为过椭圆右焦点的一条弦,且AB长度的最小值为2.
(1)求椭圆M的方程;
(2)若直线l与椭圆M交于C,D两点,点P(2,0),记直线PC的斜率为k1,直线PD的斜率为k2,当=1时,是否存在直线l恒过一定点?若存在,请求出这个定点;若不存在,请说明理由.
解析:(1)因为=1(a>b>0)的离心率为,过椭圆右焦点的弦长的最小值为=2,
所以a=2,c=,b=,所以椭圆M的方程为=1.
(2)设直线l的方程为m(x-2)+ny=1,C(x1,y1),D(x2,y2),
由椭圆的方程x2+2y2=4,得(x-2)2+2y2=-4(x-2).
联立直线l的方程与椭圆方程,得(x-2)2+2y2=-4(x-2)[m(x-2)+ny],
即(1+4m)(x-2)2+4n(x-2)y+2y2=0,
(1+4m)2+4n+2=0,
所以==-=1,
化简得m+n=-,代入直线l的方程得m(x-2)+y=1,
即m(x-y-2)-y=1,解得x=-2,y=-4,即直线l恒过定点(-2,-4).
归纳总结
直线过定点问题的解题策略
对点训练
[2022·河南开封二模]已知抛物线C:y2=2px(p>0)的焦点为F,S(t,4)为C上一点,直线l交C于M,N两点(与点S不重合).
(1)若l过点F且倾斜角为60°,=4(M在第一象限),求C的方程;
(2)若p=2,直线SM,SN分别与y轴交于A,B两点,且·=8,判断直线l是否恒过定点?若是,求出该定点;若否,请说明理由.
解析:(1)抛物线C:y2=2px(p>0)的焦点为F(,0),
因为l过点F且倾斜角为60°,所以l:y=(x-),
联立y2=2px(p>0),可得12x2-20px+3p2=0,解得x=p或x=,
又M在第一象限,所以xM=p,
因为=4,所以p+=4,解得p=2,
所以抛物线C的方程为y2=4x;
(2)由已知可得抛物线C的方程为y2=4x,点S(4,4),
设直线l的方程为x=my+n,点,
将直线l的方程与抛物线C:y2=4x联立得y2-4my-4n=0,
所以Δ=16m2+16n>0,y1+y2=4m,y1y2=-4n(*),
直线SM的方程为y-4=(x-4),
令x=0求得点A的纵坐标为,同理求得点B的纵坐标为,
由·==8,化简得y1y2=4(y1+y2)+16,
将上面(*)式代入得-4n=16m+16,即n=-4m-4,
所以直线l的方程为x=my-4m-4,即x+4=m(y-4),
所以直线l过定点(-4,4).
考点三 定值问题
——巧妙消元寻定值
考点三 定值问题——巧妙消元寻定值
定值问题一般是指在求解解析几何问题的过程中,探究某些几何量(斜率、距离、面积、比值等)与变量(斜率、点的坐标等)无关的问题,其求解步骤一般为:
一选:选择变量,一般为点的坐标、直线的斜率等.
二化:把要求解的定值表示成含上述变量的式子,并利用其他辅助条件来减少变量的个数,使其只含有一个变量(或者有多个变量,若是能整体约分也可以).
三定值:化简式子得到定值.由题目的结论可知要证明为定值的量必与变量的值无关,故求出的式子必能化为一个常数,所以只需对上述式子进行必要的化简即可得到定值.
例 3 [2022·山东潍坊模拟]已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1、F2,双曲线C的右顶点A在圆O:x2+y2=3上,且=-1.
(1)求双曲线C的方程;
(2)动直线l与双曲线C恰有1个公共点,且与双曲线C的两条渐近线分别交于点M、N,设O为坐标原点.求证:△OMN的面积为定值.
解析:(1)不妨设F1(-c,0),F2(c,0), 因为A(a,0),
从而==(c-a,0) ,故有=a2-c2=-1,
又因为a2+b2=c2, 所以 b=1,
又因为A(a,0) 在圆 O:x2+y2=3 上, 所以 a=,
所以双曲线C的标准方程为-y2=1.
(2)证明:设直线l与x轴交于D点,双曲线的渐近线方程为y=±x,
由于动直线l与双曲线C恰有1个公共点, 且与双曲线C的两条渐近线分别交于点M、N,
当动直线l的斜率不存在时, l:x=±==2,S△OMN=×2=,
当动直线l的斜率存在时, 且斜率k≠±, 不妨设直线 l:y=kx+m,
故由 (1-3k2)x2-6mkx-3m2-3=0,
依题意,1-3k2≠0且m≠0,
Δ=(-6mk)2-4(1-3k2)(-3m2-3)=0, 化简得 3k2=m2+1,
故由 xM=, 同理可求,xN=-,
所以==,
又因为原点O到直线l:kx-y+m=0的距离d=,
所以S△OMN=d=,又由3k2=m2+1,所以S△OMN==,故△OMN的面积为定值,定值为.
归纳总结
求解圆锥曲线中定值问题常用的方法
(1)引出变量法.解题流程为:
(2)特殊法.从特殊入手,求出定值,再证明这个值与变量无关.
(3)直接法.直接推理,在计算过程中消去变量,从而得到定值.
对点训练
已知F1(-,0),F2(,0)分别是双曲线C:=1(a>b>0)的左、右焦点,A为双曲线在第一象限的点,△AF1F2的内切圆与x轴交于点P(1,0).
(1)求双曲线C的方程;
(2)设圆O:x2+y2=2上任意一点Q处的切线l,若l与双曲线C左、右两支分别交于点M、N,问:·是否为定值?若是,求出此定值;若不是,说明理由.
解析:(1)如图,设AF1,AF2与△AF1F2的内切圆分别交于G,H两点,
则2a==
=(1+)-(-1)=2,
所以a=1,则b2=c2-a2=2,
则双曲线C的方程为x2-=1.
(2)由题意得,切线l的斜率存在.
设切线l的方程为y=kx+m,M(x1,y1),N(x2,y2).
因为l与圆O:x2+y2=2相切,所以=,即m2=2k2+2.
联立消去y并整理得(2-k2)x2-2kmx-m2-2=0,
所以x1+x2=,x1x2=.
又·=()·()
=2-···
=2-·cos ∠QON-·cos ∠QOM+·
=2-···
=2-2-2+·=·.
又·=x1x2+y1y2
=x1x2+(kx1+m)(kx2+m)
=(k2+1)x1x2+km(x1+x2)+m2
=+m2
=,
将m2=2k2+2代入上式得·=0.
所以·=0-||2=-2.
综上所述,·为定值,且·=-2.
考点四 圆锥曲线中的最值、范围问题
——巧设变量,引参搭桥
考点四 圆锥曲线中的最值、范围问题——巧设变量,引参搭桥
圆锥曲线中的最值
(1)椭圆中的最值
F1,F2为椭圆=1(a>b>0)的左、右焦点,P为椭圆上的任意一点,B为短轴的一个端点,O为坐标原点,则有:
①|OP|∈______;②|PF1|∈__________;·|PF2|∈________;④∠F1PF2≤∠F1BF2.
(2)双曲线中的最值
F1,F2为双曲线=1(a>0,b>0)的左、右焦点,P为双曲线上的任一点,O为坐标原点,则有:
①|OP|≥________;②|PF1|≥________.
[b,a]
[a-c,a+c]
[b2,a2]
a
c-a
(3)抛物线中的最值
点P为抛物线y2=2px(p>0)上的任一点,F为焦点,则有:
①|PF|≥________;②A(m,n)为一定点,则|PA|+|PF|有最小值;③点N(a,0)是抛物线的对称轴上一点,则|PN|min=
例 4 [2022·浙江卷]如图,已知椭圆+y2=1.设A,B是椭圆上异于P(0,1)的两点,且点Q(0,)在线段AB上,直线PA,PB分别交直线y=-x+3于C,D两点.
(1)求点P到椭圆上点的距离的最大值;
(2)求|CD|的最小值.
解析:(1)设M(2cos θ,sin θ)是椭圆上一点,P(0,1),
则|PM|2=12cos2θ+(1-sinθ)2=13-11sin2θ-2sinθ=-11(sin θ+)2≤.
故|PM|的最大值为.
(2)由题意,知直线AB的斜率存在,
故设直线AB的方程为y=kx+.
将直线方程与椭圆方程联立,得
消去y并整理,得(k2+)x2+kx-=0.
设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=-.
直线PA:y=x+1与直线y=-x+3交于点C,则xC==.
同理可得,xD==,
则|CD|= |xC-xD|=||
=2||=2||
=·=·≥,
当且仅当k=时等号成立.故|CD|的最小值为.
归纳总结
1.圆锥曲线中的最值问题的求解方法
(1)几何法:题中给出的条件有明显的几何特征,则考虑用几何性质来解决,特别要注意用圆锥曲线的定义和平面几何有关结论来求最值.
(2)代数法:题中给出的条件和结论的几何特征不明显,则考虑先建立目标函数(通常为二次函数),再求这个函数的最值.求函数的最值常见的方法有配方法、基本不等式法、单调性法、三角换元法等.
2.圆锥曲线中的取值范围问题的5种常用解法
(1)利用圆锥曲线的几何性质或判别式构造不等关系.从而确定参数的取值范围.
(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系.
(3)利用隐含的不等关系建立不等式,从而求出参数的取值范围.
(4)利用已知的不等关系构造不等式,从而求出参数的取值范围.
(5)利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.
对点训练
[2021·全国乙卷]已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.
(1)求p;
(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求△PAB面积的最大值.
解析:(1)由题意知M(0,-4),F,圆M的半径r=1,所以|MF|-r=4,即+4-1=4,解得p=2.
(2)由(1)知,抛物线方程为x2=4y,
由题意可知直线AB的斜率存在,设,直线AB的方程为y=kx+b,
联立得,消去y得x2-4kx-4b=0,
则Δ=16k2+16b>0(※),x1+x2=4k,x1x2=-4b,
所以|AB|=|x1-x2|=·=4·.
因为x2=4y,即y=,所以y′=,则抛物线在点A处的切线斜率为,在点A处的切线方程为=(x-x1),即y=,
同理得抛物线在点B处的切线方程为y=,
联立得,则,
即P(2k,-b).因为点P在圆M上,所以4k2+(4-b)2=1 ①,
且-1≤2k≤1,-5≤-b≤-3,即-≤k≤,3≤b≤5,满足(※).
设点P到直线AB的距离为d,则d=,
所以S△PAB=|AB|·d=4.
由①得,k2==,
令t=k2+b,则t=,且3≤b≤5.
因为t=在[3,5]上单调递增,所以当b=5时,t取得最大值,tmax=5,此时k=0,所以△PAB面积的最大值为20.
[高考5个大题] 解题研诀窍(五) 解析几何类解答题
[思维流程——圆锥曲线问题重在“设”与“算”]
[技法指导——迁移搭桥]
数学思想是问题的主线,方法是解题的手段,审视方法,选择适当的解题方法,往往使问题的解决事半功倍,审题的过程还是一个解题方法的抉择过程,开拓的解题思路能使我们心涌如潮,适宜的解题方法则帮助我们事半功倍.
[典例] 已知圆(x+)2+y2=16的圆心为M,点P是圆M上的动点,点N(,0),点G在线段MP上,且满足()⊥().
(1)求点G的轨迹C的方程;
(2)过点T(4,0)作斜率不为0的直线l与轨迹C交于A,B两点,点A关于x轴的对称点为D,连接BD交x轴于点Q,求△ABQ面积的最大值.
[快审题]
求什么 想什么 求轨迹方程,想到求轨迹方程的方法.
求三角形面积的最值,想到表示出三角形面积的式子.
给什么 用什么 给出向量垂直关系,用数量积转化为线段相等.
给出直线l的条件,应设出直线方程,与C的方程联立方程组.
差什么 找什么 差三角形的高,应先找Q点的坐标,即求出BD的直线方程.
[稳解题]
(1)因为()⊥(),
所以()·()=0,即-=0,
所以|GP|=|GN|,
所以|GM|+|GN|=|GM|+|GP|=|MP|=4>2=|MN|,
所以点G在以M,N为焦点,长轴长为4的椭圆上,
设椭圆的方程为=1(a>b>0),
则2a=4,2c=2,
即a=2,c=,所以b2=a2-c2=1,
所以点G的轨迹C的方程为+y2=1.
(2)
依题意可设直线l:x=my+4.
由消去x,得(m2+4)y2+8my+12=0.
设A(x1,y1),B(x2,y2),
由Δ=64m2-4×12×(m2+4)=16(m2-12)>0,得>12. ①
且y1+y2=-,
y1y2=. ②
因为点A关于x轴的对称点为D,
所以D(x1,-y1),
可设Q(x0,0),
所以kBD==,
所以BD所在直线的方程为y-y2=(x-my2-4).
令y=0,得x0=. ③
将②代入③,
得x0==1,
所以点Q的坐标为(1,0).
因为S△ABQ=|S△TBQ-S△TAQ|
=|QT||y2-y1|==,
令t=m2+4,结合①得t>16,
所以S△ABQ==
6=6.
当且仅当t=32,即m=±2时,(S△ABQ)max=.
所以△ABQ面积的最大值为.
题后悟道
解决直线与圆锥曲线位置关系问题的步骤
同课章节目录
