(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题一三角函数与解三角形第1讲 三角函数的图象与性质 课件(40张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题一三角函数与解三角形第1讲 三角函数的图象与性质 课件(40张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 06:03:18 | ||
图片预览











文档简介
(共40张PPT)
第1讲 三角函数的图象与性质
考点一
考点二
考点三
考点四
考点一 三角函数的定义、诱导公式及基本关系
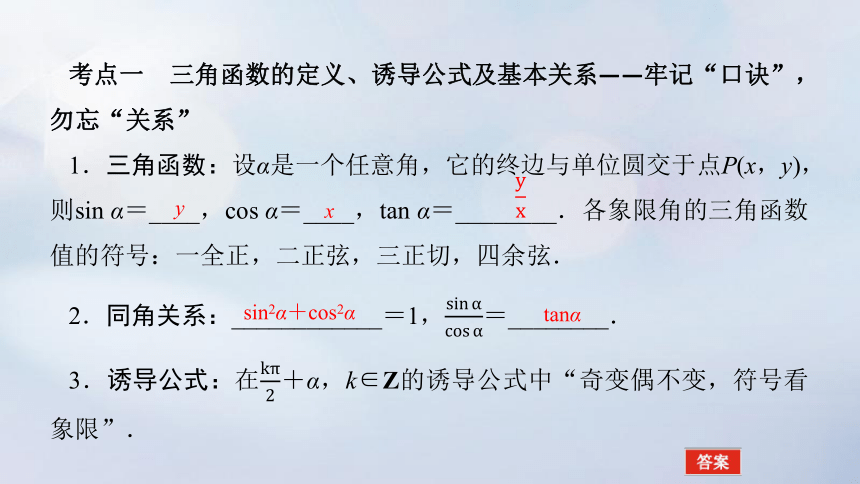
考点一 三角函数的定义、诱导公式及基本关系——牢记“口诀”,勿忘“关系”
1.三角函数:设α是一个任意角,它的终边与单位圆交于点P(x,y),则sin α=____,cos α=____,tan α=________.各象限角的三角函数值的符号:一全正,二正弦,三正切,四余弦.
2.同角关系:____________=1,=________.
3.诱导公式:在+α,k∈Z的诱导公式中“奇变偶不变,符号看象限”.
y
x
sin2α+cos2α
tanα
例 1 (1)[2022·湖南长沙一中模拟]若角α的终边过点P(8m,-3),且tan α=,则m的值为( )
A.- B.
C.- D.
答案:A
解析:∵tan α==,∴m=-,故选A.
(2)[2022·安徽蚌埠三模]已知tan α=2,则的值为( )
A.3 B.-3
C. D.-1
答案:A
解析:原式====3.故选A.
归纳总结
利用公式进行化简求值的策略
(1)利用诱导公式化任意角的三角函数为锐角三角函数,其步骤为:去负→脱周→化锐,特别注意函数名称和符号的确定.
(2)利用同角三角函数的关系化简过程要遵循一定的原则,如切化弦、化异为同、化高为低、化繁为简等.
提醒 使用三角函数诱导公式易错的地方有两个:一个是函数名称,一个是函数值的符号.
对点训练
1.[2022·河南新乡二模]已知点A是α的终边与单位圆的交点,若A的横坐标为-,则cos 2α=( )
A. B.-
C. D.-
答案:C
解析:由题意知,cos α=-,所以cos 2α=2cos2α-1=.故选C.
2.[2021·新高考Ⅰ卷]若tan θ=-2,则=( )
A.- B. -
C. D.
答案:C
解析:将式子进行齐次化处理得:
=
=sin θ====.故选C.
考点二
三角函数的图象与解析式
考点二 三角函数的图象与解析式
——平移看“ω,φ”,伸缩看“A,ω”,由图定式找对应,性质、图象结合牢
三角函数图象的变换
先平移后伸缩
先伸缩后平移
例 2 (1)[2022·山东烟台二中检测]若函数f(x)=sin (ωx-φ)的部分图象如图所示,则ω和φ的值是( )
A.ω=1,φ= B.ω=1,φ=-
C.ω=,φ=- D.ω=,φ=
答案:C
解析:由图象可知=,T=4π=,ω=,所以f(x)=sin ,f=sin =1,-φ=2kπ+,φ=-2kπ-(k∈Z),由于|φ|≤,所以φ=-.故选C.
(2)[2022·重庆模拟预测]已知曲线C:y=sin (ωx+φ)的部分图象如图所示,要得到曲线C的图象,可将曲线y=cos x的图象( )
A.先向右平移个单位长度,再将各点的横坐标
缩短到原来的倍,纵坐标不变
B.先向右平移个单位长度,再将各点的横坐标
伸长到原来的2倍,纵坐标不变
C.先向左平移个单位长度,再将各点的横坐标
缩短到原来的倍,纵坐标不变
D.先向左平移个单位长度,再将各点的横坐标伸长到原来的2倍,纵坐标不变
答案:A
解析:因为y=sin (ωx+φ)函数过点,即sin φ=,又|φ|<,所以φ=,即y=sin ,又函数过点,根据五点作图法可知ω+=π,解得ω=2,所以y=sin =sin =cos ,
由y=cos x向右平移个单位长度得到y=cos ,再将y=cos 各点的横坐标缩短到原来的倍,纵坐标不变得到y=cos ,即y=sin .故选A.
归纳总结
由三角函数的图象求解析式y=A sin (ωx+φ)+B(A>0,ω>0)中参数的值.
(1)最值定A,B:根据给定的函数图象确定最值,设最大值为M,最小值为m,则M=A+B,m=-A+B,解得B=,A=.
(2)T定ω:由周期的求解公式T=,可得ω=.
(3)特殊点定φ:代入特殊点求φ,一般代最高点或最低点,代入中心点时应注意是上升趋势还是下降趋势.
提醒 在图象变换过程中务必分清是先相位变换,还是先周期变换.变换只是相对于其中的自变量x而言的,如果x的系数不是1,就要把这个系数提取后再确定变换的单位长度和方向.
对点训练
1.[2021·全国甲卷]已知函数f(x)=2cos (ωx+φ)的部分图象如图所示,则f=________.
-
解析:方法一(五点作图法) 由题图可知T==(T为f(x)的最小正周期),即T=π,所以=π,即ω=2,故f(x)=2cos (2x+φ).点可看作“五点作图法”中的第二个点,故2×+φ=,得φ=-,即f(x)=2cos ,所以f=2cos =-.
方法二(代点法) 由题意知,T==(T为f(x)的最小正周期),所以T=π,=π,即ω=2.又因为点在函数f(x)的图象上,所以2cos =0,所以2×+φ=+kπ(k∈Z),令k=0,则φ=-,所以f(x)=2cos ,所以f=2cos =-2cos =-.
方法三(平移法) 由题意知,T==(T为f(x)的最小正周期),所以T=π,=π,即ω=2.函数y=2cos 2x的图象与x轴的一个交点是,对应函数f(x)=2cos (2x+φ)的图象与x轴的一个交点是,所以f(x)=2cos (2x+φ)的图象是由y=2cos 2x的图象向右平移=个单位长度得到的,所以f(x)=2cos (2x+φ)=2cos 2=2cos ,所以f=2cos =-2cos =-.
2.[2022·四川南充二模]函数f(x)=A sin (2x+θ)的部分图象如图所示,f(0)=,则( )
A.f(x)关于点对称
B.f(x)关于直线x=对称
C.f(x)在上单调递减
D.f(x)在上单调递增
答案:C
解析:由图可知A=2,且f(0)=,所以f(0)=2sin θ=,即sin θ=,因为|θ|≤,所以θ=,即f(x)=2sin ,因为f=2sin =2sin =2,所以函数f(x)关于直线x=对称,故A错误;
f=2sin =2sin π=0,所以函数f(x)关于对称,故B错误;
对于C:由对于D:由考点三 三角函数的性质及应用
考点三 三角函数的性质及应用——类比对应,寻找“源”头,整体代换
1.三角函数的单调区间
y=sin x的单调递增区间是________________(k∈Z),单调递减区间是________________(k∈Z);
y=cos x的单调递增区间是________________(k∈Z),单调递减区间是________________(k∈Z);
y=tan x的单调递增区间是________________(k∈Z).
[2kπ-,2kπ+]
[2kπ+,2kπ+]
[2kπ-π,2kπ]
[2kπ,2kπ+π]
(kπ-)
2.三角函数的奇偶性与对称性
(1)y=A sin (ωx+φ),当φ=________(k∈Z)时为奇函数;当φ=________(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ+(k∈Z)求得;
(2)y=A cos (ωx+φ),当φ=________(k∈Z)时为奇函数;当φ=________(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ(k∈Z)求得;
(3)y=A tan (ωx+φ),当φ=kπ(k∈Z)时为奇函数.
kπ
kπ+
kπ+
kπ
角度1 单调性为主
例 3 [2022·北京卷]已知函数f(x)=cos2x-sin2x,则( )
A.f(x)在上单调递减
B.f(x)在上单调递增
C.f(x)在上单调递减
D.f(x)在上单调递增
答案:C
解析:f(x)=cos2x-sin2x=cos2x.令2kπ≤2x≤π+2kπ,k∈Z,解得kπ≤x≤+kπ,k∈Z,故f(x)的减区间为[kπ,+kπ],k∈Z.令k=0,则[0,]为f(x)的一个减区间.因为(0,)∈[0,],所以f(x)在(0,)上单调递减.故选C.
归纳总结
判断三角函数单调性的方法技巧
(1)代换法:求形如y=A sin(ωx+φ)(或y=A cos (ωx+φ)(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=z,则y=A sin z(或y=A cos z),然后由复合函数的单调性求得.
(2)图象法:画出三角函数的图象,结合图象求其单调区间.
(3)导数法:利用导数与单调性之间的关系.
角度 2 周期性、奇偶性、对称性为主
例 4 [2022·新疆昌吉测试]已知函数f(x)=sin x-cos x,则下列关于函数y=f的描述错误的是( )
A.奇函数
B.最小正周期为π
C.其图象关于点(-π,0)对称
D.其图象关于直线x=对称
答案:B
解析:因为f(x)=sin x-cos x=2sin ,所以f=2sin x,最小正周期为2π,故B错误;f=2sin x显然为奇函数,其图象关于点(-π,0)对称且关于直线x=对称,所以其它选项均正确.故选B.
归纳总结
1.判断对称中心与对称轴的方法
利用函数y=A sin (ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断.
2.求三角函数周期的常用结论
(1)y=A sin (ωx+φ)和y=A cos (ωx+φ)的最小正周期为,y=tan (ωx+φ)的最小正周期为;
(2)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期,相邻的对称中心与对称轴之间的距离是个周期;正切曲线相邻两对称中心之间的距离是个周期.
对点训练
1.[2021·新高考Ⅰ卷]下列区间中,函数f(x)=7sin 的单调递增区间是( )
A. B.
C. D.
答案:A
解析:因为函数y=sin x的单调递增区间为,
对于函数f=7sin ,由2kπ-解得2kπ-取k=0,可得函数f的一个单调递增区间为,
则 ,A选项满足条件,B不满足条件;
取k=1,可得函数f的一个单调递增区间为 且 ,CD选项均不满足条件.
故选A.
2.[2022·陕西商洛一模]已知直线x=是函数f(x)=sin (0<ω<8)的图象的一条对称轴,则f(x)的最小正周期为( )
A. B.
C.π D.2π
答案:C
解析:因为sin =±1,所以=+kπ,k∈Z,解得ω=6k+2,k∈Z,又0<ω<8,所以ω=2,从而f(x)的最小正周期为T==π.故选C.
3.[2022·内蒙古包头一模]函数f(x)=2sin +2cos 的最小正周期和最大值分别是( )
A.4π和2 B.4π和2
C.8π和2 D.8π和2
答案:C
解析:因为f(x)=2sin +2cos =2sin ,所以函数f(x)的最小正周期为=8π;又sin ∈[-1,1],所以2sin ∈[-2,2],所以函数f(x)的最大值为2.故选C.
考点四 三角函数与其他知识的交汇问题
考点四 三角函数与其他知识的交汇问题 [交汇创新]——画图象,用性质
三角函数的图象与性质是高考考查的重点,近年来,三角函数与其他知识交汇命题成为高考的热点,由原来三角函数与平面向量的交汇渗透到三角函数与函数的零点、数列、不等式、复数、方程等知识的交汇.
例 5 (1)设集合M={y|y=|cos2x-sin2x|,x∈R},N=,则M为( )
A.(0,1) B.(0,1]
C.[0,1) D.[0,1]
答案:C
解析:y=|cos2x-sin2x|=|cos2x|∈[0,1],所以M=[0,1].因为<,所以|x+i|<,即x2+1<2.又因为x∈R,所以-1(2)已知函数f(x)=sin x.若存在x1,x2,…,xm满足0≤x18
解析:因为f(x)=sin x,所以=2,因此要使得满足条件|f(x1)-f(x2)|+|f(x2)-f(x3)|+…+|f(xm-1)-f(xm)|=12的m最小,须取x1=0,x2=,x3=,x4=,x5=,x6=,x7=,x8=6π,即m=8.
归纳总结
解决三角函数与其他知识的交汇问题,要充分利用三角函数的图象与性质.本例(1)是三角函数与复数的交汇,本例(2)是绝对值不等式与三角函数的最值问题,利用放缩法解决.
对点训练
设an=sin ,Sn=a1+a2+…+an,在S1,S2,…,S100中,正数的个数是( )
A.25 B.50
C.75 D.100
答案:D
解析:当1≤n≤24时,an>0,当26≤n≤49时,an<0,但其绝对值要小于1≤n≤24时相应的值;当51≤n≤74时,an>0;当76≤n≤99时,an<0,但其绝对值要小于51≤n≤74时相应的值.故当1≤n≤100时,均有Sn>0.
第1讲 三角函数的图象与性质
考点一
考点二
考点三
考点四
考点一 三角函数的定义、诱导公式及基本关系
考点一 三角函数的定义、诱导公式及基本关系——牢记“口诀”,勿忘“关系”
1.三角函数:设α是一个任意角,它的终边与单位圆交于点P(x,y),则sin α=____,cos α=____,tan α=________.各象限角的三角函数值的符号:一全正,二正弦,三正切,四余弦.
2.同角关系:____________=1,=________.
3.诱导公式:在+α,k∈Z的诱导公式中“奇变偶不变,符号看象限”.
y
x
sin2α+cos2α
tanα
例 1 (1)[2022·湖南长沙一中模拟]若角α的终边过点P(8m,-3),且tan α=,则m的值为( )
A.- B.
C.- D.
答案:A
解析:∵tan α==,∴m=-,故选A.
(2)[2022·安徽蚌埠三模]已知tan α=2,则的值为( )
A.3 B.-3
C. D.-1
答案:A
解析:原式====3.故选A.
归纳总结
利用公式进行化简求值的策略
(1)利用诱导公式化任意角的三角函数为锐角三角函数,其步骤为:去负→脱周→化锐,特别注意函数名称和符号的确定.
(2)利用同角三角函数的关系化简过程要遵循一定的原则,如切化弦、化异为同、化高为低、化繁为简等.
提醒 使用三角函数诱导公式易错的地方有两个:一个是函数名称,一个是函数值的符号.
对点训练
1.[2022·河南新乡二模]已知点A是α的终边与单位圆的交点,若A的横坐标为-,则cos 2α=( )
A. B.-
C. D.-
答案:C
解析:由题意知,cos α=-,所以cos 2α=2cos2α-1=.故选C.
2.[2021·新高考Ⅰ卷]若tan θ=-2,则=( )
A.- B. -
C. D.
答案:C
解析:将式子进行齐次化处理得:
=
=sin θ====.故选C.
考点二
三角函数的图象与解析式
考点二 三角函数的图象与解析式
——平移看“ω,φ”,伸缩看“A,ω”,由图定式找对应,性质、图象结合牢
三角函数图象的变换
先平移后伸缩
先伸缩后平移
例 2 (1)[2022·山东烟台二中检测]若函数f(x)=sin (ωx-φ)的部分图象如图所示,则ω和φ的值是( )
A.ω=1,φ= B.ω=1,φ=-
C.ω=,φ=- D.ω=,φ=
答案:C
解析:由图象可知=,T=4π=,ω=,所以f(x)=sin ,f=sin =1,-φ=2kπ+,φ=-2kπ-(k∈Z),由于|φ|≤,所以φ=-.故选C.
(2)[2022·重庆模拟预测]已知曲线C:y=sin (ωx+φ)的部分图象如图所示,要得到曲线C的图象,可将曲线y=cos x的图象( )
A.先向右平移个单位长度,再将各点的横坐标
缩短到原来的倍,纵坐标不变
B.先向右平移个单位长度,再将各点的横坐标
伸长到原来的2倍,纵坐标不变
C.先向左平移个单位长度,再将各点的横坐标
缩短到原来的倍,纵坐标不变
D.先向左平移个单位长度,再将各点的横坐标伸长到原来的2倍,纵坐标不变
答案:A
解析:因为y=sin (ωx+φ)函数过点,即sin φ=,又|φ|<,所以φ=,即y=sin ,又函数过点,根据五点作图法可知ω+=π,解得ω=2,所以y=sin =sin =cos ,
由y=cos x向右平移个单位长度得到y=cos ,再将y=cos 各点的横坐标缩短到原来的倍,纵坐标不变得到y=cos ,即y=sin .故选A.
归纳总结
由三角函数的图象求解析式y=A sin (ωx+φ)+B(A>0,ω>0)中参数的值.
(1)最值定A,B:根据给定的函数图象确定最值,设最大值为M,最小值为m,则M=A+B,m=-A+B,解得B=,A=.
(2)T定ω:由周期的求解公式T=,可得ω=.
(3)特殊点定φ:代入特殊点求φ,一般代最高点或最低点,代入中心点时应注意是上升趋势还是下降趋势.
提醒 在图象变换过程中务必分清是先相位变换,还是先周期变换.变换只是相对于其中的自变量x而言的,如果x的系数不是1,就要把这个系数提取后再确定变换的单位长度和方向.
对点训练
1.[2021·全国甲卷]已知函数f(x)=2cos (ωx+φ)的部分图象如图所示,则f=________.
-
解析:方法一(五点作图法) 由题图可知T==(T为f(x)的最小正周期),即T=π,所以=π,即ω=2,故f(x)=2cos (2x+φ).点可看作“五点作图法”中的第二个点,故2×+φ=,得φ=-,即f(x)=2cos ,所以f=2cos =-.
方法二(代点法) 由题意知,T==(T为f(x)的最小正周期),所以T=π,=π,即ω=2.又因为点在函数f(x)的图象上,所以2cos =0,所以2×+φ=+kπ(k∈Z),令k=0,则φ=-,所以f(x)=2cos ,所以f=2cos =-2cos =-.
方法三(平移法) 由题意知,T==(T为f(x)的最小正周期),所以T=π,=π,即ω=2.函数y=2cos 2x的图象与x轴的一个交点是,对应函数f(x)=2cos (2x+φ)的图象与x轴的一个交点是,所以f(x)=2cos (2x+φ)的图象是由y=2cos 2x的图象向右平移=个单位长度得到的,所以f(x)=2cos (2x+φ)=2cos 2=2cos ,所以f=2cos =-2cos =-.
2.[2022·四川南充二模]函数f(x)=A sin (2x+θ)的部分图象如图所示,f(0)=,则( )
A.f(x)关于点对称
B.f(x)关于直线x=对称
C.f(x)在上单调递减
D.f(x)在上单调递增
答案:C
解析:由图可知A=2,且f(0)=,所以f(0)=2sin θ=,即sin θ=,因为|θ|≤,所以θ=,即f(x)=2sin ,因为f=2sin =2sin =2,所以函数f(x)关于直线x=对称,故A错误;
f=2sin =2sin π=0,所以函数f(x)关于对称,故B错误;
对于C:由
考点三 三角函数的性质及应用——类比对应,寻找“源”头,整体代换
1.三角函数的单调区间
y=sin x的单调递增区间是________________(k∈Z),单调递减区间是________________(k∈Z);
y=cos x的单调递增区间是________________(k∈Z),单调递减区间是________________(k∈Z);
y=tan x的单调递增区间是________________(k∈Z).
[2kπ-,2kπ+]
[2kπ+,2kπ+]
[2kπ-π,2kπ]
[2kπ,2kπ+π]
(kπ-)
2.三角函数的奇偶性与对称性
(1)y=A sin (ωx+φ),当φ=________(k∈Z)时为奇函数;当φ=________(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ+(k∈Z)求得;
(2)y=A cos (ωx+φ),当φ=________(k∈Z)时为奇函数;当φ=________(k∈Z)时为偶函数;对称轴方程可由ωx+φ=kπ(k∈Z)求得;
(3)y=A tan (ωx+φ),当φ=kπ(k∈Z)时为奇函数.
kπ
kπ+
kπ+
kπ
角度1 单调性为主
例 3 [2022·北京卷]已知函数f(x)=cos2x-sin2x,则( )
A.f(x)在上单调递减
B.f(x)在上单调递增
C.f(x)在上单调递减
D.f(x)在上单调递增
答案:C
解析:f(x)=cos2x-sin2x=cos2x.令2kπ≤2x≤π+2kπ,k∈Z,解得kπ≤x≤+kπ,k∈Z,故f(x)的减区间为[kπ,+kπ],k∈Z.令k=0,则[0,]为f(x)的一个减区间.因为(0,)∈[0,],所以f(x)在(0,)上单调递减.故选C.
归纳总结
判断三角函数单调性的方法技巧
(1)代换法:求形如y=A sin(ωx+φ)(或y=A cos (ωx+φ)(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=z,则y=A sin z(或y=A cos z),然后由复合函数的单调性求得.
(2)图象法:画出三角函数的图象,结合图象求其单调区间.
(3)导数法:利用导数与单调性之间的关系.
角度 2 周期性、奇偶性、对称性为主
例 4 [2022·新疆昌吉测试]已知函数f(x)=sin x-cos x,则下列关于函数y=f的描述错误的是( )
A.奇函数
B.最小正周期为π
C.其图象关于点(-π,0)对称
D.其图象关于直线x=对称
答案:B
解析:因为f(x)=sin x-cos x=2sin ,所以f=2sin x,最小正周期为2π,故B错误;f=2sin x显然为奇函数,其图象关于点(-π,0)对称且关于直线x=对称,所以其它选项均正确.故选B.
归纳总结
1.判断对称中心与对称轴的方法
利用函数y=A sin (ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断.
2.求三角函数周期的常用结论
(1)y=A sin (ωx+φ)和y=A cos (ωx+φ)的最小正周期为,y=tan (ωx+φ)的最小正周期为;
(2)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期,相邻的对称中心与对称轴之间的距离是个周期;正切曲线相邻两对称中心之间的距离是个周期.
对点训练
1.[2021·新高考Ⅰ卷]下列区间中,函数f(x)=7sin 的单调递增区间是( )
A. B.
C. D.
答案:A
解析:因为函数y=sin x的单调递增区间为,
对于函数f=7sin ,由2kπ-
则 ,A选项满足条件,B不满足条件;
取k=1,可得函数f的一个单调递增区间为 且 ,CD选项均不满足条件.
故选A.
2.[2022·陕西商洛一模]已知直线x=是函数f(x)=sin (0<ω<8)的图象的一条对称轴,则f(x)的最小正周期为( )
A. B.
C.π D.2π
答案:C
解析:因为sin =±1,所以=+kπ,k∈Z,解得ω=6k+2,k∈Z,又0<ω<8,所以ω=2,从而f(x)的最小正周期为T==π.故选C.
3.[2022·内蒙古包头一模]函数f(x)=2sin +2cos 的最小正周期和最大值分别是( )
A.4π和2 B.4π和2
C.8π和2 D.8π和2
答案:C
解析:因为f(x)=2sin +2cos =2sin ,所以函数f(x)的最小正周期为=8π;又sin ∈[-1,1],所以2sin ∈[-2,2],所以函数f(x)的最大值为2.故选C.
考点四 三角函数与其他知识的交汇问题
考点四 三角函数与其他知识的交汇问题 [交汇创新]——画图象,用性质
三角函数的图象与性质是高考考查的重点,近年来,三角函数与其他知识交汇命题成为高考的热点,由原来三角函数与平面向量的交汇渗透到三角函数与函数的零点、数列、不等式、复数、方程等知识的交汇.
例 5 (1)设集合M={y|y=|cos2x-sin2x|,x∈R},N=,则M为( )
A.(0,1) B.(0,1]
C.[0,1) D.[0,1]
答案:C
解析:y=|cos2x-sin2x|=|cos2x|∈[0,1],所以M=[0,1].因为<,所以|x+i|<,即x2+1<2.又因为x∈R,所以-1
解析:因为f(x)=sin x,所以=2,因此要使得满足条件|f(x1)-f(x2)|+|f(x2)-f(x3)|+…+|f(xm-1)-f(xm)|=12的m最小,须取x1=0,x2=,x3=,x4=,x5=,x6=,x7=,x8=6π,即m=8.
归纳总结
解决三角函数与其他知识的交汇问题,要充分利用三角函数的图象与性质.本例(1)是三角函数与复数的交汇,本例(2)是绝对值不等式与三角函数的最值问题,利用放缩法解决.
对点训练
设an=sin ,Sn=a1+a2+…+an,在S1,S2,…,S100中,正数的个数是( )
A.25 B.50
C.75 D.100
答案:D
解析:当1≤n≤24时,an>0,当26≤n≤49时,an<0,但其绝对值要小于1≤n≤24时相应的值;当51≤n≤74时,an>0;当76≤n≤99时,an<0,但其绝对值要小于51≤n≤74时相应的值.故当1≤n≤100时,均有Sn>0.
同课章节目录
