(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题一三角函数与解三角形第2讲 三角恒等变换与解三角形 课件(47张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题一三角函数与解三角形第2讲 三角恒等变换与解三角形 课件(47张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 06:03:51 | ||
图片预览











文档简介
(共47张PPT)
第2讲 三角恒等变换与解三角形
考点一
考点二
考点三
考点一 三角恒等变换
——公式要活用,变换要恒等
1.两角和与差的正弦、余弦、正切公式
(1)sin (α±β)=________________;
(2)cos (α±β)=________________;
(3)tan (α±β)=________________.
2.二倍角的正弦、余弦、正切公式
(1)sin 2α=__________;
(2)cos 2α=__________=__________=__________;
(3)tan 2α=__________.
sin αcos β±cos αsin β
cos αcos β sin αsin β
2sin αcos α
cos2α-sin2α
2cos2α-1
1-2sin2α
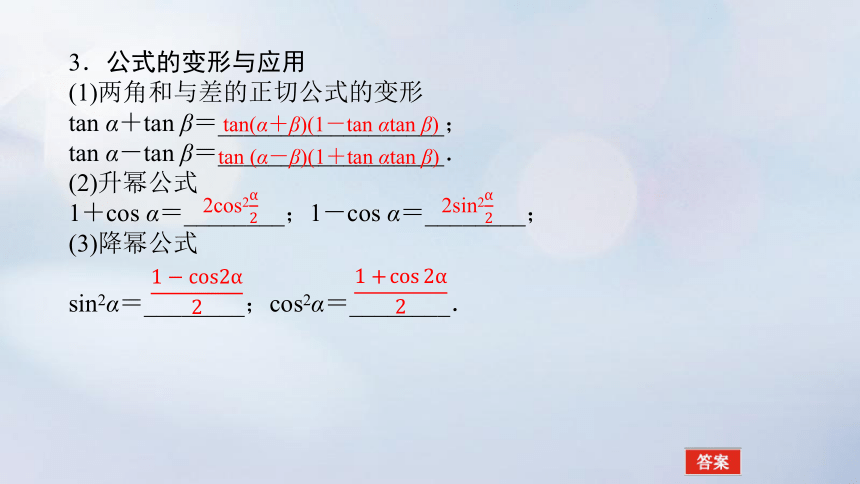
3.公式的变形与应用
(1)两角和与差的正切公式的变形
tan α+tan β=__________________;
tan α-tan β=__________________.
(2)升幂公式
1+cos α=________;1-cos α=________;
(3)降幂公式
sin2α=________;cos2α=________.
tan(α+β)(1-tan αtan β)
tan (α-β)(1+tan αtan β)
2cos2
2sin2
例 1(1)[2022·河北省唐县一中高三练习]已知-tan =2sin θ,则cos θ=( )
A. B.
C. D.
答案:D
解析:因为-tan =2sin θ,所以=2sin θ.所以cos2-sin2=sin2θ,则cosθ=sin2θ>0,即cosθ=1-cos2θ,解得cosθ=(负值舍去).故选D.
(2)已知α∈(0,π),sin α-cos α=,则tan 2α+=( )
A. B.12
C.-12 D.-
答案:C
解析:因为α∈(0,π),sin α-cos α=,sin2α+cos2α=1,解得:sinα=,cos α=,所以tan α=.
所以tan 2α===-.所以tan2α+=-=-12.故选C.
归纳总结
化简三角函数式的规律
规律 解读
一角 一看“角”,这是最重要的一环,通过角之间的差别与联系,把角进行合理地拆分,从而正确使用公式
二名 二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“弦切互化”
三结构 三看“结构特征”,分析结构特征,找到变形的方向,常见的有“遇到分式要通分”“遇根式化被开方式为完全平方式”等
提醒 (1)公式的使用过程要注意正确性,要特别注意公式中的符号和函数名的变换,防止出现“张冠李戴”的情况;
(2)求角问题要注意角的范围,要根据已知条件将所求角的范围尽量缩小,避免产生增解.
对点训练
1.[2021·全国甲卷]若α∈,tan 2α=,则tan α=( )
A. B.
C. D.
答案:A
解析:方法一 因为tan2α==,且tan 2α=,所以=,解得sin α=.因为α∈,所以cos α=,tan α==.故选A.
方法二 因为tan 2α====,且tan2α=,所以=,解得sin α=.因为α∈,所以cos α=,tan α==.故选A.
2.[2022·黑龙江实验中学模拟预测]已知tan =2,则tan =( )
A. B.
C.- D.-
答案:C
解析:∵tan =2,∴tan ==-,
∴tan=tan =tan =-.故选C.
3.[2022·河北省石家庄一模]已知角α∈,tan =,则α=________.
解析:∵tan =,∴=,∴sin =cos ,
∴sin cos α+sin cos =cos sin α-cos sin ,
∴sin cos +cos sin =cos sin α-sin cos α,
∴sin =sin .∵α∈,∴α-∈,∴=α-,则α==.
考点二
利用正、余弦定理解三角形
考点二 利用正、余弦定理解三角形——选用定理,边角互化
1.正弦定理及其变形
在△ABC中,________=________=________=2R(R为△ABC的外接圆半径).变形:a=2R sin A,sin A=,a∶b∶c=sin A∶sin B∶sin C等.
2.余弦定理及其变形
在△ABC中,a2=________________;
变形:b2+c2-a2=2bc cos A,cos A=____________.
3.三角形面积公式
S△ABC=ab sin C=__________=__________.
b2+c2-2bc cos A
bc sin A
ac sin B
角度 1 利用正、余弦定理进行计算
例 2已知△ABC的内角A,B,C的对边分别为a,b,c,且a sin C=c sin .
(1)求角A的大小;
(2)若点D在边BC上,且CD=3BD=3,∠BAD=,求△ABC的面积.
解析:(1)由已知及正弦定理得:sin A sin C=sin C sin ,又B+C=π-A,
∴=,又sin C≠0,
∴sin A=cos ,则2sin cos =cos ,而0<<,
∴cos ≠0,则sin =,故=,得A=.
(2)由∠BAC=,∠BAD=,则∠DAC=.
方法一 在△ABD中,=, ①
在△ADC中,=, ②
∵∠ADB+∠ADC=π,
∴sin ∠BDA=sin ∠ADC, ③
由①②③得:=,又CD=3BD=3,得BD=1,
∴=,不妨设c=2m,b=3m,
在△ABC中,由余弦定理可得,42=(2m)2+(3m)2-2×2m×3m cos ,得m2=,
所以S△ABC=b×c sin ∠BAC=×2m×3m×=.
方法二 ===.
∵△BAD的边BD与△ADC的边DC上的高相等,
∴==,由此得:=,即=,不妨设c=2m,b=3m,
在△ABC中,由余弦定理可得,42=(2m)2+(3m)2-2×2m×3m cos ,得m2=,
所以S△ABC=b×c sin ∠BAC=×2m×3m×=.
归纳总结
1.正、余弦定理的适用条件
(1)“已知两角和一边”或“已知两边和其中一边的对角”应采用正弦定理.
(2)“已知两边和这两边的夹角”或“已知三角形的三边”应采用余弦定理.
2.三角形面积公式的应用原则
(1)对于面积公式S=ab sin C=ac sin B=bc sin A,一般是已知哪一个角就使用含哪个角的公式.
(2)与面积有关的问题,一般要利用正弦定理或余弦定理进行边和角的互化.
角度2 与三角形有关的最值问题
例 3 [2022·陕西西安中学模拟预测]△ABC的内角A,B,C所对的边分别为a,b,c.已知b2+c2-a2=bc,b cos C+c cos B=2,则△ABC的面积的最大值为( )
A.1 B.
C.2 D.2
答案:B
解析:在△ABC中,由余弦定理,b2+c2-a2=bc可化为cos A===.
因为A∈(0,π),所以A=.
由余弦定理,b cos C+c cos B=2可化为:b+c=2,解得:a=2(a=0舍去).
因为b2+c2-a2=bc,所以a2=b2+c2-bc≥2bc-bc=bc,即bc≤4(当且仅当b=c=2时取等号).
所以△ABC的面积S=bc sin A≤×4×=.故选B.
归纳总结
与三角形有关的最值或取值范围问题一般有两类:第一类是求角的最值或取值范围,这时一般应用三角函数值的范围解决;第二类是求边或周长、面积的最值或取值范围,这时一般利用基本不等式或函数的单调性解决.
角度 3 三角形的实际应用
例 4 [2021·全国甲卷] 2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B, C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100;由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为(≈1.732)( )
A.346 B.373
C.446 D.473
答案:B
解析:如图所示,根据题意过C作CE∥C′B′,交BB′于E,过B作BD∥A′B′,交AA′于D,则BE=100,C′B′=CE=.在△A′C′B′中,∠C′A′B′=75°,则BD=A′B′=.又因为在B点处测得A点的仰角为45°,所以AD=BD=,所以高度差AA′-CC′=AD+BE=+100=+100=+100=+100=100(+1)+100≈373.
归纳总结
解三角形应用题的4个要点
提醒 (1)在解决有关高度问题时,理解仰角、俯角、方向(位)角是关键.
(2)在解应用题时,还要根据题意正确画出示意图.
对点训练
1.[2021·宁夏青铜峡市宁朔中学]在△ABC中,a,b,c分别为内角A,B,C所对的边,若a=8,B=60°,C=75°,则b=( )
A.4 B.4 C.4 D.32
答案:C
解析:因为B=60°,C=75°,所以A=180°-60°-75°=45°,因为=,所以b===4.故选C.
2.[2022·河南汝州市第一高级中学模拟]在△ABC中,角A,B,C所对的边分别为a,b,c,a=2,cos 2C=cos 2A+4sin2B,则△ABC面积的最大值是( )
A. B.1 C. D.2
答案:A
解析:由cos 2C=cos 2A+4sin2B得:1-2sin2C=1-2sin2A+4sin2B,
即sin2A=sin2C+2sin2B,由正弦定理得:a2=c2+2b2=4;
由余弦定理得:a2=b2+c2-2bc cosA=4,∴c2+2b2=b2+c2-2bc cos A,即cos A=,∵A∈(0,π),∴sin A= ,
∴S△ABC=bc sin A==,
∵c2+2b2=4,∴c2=4-2b2,
∴S△ABC==,
则当b2=时,max=-+4×=,∴(S△ABC)max==.故选A.
3.[2022·黑龙江哈尔滨三中一模]在△ABC中,内角A,B,C的对边分别是a,b,c,已知c sin-b sin C=0.
(1)求内角B的大小;
(2)已知△ABC的面积为,a=2c,=,求线段BM的长.
解析: (1)因为c sin -b sin C=0,
所以c sin B+c cos B-b sin C=0,
所以由正弦定理边化角得:sin C sin B+sin C cos B-sin B sin C=0,
因为C∈(0,π),sin C≠0,
所以cos B-sin B=0,即tan B=,
因为B∈(0,π),所以B=.
(2)因为△ABC的面积为,B=,
所以S=ac sin B=ac=,
所以ac=2, 因为a=2c,所以c=1,a=2,
所以b== =,
所以a2=b2+c2,即△ABC为直角三角形,
因为=,所以AM=,
所以BM== =.
考点三
与解三角形有关的交汇问题
考点三 与解三角形有关的交汇问题 [交汇创新]——转问题,选定理,得结论
解三角形问题一直是近几年高考的重点,主要考查以斜三角形为背景求三角形的基本量、面积或判断三角形的形状,解三角形与平面向量、不等式、三角函数性质、三角恒等变换交汇命题成为高考的热点.
例 5 如图,在△ABC中,三个内角B,A,C成等差数列,且AC=10,BC=15.
(1)求△ABC的面积;
(2)已知平面直角坐标系xOy中,点D(10,0),若函数f(x)=M sin (ωx+φ)(M>0,ω>0,|φ|<)的图象经过A,C,D三点,且A,D为f(x)的图象与x轴相邻的两个交点,求f(x)的解析式.
解析:(1)在△ABC中,由角B,A,C成等差数列,得B+C=2A,
又因为A+B+C=π,所以A=.
设角A,B,C的对边分别为a,b,c,
由余弦定理可知a2=b2+c2-2bc cos ,
所以c2-10c-125=0,解得c=AB=5+5.
因为CO=10×sin =5,
所以S△ABC=×(5+5)×5=(3).
(2)因为AO=10×cos =5,
所以函数f(x)的最小正周期T=2×(10+5)=30,
故ω=.
因为f(-5)=M sin =0,
所以sin =0,所以-+φ=kπ,k∈Z.
因为|φ|<,所以φ=.
因为f(0)=M sin =5,所以M=10,
所以f(x)=10sin .
归纳总结
解三角形与三角函数交汇问题一般步骤
对点训练
在△ABC中,角A,B,C所对的边分别为a,b,c,a cos B+b cos A=c sin C,数列{an}满足an=(n2+2n)sin [(2n-1)C],则数列{an}的前100项和S100=________.
-5 150
解析:由a cos B+b cos A=c sin C得sin A cos B+sin B cos A=sin2C,
∴sin(A+B)=sin2C,∴sinC=sin2C,
又∵0<C<π,sinC≠0,∴sin C=1,∴C=,
∴an=(n2+2n)sin ,
即an=[(n+1)2-1]sin ,从而S100=(22-1)-(32-1)+(42-1)-(52-1)+…+(1002-1)-(1012-1)=22-32+42-52+…+1002-1012=-(2+3+4+5+…+100+101)=-5 150.
[高考5个大题] 解题研诀窍(一) 三角函数问题重在“变”——变角、变式
[思维流程——找突破口]
[技法指导——迁移搭桥],
1.常用的变角技巧
(1)已知角与特殊角的变换;
(2)已知角与目标角的变换;
(3)角与其倍角的变换;
(4)两角与其和差角的变换以及三角形内角和定理的变换运用.如:α=(α+β)-β=(α-β)+β,2α=(α+β)+(α-β),2α=(β+α)-(β-α),α+β=2·=.
2.常用的变式技巧
主要从函数名、次数、系数方面入手,常见有:
(1)讨论三角函数的性质时,常常将它化为一次的单角的三角函数来讨论;
(2)涉及sin x±cos x、sin x·cos x的问题,常做换元处理,如令t=sin x±cos x∈[-],将原问题转化为关于t的函数来处理;
(3)在解决三角形的问题时,常利用正、余弦定理化边为角或化角为边等.
[典例] 在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b sin A=a cos .
(1)求角B的大小;
(2)设a=2,c=3,求b和sin (2A-B)的值.
[快审题]
求什么 想什么 求角B的大小,想到角B的三角函数值.
求三角函数值,想到由已知三角函数值求值.
给什么 用什么 已知边角关系式,用正弦定理统一角.
已知边的大小,用余弦定理求边.
差什么 找什么 求sin (2A-B)的值,缺少2A的三角函数值,
应找A的三角函数值.
[稳解题]
(1)在△ABC中,由正弦定理=,
可得b sin A=a sin B.
又因为b sin A=a cos ,
所以a sin B=a cos ,
即sin B=cos B+sin B,
所以tan B= .
因为B∈(0,π),所以B=.
(2)在△ABC中,由余弦定理及a=2,c=3,B=,
得b2=a2+c2-2ac cos B=7,故b=.
由b sin A=a cos ,可得sin A=.
因为a所以sin 2A=2sin A cos A=,
cos 2A=2cos2A-1=.
所以sin(2A-B)=sin 2A cos B-cos 2A sin B
==.
题后悟道
1.利用正、余弦定理求解问题的策略
2.三角恒等变换的思路为“一角二名三结构”
升幂(降幂)公式口诀:“幂降一次,角翻倍;幂升一次,角减半”.
第2讲 三角恒等变换与解三角形
考点一
考点二
考点三
考点一 三角恒等变换
——公式要活用,变换要恒等
1.两角和与差的正弦、余弦、正切公式
(1)sin (α±β)=________________;
(2)cos (α±β)=________________;
(3)tan (α±β)=________________.
2.二倍角的正弦、余弦、正切公式
(1)sin 2α=__________;
(2)cos 2α=__________=__________=__________;
(3)tan 2α=__________.
sin αcos β±cos αsin β
cos αcos β sin αsin β
2sin αcos α
cos2α-sin2α
2cos2α-1
1-2sin2α
3.公式的变形与应用
(1)两角和与差的正切公式的变形
tan α+tan β=__________________;
tan α-tan β=__________________.
(2)升幂公式
1+cos α=________;1-cos α=________;
(3)降幂公式
sin2α=________;cos2α=________.
tan(α+β)(1-tan αtan β)
tan (α-β)(1+tan αtan β)
2cos2
2sin2
例 1(1)[2022·河北省唐县一中高三练习]已知-tan =2sin θ,则cos θ=( )
A. B.
C. D.
答案:D
解析:因为-tan =2sin θ,所以=2sin θ.所以cos2-sin2=sin2θ,则cosθ=sin2θ>0,即cosθ=1-cos2θ,解得cosθ=(负值舍去).故选D.
(2)已知α∈(0,π),sin α-cos α=,则tan 2α+=( )
A. B.12
C.-12 D.-
答案:C
解析:因为α∈(0,π),sin α-cos α=,sin2α+cos2α=1,解得:sinα=,cos α=,所以tan α=.
所以tan 2α===-.所以tan2α+=-=-12.故选C.
归纳总结
化简三角函数式的规律
规律 解读
一角 一看“角”,这是最重要的一环,通过角之间的差别与联系,把角进行合理地拆分,从而正确使用公式
二名 二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“弦切互化”
三结构 三看“结构特征”,分析结构特征,找到变形的方向,常见的有“遇到分式要通分”“遇根式化被开方式为完全平方式”等
提醒 (1)公式的使用过程要注意正确性,要特别注意公式中的符号和函数名的变换,防止出现“张冠李戴”的情况;
(2)求角问题要注意角的范围,要根据已知条件将所求角的范围尽量缩小,避免产生增解.
对点训练
1.[2021·全国甲卷]若α∈,tan 2α=,则tan α=( )
A. B.
C. D.
答案:A
解析:方法一 因为tan2α==,且tan 2α=,所以=,解得sin α=.因为α∈,所以cos α=,tan α==.故选A.
方法二 因为tan 2α====,且tan2α=,所以=,解得sin α=.因为α∈,所以cos α=,tan α==.故选A.
2.[2022·黑龙江实验中学模拟预测]已知tan =2,则tan =( )
A. B.
C.- D.-
答案:C
解析:∵tan =2,∴tan ==-,
∴tan=tan =tan =-.故选C.
3.[2022·河北省石家庄一模]已知角α∈,tan =,则α=________.
解析:∵tan =,∴=,∴sin =cos ,
∴sin cos α+sin cos =cos sin α-cos sin ,
∴sin cos +cos sin =cos sin α-sin cos α,
∴sin =sin .∵α∈,∴α-∈,∴=α-,则α==.
考点二
利用正、余弦定理解三角形
考点二 利用正、余弦定理解三角形——选用定理,边角互化
1.正弦定理及其变形
在△ABC中,________=________=________=2R(R为△ABC的外接圆半径).变形:a=2R sin A,sin A=,a∶b∶c=sin A∶sin B∶sin C等.
2.余弦定理及其变形
在△ABC中,a2=________________;
变形:b2+c2-a2=2bc cos A,cos A=____________.
3.三角形面积公式
S△ABC=ab sin C=__________=__________.
b2+c2-2bc cos A
bc sin A
ac sin B
角度 1 利用正、余弦定理进行计算
例 2已知△ABC的内角A,B,C的对边分别为a,b,c,且a sin C=c sin .
(1)求角A的大小;
(2)若点D在边BC上,且CD=3BD=3,∠BAD=,求△ABC的面积.
解析:(1)由已知及正弦定理得:sin A sin C=sin C sin ,又B+C=π-A,
∴=,又sin C≠0,
∴sin A=cos ,则2sin cos =cos ,而0<<,
∴cos ≠0,则sin =,故=,得A=.
(2)由∠BAC=,∠BAD=,则∠DAC=.
方法一 在△ABD中,=, ①
在△ADC中,=, ②
∵∠ADB+∠ADC=π,
∴sin ∠BDA=sin ∠ADC, ③
由①②③得:=,又CD=3BD=3,得BD=1,
∴=,不妨设c=2m,b=3m,
在△ABC中,由余弦定理可得,42=(2m)2+(3m)2-2×2m×3m cos ,得m2=,
所以S△ABC=b×c sin ∠BAC=×2m×3m×=.
方法二 ===.
∵△BAD的边BD与△ADC的边DC上的高相等,
∴==,由此得:=,即=,不妨设c=2m,b=3m,
在△ABC中,由余弦定理可得,42=(2m)2+(3m)2-2×2m×3m cos ,得m2=,
所以S△ABC=b×c sin ∠BAC=×2m×3m×=.
归纳总结
1.正、余弦定理的适用条件
(1)“已知两角和一边”或“已知两边和其中一边的对角”应采用正弦定理.
(2)“已知两边和这两边的夹角”或“已知三角形的三边”应采用余弦定理.
2.三角形面积公式的应用原则
(1)对于面积公式S=ab sin C=ac sin B=bc sin A,一般是已知哪一个角就使用含哪个角的公式.
(2)与面积有关的问题,一般要利用正弦定理或余弦定理进行边和角的互化.
角度2 与三角形有关的最值问题
例 3 [2022·陕西西安中学模拟预测]△ABC的内角A,B,C所对的边分别为a,b,c.已知b2+c2-a2=bc,b cos C+c cos B=2,则△ABC的面积的最大值为( )
A.1 B.
C.2 D.2
答案:B
解析:在△ABC中,由余弦定理,b2+c2-a2=bc可化为cos A===.
因为A∈(0,π),所以A=.
由余弦定理,b cos C+c cos B=2可化为:b+c=2,解得:a=2(a=0舍去).
因为b2+c2-a2=bc,所以a2=b2+c2-bc≥2bc-bc=bc,即bc≤4(当且仅当b=c=2时取等号).
所以△ABC的面积S=bc sin A≤×4×=.故选B.
归纳总结
与三角形有关的最值或取值范围问题一般有两类:第一类是求角的最值或取值范围,这时一般应用三角函数值的范围解决;第二类是求边或周长、面积的最值或取值范围,这时一般利用基本不等式或函数的单调性解决.
角度 3 三角形的实际应用
例 4 [2021·全国甲卷] 2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B, C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100;由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为(≈1.732)( )
A.346 B.373
C.446 D.473
答案:B
解析:如图所示,根据题意过C作CE∥C′B′,交BB′于E,过B作BD∥A′B′,交AA′于D,则BE=100,C′B′=CE=.在△A′C′B′中,∠C′A′B′=75°,则BD=A′B′=.又因为在B点处测得A点的仰角为45°,所以AD=BD=,所以高度差AA′-CC′=AD+BE=+100=+100=+100=+100=100(+1)+100≈373.
归纳总结
解三角形应用题的4个要点
提醒 (1)在解决有关高度问题时,理解仰角、俯角、方向(位)角是关键.
(2)在解应用题时,还要根据题意正确画出示意图.
对点训练
1.[2021·宁夏青铜峡市宁朔中学]在△ABC中,a,b,c分别为内角A,B,C所对的边,若a=8,B=60°,C=75°,则b=( )
A.4 B.4 C.4 D.32
答案:C
解析:因为B=60°,C=75°,所以A=180°-60°-75°=45°,因为=,所以b===4.故选C.
2.[2022·河南汝州市第一高级中学模拟]在△ABC中,角A,B,C所对的边分别为a,b,c,a=2,cos 2C=cos 2A+4sin2B,则△ABC面积的最大值是( )
A. B.1 C. D.2
答案:A
解析:由cos 2C=cos 2A+4sin2B得:1-2sin2C=1-2sin2A+4sin2B,
即sin2A=sin2C+2sin2B,由正弦定理得:a2=c2+2b2=4;
由余弦定理得:a2=b2+c2-2bc cosA=4,∴c2+2b2=b2+c2-2bc cos A,即cos A=,∵A∈(0,π),∴sin A= ,
∴S△ABC=bc sin A==,
∵c2+2b2=4,∴c2=4-2b2,
∴S△ABC==,
则当b2=时,max=-+4×=,∴(S△ABC)max==.故选A.
3.[2022·黑龙江哈尔滨三中一模]在△ABC中,内角A,B,C的对边分别是a,b,c,已知c sin-b sin C=0.
(1)求内角B的大小;
(2)已知△ABC的面积为,a=2c,=,求线段BM的长.
解析: (1)因为c sin -b sin C=0,
所以c sin B+c cos B-b sin C=0,
所以由正弦定理边化角得:sin C sin B+sin C cos B-sin B sin C=0,
因为C∈(0,π),sin C≠0,
所以cos B-sin B=0,即tan B=,
因为B∈(0,π),所以B=.
(2)因为△ABC的面积为,B=,
所以S=ac sin B=ac=,
所以ac=2, 因为a=2c,所以c=1,a=2,
所以b== =,
所以a2=b2+c2,即△ABC为直角三角形,
因为=,所以AM=,
所以BM== =.
考点三
与解三角形有关的交汇问题
考点三 与解三角形有关的交汇问题 [交汇创新]——转问题,选定理,得结论
解三角形问题一直是近几年高考的重点,主要考查以斜三角形为背景求三角形的基本量、面积或判断三角形的形状,解三角形与平面向量、不等式、三角函数性质、三角恒等变换交汇命题成为高考的热点.
例 5 如图,在△ABC中,三个内角B,A,C成等差数列,且AC=10,BC=15.
(1)求△ABC的面积;
(2)已知平面直角坐标系xOy中,点D(10,0),若函数f(x)=M sin (ωx+φ)(M>0,ω>0,|φ|<)的图象经过A,C,D三点,且A,D为f(x)的图象与x轴相邻的两个交点,求f(x)的解析式.
解析:(1)在△ABC中,由角B,A,C成等差数列,得B+C=2A,
又因为A+B+C=π,所以A=.
设角A,B,C的对边分别为a,b,c,
由余弦定理可知a2=b2+c2-2bc cos ,
所以c2-10c-125=0,解得c=AB=5+5.
因为CO=10×sin =5,
所以S△ABC=×(5+5)×5=(3).
(2)因为AO=10×cos =5,
所以函数f(x)的最小正周期T=2×(10+5)=30,
故ω=.
因为f(-5)=M sin =0,
所以sin =0,所以-+φ=kπ,k∈Z.
因为|φ|<,所以φ=.
因为f(0)=M sin =5,所以M=10,
所以f(x)=10sin .
归纳总结
解三角形与三角函数交汇问题一般步骤
对点训练
在△ABC中,角A,B,C所对的边分别为a,b,c,a cos B+b cos A=c sin C,数列{an}满足an=(n2+2n)sin [(2n-1)C],则数列{an}的前100项和S100=________.
-5 150
解析:由a cos B+b cos A=c sin C得sin A cos B+sin B cos A=sin2C,
∴sin(A+B)=sin2C,∴sinC=sin2C,
又∵0<C<π,sinC≠0,∴sin C=1,∴C=,
∴an=(n2+2n)sin ,
即an=[(n+1)2-1]sin ,从而S100=(22-1)-(32-1)+(42-1)-(52-1)+…+(1002-1)-(1012-1)=22-32+42-52+…+1002-1012=-(2+3+4+5+…+100+101)=-5 150.
[高考5个大题] 解题研诀窍(一) 三角函数问题重在“变”——变角、变式
[思维流程——找突破口]
[技法指导——迁移搭桥],
1.常用的变角技巧
(1)已知角与特殊角的变换;
(2)已知角与目标角的变换;
(3)角与其倍角的变换;
(4)两角与其和差角的变换以及三角形内角和定理的变换运用.如:α=(α+β)-β=(α-β)+β,2α=(α+β)+(α-β),2α=(β+α)-(β-α),α+β=2·=.
2.常用的变式技巧
主要从函数名、次数、系数方面入手,常见有:
(1)讨论三角函数的性质时,常常将它化为一次的单角的三角函数来讨论;
(2)涉及sin x±cos x、sin x·cos x的问题,常做换元处理,如令t=sin x±cos x∈[-],将原问题转化为关于t的函数来处理;
(3)在解决三角形的问题时,常利用正、余弦定理化边为角或化角为边等.
[典例] 在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b sin A=a cos .
(1)求角B的大小;
(2)设a=2,c=3,求b和sin (2A-B)的值.
[快审题]
求什么 想什么 求角B的大小,想到角B的三角函数值.
求三角函数值,想到由已知三角函数值求值.
给什么 用什么 已知边角关系式,用正弦定理统一角.
已知边的大小,用余弦定理求边.
差什么 找什么 求sin (2A-B)的值,缺少2A的三角函数值,
应找A的三角函数值.
[稳解题]
(1)在△ABC中,由正弦定理=,
可得b sin A=a sin B.
又因为b sin A=a cos ,
所以a sin B=a cos ,
即sin B=cos B+sin B,
所以tan B= .
因为B∈(0,π),所以B=.
(2)在△ABC中,由余弦定理及a=2,c=3,B=,
得b2=a2+c2-2ac cos B=7,故b=.
由b sin A=a cos ,可得sin A=.
因为a
cos 2A=2cos2A-1=.
所以sin(2A-B)=sin 2A cos B-cos 2A sin B
==.
题后悟道
1.利用正、余弦定理求解问题的策略
2.三角恒等变换的思路为“一角二名三结构”
升幂(降幂)公式口诀:“幂降一次,角翻倍;幂升一次,角减半”.
同课章节目录
