北师大版七年级数学下册3.2用关系式表示变量关系导学案(含简单答案)
文档属性
| 名称 | 北师大版七年级数学下册3.2用关系式表示变量关系导学案(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 578.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 19:02:05 | ||
图片预览

文档简介
3.2 用关系式表示变量关系
导学案
学习目标
1.经历探索某些图形中变量之间的关系的过程,进一步体验一个变量的变化对另一个变量的影响,发展符号感.
2.能根据具体情况,用关系式表示某些变量之间的关系.
3.能根据关系式求值,初步体会自变量和因变量的数值对应关系.
重点
1.列关系式表示两个变量的关系.
2.根据图形的面积公式或体积公式来求两个变量之间的关系式,会利用关系式根据任何一个自变量的值,求出相应因变量的值.
难点
将具体问题抽象成数学问题并将它用关系式表示出来.
一、自学释疑
用图表表示变量关系应该注意什么?如何用关系式表示变量关系?
二、合作探究
探究点一、变化中的三角形
看图回答下列问题:
图中的三角形ABC底边BC上的高是6厘米,当三角形的顶点C沿着底边所在直线向B点运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变量分别是什么?
(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为________.
(3)当底边长从12厘米变化到3厘米时,三角形的面积从________厘米2变化到________厘米2.
探究点二、变化中的圆锥
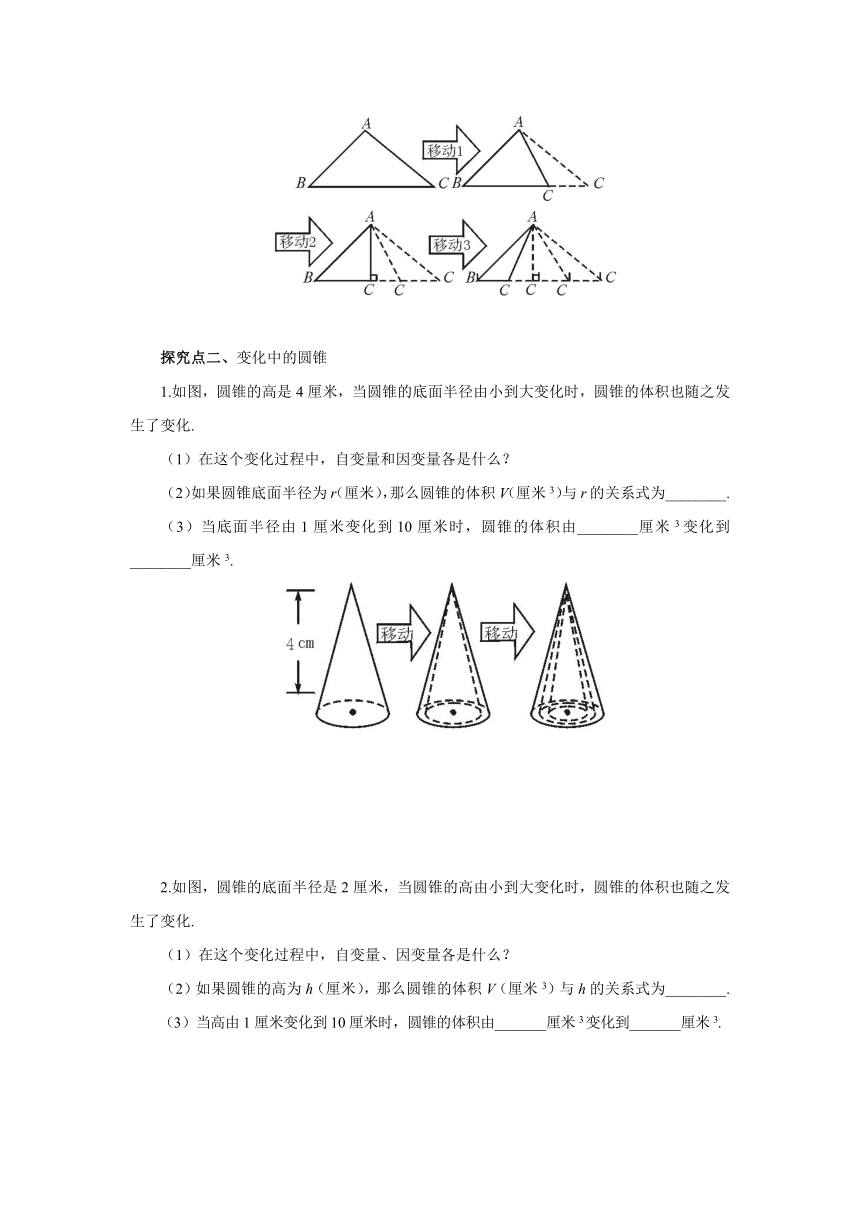
1.如图,圆锥的高是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)如果圆锥底面半径为r(厘米),那么圆锥的体积V(厘米3)与r的关系式为________.
(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由________厘米3变化到________厘米3.
2.如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥的高为h(厘米),那么圆锥的体积V(厘米3)与h的关系式为________.
(3)当高由1厘米变化到10厘米时,圆锥的体积由_______厘米3变化到_______厘米3.
三、随堂检测
1.有一本书,每20页厚1 mm,设从第1页到第x页的厚度为y mm,则( )
A.y=x B.y=20x
C.y=+x D.y=
2.某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了.如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的关系式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60-0.12x,x>0 C.y=0.12x,0≤x≤500 D.y=60-0.12x,0≤x≤500
3.如图,梯形的上底长是5 cm,下底长是11 cm.当梯形的高由大变小时,梯形的面积也随之发生变化.
(1)在这个变化过程中,自变量是____________,因变量是____________;
(2)梯形的面积y(cm2)与高x(cm)之间的关系式为____________;
(3)当梯形的高由10 cm变化到1 cm时,梯形的面积由____________变化到____________.
4.有一种粗细均匀的电线,为了确定其长度,从一捆上剪下1 m,称得它的质量是0.06 kg.
(1)写出这种电线长度与质量之间的关系式;
(2)如果一捆电线剪下1 m后的质量为b kg,请写出这捆电线的总长度.
我的收获
__________________________________________________________________________________________________________________________________________
参考答案
随堂检测
1.A
2.D
3. (1)梯形的高;梯形的面积 (2)y=8x (3)80 cm2;8 cm2
4.解:(1)设电线的长度为l m,质量为m kg,则有l=.
(2)设这捆电线的总长度为L m,则L=+1,即这捆电线的总长度为 m.
导学案
学习目标
1.经历探索某些图形中变量之间的关系的过程,进一步体验一个变量的变化对另一个变量的影响,发展符号感.
2.能根据具体情况,用关系式表示某些变量之间的关系.
3.能根据关系式求值,初步体会自变量和因变量的数值对应关系.
重点
1.列关系式表示两个变量的关系.
2.根据图形的面积公式或体积公式来求两个变量之间的关系式,会利用关系式根据任何一个自变量的值,求出相应因变量的值.
难点
将具体问题抽象成数学问题并将它用关系式表示出来.
一、自学释疑
用图表表示变量关系应该注意什么?如何用关系式表示变量关系?
二、合作探究
探究点一、变化中的三角形
看图回答下列问题:
图中的三角形ABC底边BC上的高是6厘米,当三角形的顶点C沿着底边所在直线向B点运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变量分别是什么?
(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为________.
(3)当底边长从12厘米变化到3厘米时,三角形的面积从________厘米2变化到________厘米2.
探究点二、变化中的圆锥
1.如图,圆锥的高是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)如果圆锥底面半径为r(厘米),那么圆锥的体积V(厘米3)与r的关系式为________.
(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由________厘米3变化到________厘米3.
2.如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥的高为h(厘米),那么圆锥的体积V(厘米3)与h的关系式为________.
(3)当高由1厘米变化到10厘米时,圆锥的体积由_______厘米3变化到_______厘米3.
三、随堂检测
1.有一本书,每20页厚1 mm,设从第1页到第x页的厚度为y mm,则( )
A.y=x B.y=20x
C.y=+x D.y=
2.某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了.如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的关系式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60-0.12x,x>0 C.y=0.12x,0≤x≤500 D.y=60-0.12x,0≤x≤500
3.如图,梯形的上底长是5 cm,下底长是11 cm.当梯形的高由大变小时,梯形的面积也随之发生变化.
(1)在这个变化过程中,自变量是____________,因变量是____________;
(2)梯形的面积y(cm2)与高x(cm)之间的关系式为____________;
(3)当梯形的高由10 cm变化到1 cm时,梯形的面积由____________变化到____________.
4.有一种粗细均匀的电线,为了确定其长度,从一捆上剪下1 m,称得它的质量是0.06 kg.
(1)写出这种电线长度与质量之间的关系式;
(2)如果一捆电线剪下1 m后的质量为b kg,请写出这捆电线的总长度.
我的收获
__________________________________________________________________________________________________________________________________________
参考答案
随堂检测
1.A
2.D
3. (1)梯形的高;梯形的面积 (2)y=8x (3)80 cm2;8 cm2
4.解:(1)设电线的长度为l m,质量为m kg,则有l=.
(2)设这捆电线的总长度为L m,则L=+1,即这捆电线的总长度为 m.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
