2.4 单摆 同步练习(学生版+解析版)
文档属性
| 名称 | 2.4 单摆 同步练习(学生版+解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-20 13:15:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.4 单摆 同步练习
一、单选题
1.关于单摆的运动,下列说法正确的是( )
①单摆的回复力是摆线的拉力与重力的合力
②单摆的回复力是重力沿摆球运动轨迹切向的分力
③单摆的周期与摆球质量无关,与振幅无关,与摆长和当地的重力加速度有关
④单摆的运动是简谐运动
⑤在山脚下走时准确的摆钟移到高山上走时将变快
A.③④ B.②③
C.③④⑤ D.①④⑤
2.在盛沙的漏斗下面放一木板,让漏斗左右摆动起来,同时其中细沙匀速流出,经历一段时间后,观察木板上沙子的堆积情况,则沙堆的剖面应是下图中的( )
A. B.
C. D.
3.有一摆长为L的单摆,其悬点正下方某处有一小钉,摆球经过平衡位置向左摆动时,摆线的上部被小钉挡住,使摆长发生变化。现使摆球做小幅度摆动,摆球从右边最高点M运动到左边最高点N的频闪照片如图所示(悬点与小钉未被摄入)。P为摆动中的最低点,已知每相邻两次闪光的时间间隔相等,由此可知,小钉与悬点间的距离为( )
A. B. C. D.无法确定
4.如图甲所示,一单摆悬挂在拉力传感器上。让单摆在竖直面内做小角度摆动,拉力传感器显示绳子拉力的大小随时间的变化图像如图乙所示,已知当地的重力加速度为,则根据图乙中的数据可知( )
A.此单摆的周期
B.此摆球的质量为
C.此单摆的摆长
D.在时刻摆球的回复力最小
5.如图所示,摆长为L的单摆,周期为T.如果在悬点O的正下方的B点固定一个光滑的钉子,OB的距离为OA长度的5/9,使摆球A通过最低点向左摆动,悬线被钉子挡住成为一个新的单摆,则下列说法中正确的是 ( )
A.单摆在整个振动过程中的周期不变
B.单摆在整个振动过程中的周期将变大为原来的6/5倍
C.单摆在整个振动过程中的周期将变小为原来的5/6倍
D.单摆在整个振动过程中的周期无法确定
6.某单摆在竖直平面内做小摆角振动,周期为2 s。如果从摆球向右运动通过平衡位置时开始计时,在t=1.4 s至t=1.5 s的过程中,摆球的( )
A.速度向右在增大,加速度向右在减小
B.速度向左在增大,加速度向左在增大
C.速度向左在减小,加速度向右在增大
D.速度向右在减小,加速度向左在减小
7.如图所示,在两根等长的曲线下悬挂一个小球(可视为质点)组成了所谓的双线摆,若摆长为l,两线与天花板的左、右两侧夹角均为α,当小球垂直纸面做简谐运动时,其周期为( )
A.2π B.2π
C.2π D.2π
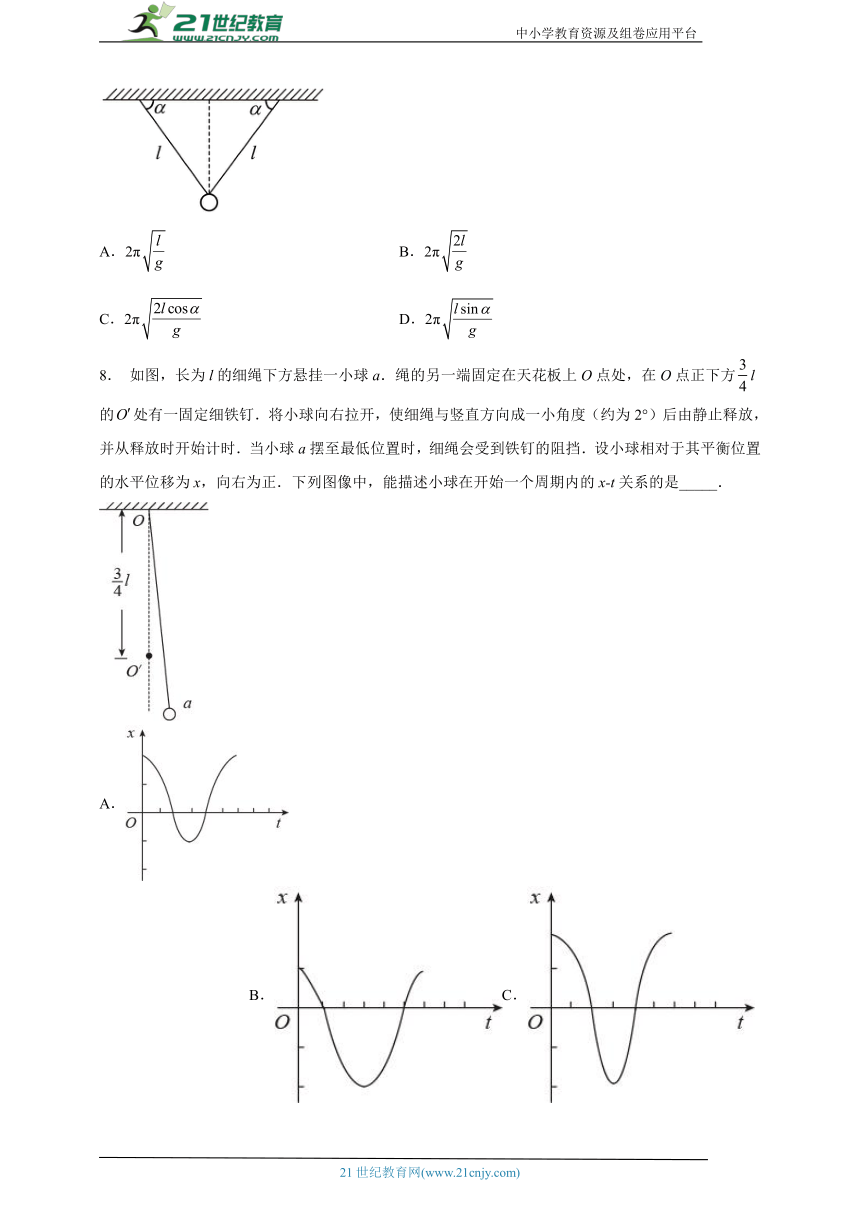
8. 如图,长为l的细绳下方悬挂一小球a.绳的另一端固定在天花板上O点处,在O点正下方l的处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图像中,能描述小球在开始一个周期内的x-t关系的是_____.
A. B.C. D.
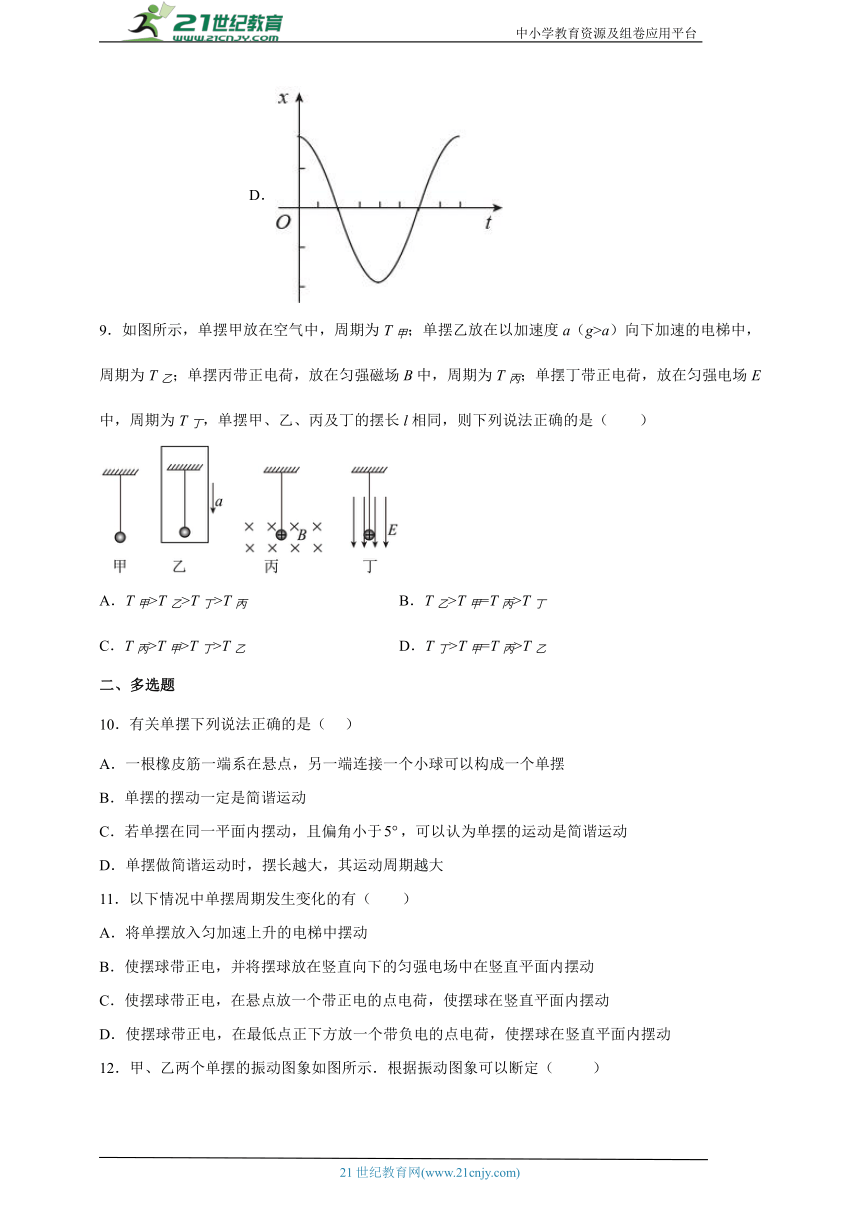
9.如图所示,单摆甲放在空气中,周期为T甲;单摆乙放在以加速度a(g>a)向下加速的电梯中,周期为T乙;单摆丙带正电荷,放在匀强磁场B中,周期为T丙;单摆丁带正电荷,放在匀强电场E中,周期为T丁,单摆甲、乙、丙及丁的摆长l相同,则下列说法正确的是( )
A.T甲>T乙>T丁>T丙 B.T乙>T甲=T丙>T丁
C.T丙>T甲>T丁>T乙 D.T丁>T甲=T丙>T乙
二、多选题
10.有关单摆下列说法正确的是( )
A.一根橡皮筋一端系在悬点,另一端连接一个小球可以构成一个单摆
B.单摆的摆动一定是简谐运动
C.若单摆在同一平面内摆动,且偏角小于,可以认为单摆的运动是简谐运动
D.单摆做简谐运动时,摆长越大,其运动周期越大
11.以下情况中单摆周期发生变化的有( )
A.将单摆放入匀加速上升的电梯中摆动
B.使摆球带正电,并将摆球放在竖直向下的匀强电场中在竖直平面内摆动
C.使摆球带正电,在悬点放一个带正电的点电荷,使摆球在竖直平面内摆动
D.使摆球带正电,在最低点正下方放一个带负电的点电荷,使摆球在竖直平面内摆动
12.甲、乙两个单摆的振动图象如图所示.根据振动图象可以断定( )
A.若甲、乙两单摆在同一地点摆动,甲、乙两单摆摆长之比是9:4
B.甲、乙两单摆振动的频率之比是3:2
C.甲、乙两单摆振动的周期之比是2:3
D.若甲、乙两单摆在不同一地点摆动,但摆长相同,则甲乙两单摆所在地点的重力加速度之比为9:4
13.惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟。摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制。旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动,如图所示,以下说法正确的是( )
A.当摆钟不准确时需要调整圆盘的位置
B.摆钟快了应使圆盘沿摆杆上移
C.由冬季变为夏季时应使圆盘沿摆杆上移
D.把摆钟从福建移到北京应使 圆盘沿摆杆上移
14.如图所示,长度为l的轻绳上端固定在O点,下端系一小球(小球可以看成质点)。在O点正下方,距O点处的P点固定一颗小钉子。现将小球拉到点A处,轻绳被拉直,然后由静止释放小球。点B是小球运动的最低位置,点C(图中未标出)是小球能够到达的左方最高位置。已知点A与点B之间的高度差为h,h<A.点C与点B高度差小于h
B.点C与点B高度差等于h
C.小球摆动的周期等于
D.小球摆动的周期等于
15.甲、乙两位同学分别使用图甲中所示的装置,观察单摆做简谐运动时的振动图像。已知两人实验时所用的摆长相同,落在同一木板上的细砂形成的曲线分别如图乙中、所示。下列关于两图线的分析,正确的是( )
A.对应的细砂摆摆动的幅度较大,对应的细砂摆摆动的幅度较小
B.与对应的细砂摆周期相同
C.对应的木板运动速度比对应的木板运动速度大
D.假设两次实验细砂摆质量相等,则对应的细砂摆摆到最低点时,摆线的拉力比对应的拉力大
16.将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动。用频闪照相机拍到如图所示的单摆从左到右单程过程的频闪照片,以下说法中正确的是( )
A.摆线碰到障碍物前后的摆长之比为9︰4
B.摆线碰到障碍物前后的摆长之比为3︰2
C.摆线经过最低点时,线速度不变,半径减小
D.摆线经过最低点时,角速度变大,半径不变
三、解答题
17.如图所示,光滑的半球壳半径为R,O点在球心O′的正下方,一小球甲(可视为质点)由距O点很近的A点由静止释放,R 。
(1)若小球甲释放的同时,另一小球乙(可视为质点)从球心O′处自由落下,求两球第一次到达O点的时间比;
(2)若小球甲释放的同时,另一小球丙(可视为质点)在O点正上方某处自由落下,为使两球在O点相碰,小球应由多高处自由落下?
18.如图所示为理想单摆,摆角足够小,可认为是简谐运动,其平衡位置记为O点。
(1)若已知摆球的质量为m,摆长为L,在摆角很小时,摆球对于O点的位移x的大小与角对应的弧长近似相等,即近似满足。请推导得出摆球在任意位置处的回复力与位移的比例常数k的表达式。
(2)若仅知道单摆的振幅A及摆球所受回复力与位移的比例常数k,求摆球在振动位移为时的动能(用A和k表示)。
19.将一测力传感器连接到计算机上就可以测量快速变化的力,如图(a)所示点O为单摆的悬点,将传感器接在摆线与点O之间,现将小球(可视为质点)拉到点A,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中点B为运动最低位置,,小于5°且是未知量。如图(b)所示是由计算得到细线对摆球的拉力大小F随时间变化的图像,且图中时刻为摆球从点A开始运动的时刻,据力学规律和题中信息(g取),求:
(1)单摆的周期和摆长;
(2)摆球的质量及摆动过程中的最大速度。
2.4 单 摆
一、单选题
1.关于单摆的运动,下列说法正确的是( )
①单摆的回复力是摆线的拉力与重力的合力
②单摆的回复力是重力沿摆球运动轨迹切向的分力
③单摆的周期与摆球质量无关,与振幅无关,与摆长和当地的重力加速度有关
④单摆的运动是简谐运动
⑤在山脚下走时准确的摆钟移到高山上走时将变快
A.③④ B.②③
C.③④⑤ D.①④⑤
【答案】B
【解析】①②.单摆的回复力是重力沿摆球运动轨迹切向的分力,选项①错误,②正确;
③.根据可知,单摆的周期与摆球质量无关,与振幅无关,与摆长和当地的重力加速度有关,则③正确;
④.单摆在同一平面内摆动,只有当偏角小于5°时,可以认为单摆的运动是简谐运动,则④错误;
⑤.根据,在山脚下走时准确的摆钟移到高山上时,由于重力加速度g变小,则周期变大,则摆钟走时将变慢,⑤错误。故选B。
2.在盛沙的漏斗下面放一木板,让漏斗左右摆动起来,同时其中细沙匀速流出,经历一段时间后,观察木板上沙子的堆积情况,则沙堆的剖面应是下图中的( )
A. B.
C. D.
【答案】B
【解析】不考虑空气阻力,漏斗在从最左端向最右端运动和从最右端向最左端运动时,到达最底端运动速度最快,细沙漏到地面上的最少,两端漏斗运动的最慢,细沙漏到地面上的最多,故选项B正确,选项A、C、D错误;
故选选项B.
3.有一摆长为L的单摆,其悬点正下方某处有一小钉,摆球经过平衡位置向左摆动时,摆线的上部被小钉挡住,使摆长发生变化。现使摆球做小幅度摆动,摆球从右边最高点M运动到左边最高点N的频闪照片如图所示(悬点与小钉未被摄入)。P为摆动中的最低点,已知每相邻两次闪光的时间间隔相等,由此可知,小钉与悬点间的距离为( )
A. B. C. D.无法确定
【答案】C
【解析】设每相邻两次闪光的时间间隔为t,则摆长为L时单摆摆动的周期为
摆长为'时单摆摆动的周期为
所以
T1∶T2=2∶1
又因为
故可得
所以小钉与悬点间的距离为
故选C。
4.如图甲所示,一单摆悬挂在拉力传感器上。让单摆在竖直面内做小角度摆动,拉力传感器显示绳子拉力的大小随时间的变化图像如图乙所示,已知当地的重力加速度为,则根据图乙中的数据可知( )
A.此单摆的周期
B.此摆球的质量为
C.此单摆的摆长
D.在时刻摆球的回复力最小
【答案】C
【解析】A.摆球运动到最低点时,由重力和绳子拉力的合力提供向心力,所以摆球运动到最低点时,绳子拉力最大,则此单摆的周期为
故A错误;
B.摆球运动到最低点时,由重力和绳子拉力的合力提供向心力,则有
此摆球的质量为
故B错误;
C.根据单摆周期公式
可得此单摆的摆长
故C正确;
D.单摆的回复力是重力沿摆球运动轨迹切向的分力提供,摆球运动到最低点时,摆球的回复力最小,所以在时刻摆球的回复力最小,在时刻摆球的回复力最大,故D错误。故选C。
5.如图所示,摆长为L的单摆,周期为T.如果在悬点O的正下方的B点固定一个光滑的钉子,OB的距离为OA长度的5/9,使摆球A通过最低点向左摆动,悬线被钉子挡住成为一个新的单摆,则下列说法中正确的是 ( )
A.单摆在整个振动过程中的周期不变
B.单摆在整个振动过程中的周期将变大为原来的6/5倍
C.单摆在整个振动过程中的周期将变小为原来的5/6倍
D.单摆在整个振动过程中的周期无法确定
【答案】C
【解析】根据单摆周期公式:,未加钉子时,周期:,悬线长变为被挡后,周期变为,所以加了钉子的周期为:,所以周期变为原来的,ABD错误C正确
6.某单摆在竖直平面内做小摆角振动,周期为2 s。如果从摆球向右运动通过平衡位置时开始计时,在t=1.4 s至t=1.5 s的过程中,摆球的( )
A.速度向右在增大,加速度向右在减小
B.速度向左在增大,加速度向左在增大
C.速度向左在减小,加速度向右在增大
D.速度向右在减小,加速度向左在减小
【答案】C
【解析】单摆的周期为2 s,摆球向右通过平衡位置时开始计时,当t=1.4 s时,摆球已通过平衡位置,正在向左方最大位移处做减速运动,由于位移在变大,根据
可知,加速度也在变大,方向向右,C正确。故选C。
7.如图所示,在两根等长的曲线下悬挂一个小球(可视为质点)组成了所谓的双线摆,若摆长为l,两线与天花板的左、右两侧夹角均为α,当小球垂直纸面做简谐运动时,其周期为( )
A.2π B.2π
C.2π D.2π
【答案】D
【解析】根据公式:
T=2π
本题中:
l′=lsin α
所以有:
T=2π.
ABC.由上计算得T为2π,ABC错误;
D. 由上计算得T为2π,D正确
8. 如图,长为l的细绳下方悬挂一小球a.绳的另一端固定在天花板上O点处,在O点正下方l的处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图像中,能描述小球在开始一个周期内的x-t关系的是_____.
A. B.C. D.
【答案】A
【解析】由T=2π得:T1=2π,T2=2π=π=T1 ,故BD错误;
,
由能量守恒定律可知,小球先后摆起得最大高度相同,故l-lcosθ1=
根据数学规律可得: 故,即第一次振幅是第二次振幅得2倍,故A正确,C错误.
9.如图所示,单摆甲放在空气中,周期为T甲;单摆乙放在以加速度a(g>a)向下加速的电梯中,周期为T乙;单摆丙带正电荷,放在匀强磁场B中,周期为T丙;单摆丁带正电荷,放在匀强电场E中,周期为T丁,单摆甲、乙、丙及丁的摆长l相同,则下列说法正确的是( )
A.T甲>T乙>T丁>T丙 B.T乙>T甲=T丙>T丁
C.T丙>T甲>T丁>T乙 D.T丁>T甲=T丙>T乙
【答案】B
【解析】根据单摆公式,对甲摆有
T甲=2π
对乙摆有
T乙=2π
对丙摆,由于摆动过程中洛伦兹力总是垂直于速度方向,故不可能产生沿圆弧切向的分力效果而参与提供回复力,所以周期不变,即
T丙=2π
对丁摆,由于摆球受竖直向下的重力的同时,还受竖直向下的电场力,电场力在圆弧切向产生分力,与重力沿切向的分力一起提供回复力,相当于重力增大了。等效重力
F=mg+qE
故等效重力加速度
故周期
T丁=2π
所以
T乙>T甲=T丙>T丁
ACD错误,B正确。故选B。
二、多选题
10.有关单摆下列说法正确的是( )
A.一根橡皮筋一端系在悬点,另一端连接一个小球可以构成一个单摆
B.单摆的摆动一定是简谐运动
C.若单摆在同一平面内摆动,且偏角小于,可以认为单摆的运动是简谐运动
D.单摆做简谐运动时,摆长越大,其运动周期越大
【答案】CD
【解析】A.一根不可伸长的细绳一端系在悬点,另一端连接一个质量较大体积较小的小球可以构成一个单摆,A错误;
BC.若单摆在同一平面内摆动,且偏角小于5°,可以认为单摆的运动是简谐运动,B错误,C正确;
D.根据可知,单摆做简谐运动时,摆长越大,其运动周期越大,D正确。
故选CD。
11.以下情况中单摆周期发生变化的有( )
A.将单摆放入匀加速上升的电梯中摆动
B.使摆球带正电,并将摆球放在竖直向下的匀强电场中在竖直平面内摆动
C.使摆球带正电,在悬点放一个带正电的点电荷,使摆球在竖直平面内摆动
D.使摆球带正电,在最低点正下方放一个带负电的点电荷,使摆球在竖直平面内摆动
【答案】AB
【解析】A.由
可知,将单摆放入匀加速上升的电梯中,单摆处于超重状态,等效重力加速度变大,周期将减小,故A正确;
B.使摆球带正电,将摆球放在竖直向下的匀强电场中在竖直平面内摆动,摆球受到竖直向下的电场力和重力作用,等效重力加速度变大,周期将减小,故B正确;
CD.在悬点放一个带正电的点电荷,或在最低点正下方放一个带负电的点电荷,使摆球在竖直平面内摆动,正点电荷或负点电荷在一个周期内对摆球做的功均为0,周期将不变,故C、D错误。
故选AB。
12.甲、乙两个单摆的振动图象如图所示.根据振动图象可以断定( )
A.若甲、乙两单摆在同一地点摆动,甲、乙两单摆摆长之比是9:4
B.甲、乙两单摆振动的频率之比是3:2
C.甲、乙两单摆振动的周期之比是2:3
D.若甲、乙两单摆在不同一地点摆动,但摆长相同,则甲乙两单摆所在地点的重力加速度之比为9:4
【答案】BCD
【解析】ABC.根据图像可知,单摆振动的周期关系
所以周期之比为
频率为周期的反比,所以频率之比
若甲乙在同一地点,则重力加速度相同,根据周期公式
所以摆长之比为4:9,A错误BC正确;
D.若在不同地点,摆长相同,根据
得重力加速度之比为9:4,D正确。故选BCD。
13.惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟。摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制。旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动,如图所示,以下说法正确的是( )
A.当摆钟不准确时需要调整圆盘的位置
B.摆钟快了应使圆盘沿摆杆上移
C.由冬季变为夏季时应使圆盘沿摆杆上移
D.把摆钟从福建移到北京应使 圆盘沿摆杆上移
【答案】AC
【解析】A.根据周期公式,当摆钟不准确时,则需要调整摆长,A正确;
B.摆钟快了,周期小,则需将摆长增加,增大周期,B错误;
C.由冬季变为夏季时摆杆受热伸长,则需上移调节,C正确;
D.摆钟从福建移到北京,加速度增大,则需将摆长增加,D错误。
故选AC。
14.如图所示,长度为l的轻绳上端固定在O点,下端系一小球(小球可以看成质点)。在O点正下方,距O点处的P点固定一颗小钉子。现将小球拉到点A处,轻绳被拉直,然后由静止释放小球。点B是小球运动的最低位置,点C(图中未标出)是小球能够到达的左方最高位置。已知点A与点B之间的高度差为h,h<A.点C与点B高度差小于h
B.点C与点B高度差等于h
C.小球摆动的周期等于
D.小球摆动的周期等于
【答案】BC
【解析】AB.小球摆动过程中,只有重力做功,机械能守恒,两侧最高点动能均为零,故重力势能也相等,故最大高度相同,故A错误,B正确;
CD.小球B→A→B的时间为
小球B→C→B的时间为
故小球摆动的周期为
故C正确,D错误。故选BC。
15.甲、乙两位同学分别使用图甲中所示的装置,观察单摆做简谐运动时的振动图像。已知两人实验时所用的摆长相同,落在同一木板上的细砂形成的曲线分别如图乙中、所示。下列关于两图线的分析,正确的是( )
A.对应的细砂摆摆动的幅度较大,对应的细砂摆摆动的幅度较小
B.与对应的细砂摆周期相同
C.对应的木板运动速度比对应的木板运动速度大
D.假设两次实验细砂摆质量相等,则对应的细砂摆摆到最低点时,摆线的拉力比对应的拉力大
【答案】BC
【解析】A.由题图乙可知,对应的细砂摆摆动的幅度与对应的细砂摆摆动的幅度相同,故A错误;
B.由单摆周期公式
及两摆摆长相同可知,周期相同,故B正确;
C.由题图乙可知,若对应的木板的运动时间为,则对应的木板的运动时间为,可知对应的木板运动速度比对应的木板运动速度大,故C正确;
D.由动能定理有
在最低点有
解得
由于两摆的振动幅度相同,则相同,故拉力相同,故D错误。
故选BC。
16.将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动。用频闪照相机拍到如图所示的单摆从左到右单程过程的频闪照片,以下说法中正确的是( )
A.摆线碰到障碍物前后的摆长之比为9︰4
B.摆线碰到障碍物前后的摆长之比为3︰2
C.摆线经过最低点时,线速度不变,半径减小
D.摆线经过最低点时,角速度变大,半径不变
【答案】AC
【解析】AB.频闪照片拍摄的时间间隔一定,由图可知,摆线与障碍物碰撞前后的周期之比为3:2,根据单摆的周期公式得,摆长之比为9:4,故A正确,B错误;
CD.摆线碰到障碍物的瞬间,摆球的速度不能发生突变,即线速度不变。根据v=rω可知,摆球转动的半径减小,线速度不变,所以角速度增大,故C正确,D错误。
故选AC。
三、解答题
17.如图所示,光滑的半球壳半径为R,O点在球心O′的正下方,一小球甲(可视为质点)由距O点很近的A点由静止释放,R 。
(1)若小球甲释放的同时,另一小球乙(可视为质点)从球心O′处自由落下,求两球第一次到达O点的时间比;
(2)若小球甲释放的同时,另一小球丙(可视为质点)在O点正上方某处自由落下,为使两球在O点相碰,小球应由多高处自由落下?
【答案】(1)π∶4;(2) (n=1,2,3)
【解析】 (1)甲球沿圆弧做简谐运动,它第一次到达O点的时间为
乙球做自由落体运动,到达O点的时间为t2,满足
R=gt22
解得
t2=
两球第一次到达O点的时间比为
t1∶t2=π∶4
(2)小球甲从A点由静止释放运动到O点的时间为
t=(2n-1)
其中n满足n=1,2,3,由O点正上方自由落下的小球丙到达O点的时间也为t时两球才能在O点相碰,所以
h=gt2= (n=1,2,3)
18.如图所示为理想单摆,摆角足够小,可认为是简谐运动,其平衡位置记为O点。
(1)若已知摆球的质量为m,摆长为L,在摆角很小时,摆球对于O点的位移x的大小与角对应的弧长近似相等,即近似满足。请推导得出摆球在任意位置处的回复力与位移的比例常数k的表达式。
(2)若仅知道单摆的振幅A及摆球所受回复力与位移的比例常数k,求摆球在振动位移为时的动能(用A和k表示)。
【答案】(1);(2)
【解析】 (1)摆球在位移为x处的受力示意图如答图所示。在摆角很小时,有
在摆球位移为x时,回复力
负号表示F的方向与位移x的方向相反;
即比例常数
(2)摆球在位移x处的势能
摆球在最大振幅处的动能为零,依据能量守恒定律有
则
19.将一测力传感器连接到计算机上就可以测量快速变化的力,如图(a)所示点O为单摆的悬点,将传感器接在摆线与点O之间,现将小球(可视为质点)拉到点A,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中点B为运动最低位置,,小于5°且是未知量。如图(b)所示是由计算得到细线对摆球的拉力大小F随时间变化的图像,且图中时刻为摆球从点A开始运动的时刻,据力学规律和题中信息(g取),求:
(1)单摆的周期和摆长;
(2)摆球的质量及摆动过程中的最大速度。
【答案】(1);0.4m;(2)0.05kg;
【解析】(1)由图(b)可知,该单摆的周期为
根据单摆周期公式
代入数据可求得
(2)单摆在A、C点速度为零,由图(b)可知,此时摆线的拉力最小,则有
B点速度最大,摆线拉力最大,则有
其中
,
从A点到B点,由动能定理有
联立以上式子,代入相关数据求得
,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2.4 单摆 同步练习
一、单选题
1.关于单摆的运动,下列说法正确的是( )
①单摆的回复力是摆线的拉力与重力的合力
②单摆的回复力是重力沿摆球运动轨迹切向的分力
③单摆的周期与摆球质量无关,与振幅无关,与摆长和当地的重力加速度有关
④单摆的运动是简谐运动
⑤在山脚下走时准确的摆钟移到高山上走时将变快
A.③④ B.②③
C.③④⑤ D.①④⑤
2.在盛沙的漏斗下面放一木板,让漏斗左右摆动起来,同时其中细沙匀速流出,经历一段时间后,观察木板上沙子的堆积情况,则沙堆的剖面应是下图中的( )
A. B.
C. D.
3.有一摆长为L的单摆,其悬点正下方某处有一小钉,摆球经过平衡位置向左摆动时,摆线的上部被小钉挡住,使摆长发生变化。现使摆球做小幅度摆动,摆球从右边最高点M运动到左边最高点N的频闪照片如图所示(悬点与小钉未被摄入)。P为摆动中的最低点,已知每相邻两次闪光的时间间隔相等,由此可知,小钉与悬点间的距离为( )
A. B. C. D.无法确定
4.如图甲所示,一单摆悬挂在拉力传感器上。让单摆在竖直面内做小角度摆动,拉力传感器显示绳子拉力的大小随时间的变化图像如图乙所示,已知当地的重力加速度为,则根据图乙中的数据可知( )
A.此单摆的周期
B.此摆球的质量为
C.此单摆的摆长
D.在时刻摆球的回复力最小
5.如图所示,摆长为L的单摆,周期为T.如果在悬点O的正下方的B点固定一个光滑的钉子,OB的距离为OA长度的5/9,使摆球A通过最低点向左摆动,悬线被钉子挡住成为一个新的单摆,则下列说法中正确的是 ( )
A.单摆在整个振动过程中的周期不变
B.单摆在整个振动过程中的周期将变大为原来的6/5倍
C.单摆在整个振动过程中的周期将变小为原来的5/6倍
D.单摆在整个振动过程中的周期无法确定
6.某单摆在竖直平面内做小摆角振动,周期为2 s。如果从摆球向右运动通过平衡位置时开始计时,在t=1.4 s至t=1.5 s的过程中,摆球的( )
A.速度向右在增大,加速度向右在减小
B.速度向左在增大,加速度向左在增大
C.速度向左在减小,加速度向右在增大
D.速度向右在减小,加速度向左在减小
7.如图所示,在两根等长的曲线下悬挂一个小球(可视为质点)组成了所谓的双线摆,若摆长为l,两线与天花板的左、右两侧夹角均为α,当小球垂直纸面做简谐运动时,其周期为( )
A.2π B.2π
C.2π D.2π
8. 如图,长为l的细绳下方悬挂一小球a.绳的另一端固定在天花板上O点处,在O点正下方l的处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图像中,能描述小球在开始一个周期内的x-t关系的是_____.
A. B.C. D.
9.如图所示,单摆甲放在空气中,周期为T甲;单摆乙放在以加速度a(g>a)向下加速的电梯中,周期为T乙;单摆丙带正电荷,放在匀强磁场B中,周期为T丙;单摆丁带正电荷,放在匀强电场E中,周期为T丁,单摆甲、乙、丙及丁的摆长l相同,则下列说法正确的是( )
A.T甲>T乙>T丁>T丙 B.T乙>T甲=T丙>T丁
C.T丙>T甲>T丁>T乙 D.T丁>T甲=T丙>T乙
二、多选题
10.有关单摆下列说法正确的是( )
A.一根橡皮筋一端系在悬点,另一端连接一个小球可以构成一个单摆
B.单摆的摆动一定是简谐运动
C.若单摆在同一平面内摆动,且偏角小于,可以认为单摆的运动是简谐运动
D.单摆做简谐运动时,摆长越大,其运动周期越大
11.以下情况中单摆周期发生变化的有( )
A.将单摆放入匀加速上升的电梯中摆动
B.使摆球带正电,并将摆球放在竖直向下的匀强电场中在竖直平面内摆动
C.使摆球带正电,在悬点放一个带正电的点电荷,使摆球在竖直平面内摆动
D.使摆球带正电,在最低点正下方放一个带负电的点电荷,使摆球在竖直平面内摆动
12.甲、乙两个单摆的振动图象如图所示.根据振动图象可以断定( )
A.若甲、乙两单摆在同一地点摆动,甲、乙两单摆摆长之比是9:4
B.甲、乙两单摆振动的频率之比是3:2
C.甲、乙两单摆振动的周期之比是2:3
D.若甲、乙两单摆在不同一地点摆动,但摆长相同,则甲乙两单摆所在地点的重力加速度之比为9:4
13.惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟。摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制。旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动,如图所示,以下说法正确的是( )
A.当摆钟不准确时需要调整圆盘的位置
B.摆钟快了应使圆盘沿摆杆上移
C.由冬季变为夏季时应使圆盘沿摆杆上移
D.把摆钟从福建移到北京应使 圆盘沿摆杆上移
14.如图所示,长度为l的轻绳上端固定在O点,下端系一小球(小球可以看成质点)。在O点正下方,距O点处的P点固定一颗小钉子。现将小球拉到点A处,轻绳被拉直,然后由静止释放小球。点B是小球运动的最低位置,点C(图中未标出)是小球能够到达的左方最高位置。已知点A与点B之间的高度差为h,h<
B.点C与点B高度差等于h
C.小球摆动的周期等于
D.小球摆动的周期等于
15.甲、乙两位同学分别使用图甲中所示的装置,观察单摆做简谐运动时的振动图像。已知两人实验时所用的摆长相同,落在同一木板上的细砂形成的曲线分别如图乙中、所示。下列关于两图线的分析,正确的是( )
A.对应的细砂摆摆动的幅度较大,对应的细砂摆摆动的幅度较小
B.与对应的细砂摆周期相同
C.对应的木板运动速度比对应的木板运动速度大
D.假设两次实验细砂摆质量相等,则对应的细砂摆摆到最低点时,摆线的拉力比对应的拉力大
16.将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动。用频闪照相机拍到如图所示的单摆从左到右单程过程的频闪照片,以下说法中正确的是( )
A.摆线碰到障碍物前后的摆长之比为9︰4
B.摆线碰到障碍物前后的摆长之比为3︰2
C.摆线经过最低点时,线速度不变,半径减小
D.摆线经过最低点时,角速度变大,半径不变
三、解答题
17.如图所示,光滑的半球壳半径为R,O点在球心O′的正下方,一小球甲(可视为质点)由距O点很近的A点由静止释放,R 。
(1)若小球甲释放的同时,另一小球乙(可视为质点)从球心O′处自由落下,求两球第一次到达O点的时间比;
(2)若小球甲释放的同时,另一小球丙(可视为质点)在O点正上方某处自由落下,为使两球在O点相碰,小球应由多高处自由落下?
18.如图所示为理想单摆,摆角足够小,可认为是简谐运动,其平衡位置记为O点。
(1)若已知摆球的质量为m,摆长为L,在摆角很小时,摆球对于O点的位移x的大小与角对应的弧长近似相等,即近似满足。请推导得出摆球在任意位置处的回复力与位移的比例常数k的表达式。
(2)若仅知道单摆的振幅A及摆球所受回复力与位移的比例常数k,求摆球在振动位移为时的动能(用A和k表示)。
19.将一测力传感器连接到计算机上就可以测量快速变化的力,如图(a)所示点O为单摆的悬点,将传感器接在摆线与点O之间,现将小球(可视为质点)拉到点A,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中点B为运动最低位置,,小于5°且是未知量。如图(b)所示是由计算得到细线对摆球的拉力大小F随时间变化的图像,且图中时刻为摆球从点A开始运动的时刻,据力学规律和题中信息(g取),求:
(1)单摆的周期和摆长;
(2)摆球的质量及摆动过程中的最大速度。
2.4 单 摆
一、单选题
1.关于单摆的运动,下列说法正确的是( )
①单摆的回复力是摆线的拉力与重力的合力
②单摆的回复力是重力沿摆球运动轨迹切向的分力
③单摆的周期与摆球质量无关,与振幅无关,与摆长和当地的重力加速度有关
④单摆的运动是简谐运动
⑤在山脚下走时准确的摆钟移到高山上走时将变快
A.③④ B.②③
C.③④⑤ D.①④⑤
【答案】B
【解析】①②.单摆的回复力是重力沿摆球运动轨迹切向的分力,选项①错误,②正确;
③.根据可知,单摆的周期与摆球质量无关,与振幅无关,与摆长和当地的重力加速度有关,则③正确;
④.单摆在同一平面内摆动,只有当偏角小于5°时,可以认为单摆的运动是简谐运动,则④错误;
⑤.根据,在山脚下走时准确的摆钟移到高山上时,由于重力加速度g变小,则周期变大,则摆钟走时将变慢,⑤错误。故选B。
2.在盛沙的漏斗下面放一木板,让漏斗左右摆动起来,同时其中细沙匀速流出,经历一段时间后,观察木板上沙子的堆积情况,则沙堆的剖面应是下图中的( )
A. B.
C. D.
【答案】B
【解析】不考虑空气阻力,漏斗在从最左端向最右端运动和从最右端向最左端运动时,到达最底端运动速度最快,细沙漏到地面上的最少,两端漏斗运动的最慢,细沙漏到地面上的最多,故选项B正确,选项A、C、D错误;
故选选项B.
3.有一摆长为L的单摆,其悬点正下方某处有一小钉,摆球经过平衡位置向左摆动时,摆线的上部被小钉挡住,使摆长发生变化。现使摆球做小幅度摆动,摆球从右边最高点M运动到左边最高点N的频闪照片如图所示(悬点与小钉未被摄入)。P为摆动中的最低点,已知每相邻两次闪光的时间间隔相等,由此可知,小钉与悬点间的距离为( )
A. B. C. D.无法确定
【答案】C
【解析】设每相邻两次闪光的时间间隔为t,则摆长为L时单摆摆动的周期为
摆长为'时单摆摆动的周期为
所以
T1∶T2=2∶1
又因为
故可得
所以小钉与悬点间的距离为
故选C。
4.如图甲所示,一单摆悬挂在拉力传感器上。让单摆在竖直面内做小角度摆动,拉力传感器显示绳子拉力的大小随时间的变化图像如图乙所示,已知当地的重力加速度为,则根据图乙中的数据可知( )
A.此单摆的周期
B.此摆球的质量为
C.此单摆的摆长
D.在时刻摆球的回复力最小
【答案】C
【解析】A.摆球运动到最低点时,由重力和绳子拉力的合力提供向心力,所以摆球运动到最低点时,绳子拉力最大,则此单摆的周期为
故A错误;
B.摆球运动到最低点时,由重力和绳子拉力的合力提供向心力,则有
此摆球的质量为
故B错误;
C.根据单摆周期公式
可得此单摆的摆长
故C正确;
D.单摆的回复力是重力沿摆球运动轨迹切向的分力提供,摆球运动到最低点时,摆球的回复力最小,所以在时刻摆球的回复力最小,在时刻摆球的回复力最大,故D错误。故选C。
5.如图所示,摆长为L的单摆,周期为T.如果在悬点O的正下方的B点固定一个光滑的钉子,OB的距离为OA长度的5/9,使摆球A通过最低点向左摆动,悬线被钉子挡住成为一个新的单摆,则下列说法中正确的是 ( )
A.单摆在整个振动过程中的周期不变
B.单摆在整个振动过程中的周期将变大为原来的6/5倍
C.单摆在整个振动过程中的周期将变小为原来的5/6倍
D.单摆在整个振动过程中的周期无法确定
【答案】C
【解析】根据单摆周期公式:,未加钉子时,周期:,悬线长变为被挡后,周期变为,所以加了钉子的周期为:,所以周期变为原来的,ABD错误C正确
6.某单摆在竖直平面内做小摆角振动,周期为2 s。如果从摆球向右运动通过平衡位置时开始计时,在t=1.4 s至t=1.5 s的过程中,摆球的( )
A.速度向右在增大,加速度向右在减小
B.速度向左在增大,加速度向左在增大
C.速度向左在减小,加速度向右在增大
D.速度向右在减小,加速度向左在减小
【答案】C
【解析】单摆的周期为2 s,摆球向右通过平衡位置时开始计时,当t=1.4 s时,摆球已通过平衡位置,正在向左方最大位移处做减速运动,由于位移在变大,根据
可知,加速度也在变大,方向向右,C正确。故选C。
7.如图所示,在两根等长的曲线下悬挂一个小球(可视为质点)组成了所谓的双线摆,若摆长为l,两线与天花板的左、右两侧夹角均为α,当小球垂直纸面做简谐运动时,其周期为( )
A.2π B.2π
C.2π D.2π
【答案】D
【解析】根据公式:
T=2π
本题中:
l′=lsin α
所以有:
T=2π.
ABC.由上计算得T为2π,ABC错误;
D. 由上计算得T为2π,D正确
8. 如图,长为l的细绳下方悬挂一小球a.绳的另一端固定在天花板上O点处,在O点正下方l的处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图像中,能描述小球在开始一个周期内的x-t关系的是_____.
A. B.C. D.
【答案】A
【解析】由T=2π得:T1=2π,T2=2π=π=T1 ,故BD错误;
,
由能量守恒定律可知,小球先后摆起得最大高度相同,故l-lcosθ1=
根据数学规律可得: 故,即第一次振幅是第二次振幅得2倍,故A正确,C错误.
9.如图所示,单摆甲放在空气中,周期为T甲;单摆乙放在以加速度a(g>a)向下加速的电梯中,周期为T乙;单摆丙带正电荷,放在匀强磁场B中,周期为T丙;单摆丁带正电荷,放在匀强电场E中,周期为T丁,单摆甲、乙、丙及丁的摆长l相同,则下列说法正确的是( )
A.T甲>T乙>T丁>T丙 B.T乙>T甲=T丙>T丁
C.T丙>T甲>T丁>T乙 D.T丁>T甲=T丙>T乙
【答案】B
【解析】根据单摆公式,对甲摆有
T甲=2π
对乙摆有
T乙=2π
对丙摆,由于摆动过程中洛伦兹力总是垂直于速度方向,故不可能产生沿圆弧切向的分力效果而参与提供回复力,所以周期不变,即
T丙=2π
对丁摆,由于摆球受竖直向下的重力的同时,还受竖直向下的电场力,电场力在圆弧切向产生分力,与重力沿切向的分力一起提供回复力,相当于重力增大了。等效重力
F=mg+qE
故等效重力加速度
故周期
T丁=2π
所以
T乙>T甲=T丙>T丁
ACD错误,B正确。故选B。
二、多选题
10.有关单摆下列说法正确的是( )
A.一根橡皮筋一端系在悬点,另一端连接一个小球可以构成一个单摆
B.单摆的摆动一定是简谐运动
C.若单摆在同一平面内摆动,且偏角小于,可以认为单摆的运动是简谐运动
D.单摆做简谐运动时,摆长越大,其运动周期越大
【答案】CD
【解析】A.一根不可伸长的细绳一端系在悬点,另一端连接一个质量较大体积较小的小球可以构成一个单摆,A错误;
BC.若单摆在同一平面内摆动,且偏角小于5°,可以认为单摆的运动是简谐运动,B错误,C正确;
D.根据可知,单摆做简谐运动时,摆长越大,其运动周期越大,D正确。
故选CD。
11.以下情况中单摆周期发生变化的有( )
A.将单摆放入匀加速上升的电梯中摆动
B.使摆球带正电,并将摆球放在竖直向下的匀强电场中在竖直平面内摆动
C.使摆球带正电,在悬点放一个带正电的点电荷,使摆球在竖直平面内摆动
D.使摆球带正电,在最低点正下方放一个带负电的点电荷,使摆球在竖直平面内摆动
【答案】AB
【解析】A.由
可知,将单摆放入匀加速上升的电梯中,单摆处于超重状态,等效重力加速度变大,周期将减小,故A正确;
B.使摆球带正电,将摆球放在竖直向下的匀强电场中在竖直平面内摆动,摆球受到竖直向下的电场力和重力作用,等效重力加速度变大,周期将减小,故B正确;
CD.在悬点放一个带正电的点电荷,或在最低点正下方放一个带负电的点电荷,使摆球在竖直平面内摆动,正点电荷或负点电荷在一个周期内对摆球做的功均为0,周期将不变,故C、D错误。
故选AB。
12.甲、乙两个单摆的振动图象如图所示.根据振动图象可以断定( )
A.若甲、乙两单摆在同一地点摆动,甲、乙两单摆摆长之比是9:4
B.甲、乙两单摆振动的频率之比是3:2
C.甲、乙两单摆振动的周期之比是2:3
D.若甲、乙两单摆在不同一地点摆动,但摆长相同,则甲乙两单摆所在地点的重力加速度之比为9:4
【答案】BCD
【解析】ABC.根据图像可知,单摆振动的周期关系
所以周期之比为
频率为周期的反比,所以频率之比
若甲乙在同一地点,则重力加速度相同,根据周期公式
所以摆长之比为4:9,A错误BC正确;
D.若在不同地点,摆长相同,根据
得重力加速度之比为9:4,D正确。故选BCD。
13.惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟。摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制。旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动,如图所示,以下说法正确的是( )
A.当摆钟不准确时需要调整圆盘的位置
B.摆钟快了应使圆盘沿摆杆上移
C.由冬季变为夏季时应使圆盘沿摆杆上移
D.把摆钟从福建移到北京应使 圆盘沿摆杆上移
【答案】AC
【解析】A.根据周期公式,当摆钟不准确时,则需要调整摆长,A正确;
B.摆钟快了,周期小,则需将摆长增加,增大周期,B错误;
C.由冬季变为夏季时摆杆受热伸长,则需上移调节,C正确;
D.摆钟从福建移到北京,加速度增大,则需将摆长增加,D错误。
故选AC。
14.如图所示,长度为l的轻绳上端固定在O点,下端系一小球(小球可以看成质点)。在O点正下方,距O点处的P点固定一颗小钉子。现将小球拉到点A处,轻绳被拉直,然后由静止释放小球。点B是小球运动的最低位置,点C(图中未标出)是小球能够到达的左方最高位置。已知点A与点B之间的高度差为h,h<
B.点C与点B高度差等于h
C.小球摆动的周期等于
D.小球摆动的周期等于
【答案】BC
【解析】AB.小球摆动过程中,只有重力做功,机械能守恒,两侧最高点动能均为零,故重力势能也相等,故最大高度相同,故A错误,B正确;
CD.小球B→A→B的时间为
小球B→C→B的时间为
故小球摆动的周期为
故C正确,D错误。故选BC。
15.甲、乙两位同学分别使用图甲中所示的装置,观察单摆做简谐运动时的振动图像。已知两人实验时所用的摆长相同,落在同一木板上的细砂形成的曲线分别如图乙中、所示。下列关于两图线的分析,正确的是( )
A.对应的细砂摆摆动的幅度较大,对应的细砂摆摆动的幅度较小
B.与对应的细砂摆周期相同
C.对应的木板运动速度比对应的木板运动速度大
D.假设两次实验细砂摆质量相等,则对应的细砂摆摆到最低点时,摆线的拉力比对应的拉力大
【答案】BC
【解析】A.由题图乙可知,对应的细砂摆摆动的幅度与对应的细砂摆摆动的幅度相同,故A错误;
B.由单摆周期公式
及两摆摆长相同可知,周期相同,故B正确;
C.由题图乙可知,若对应的木板的运动时间为,则对应的木板的运动时间为,可知对应的木板运动速度比对应的木板运动速度大,故C正确;
D.由动能定理有
在最低点有
解得
由于两摆的振动幅度相同,则相同,故拉力相同,故D错误。
故选BC。
16.将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动。用频闪照相机拍到如图所示的单摆从左到右单程过程的频闪照片,以下说法中正确的是( )
A.摆线碰到障碍物前后的摆长之比为9︰4
B.摆线碰到障碍物前后的摆长之比为3︰2
C.摆线经过最低点时,线速度不变,半径减小
D.摆线经过最低点时,角速度变大,半径不变
【答案】AC
【解析】AB.频闪照片拍摄的时间间隔一定,由图可知,摆线与障碍物碰撞前后的周期之比为3:2,根据单摆的周期公式得,摆长之比为9:4,故A正确,B错误;
CD.摆线碰到障碍物的瞬间,摆球的速度不能发生突变,即线速度不变。根据v=rω可知,摆球转动的半径减小,线速度不变,所以角速度增大,故C正确,D错误。
故选AC。
三、解答题
17.如图所示,光滑的半球壳半径为R,O点在球心O′的正下方,一小球甲(可视为质点)由距O点很近的A点由静止释放,R 。
(1)若小球甲释放的同时,另一小球乙(可视为质点)从球心O′处自由落下,求两球第一次到达O点的时间比;
(2)若小球甲释放的同时,另一小球丙(可视为质点)在O点正上方某处自由落下,为使两球在O点相碰,小球应由多高处自由落下?
【答案】(1)π∶4;(2) (n=1,2,3)
【解析】 (1)甲球沿圆弧做简谐运动,它第一次到达O点的时间为
乙球做自由落体运动,到达O点的时间为t2,满足
R=gt22
解得
t2=
两球第一次到达O点的时间比为
t1∶t2=π∶4
(2)小球甲从A点由静止释放运动到O点的时间为
t=(2n-1)
其中n满足n=1,2,3,由O点正上方自由落下的小球丙到达O点的时间也为t时两球才能在O点相碰,所以
h=gt2= (n=1,2,3)
18.如图所示为理想单摆,摆角足够小,可认为是简谐运动,其平衡位置记为O点。
(1)若已知摆球的质量为m,摆长为L,在摆角很小时,摆球对于O点的位移x的大小与角对应的弧长近似相等,即近似满足。请推导得出摆球在任意位置处的回复力与位移的比例常数k的表达式。
(2)若仅知道单摆的振幅A及摆球所受回复力与位移的比例常数k,求摆球在振动位移为时的动能(用A和k表示)。
【答案】(1);(2)
【解析】 (1)摆球在位移为x处的受力示意图如答图所示。在摆角很小时,有
在摆球位移为x时,回复力
负号表示F的方向与位移x的方向相反;
即比例常数
(2)摆球在位移x处的势能
摆球在最大振幅处的动能为零,依据能量守恒定律有
则
19.将一测力传感器连接到计算机上就可以测量快速变化的力,如图(a)所示点O为单摆的悬点,将传感器接在摆线与点O之间,现将小球(可视为质点)拉到点A,此时细线处于张紧状态,释放摆球,则摆球在竖直平面内的ABC之间来回摆动,其中点B为运动最低位置,,小于5°且是未知量。如图(b)所示是由计算得到细线对摆球的拉力大小F随时间变化的图像,且图中时刻为摆球从点A开始运动的时刻,据力学规律和题中信息(g取),求:
(1)单摆的周期和摆长;
(2)摆球的质量及摆动过程中的最大速度。
【答案】(1);0.4m;(2)0.05kg;
【解析】(1)由图(b)可知,该单摆的周期为
根据单摆周期公式
代入数据可求得
(2)单摆在A、C点速度为零,由图(b)可知,此时摆线的拉力最小,则有
B点速度最大,摆线拉力最大,则有
其中
,
从A点到B点,由动能定理有
联立以上式子,代入相关数据求得
,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
