8.3简单几何体的表面积与体积 同步训练(含解析)
文档属性
| 名称 | 8.3简单几何体的表面积与体积 同步训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 806.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 08:55:55 | ||
图片预览

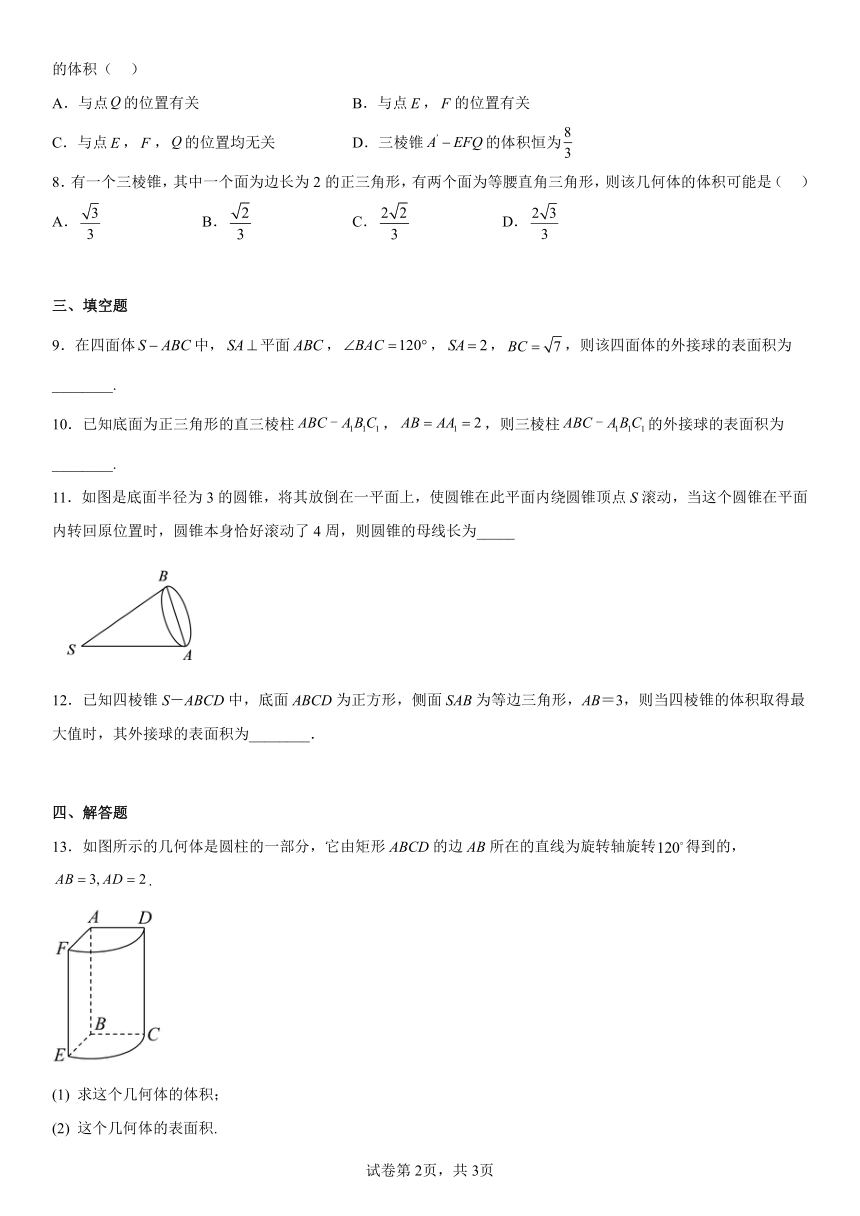
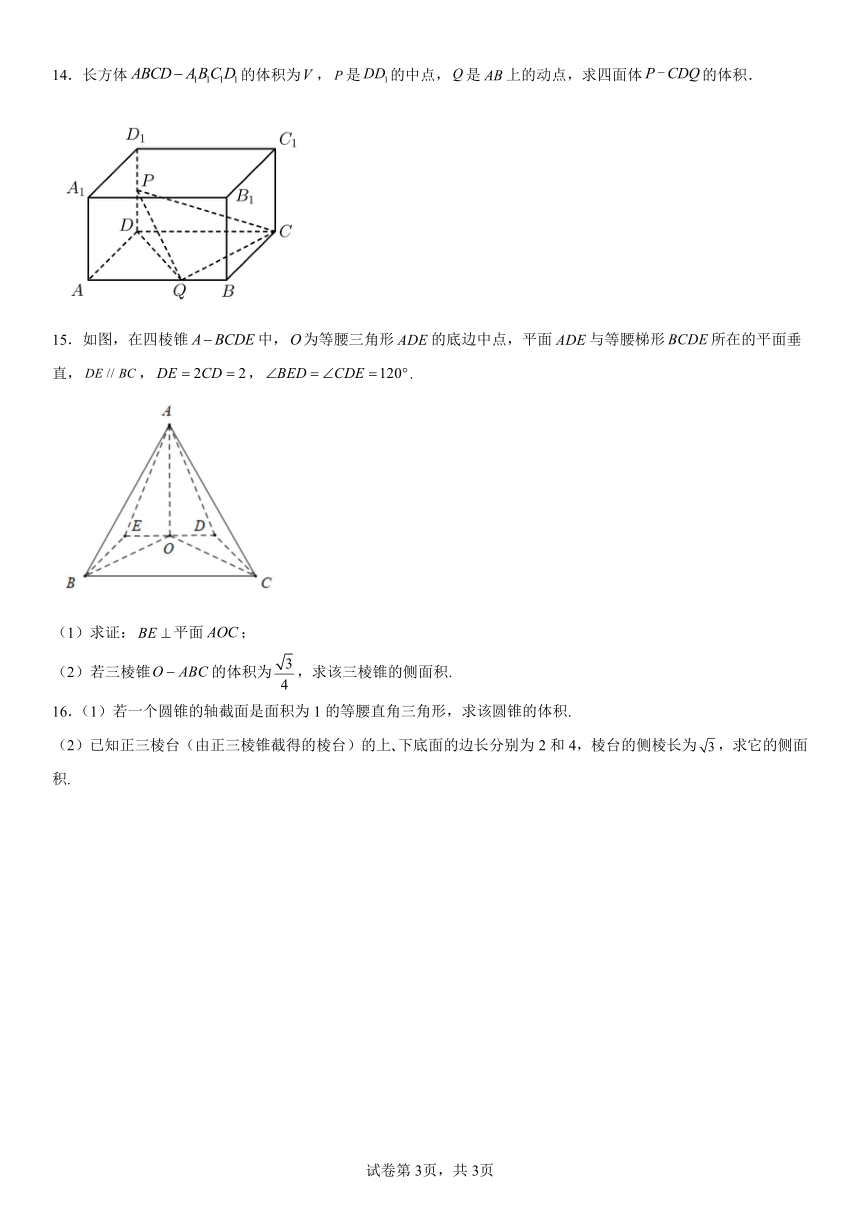


文档简介
8.3简单几何体的表面积与体积 同步训练
一、单选题
1.已知三棱柱的体积为1,、Q、R分别为侧棱、、上的点且,则( )
A. B. C. D.
2.过圆锥的轴作截面,如果截面为正三角形,则称该圆锥为等边圆锥.已知在一等边圆锥中,过顶点P的截面与底面交于CD,若∠COD=90°(O为底面圆心),且,则这个等边圆锥的表面积为( )
A.2π+π B.3π
C.2π+π D.π+π
3.已知正方形ABCD的边长为2,沿对角线AC将向上折起,构成四面体ABCD,则该四面体ABCD外接球的表面积为( )
A. B. C. D.
4.若圆台的高是3,一个底面半径是另一个底面半径的2倍,母线与下底面成角,则这个圆台的侧面积是( )
A. B.
C. D.
5.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,凸出部分叫榫,凹进部分叫卯,榫和卯合,起到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如图所示是一种榫卯的三视图,则该空间几何体的表面积为( )
A.192 B.186 C.180 D.198
6.已知四棱锥的侧棱长均为3,底面是边长为2的正方形,则该四棱锥表面积为( )
A.12 B.16 C. D.
二、多选题
7.正方体的棱长为4,动点,在棱上,,动点在棱上,则三棱锥的体积( )
A.与点的位置有关 B.与点,的位置有关
C.与点,,的位置均无关 D.三棱锥的体积恒为
8.有一个三棱锥,其中一个面为边长为2的正三角形,有两个面为等腰直角三角形,则该几何体的体积可能是( )
A. B. C. D.
三、填空题
9.在四面体中,平面,,,,则该四面体的外接球的表面积为________.
10.已知底面为正三角形的直三棱柱,,则三棱柱的外接球的表面积为________.
11.如图是底面半径为3的圆锥,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点S滚动,当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了4周,则圆锥的母线长为_____
12.已知四棱锥S-ABCD中,底面ABCD为正方形,侧面SAB为等边三角形,AB=3,则当四棱锥的体积取得最大值时,其外接球的表面积为________.
四、解答题
13.如图所示的几何体是圆柱的一部分,它由矩形ABCD的边AB所在的直线为旋转轴旋转得到的,.
(1) 求这个几何体的体积;
(2) 这个几何体的表面积.
14.长方体的体积为,是的中点,是上的动点,求四面体的体积.
15.如图,在四棱锥中,为等腰三角形的底边中点,平面与等腰梯形所在的平面垂直,,,.
(1)求证:平面;
(2)若三棱锥的体积为,求该三棱锥的侧面积.
16.(1)若一个圆锥的轴截面是面积为1的等腰直角三角形,求该圆锥的体积.
(2)已知正三棱台(由正三棱锥截得的棱台)的上 下底面的边长分别为2和4,棱台的侧棱长为,求它的侧面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】由题意,根据线段的等量关系,可得面积的等量关系,结合棱锥的体积公式,进行等积变换,根据同底同高的棱柱与棱锥之间的体积关系,可得答案.
【详解】解:在三棱柱中,易知侧面为平行四边形,设其面积为,上的高为,
在平行四边形中,易知四边形为梯形或平行四边形,设其面积为,且其高为,
则,
在三棱柱中,易知平面,点到平面的距离与点到平面的距离,设该距离为,
连接,作图如下:
则,
设三棱柱的体积,由图可知,,即,
故选:B.
2.B
【详解】如图,连接PO,设圆锥的母线长为2a,则圆锥的底面圆的半径为a,高为PO=.
由已知得CD=,PC=PD=2a.
所以为等腰三角形,设其底边上的高为,
则,
则,
从而a=1.
所以圆锥的表面积为.
故选:B
3.B
【分析】直接确定球心的位置再求解即可
【详解】设正方形ABCD的对角线交于点,由正方形的性质可得,翻折后四面体满足,故为该四面体ABCD外接球的球心,故球的半径,故其表面积
故选:B
【点睛】本题主要考查了外接球的问题,重点是根据球心的性质确定球心的位置,再利用公式求解,属于基础题
4.B
【分析】由题意,作该圆台的轴截面,求得上下底面半径和母线长,根据侧面积计算公式,可得答案.
【详解】由题意,可作该圆台的轴截面,如下图所示:
则圆台的高,
上底面半径,下底面半径,即,
母线,即,
在中,,,
易知在正方形中,,则,即,
综上,,
圆台的侧面积.
故选:B.
5.A
【分析】由三视图还原原几何体,可知该几何体为组合体,上部分是长方体,棱长分别为,下部分为长方体,棱长分别为,再由表面积公式求解
【详解】
由三视图还原原几何体,可知该几何体为组合体,上部分是长方体,棱长分别为,下部分为长方体,棱长分别为,
其表面积为,
故选:
6.C
【分析】根据题意该四棱锥的四个侧面为全等的等腰三角形,在底面的一条边上取中点利用等腰三角形的三线合一定理,结合勾股定理可求出三角形的面积,从而可得侧面积,进一步可得到答案.
【详解】设四棱锥满足侧棱长均为3,底面是边长为2的正方形
所以侧面为全等的等腰三角形.
所以该四棱锥的侧面积为,取的中点
在中,,
所以,且,所以
所以
故该四棱锥表面积为
故选:C
7.CD
【分析】由等体积法结合体积公式判断即可.
【详解】解:,的面积为定值,
点到所在平面的距离为定值4,
故三棱锥的体积与点,,位置均无关,是定值.
故选:CD.
8.BCD
【分析】分三种情况讨论,作出图形,确定三棱锥中每条棱的长度,即可求出其体积.
【详解】如图所示:
①若平面,为边长为2的正三角形,,,都是等腰直角三角形,满足题目条件,故其体积;
②若平面,为边长为2的正三角形,,,都是等腰直角三角形,满足题目条件,故其体积;
③若为边长为2的正三角形,,都是等腰直角三角形,,,满足题目条件,取中点,因为,而,所以,即有平面,故其体积为;
故选:BCD
9.
【解析】在中,利用正弦定理,求得外接圆直径为,再结合球的性质,求得球的半径,进而求得外接球的表面积,得到答案.
【详解】在中,因为,,
可得的外圆球直径为,
又由球的性质,可得,
所以球的表面积为.
故答案为:.
【点睛】运用公式(为底面多边形的外接圆的半径,为几何体的外接球的半径,表示球心到底面的距离)求得球的半径,该公式是求解球的半径的常用公式,该方法的实质是通过寻找外接球的一个轴截面,把立体几何问题转化为平面几何问题来研究.
10.
【解析】利用正弦定理求出的外接圆直径,进而可得出该三棱柱的外接球直径为,利用球体的表面积公式即可求得结果.
【详解】如下图所示,设圆柱的底面半径为,母线长为,圆柱的外接球半径为,
取圆柱的轴截面,则该圆柱的轴截面矩形的对角线的中点到圆柱底面圆上每个点的距离都等于,则为圆柱的外接球球心,由勾股定理可得.
本题中,设的外接圆为圆,可将正三棱柱内接于圆柱,如下图所示:
的外接圆直径为,圆柱的母线长为,
所以,正三棱柱的外接球,即圆柱的外接球直径为,
因此,三棱柱的外接球的表面积为.
故答案为:.
【点睛】方法点睛:求空间多面体的外接球半径的常用方法:
①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;
②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;
③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.
11.12
【分析】设圆锥的母线长为l,求出以S为圆心,SA为半径的圆的面积以及圆锥的侧面积,根据题意,列出方程即可求得答案.
【详解】设圆锥的母线长为l,则以S为圆心,SA为半径的圆的面积为,
又圆锥的侧面积为,
因为当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了4周,
所以,解得,
故答案为:12
12.
【分析】根据题意可知侧面底面ABCD,然后结合图形由底面外接圆半径、球心到底面的距离和球的半径满足勾股定理可得.
【详解】依题意可知,当侧面底面ABCD时,四棱锥S-ABCD的体积最大.
设球心为O,半径为R,正方形ABCD和外接圆的圆心分别为,,正方形ABCD外接圆半径为,则平面ABCD,平面SAB.
因为和正方形ABCD的边长均为3,设AB的中点为E,
所以,,
由勾股定理得,
所以球O的表面积.
故答案为:
13.(1);
(2).
【分析】(1)求出矩形旋转一周所得圆柱的体积,根据几何体与圆柱体积比求其体积即可;
(2)分别求出几何体外侧曲面、上下底面、两个矩形的面积,进而加总即可得结果.
【详解】(1)由题设,若将矩形旋转一周所得圆柱的体积为,
其中为底面积,且,故,
因为几何体是矩形旋转得到,故几何体体积为.
(2)由题设,则几何体外侧曲面的面积为,
上下底面的面积和为,矩形的面积和为,
综上,几何体的表面积为.
14..
【分析】因为是上的动点,且,可求出,再根据,即可求出四面体的体积.
【详解】设长方体的长、宽、高分别为,,,则有.
是的中点,所以,
因为是上的动点,且,所以,
所以.
15.(1)证明见解析;(2)
【分析】(1)过点,作,交于,证明,再证明,即可得证;
(2)分别计算三个侧面三角形的面积求和即可.
【详解】(1)过点,作,交于.
由已知得,,
所以
因为,所以,
所以,
所以,所以.
由已知得,
因为平面平面,平面平面,平面,
所以平面,所以,
因为,平面.
(2)在中,由余弦定理可得,同理,因为,
所以,
又因为
所以
所以,
所以,
所以三棱锥的侧面积为.
【点睛】本题主要考查了线面垂直,线线垂直的证明,三棱锥的侧面积,属于中档题.
16.(1);(2).
【分析】(1)由圆锥轴截面的面积求出圆锥的高和底面半径,再由圆锥体积公式求体积.
(2)过点B作BM⊥B1C1于点M,根据正棱台的特征求出侧面的高,进而求侧面积.
【详解】(1)设圆锥底面圆的半径为r,高为h,母线长为l,
由题意,得,则,
,,故.
(2)如图,作出正三棱台,
过点B作BM⊥B1C1于点M,
在Rt△BB1M中,B1M=1,BB1=,故BM==,
所以侧面积为3××(2+4)×=.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知三棱柱的体积为1,、Q、R分别为侧棱、、上的点且,则( )
A. B. C. D.
2.过圆锥的轴作截面,如果截面为正三角形,则称该圆锥为等边圆锥.已知在一等边圆锥中,过顶点P的截面与底面交于CD,若∠COD=90°(O为底面圆心),且,则这个等边圆锥的表面积为( )
A.2π+π B.3π
C.2π+π D.π+π
3.已知正方形ABCD的边长为2,沿对角线AC将向上折起,构成四面体ABCD,则该四面体ABCD外接球的表面积为( )
A. B. C. D.
4.若圆台的高是3,一个底面半径是另一个底面半径的2倍,母线与下底面成角,则这个圆台的侧面积是( )
A. B.
C. D.
5.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,凸出部分叫榫,凹进部分叫卯,榫和卯合,起到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如图所示是一种榫卯的三视图,则该空间几何体的表面积为( )
A.192 B.186 C.180 D.198
6.已知四棱锥的侧棱长均为3,底面是边长为2的正方形,则该四棱锥表面积为( )
A.12 B.16 C. D.
二、多选题
7.正方体的棱长为4,动点,在棱上,,动点在棱上,则三棱锥的体积( )
A.与点的位置有关 B.与点,的位置有关
C.与点,,的位置均无关 D.三棱锥的体积恒为
8.有一个三棱锥,其中一个面为边长为2的正三角形,有两个面为等腰直角三角形,则该几何体的体积可能是( )
A. B. C. D.
三、填空题
9.在四面体中,平面,,,,则该四面体的外接球的表面积为________.
10.已知底面为正三角形的直三棱柱,,则三棱柱的外接球的表面积为________.
11.如图是底面半径为3的圆锥,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点S滚动,当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了4周,则圆锥的母线长为_____
12.已知四棱锥S-ABCD中,底面ABCD为正方形,侧面SAB为等边三角形,AB=3,则当四棱锥的体积取得最大值时,其外接球的表面积为________.
四、解答题
13.如图所示的几何体是圆柱的一部分,它由矩形ABCD的边AB所在的直线为旋转轴旋转得到的,.
(1) 求这个几何体的体积;
(2) 这个几何体的表面积.
14.长方体的体积为,是的中点,是上的动点,求四面体的体积.
15.如图,在四棱锥中,为等腰三角形的底边中点,平面与等腰梯形所在的平面垂直,,,.
(1)求证:平面;
(2)若三棱锥的体积为,求该三棱锥的侧面积.
16.(1)若一个圆锥的轴截面是面积为1的等腰直角三角形,求该圆锥的体积.
(2)已知正三棱台(由正三棱锥截得的棱台)的上 下底面的边长分别为2和4,棱台的侧棱长为,求它的侧面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】由题意,根据线段的等量关系,可得面积的等量关系,结合棱锥的体积公式,进行等积变换,根据同底同高的棱柱与棱锥之间的体积关系,可得答案.
【详解】解:在三棱柱中,易知侧面为平行四边形,设其面积为,上的高为,
在平行四边形中,易知四边形为梯形或平行四边形,设其面积为,且其高为,
则,
在三棱柱中,易知平面,点到平面的距离与点到平面的距离,设该距离为,
连接,作图如下:
则,
设三棱柱的体积,由图可知,,即,
故选:B.
2.B
【详解】如图,连接PO,设圆锥的母线长为2a,则圆锥的底面圆的半径为a,高为PO=.
由已知得CD=,PC=PD=2a.
所以为等腰三角形,设其底边上的高为,
则,
则,
从而a=1.
所以圆锥的表面积为.
故选:B
3.B
【分析】直接确定球心的位置再求解即可
【详解】设正方形ABCD的对角线交于点,由正方形的性质可得,翻折后四面体满足,故为该四面体ABCD外接球的球心,故球的半径,故其表面积
故选:B
【点睛】本题主要考查了外接球的问题,重点是根据球心的性质确定球心的位置,再利用公式求解,属于基础题
4.B
【分析】由题意,作该圆台的轴截面,求得上下底面半径和母线长,根据侧面积计算公式,可得答案.
【详解】由题意,可作该圆台的轴截面,如下图所示:
则圆台的高,
上底面半径,下底面半径,即,
母线,即,
在中,,,
易知在正方形中,,则,即,
综上,,
圆台的侧面积.
故选:B.
5.A
【分析】由三视图还原原几何体,可知该几何体为组合体,上部分是长方体,棱长分别为,下部分为长方体,棱长分别为,再由表面积公式求解
【详解】
由三视图还原原几何体,可知该几何体为组合体,上部分是长方体,棱长分别为,下部分为长方体,棱长分别为,
其表面积为,
故选:
6.C
【分析】根据题意该四棱锥的四个侧面为全等的等腰三角形,在底面的一条边上取中点利用等腰三角形的三线合一定理,结合勾股定理可求出三角形的面积,从而可得侧面积,进一步可得到答案.
【详解】设四棱锥满足侧棱长均为3,底面是边长为2的正方形
所以侧面为全等的等腰三角形.
所以该四棱锥的侧面积为,取的中点
在中,,
所以,且,所以
所以
故该四棱锥表面积为
故选:C
7.CD
【分析】由等体积法结合体积公式判断即可.
【详解】解:,的面积为定值,
点到所在平面的距离为定值4,
故三棱锥的体积与点,,位置均无关,是定值.
故选:CD.
8.BCD
【分析】分三种情况讨论,作出图形,确定三棱锥中每条棱的长度,即可求出其体积.
【详解】如图所示:
①若平面,为边长为2的正三角形,,,都是等腰直角三角形,满足题目条件,故其体积;
②若平面,为边长为2的正三角形,,,都是等腰直角三角形,满足题目条件,故其体积;
③若为边长为2的正三角形,,都是等腰直角三角形,,,满足题目条件,取中点,因为,而,所以,即有平面,故其体积为;
故选:BCD
9.
【解析】在中,利用正弦定理,求得外接圆直径为,再结合球的性质,求得球的半径,进而求得外接球的表面积,得到答案.
【详解】在中,因为,,
可得的外圆球直径为,
又由球的性质,可得,
所以球的表面积为.
故答案为:.
【点睛】运用公式(为底面多边形的外接圆的半径,为几何体的外接球的半径,表示球心到底面的距离)求得球的半径,该公式是求解球的半径的常用公式,该方法的实质是通过寻找外接球的一个轴截面,把立体几何问题转化为平面几何问题来研究.
10.
【解析】利用正弦定理求出的外接圆直径,进而可得出该三棱柱的外接球直径为,利用球体的表面积公式即可求得结果.
【详解】如下图所示,设圆柱的底面半径为,母线长为,圆柱的外接球半径为,
取圆柱的轴截面,则该圆柱的轴截面矩形的对角线的中点到圆柱底面圆上每个点的距离都等于,则为圆柱的外接球球心,由勾股定理可得.
本题中,设的外接圆为圆,可将正三棱柱内接于圆柱,如下图所示:
的外接圆直径为,圆柱的母线长为,
所以,正三棱柱的外接球,即圆柱的外接球直径为,
因此,三棱柱的外接球的表面积为.
故答案为:.
【点睛】方法点睛:求空间多面体的外接球半径的常用方法:
①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;
②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;
③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.
11.12
【分析】设圆锥的母线长为l,求出以S为圆心,SA为半径的圆的面积以及圆锥的侧面积,根据题意,列出方程即可求得答案.
【详解】设圆锥的母线长为l,则以S为圆心,SA为半径的圆的面积为,
又圆锥的侧面积为,
因为当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了4周,
所以,解得,
故答案为:12
12.
【分析】根据题意可知侧面底面ABCD,然后结合图形由底面外接圆半径、球心到底面的距离和球的半径满足勾股定理可得.
【详解】依题意可知,当侧面底面ABCD时,四棱锥S-ABCD的体积最大.
设球心为O,半径为R,正方形ABCD和外接圆的圆心分别为,,正方形ABCD外接圆半径为,则平面ABCD,平面SAB.
因为和正方形ABCD的边长均为3,设AB的中点为E,
所以,,
由勾股定理得,
所以球O的表面积.
故答案为:
13.(1);
(2).
【分析】(1)求出矩形旋转一周所得圆柱的体积,根据几何体与圆柱体积比求其体积即可;
(2)分别求出几何体外侧曲面、上下底面、两个矩形的面积,进而加总即可得结果.
【详解】(1)由题设,若将矩形旋转一周所得圆柱的体积为,
其中为底面积,且,故,
因为几何体是矩形旋转得到,故几何体体积为.
(2)由题设,则几何体外侧曲面的面积为,
上下底面的面积和为,矩形的面积和为,
综上,几何体的表面积为.
14..
【分析】因为是上的动点,且,可求出,再根据,即可求出四面体的体积.
【详解】设长方体的长、宽、高分别为,,,则有.
是的中点,所以,
因为是上的动点,且,所以,
所以.
15.(1)证明见解析;(2)
【分析】(1)过点,作,交于,证明,再证明,即可得证;
(2)分别计算三个侧面三角形的面积求和即可.
【详解】(1)过点,作,交于.
由已知得,,
所以
因为,所以,
所以,
所以,所以.
由已知得,
因为平面平面,平面平面,平面,
所以平面,所以,
因为,平面.
(2)在中,由余弦定理可得,同理,因为,
所以,
又因为
所以
所以,
所以,
所以三棱锥的侧面积为.
【点睛】本题主要考查了线面垂直,线线垂直的证明,三棱锥的侧面积,属于中档题.
16.(1);(2).
【分析】(1)由圆锥轴截面的面积求出圆锥的高和底面半径,再由圆锥体积公式求体积.
(2)过点B作BM⊥B1C1于点M,根据正棱台的特征求出侧面的高,进而求侧面积.
【详解】(1)设圆锥底面圆的半径为r,高为h,母线长为l,
由题意,得,则,
,,故.
(2)如图,作出正三棱台,
过点B作BM⊥B1C1于点M,
在Rt△BB1M中,B1M=1,BB1=,故BM==,
所以侧面积为3××(2+4)×=.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
