2.1.1直线的倾斜角与斜率(共31张ppt)
文档属性
| 名称 | 2.1.1直线的倾斜角与斜率(共31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
《直线的倾斜角与斜率》
《直线的倾斜角与斜率》
年 级:高二年级
学 科:数学(人教版)
主讲人:田方舒
学 校:湖南省株洲市渌口区第三中学
高二年级 | 数学
导语
学生自学章引言的内容
问题1:在平面直角坐标系中,表示点用什么表示?直线用什么表示?
下面,我们从研究直线的倾斜角和斜率开 始探究解析几何的世界.
点——坐标
直线——方程
问题2:如何用坐标表示直线呢?
高二年级 | 数学
数学问题引入(一)
问题1:在平面几何中,确定直线的条件是什么?对于平面直角坐标系内的一条直线,它的位置由哪些条件确定?
问题2:在平面直角坐标系内给一个点,过这个点有无数条直线。
再给一个什么条件就可以唯一确定一条直线呢?
请学生手动操作体验
高二年级 | 数学
数学概念
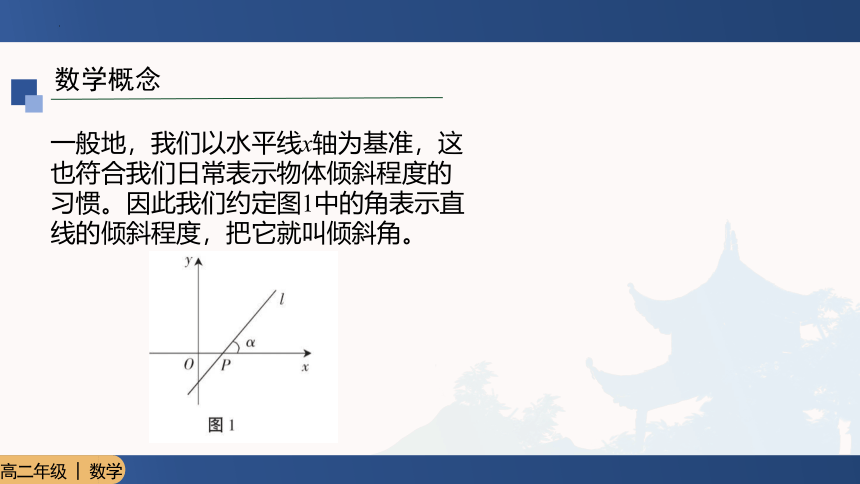
一般地,我们以水平线x轴为基准,这也符合我们日常表示物体倾斜程度的习惯。因此我们约定图1中的角表示直线的倾斜程度,把它就叫倾斜角。
高二年级 | 数学
数学概念
当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角。
高二年级 | 数学
数学概念
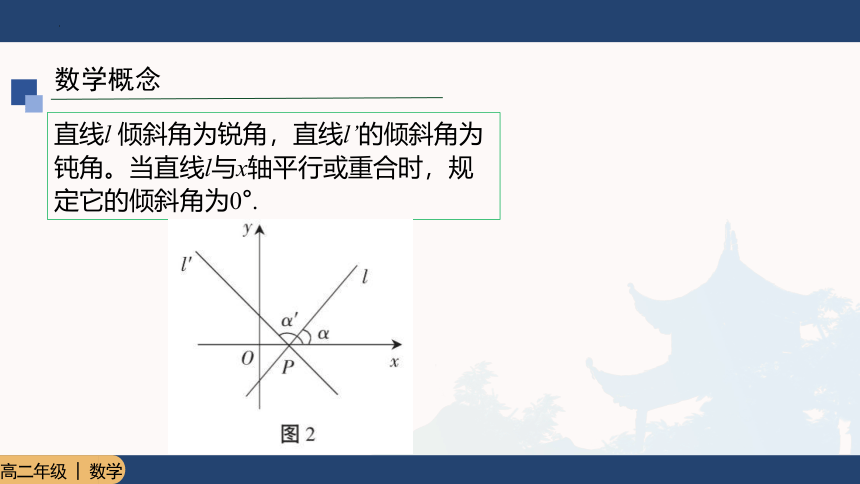
直线l 倾斜角为锐角,直线l’的倾斜角为钝角。当直线l与x轴平行或重合时,规定它的倾斜角为0°.
高二年级 | 数学
数学问题
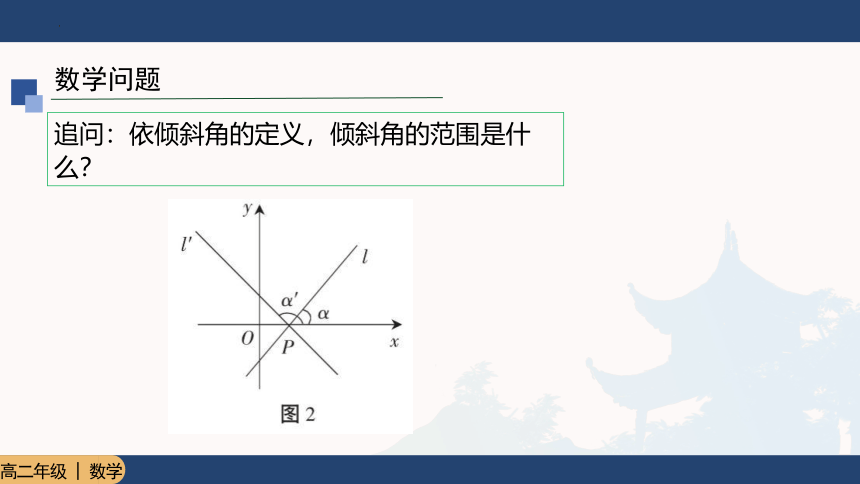
追问:依倾斜角的定义,倾斜角的范围是什么?
高二年级 | 数学
数学概念
倾斜角的几何意义:
(1)从运动变化的观点来看,当直线l与x轴相交时,直线l的倾斜角是由x轴绕直线l与x轴的交点按逆时针方向旋转到与直线l重合时所得到的最小正角.
(2)倾斜角从“形”的方面直观地体现了直线对x轴正向的倾斜程度.
直线的倾斜角α的取值范围:0°≤α<180°。
高二年级 | 数学
数学概念问题剖析
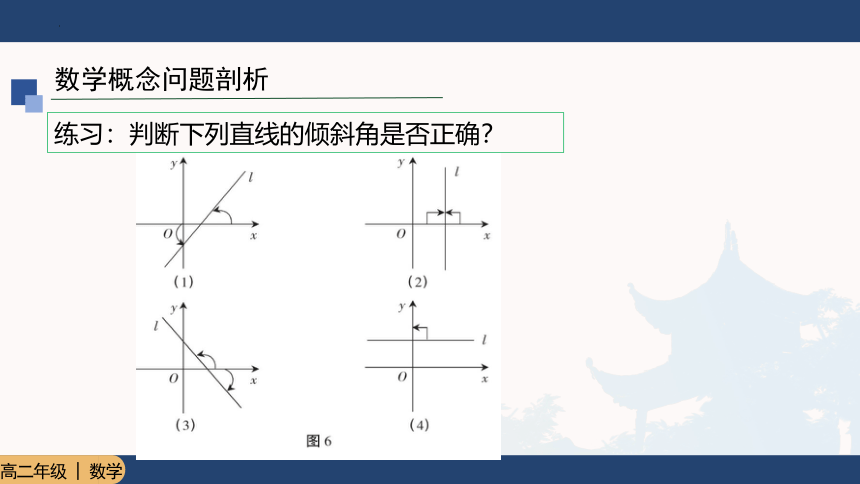
练习:判断下列直线的倾斜角是否正确?
高二年级 | 数学
数学情景引入(二)
交通工程上一般用“坡度”来描述一段道路对于水平
方向的倾斜程度,如图,一辆汽车沿某条道路从A点
前进到B点,在水平方向前进的距离为AD,竖直方
向上升的高度为DB(如果是下降,则DB的值为负实数),
则坡度k= 若k>0,则表示上坡,若k<0,
则表示下坡,为了实际应用与安全,在道路铺设时常
要规划坡度的大小.那么“坡度”是如何来刻画道路
的倾斜程度的呢?
高二年级 | 数学
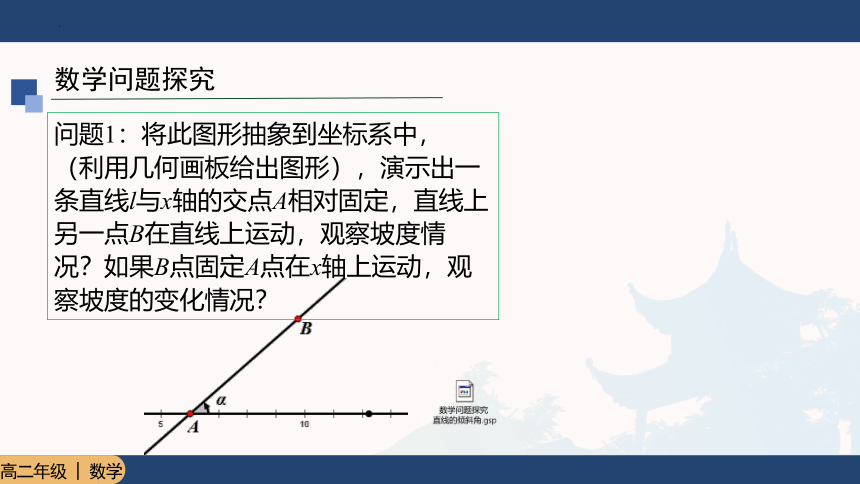
数学问题探究
问题1:将此图形抽象到坐标系中,(利用几何画板给出图形),演示出一条直线l与x轴的交点A相对固定,直线上另一点B在直线上运动,观察坡度情况?如果B点固定A点在x轴上运动,观察坡度的变化情况?
高二年级 | 数学
数学概念
把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即
k=tan α.
高二年级 | 数学
数学问题引入(三)
由于两点可以确定一条直线,那么我们直线上任取两点P1(x1,y1),P2(x2,y2),x1≠x2,可知直线l由P1,P2唯一确定。所以,可以推断,直线l的倾斜角一定与P1,P2两点的坐标有内在联系的。
高二年级 | 数学
数学问题探究
问题1:在平面直角坐标系中,设直线l的倾斜角为α.(教材52页问题探究)
(1)已知直线l 经过O(0,0),P( ,1),α与O,P的坐标有什么关系?
高二年级 | 数学
数学问题探究
问题1:在平面直角坐标系中,设直线l的倾斜角为α.(教材52页问题探究)
(2)类似地,如果直线l经过P1(-1,1),P2( ,0),α与P1,P2的坐标有什么关系?
高二年级 | 数学
数学问题探究
问题1:在平面直角坐标系中,设直线l的倾斜角为α.(教材52页问题探究)
(3)一般地,如果直线l经过两点P1(x1,y1),P2(x2,y2),x1≠x2,那么α与P1,P2的坐标有什么关系?
高二年级 | 数学
数学公式
如果直线l经过两点P1(x1,y1),P2(x2,y2),x1≠x2,可得斜率公式:
高二年级 | 数学
知识拓展
直线P1P2上的向量 以及与它平行的非零
向量都是直线的方向向量。直线P1P2的方向向
量 的坐标为(x2-x1,y2-y1)直线P1P2与x轴
不垂直时,x1≠x2.此时向量 也是直
线P1P2的方向向量,且它的坐标为
,
其中k是直线P1P2的斜率.
高二年级 | 数学
知识拓展
若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则
高二年级 | 数学
例题解析
例1: 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角?
高二年级 | 数学
例题解析
解析:
解析:由kAB>0,kCA>0可知,
直线AB与CA的 倾斜角为锐角,kBC<0,直线BC倾斜角为钝角。
高二年级 | 数学
数学问题引入(四)
问题1:是否每条直线都有斜率?倾斜角不同,斜率是否相同?
问题2:由例1进一步分析,当直线的倾斜角由0°由逐渐增大到180°,由其斜率如何变化?为什么?
高二年级 | 数学
数学问题解决策略
结合正切函数y=tan x在
的图象
高二年级 | 数学
数学问题解决策略
高二年级 | 数学
数学结论
设直线的倾斜角为α,斜率为k.
α的大小 0° 0°<α<90° 90° 90°<α<180°
k的范围 k=0 k>0 不存在 k<0
k的增减性 随α的增大而增大 随α的增大而增大
高二年级 | 数学
数学结论
设直线的倾斜角为α,斜率为k.
结论拓展:
(1)当倾斜角为90°时,即x1=x2时,直线的斜率不存在,.
(2)斜率公式中k的值与P1,P2两点在该直线上的位置无关.
(3)斜率公式中两纵坐标和两横坐标在公式中的次序可以同时调换.
(4)若直线与x轴平行或重合,则k=0.
高二年级 | 数学
例题演练
已知两点A(-3,4),B(3,2),过点P(1,0)的
直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
要使l与线段AB有公共点,
则直线l的斜率k的取值范围是
(-∞,-1]∪[1,+∞).
高二年级 | 数学
例题演练
(2)求直线l的倾斜角α的取值范围.
解 由题意可知直线l的倾斜角介于直线
PB与PA的倾斜角之间,又PB的倾斜角是45°
PA的倾斜角是135°
所以α的取值范围是45°≤α≤135°.
高二年级 | 数学
课堂小结
1.知识清单:
(1)直线的倾斜角及其范围.
(2)直线斜率的定义和斜率公式.
2.方法归纳:数形结合思想.
3.常见误区:忽视倾斜角范围,图形理解不清.
谢谢观看
高二年级 | 数学
《直线的倾斜角与斜率》
《直线的倾斜角与斜率》
年 级:高二年级
学 科:数学(人教版)
主讲人:田方舒
学 校:湖南省株洲市渌口区第三中学
高二年级 | 数学
导语
学生自学章引言的内容
问题1:在平面直角坐标系中,表示点用什么表示?直线用什么表示?
下面,我们从研究直线的倾斜角和斜率开 始探究解析几何的世界.
点——坐标
直线——方程
问题2:如何用坐标表示直线呢?
高二年级 | 数学
数学问题引入(一)
问题1:在平面几何中,确定直线的条件是什么?对于平面直角坐标系内的一条直线,它的位置由哪些条件确定?
问题2:在平面直角坐标系内给一个点,过这个点有无数条直线。
再给一个什么条件就可以唯一确定一条直线呢?
请学生手动操作体验
高二年级 | 数学
数学概念
一般地,我们以水平线x轴为基准,这也符合我们日常表示物体倾斜程度的习惯。因此我们约定图1中的角表示直线的倾斜程度,把它就叫倾斜角。
高二年级 | 数学
数学概念
当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角。
高二年级 | 数学
数学概念
直线l 倾斜角为锐角,直线l’的倾斜角为钝角。当直线l与x轴平行或重合时,规定它的倾斜角为0°.
高二年级 | 数学
数学问题
追问:依倾斜角的定义,倾斜角的范围是什么?
高二年级 | 数学
数学概念
倾斜角的几何意义:
(1)从运动变化的观点来看,当直线l与x轴相交时,直线l的倾斜角是由x轴绕直线l与x轴的交点按逆时针方向旋转到与直线l重合时所得到的最小正角.
(2)倾斜角从“形”的方面直观地体现了直线对x轴正向的倾斜程度.
直线的倾斜角α的取值范围:0°≤α<180°。
高二年级 | 数学
数学概念问题剖析
练习:判断下列直线的倾斜角是否正确?
高二年级 | 数学
数学情景引入(二)
交通工程上一般用“坡度”来描述一段道路对于水平
方向的倾斜程度,如图,一辆汽车沿某条道路从A点
前进到B点,在水平方向前进的距离为AD,竖直方
向上升的高度为DB(如果是下降,则DB的值为负实数),
则坡度k= 若k>0,则表示上坡,若k<0,
则表示下坡,为了实际应用与安全,在道路铺设时常
要规划坡度的大小.那么“坡度”是如何来刻画道路
的倾斜程度的呢?
高二年级 | 数学
数学问题探究
问题1:将此图形抽象到坐标系中,(利用几何画板给出图形),演示出一条直线l与x轴的交点A相对固定,直线上另一点B在直线上运动,观察坡度情况?如果B点固定A点在x轴上运动,观察坡度的变化情况?
高二年级 | 数学
数学概念
把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即
k=tan α.
高二年级 | 数学
数学问题引入(三)
由于两点可以确定一条直线,那么我们直线上任取两点P1(x1,y1),P2(x2,y2),x1≠x2,可知直线l由P1,P2唯一确定。所以,可以推断,直线l的倾斜角一定与P1,P2两点的坐标有内在联系的。
高二年级 | 数学
数学问题探究
问题1:在平面直角坐标系中,设直线l的倾斜角为α.(教材52页问题探究)
(1)已知直线l 经过O(0,0),P( ,1),α与O,P的坐标有什么关系?
高二年级 | 数学
数学问题探究
问题1:在平面直角坐标系中,设直线l的倾斜角为α.(教材52页问题探究)
(2)类似地,如果直线l经过P1(-1,1),P2( ,0),α与P1,P2的坐标有什么关系?
高二年级 | 数学
数学问题探究
问题1:在平面直角坐标系中,设直线l的倾斜角为α.(教材52页问题探究)
(3)一般地,如果直线l经过两点P1(x1,y1),P2(x2,y2),x1≠x2,那么α与P1,P2的坐标有什么关系?
高二年级 | 数学
数学公式
如果直线l经过两点P1(x1,y1),P2(x2,y2),x1≠x2,可得斜率公式:
高二年级 | 数学
知识拓展
直线P1P2上的向量 以及与它平行的非零
向量都是直线的方向向量。直线P1P2的方向向
量 的坐标为(x2-x1,y2-y1)直线P1P2与x轴
不垂直时,x1≠x2.此时向量 也是直
线P1P2的方向向量,且它的坐标为
,
其中k是直线P1P2的斜率.
高二年级 | 数学
知识拓展
若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则
高二年级 | 数学
例题解析
例1: 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角?
高二年级 | 数学
例题解析
解析:
解析:由kAB>0,kCA>0可知,
直线AB与CA的 倾斜角为锐角,kBC<0,直线BC倾斜角为钝角。
高二年级 | 数学
数学问题引入(四)
问题1:是否每条直线都有斜率?倾斜角不同,斜率是否相同?
问题2:由例1进一步分析,当直线的倾斜角由0°由逐渐增大到180°,由其斜率如何变化?为什么?
高二年级 | 数学
数学问题解决策略
结合正切函数y=tan x在
的图象
高二年级 | 数学
数学问题解决策略
高二年级 | 数学
数学结论
设直线的倾斜角为α,斜率为k.
α的大小 0° 0°<α<90° 90° 90°<α<180°
k的范围 k=0 k>0 不存在 k<0
k的增减性 随α的增大而增大 随α的增大而增大
高二年级 | 数学
数学结论
设直线的倾斜角为α,斜率为k.
结论拓展:
(1)当倾斜角为90°时,即x1=x2时,直线的斜率不存在,.
(2)斜率公式中k的值与P1,P2两点在该直线上的位置无关.
(3)斜率公式中两纵坐标和两横坐标在公式中的次序可以同时调换.
(4)若直线与x轴平行或重合,则k=0.
高二年级 | 数学
例题演练
已知两点A(-3,4),B(3,2),过点P(1,0)的
直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
要使l与线段AB有公共点,
则直线l的斜率k的取值范围是
(-∞,-1]∪[1,+∞).
高二年级 | 数学
例题演练
(2)求直线l的倾斜角α的取值范围.
解 由题意可知直线l的倾斜角介于直线
PB与PA的倾斜角之间,又PB的倾斜角是45°
PA的倾斜角是135°
所以α的取值范围是45°≤α≤135°.
高二年级 | 数学
课堂小结
1.知识清单:
(1)直线的倾斜角及其范围.
(2)直线斜率的定义和斜率公式.
2.方法归纳:数形结合思想.
3.常见误区:忽视倾斜角范围,图形理解不清.
谢谢观看
高二年级 | 数学
