人教版数学八年级下册18.1.1 平行四边形的性质 第一课时 课件(共13张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.1.1 平行四边形的性质 第一课时 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 23:34:54 | ||
图片预览

文档简介
(共13张PPT)
18.1.1 平行四边形的性质
(第一课时)
人教版初中数学八年级下册第18章平行四边形
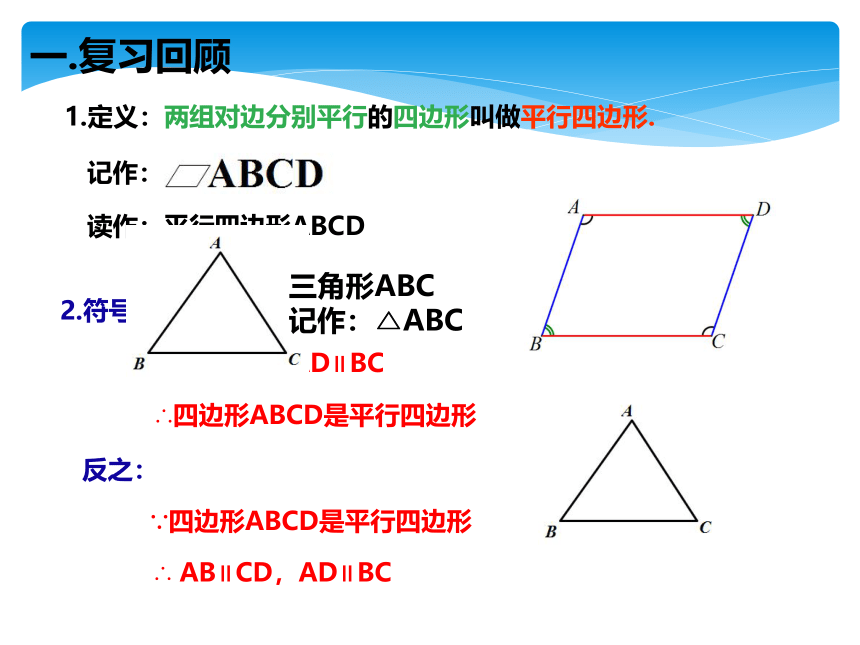
1.定义:两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
2.符号语言表示:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
一.复习回顾
反之:
∴ AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
三角形ABC
记作:△ABC
记作:
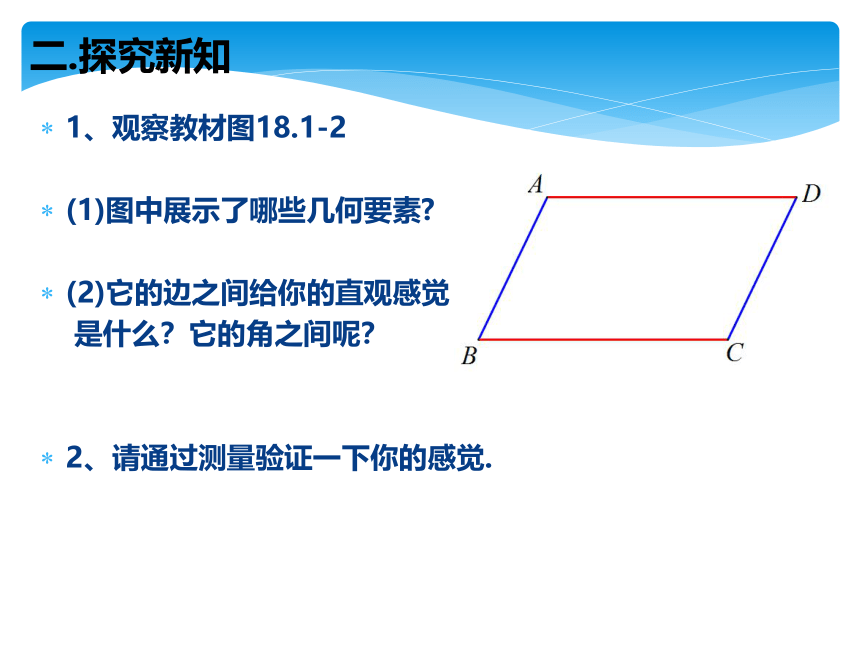
1、观察教材图18.1-2
(1)图中展示了哪些几何要素
(2)它的边之间给你的直观感觉
是什么?它的角之间呢?
2、请通过测量验证一下你的感觉.
二.探究新知
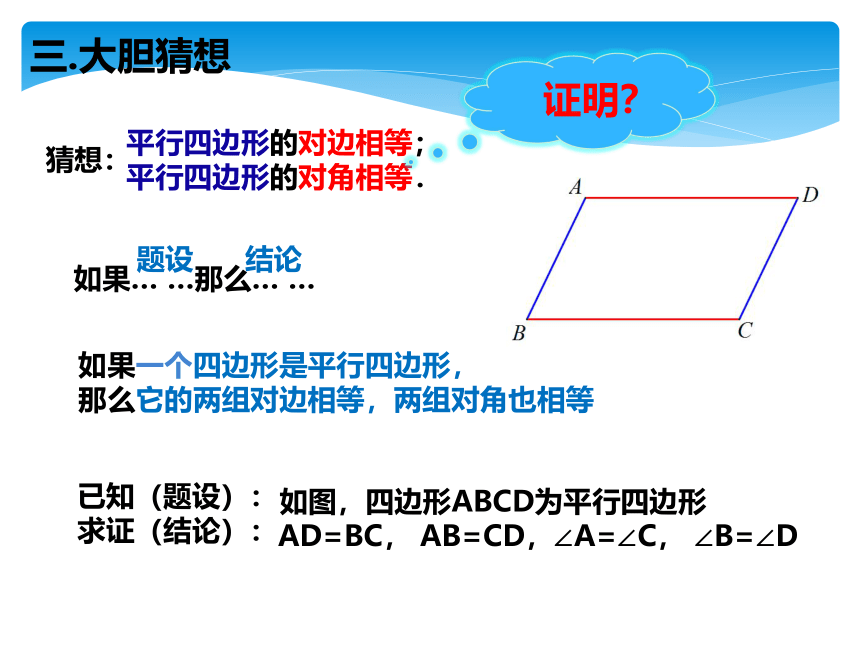
三.大胆猜想
平行四边形的对边相等;
平行四边形的对角相等.
证明?
已知(题设):
求证(结论):
如果… …那么… …
题设 结论
如图,四边形ABCD为平行四边形
AD=BC, AB=CD,∠A=∠C, ∠B=∠D
如果一个四边形是平行四边形,
那么它的两组对边相等,两组对角也相等
猜想:
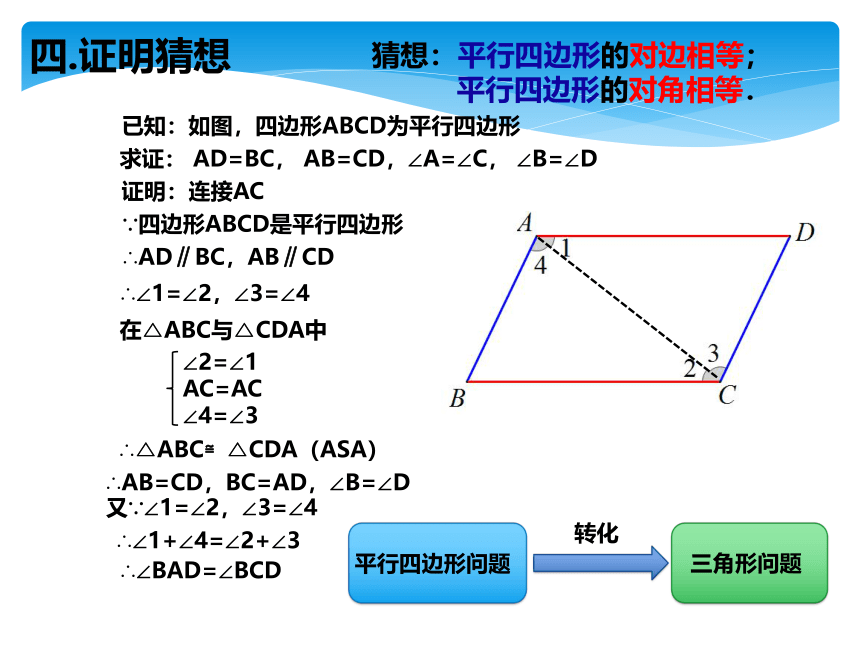
四.证明猜想
猜想:平行四边形的对边相等;
平行四边形的对角相等.
已知:如图,四边形ABCD为平行四边形
求证: AD=BC, AB=CD,∠A=∠C, ∠B=∠D
证明:连接AC
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD
在△ABC与△CDA中
∴AB=CD,BC=AD,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
∴△ABC≌△CDA(ASA)
∴∠1=∠2,∠3=∠4
∴∠BAD=∠BCD
∠2=∠1
AC=AC
∠4=∠3
平行四边形问题
三角形问题
转化
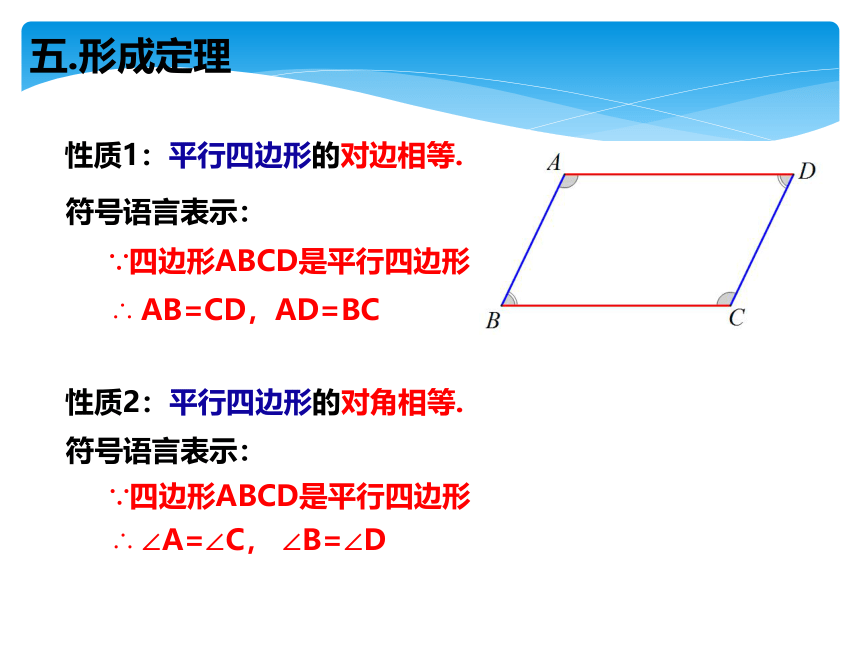
五.形成定理
性质1:平行四边形的对边相等.
∴ ∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形
符号语言表示:
性质2:平行四边形的对角相等.
∴ AB=CD,AD=BC
∵四边形ABCD是平行四边形
符号语言表示:
1.如图, ABCD中,AB=12,BC=15,∠B=60°,
(1)CD= ,AD = ,
(2)∠A = ,∠C = ,∠D = .
六.应用新知
12
15
120°
120°
60°
2. 如图, ABCD中,DE⊥AB,BF⊥CD,垂
足分别为E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形
∴∠AED=∠CFB=900
∴△ADE≌△CBF(AAS)
∴∠A=∠C,AD=CB
∴AE=CF
又∵DE⊥AB,BF⊥CD
∴在△ADE与△CBF中
∠AED=∠CFB
∠A=∠C
AD=CB
七.综合应用
如图, a∥b, c∥d, c,d与a,b 分别相交于A、B、C、D四点,那么AB与CD具有怎样的数量关系?
解 ∵a∥b, c∥d
∴四边形ABCD是平行四边形
∴AB=CD
两条平行线之间的任何两条平行线段都相等.
变式:如果将c∥d 改为 c⊥ b ,d⊥ b 呢?
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
八.平行线间的距离
两条平行线中,一条直线上任意一点到另一条
直线的距离,叫做这两条平行线之间的距离.
如图,a∥b,A是a上的任意一点,AB⊥b,B是垂足,线段
AB的长就是a,b之间的距离.
平行线间的距离
思考:
如图,直线a∥b,△ABC与△DBC的面积相等吗?
(1)本节课我们学习了哪些知识?
(2)通过本节的学习,你认为对一个几何图形的研究
通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?
九. 小结及作业
作业:教科书第43页练习第1,2题;
习题18.1第1,2题.
小结:
18.1.1 平行四边形的性质
(第一课时)
人教版初中数学八年级下册第18章平行四边形
1.定义:两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
2.符号语言表示:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
一.复习回顾
反之:
∴ AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
三角形ABC
记作:△ABC
记作:
1、观察教材图18.1-2
(1)图中展示了哪些几何要素
(2)它的边之间给你的直观感觉
是什么?它的角之间呢?
2、请通过测量验证一下你的感觉.
二.探究新知
三.大胆猜想
平行四边形的对边相等;
平行四边形的对角相等.
证明?
已知(题设):
求证(结论):
如果… …那么… …
题设 结论
如图,四边形ABCD为平行四边形
AD=BC, AB=CD,∠A=∠C, ∠B=∠D
如果一个四边形是平行四边形,
那么它的两组对边相等,两组对角也相等
猜想:
四.证明猜想
猜想:平行四边形的对边相等;
平行四边形的对角相等.
已知:如图,四边形ABCD为平行四边形
求证: AD=BC, AB=CD,∠A=∠C, ∠B=∠D
证明:连接AC
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD
在△ABC与△CDA中
∴AB=CD,BC=AD,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
∴△ABC≌△CDA(ASA)
∴∠1=∠2,∠3=∠4
∴∠BAD=∠BCD
∠2=∠1
AC=AC
∠4=∠3
平行四边形问题
三角形问题
转化
五.形成定理
性质1:平行四边形的对边相等.
∴ ∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形
符号语言表示:
性质2:平行四边形的对角相等.
∴ AB=CD,AD=BC
∵四边形ABCD是平行四边形
符号语言表示:
1.如图, ABCD中,AB=12,BC=15,∠B=60°,
(1)CD= ,AD = ,
(2)∠A = ,∠C = ,∠D = .
六.应用新知
12
15
120°
120°
60°
2. 如图, ABCD中,DE⊥AB,BF⊥CD,垂
足分别为E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形
∴∠AED=∠CFB=900
∴△ADE≌△CBF(AAS)
∴∠A=∠C,AD=CB
∴AE=CF
又∵DE⊥AB,BF⊥CD
∴在△ADE与△CBF中
∠AED=∠CFB
∠A=∠C
AD=CB
七.综合应用
如图, a∥b, c∥d, c,d与a,b 分别相交于A、B、C、D四点,那么AB与CD具有怎样的数量关系?
解 ∵a∥b, c∥d
∴四边形ABCD是平行四边形
∴AB=CD
两条平行线之间的任何两条平行线段都相等.
变式:如果将c∥d 改为 c⊥ b ,d⊥ b 呢?
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
八.平行线间的距离
两条平行线中,一条直线上任意一点到另一条
直线的距离,叫做这两条平行线之间的距离.
如图,a∥b,A是a上的任意一点,AB⊥b,B是垂足,线段
AB的长就是a,b之间的距离.
平行线间的距离
思考:
如图,直线a∥b,△ABC与△DBC的面积相等吗?
(1)本节课我们学习了哪些知识?
(2)通过本节的学习,你认为对一个几何图形的研究
通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?
九. 小结及作业
作业:教科书第43页练习第1,2题;
习题18.1第1,2题.
小结:
