人教版数学八年级下册18.1.1 平行四边形的性质-课件(共13张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.1.1 平行四边形的性质-课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 08:51:04 | ||
图片预览


文档简介
(共13张PPT)
18.1.1平行四边形的性质
人教版—八年级—下册—数学
欣赏
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四
边形的定义吗?
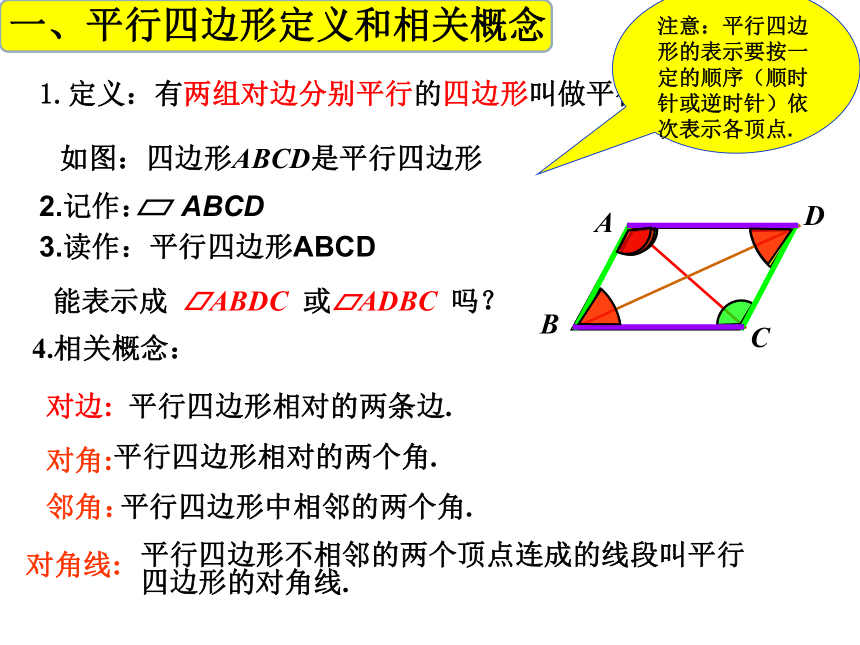
1.定义:有两组对边分别平行的四边形叫做平行四边形.
A
D
C
B
如图:四边形ABCD是平行四边形
ABDC
ADBC
能表示成 或 吗?
注意:平行四边形的表示要按一定的顺序(顺时针或逆时针)依次表示各顶点.
对边:
对角:
平行四边形相对的两个角.
平行四边形相对的两条边.
一、平行四边形定义和相关概念
2.记作: ABCD
3.读作:平行四边形ABCD
4.相关概念:
平行四边形不相邻的两个顶点连成的线段叫平行
四边形的对角线.
对角线:
邻角:
平行四边形中相邻的两个角.
A
B
C
D
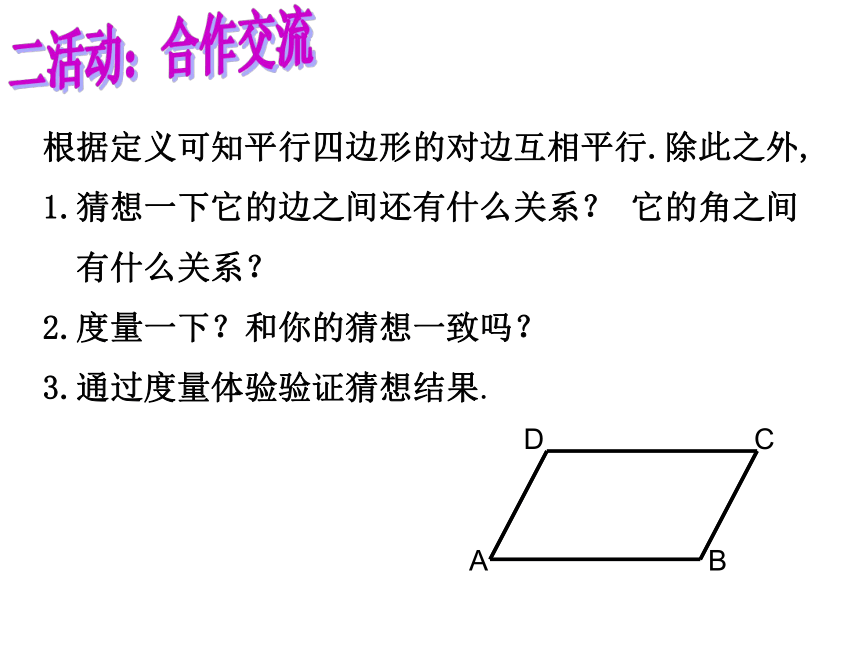
根据定义可知平行四边形的对边互相平行.除此之外,
1.猜想一下它的边之间还有什么关系? 它的角之间
有什么关系?
2.度量一下?和你的猜想一致吗?
3.通过度量体验验证猜想结果.
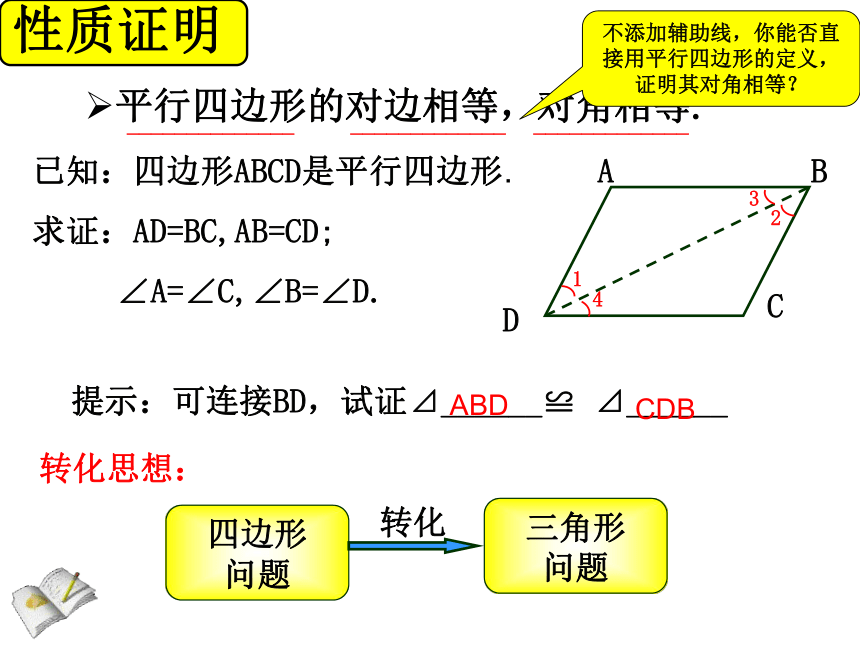
性质证明
平行四边形的对边相等,对角相等.
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD;
∠A=∠C,∠B=∠D.
D
C
B
A
提示:可连接BD,试证⊿______≌ ⊿______
转化思想:
四边形
问题
三角形
问题
转化
ABD
CDB
______________
_____________
_____________
不添加辅助线,你能否直接用平行四边形的定义,证明其对角相等?
4
1
2
3
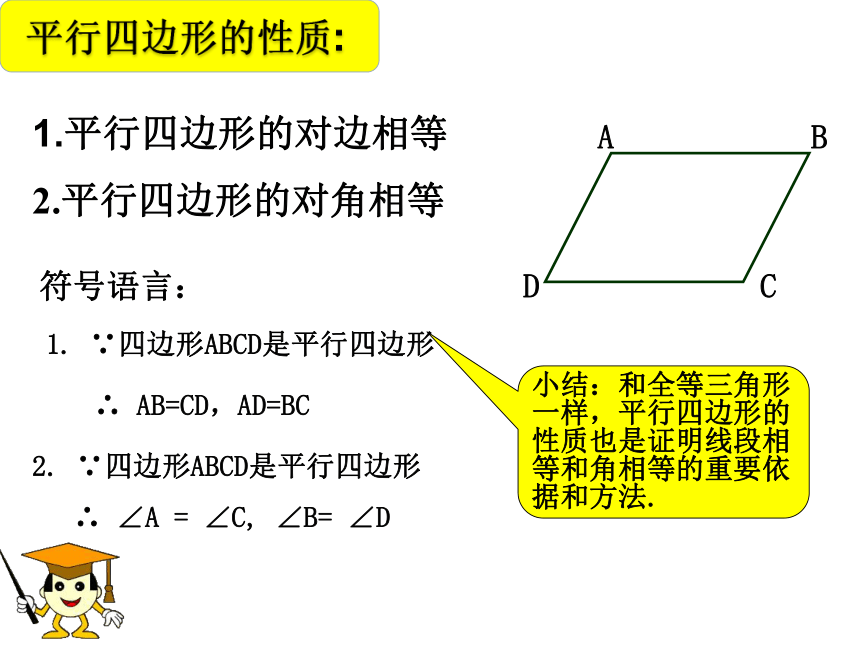
1.平行四边形的对边相等
1. ∵四边形ABCD是平行四边形
2. ∵四边形ABCD是平行四边形
小结:和全等三角形
一样,平行四边形的
性质也是证明线段相
等和角相等的重要依
据和方法.
∴ AB=CD,AD=BC
∴ ∠A = ∠C, ∠B= ∠D
2.平行四边形的对角相等
平行四边形的性质:
D
C
B
A
符号语言:
学以致用:
如图,剪两张对边平行的纸条,随意交叉叠放
在一起重合的部分构成了一个四边形,转动其中
一张纸条,线段AD和BC的长度有什么关系 为什么
相等
练习:如图,在
1.若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______.
ABCD中,
2.若∠A+ ∠C= 200°,则∠A=______ 、∠B=______.
C
D
A
B
50°
130°
50°
100°
80°
性质应用
已知平行四边形的一个内角可求其它各内角
性质应用
3.若AB=1㎝,BC=2 ㎝
,则
ABCD的周长=______
6cm
4.若AB=4㎝, BC=______
ABCD的周长为18㎝,
5cm
平行四边形的周长等于两邻边之和×2
例1 如图, ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
典例精析
练习: 如图, ABCD中,E,F是对角线AC上两点并且AE=CF .求证:BE=DF.
A
B
C
D
E
F
小试牛刀:
学校买了四棵树,准备栽在花园里,已经栽了三棵树,(如图)现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里
拓展题
A
C
B
D1
D2
D3
1.定义:
2.性质:
3.转化思想:
课堂小结
C
D
A
B
AB∥CD
AD∥BC
四边形ABCD是平行四边形
四边形问题
三角形问题
转化
对边平行且相等
四边形ABCD是平行四边形
对角相等 邻角互补
通过本节课的学习,你有什么收获?
作业:小练“平行四边形的性质”
要求: C组做基础练习;B组做基础+综合练习;A组基础+综合+创新应用.
谢谢!
18.1.1平行四边形的性质
人教版—八年级—下册—数学
欣赏
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四
边形的定义吗?
1.定义:有两组对边分别平行的四边形叫做平行四边形.
A
D
C
B
如图:四边形ABCD是平行四边形
ABDC
ADBC
能表示成 或 吗?
注意:平行四边形的表示要按一定的顺序(顺时针或逆时针)依次表示各顶点.
对边:
对角:
平行四边形相对的两个角.
平行四边形相对的两条边.
一、平行四边形定义和相关概念
2.记作: ABCD
3.读作:平行四边形ABCD
4.相关概念:
平行四边形不相邻的两个顶点连成的线段叫平行
四边形的对角线.
对角线:
邻角:
平行四边形中相邻的两个角.
A
B
C
D
根据定义可知平行四边形的对边互相平行.除此之外,
1.猜想一下它的边之间还有什么关系? 它的角之间
有什么关系?
2.度量一下?和你的猜想一致吗?
3.通过度量体验验证猜想结果.
性质证明
平行四边形的对边相等,对角相等.
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD;
∠A=∠C,∠B=∠D.
D
C
B
A
提示:可连接BD,试证⊿______≌ ⊿______
转化思想:
四边形
问题
三角形
问题
转化
ABD
CDB
______________
_____________
_____________
不添加辅助线,你能否直接用平行四边形的定义,证明其对角相等?
4
1
2
3
1.平行四边形的对边相等
1. ∵四边形ABCD是平行四边形
2. ∵四边形ABCD是平行四边形
小结:和全等三角形
一样,平行四边形的
性质也是证明线段相
等和角相等的重要依
据和方法.
∴ AB=CD,AD=BC
∴ ∠A = ∠C, ∠B= ∠D
2.平行四边形的对角相等
平行四边形的性质:
D
C
B
A
符号语言:
学以致用:
如图,剪两张对边平行的纸条,随意交叉叠放
在一起重合的部分构成了一个四边形,转动其中
一张纸条,线段AD和BC的长度有什么关系 为什么
相等
练习:如图,在
1.若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______.
ABCD中,
2.若∠A+ ∠C= 200°,则∠A=______ 、∠B=______.
C
D
A
B
50°
130°
50°
100°
80°
性质应用
已知平行四边形的一个内角可求其它各内角
性质应用
3.若AB=1㎝,BC=2 ㎝
,则
ABCD的周长=______
6cm
4.若AB=4㎝, BC=______
ABCD的周长为18㎝,
5cm
平行四边形的周长等于两邻边之和×2
例1 如图, ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
典例精析
练习: 如图, ABCD中,E,F是对角线AC上两点并且AE=CF .求证:BE=DF.
A
B
C
D
E
F
小试牛刀:
学校买了四棵树,准备栽在花园里,已经栽了三棵树,(如图)现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里
拓展题
A
C
B
D1
D2
D3
1.定义:
2.性质:
3.转化思想:
课堂小结
C
D
A
B
AB∥CD
AD∥BC
四边形ABCD是平行四边形
四边形问题
三角形问题
转化
对边平行且相等
四边形ABCD是平行四边形
对角相等 邻角互补
通过本节课的学习,你有什么收获?
作业:小练“平行四边形的性质”
要求: C组做基础练习;B组做基础+综合练习;A组基础+综合+创新应用.
谢谢!
