人教版数学八年级下册18.2.1矩形-矩形的判定 -课件(共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.1矩形-矩形的判定 -课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 08:56:02 | ||
图片预览




文档简介
(共15张PPT)
特殊的平行四边形
——矩形的判定
01
复习引入
1、矩形的定义:
2、矩形的性质:
有一个角是直角的平行四边形是矩形.
(1)具有平行四边形的所有性质
(2)矩形的四个角都是直角
(3)矩形的对角线相等
02
归纳判定
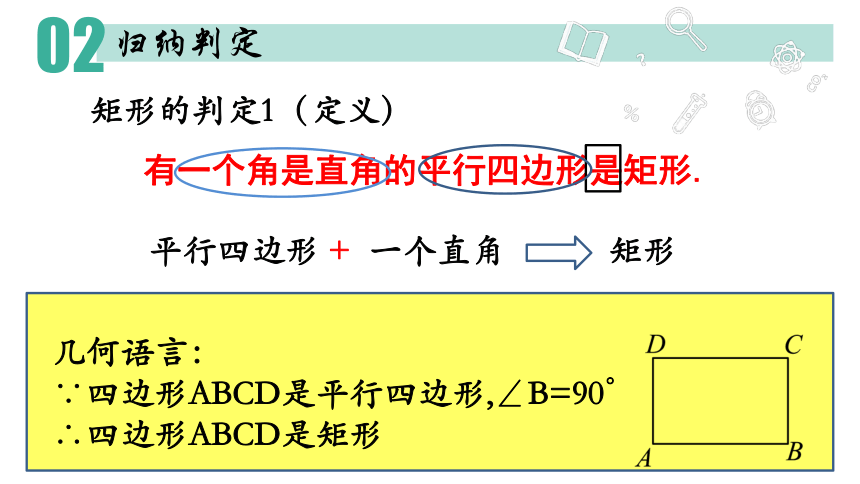
有一个角是直角的平行四边形是矩形.
平行四边形 + 一个直角 矩形
矩形的判定1(定义)
几何语言:
∵四边形ABCD是平行四边形,∠B=90°
∴四边形ABCD是矩形
02
思维延伸
【思考】能否改变平行四边形的其他元素,使它变成矩形?
猜想:对角线相等的平行四边形是矩形
02
证明猜想
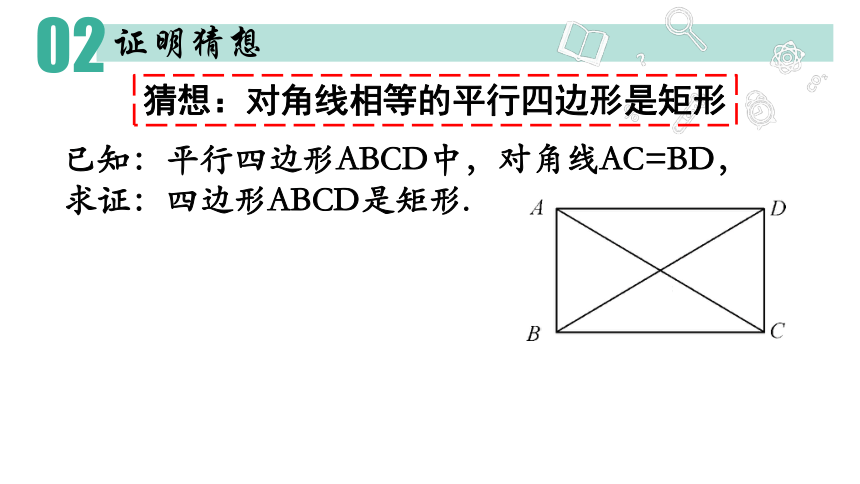
猜想:对角线相等的平行四边形是矩形
已知:平行四边形ABCD中,对角线AC=BD,
求证:四边形ABCD是矩形.
02
归纳判定
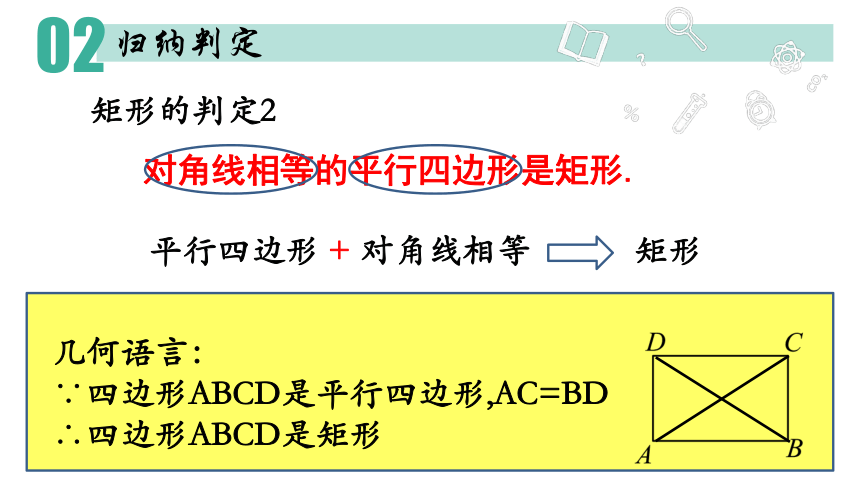
对角线相等的平行四边形是矩形.
平行四边形 + 对角线相等 矩形
矩形的判定2
几何语言:
∵四边形ABCD是平行四边形,AC=BD
∴四边形ABCD是矩形
02
活动探究
【思考】若题目中给出的是四边形的条件,而不是平行四边形,如何证明矩形?
【探究】分别画出下列图形,小组交流,你发现了什么?
图1:画一个四边形,只有一个角是直角
图2:画一个四边形,只有两个角是直角
图3:画一个四边形,只有三个角是直角
猜想:有三个角是直角的四边形是矩形
02
证明猜想
猜想:有三个角是直角的四边形是矩形
已知:四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形.
02
归纳判定
有三个角是直角的四边形是矩形.
任意四边形 + 三个角是直角 矩形
矩形的判定3
几何语言:
∵四边形ABCD中, ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
03
基础练习
基础巩固
1.下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形.( )
(3)对角线相等的四边形是矩形.( )
(4)对角线互相平分,且有一个角是直角的四边形是矩形. ( )
×
√
×
√
03
例题解析
【例】如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
03
练习巩固
1.如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,求证:四边形ADBE是矩形.
03
练习巩固
【练习】如图,MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.求证:四边形ABCD是矩形.
04
有三个角是直角的四边形是矩形
对角线相等的平行四边形是矩形
一个角是直角的平行四边形是矩形
矩形判定
小结思考
THANK YOU!
特殊的平行四边形
——矩形的判定
01
复习引入
1、矩形的定义:
2、矩形的性质:
有一个角是直角的平行四边形是矩形.
(1)具有平行四边形的所有性质
(2)矩形的四个角都是直角
(3)矩形的对角线相等
02
归纳判定
有一个角是直角的平行四边形是矩形.
平行四边形 + 一个直角 矩形
矩形的判定1(定义)
几何语言:
∵四边形ABCD是平行四边形,∠B=90°
∴四边形ABCD是矩形
02
思维延伸
【思考】能否改变平行四边形的其他元素,使它变成矩形?
猜想:对角线相等的平行四边形是矩形
02
证明猜想
猜想:对角线相等的平行四边形是矩形
已知:平行四边形ABCD中,对角线AC=BD,
求证:四边形ABCD是矩形.
02
归纳判定
对角线相等的平行四边形是矩形.
平行四边形 + 对角线相等 矩形
矩形的判定2
几何语言:
∵四边形ABCD是平行四边形,AC=BD
∴四边形ABCD是矩形
02
活动探究
【思考】若题目中给出的是四边形的条件,而不是平行四边形,如何证明矩形?
【探究】分别画出下列图形,小组交流,你发现了什么?
图1:画一个四边形,只有一个角是直角
图2:画一个四边形,只有两个角是直角
图3:画一个四边形,只有三个角是直角
猜想:有三个角是直角的四边形是矩形
02
证明猜想
猜想:有三个角是直角的四边形是矩形
已知:四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形.
02
归纳判定
有三个角是直角的四边形是矩形.
任意四边形 + 三个角是直角 矩形
矩形的判定3
几何语言:
∵四边形ABCD中, ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
03
基础练习
基础巩固
1.下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形.( )
(3)对角线相等的四边形是矩形.( )
(4)对角线互相平分,且有一个角是直角的四边形是矩形. ( )
×
√
×
√
03
例题解析
【例】如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
03
练习巩固
1.如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,求证:四边形ADBE是矩形.
03
练习巩固
【练习】如图,MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.求证:四边形ABCD是矩形.
04
有三个角是直角的四边形是矩形
对角线相等的平行四边形是矩形
一个角是直角的平行四边形是矩形
矩形判定
小结思考
THANK YOU!
