7.3解决问题的策略的整理与练习导学案(含答案)五年级数学下册-苏教版
文档属性
| 名称 | 7.3解决问题的策略的整理与练习导学案(含答案)五年级数学下册-苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 133.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 17:31:14 | ||
图片预览

文档简介
7.3解决问题的策略的整理与练习
知识梳理
填空:
1、解决问题时,可以把没有学过的新问题转化成( )的问题。
2、解决问题时,把复杂的问题转化为( )的问题。
3、解决问题时,有时( )可以帮助我们找到转化的方法。
二、题型、方法归纳与典例精讲
1、用分数的基本性质进行转化。
例: 填空:
用“转化”的测略解决图形问题
例: 计算下面图形的周长。
3、用“转化”的测略解决问题。
例:明光小学有一个花坛(如下图)。图中正方形的边长为10米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。这个花坛的面积是多少平方米?
三、随堂检测
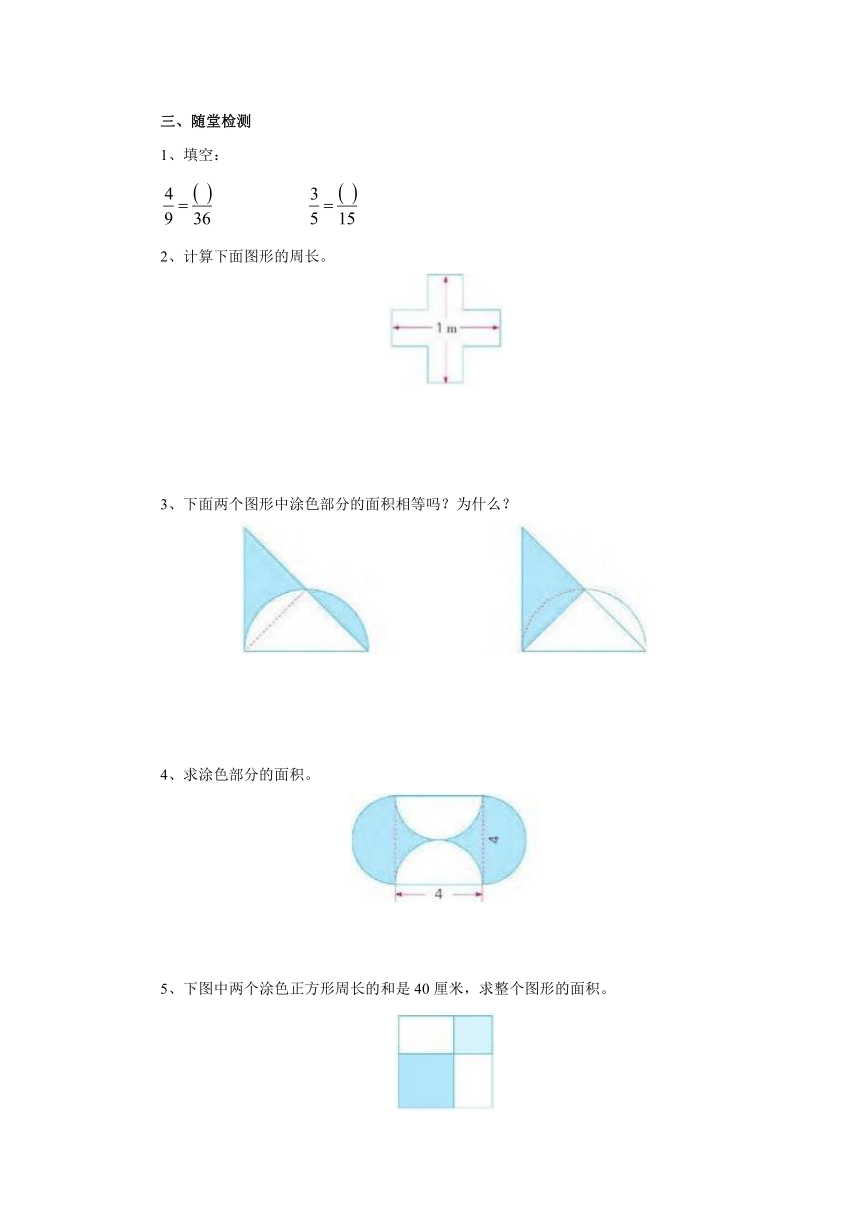
1、填空:
计算下面图形的周长。
下面两个图形中涂色部分的面积相等吗?为什么?
求涂色部分的面积。
5、下图中两个涂色正方形周长的和是40厘米,求整个图形的面积。
参考答案
知识梳理
1、熟悉
2、简单
3、画图
题型、方法归纳与典例精讲
1、15 25
2、3.14×4+3.14×4×2÷2
=12.56+12.56
=25.12(厘米)
答:图形的周长是25.12厘米
3、3.14×32×3+10×10
=84.78+100
=184.78(平方厘米)
答:这个花坛的面积是184.78平方米。
随堂检测
1、16 9
2、1×4=4(米)
答:这个图形的周长是4米。
相等
4×4=16(平方厘米)
答:涂色部分的面积是16平方厘米。
(40÷4)×(40÷4)=100(平方厘米)
答:整个图形的面积100平方厘米。
知识梳理
填空:
1、解决问题时,可以把没有学过的新问题转化成( )的问题。
2、解决问题时,把复杂的问题转化为( )的问题。
3、解决问题时,有时( )可以帮助我们找到转化的方法。
二、题型、方法归纳与典例精讲
1、用分数的基本性质进行转化。
例: 填空:
用“转化”的测略解决图形问题
例: 计算下面图形的周长。
3、用“转化”的测略解决问题。
例:明光小学有一个花坛(如下图)。图中正方形的边长为10米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。这个花坛的面积是多少平方米?
三、随堂检测
1、填空:
计算下面图形的周长。
下面两个图形中涂色部分的面积相等吗?为什么?
求涂色部分的面积。
5、下图中两个涂色正方形周长的和是40厘米,求整个图形的面积。
参考答案
知识梳理
1、熟悉
2、简单
3、画图
题型、方法归纳与典例精讲
1、15 25
2、3.14×4+3.14×4×2÷2
=12.56+12.56
=25.12(厘米)
答:图形的周长是25.12厘米
3、3.14×32×3+10×10
=84.78+100
=184.78(平方厘米)
答:这个花坛的面积是184.78平方米。
随堂检测
1、16 9
2、1×4=4(米)
答:这个图形的周长是4米。
相等
4×4=16(平方厘米)
答:涂色部分的面积是16平方厘米。
(40÷4)×(40÷4)=100(平方厘米)
答:整个图形的面积100平方厘米。
