2023年高三化学二轮专题复习 晶体结构与性质 课件 (共46张PPT)
文档属性
| 名称 | 2023年高三化学二轮专题复习 晶体结构与性质 课件 (共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 22.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-04-22 10:01:47 | ||
图片预览











文档简介
(共46张PPT)
晶体结构与性质
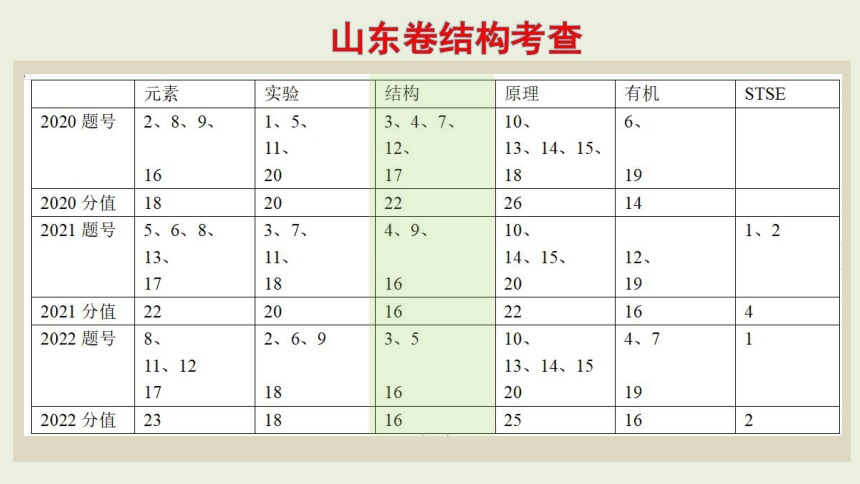
山东卷结构考查
考点一
晶体类型的判断
熔沸点变化规律
注重强化:
准确把握基础知识、基本规律,落实高考必备知识。
一、晶体的重要性质——晶体熔、沸点
1.比较晶体熔、沸点高低的规律方法
(1)不同类型晶体的熔、沸点高低一般规律:
共价晶体>离子晶体>分子晶体。
金属晶体的熔、沸点差别很大:如钨、铂等熔点很高,汞、铯等熔点很低。
【回归基础】
(2)相同类型晶体熔、沸点高低的一般规律
①共价晶体
②离子晶体
(2)相同类型晶体熔、沸点高低的一般规律
①共价晶体
由共价键形成的共价晶体中,原子半径小,键长短,键能大,晶体的熔、沸点高。如熔点:金刚石>碳化硅>硅。
②离子晶体
一般来说,阴、阳离子的电荷数越多,离子半径越小,则离子间的作用力就越强,晶格能就越大,其晶体的熔、沸点就越高。如熔点:MgO>NaCl>CsCl。
③分子晶体
④金属晶体
③分子晶体
a.分子间作用力越大,物质的熔、沸点越高;具有氢键的分子晶体熔、沸点反常地高。如H2O>H2Te>H2Se>H2S。
b.组成和结构相似的分子晶体,相对分子质量越大,熔、沸点越高。如SnH4>GeH4>SiH4>CH4。
c.组成和结构不相似的分子晶体(相对分子质量接近),分子的极性越大,其熔、沸点越高。如CO>N2。
④金属晶体
金属离子半径越小,离子电荷数越多,金属键越强,金属熔、沸点就越高。如熔、沸点:Al>Mg>Na。
答案:A
考点考法(一) 晶体结构与性质
1.(2022·山东等级考·T5)AlN、GaN属于第三代半导体材料,二者成键结构与金刚石相似,晶体中只存在N—Al键、N—Ga键。下列说法错误的是( )
A.GaN的熔点高于AlN
B.晶体中所有化学键均为极性键
C.晶体中所有原子均采取sp3杂化
D.晶体中所有原子的配位数均相同
高考试题分析
2.(2021·山东等级考·T9)关于CH3OH、N2H4和(CH3)2NNH2的结构与性质,下列说法错误的是( )
A.CH3OH为极性分子
B.N2H4空间结构为平面形
C.N2H4的沸点高于(CH3)2NNH2的
D.CH3OH和(CH3)2NNH2中C、O、N杂化方式均相同
高考试题分析
答案:B
3.(1)研究发现,CO2低压合成甲醇反应为CO2+3H2==
CH3OH+H2O,该反应涉及的4种物质中,沸点从高到低的顺序为 ,原因
______________________。
(2)CaF2、CaCl2晶体的熔点依次为1402 ℃、782 ℃,二者熔点相差较大的主要原因是______________________________________________ ____ ______________________。
H2O>CH3OH>CO2>H2
H2O与CH3OH均为极性分子,H2O中分子间氢键比甲醇多;CO2与H2均为非极性分子,CO2的相对分子质量较大、范德华力较大。
答案:(2)CaF2、CaCl2都是离子晶体,F-的半径小于Cl-,故CaF2的晶格能较大,离子键较强
高考试题分析
考点二
晶胞的分析及计算
角度一
分析晶胞信息确定
化学式、配位数
注重提升:
获取信息能力、逻辑推理能力、
数形结合能力、模型认知能力。
高考试题分析
1.(2022·山东等级考·16)研究笼形包合物结构和性质具有重要意义。化学式为 的笼形包合物四方晶胞结构如图所示(H原子未画出),每个苯环只有一半属于该晶胞。晶胞参数为 。回答下列问题:
(2)晶胞中N原子均参与形成配位键,Ni2+与Zn2+的配位数之比为_____;x∶y∶z=______;晶胞中有d轨道参与杂化的金属离子是______。
答案:2∶3 2∶1∶1 Ni2+ Zn2+
高考试题分析
每个苯环只有一半属于该晶胞
H原子未画出
(4)在水中的溶解度,吡啶远大于苯,主要原因是
① ,② 。
【小问4详解】已知苯分子为非极性分子,吡啶和H2O分子为极性分子,根据相似相溶原理,吡啶易溶于水,且吡啶中N原子上含有孤电子对能与H2O分子形成分子间氢键,从而导致在水中溶解度,吡啶远大于苯。
答案: ①吡啶能与H2O分子形成分子间氢键,②吡啶和H2O均为极性分子,而苯为非极性分子,根据相似相溶原理,吡啶更易溶于水。
高考试题分析
角度二
分析晶胞信息确定
晶胞参数、分数坐标、投影图
注重提升:
获取信息能力、逻辑推理能力、
数形结合能力、模型认知能力。
2.[2020·山东等级考·17(4)]以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子的分数坐标。四方晶系CdSnAs2的晶胞结构如下图所示,晶胞棱边夹角均为90°,晶胞中部分原子的分数坐标如下表所示。
坐标 原子 x y z
Cd 0 0 0
Sn 0 0 0.5
As 0.25 0.25 0.125
高考试题分析
(4)一个晶胞中有 个Sn,找出距离Cd(0,0,0)最近的Sn___________________(用分数坐标表示)。CdSnAs2晶体中与单个Sn键合的As有____个。
4
(0.5,0,0.25)、(0.5,0.5,0)
4
坐标 原子 x y z
Cd 0 0 0
Sn 0 0 0.5
As 0.25 0.25 0.125
高考试题分析
①若晶胞底边的边长均为a pm、高为c pm,阿伏加德罗常数的值为NA,晶体的密度为 g·cm-3(写出表达式)。
高考试题分析
3.[2021·河北卷·17(7)]分别用 、 表示H2PO4-和K+,KH2PO4晶体的四方晶胞如图(a)所示,图(b)、图(c)分别显示的是H2PO4-、K+在晶胞xz面、yz面上的位置:
(2)晶胞在x轴方向的投影图为________(填标号)。
【回归基础】晶胞中原子分数坐标与投影图
1.体心晶胞结构模型的原子分数坐标与投影图
(2)xy平面上的投影图为 。
2.面心立方晶胞结构模型的原子分数坐标和投影图
(2)xy平面上的投影图为 。
金刚石的晶胞图
【思维建模】目标原子分数坐标确定
角度三
分析晶胞信息确定
晶胞密度、微粒间距离、原子空间利用率
注重提升:
获取信息能力、逻辑推理能力、
数形结合能力、模型认知能力。
4.[2022·全国甲卷·35(5)]萤石(CaF2)是自然界中常见的含氟矿物,其晶胞结构如图所示,X代表的离子是
;若该立方晶胞参数为a pm,正负离子的核间距最小为 pm。
高考试题分析
答案:
建构模型
1.晶体密度的计算方法
[2021·山东·16(4)]XeF2晶体属四方晶系,晶胞参数如图所示,晶胞棱边夹角均为90°,该晶胞中有___个XeF2分子。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,
称为原子的分数坐标,如A点原子
的分数坐标为 。已知
Xe—F键长为r pm,则B点原子
的分数坐标为________;晶胞中
A、B间距离d=_______________ pm。
2
高考试题分析
考点考法(二)晶体结构与性质
5.[2021·全国乙卷·35(4)]在金属材料中添加AlCr2颗粒,可以增强材料的耐腐蚀性、硬度和机械性能。AlCr2具有体心四方结构,如图所示。处于顶角位置的是_____原子。设Cr和Al原子半径分别为rCr和rAl,则金属原子空间占有率为________% (列出计算表达式)。
Al
高考试题分析
建构模型
2.晶胞参数的计算方法
堆积模型 简单立方 堆积 体心立方 堆积 六方最密 堆积 面心立方最密堆积
晶胞
配位数 6 8 12 12
【回归基础】常见金属晶体结构分析:原子空间利用率
原子半径(r)和晶胞边长(a)的关系 2r=a 2r= (A2) 2r=a (A3) 2r=
(A1)
一个晶胞内原子数目 1 2 2 4
原子空间利用率 52% 68% 74% 74%
【自主整理】思维建模晶胞相关计算
1.(2022·湖南等级考·节选)钾、铁、硒可以形成一种超导材料,其晶胞在xz、yz和xy平面投影分别如图所示:
(1)该超导材料的最简化学式为________________;
(2)Fe原子的配位数为____________;
(3)该晶胞参数a=b=0.4 nm、c=1.4 nm。阿伏加德罗常数的值为NA,则该晶体的密度为_________g·cm-3(列出计算式)。
当堂巩固提升
2、一种四方结构的超导化合物的晶胞如图1所示。晶胞中Sm和As原子的投影位置如图2所示。
当堂巩固提升
图中F-和O2-共同占据晶胞的上下底面位置,若两者的比例依次用x和1-x代表,则该化合物的化学式表示为______;通过测定密度ρ和晶胞参数,可以计算该物质的x值,完成它们关系表达式:ρ=______g·cm-3。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子分数坐标,例如图1中原子1的坐标为 ,则原子2和3的坐标分别为____、____。
3.某种钛酸钴(CoTiO3)晶胞沿x、y或z轴任意一个方向的投影如图所示。晶胞中Co处于各顶角位置,则O处于
位置,与Co紧邻的O的个数为 。若晶胞中Co与O之间的最短距离为a nm,阿伏加德罗常数的值为NA,该晶体的密度为____________g·cm-3(列出计算式即可)。
1
3
2
4
百尺竿头 更进一步 加油,同学们!
谢谢大家!
晶体结构与性质
山东卷结构考查
考点一
晶体类型的判断
熔沸点变化规律
注重强化:
准确把握基础知识、基本规律,落实高考必备知识。
一、晶体的重要性质——晶体熔、沸点
1.比较晶体熔、沸点高低的规律方法
(1)不同类型晶体的熔、沸点高低一般规律:
共价晶体>离子晶体>分子晶体。
金属晶体的熔、沸点差别很大:如钨、铂等熔点很高,汞、铯等熔点很低。
【回归基础】
(2)相同类型晶体熔、沸点高低的一般规律
①共价晶体
②离子晶体
(2)相同类型晶体熔、沸点高低的一般规律
①共价晶体
由共价键形成的共价晶体中,原子半径小,键长短,键能大,晶体的熔、沸点高。如熔点:金刚石>碳化硅>硅。
②离子晶体
一般来说,阴、阳离子的电荷数越多,离子半径越小,则离子间的作用力就越强,晶格能就越大,其晶体的熔、沸点就越高。如熔点:MgO>NaCl>CsCl。
③分子晶体
④金属晶体
③分子晶体
a.分子间作用力越大,物质的熔、沸点越高;具有氢键的分子晶体熔、沸点反常地高。如H2O>H2Te>H2Se>H2S。
b.组成和结构相似的分子晶体,相对分子质量越大,熔、沸点越高。如SnH4>GeH4>SiH4>CH4。
c.组成和结构不相似的分子晶体(相对分子质量接近),分子的极性越大,其熔、沸点越高。如CO>N2。
④金属晶体
金属离子半径越小,离子电荷数越多,金属键越强,金属熔、沸点就越高。如熔、沸点:Al>Mg>Na。
答案:A
考点考法(一) 晶体结构与性质
1.(2022·山东等级考·T5)AlN、GaN属于第三代半导体材料,二者成键结构与金刚石相似,晶体中只存在N—Al键、N—Ga键。下列说法错误的是( )
A.GaN的熔点高于AlN
B.晶体中所有化学键均为极性键
C.晶体中所有原子均采取sp3杂化
D.晶体中所有原子的配位数均相同
高考试题分析
2.(2021·山东等级考·T9)关于CH3OH、N2H4和(CH3)2NNH2的结构与性质,下列说法错误的是( )
A.CH3OH为极性分子
B.N2H4空间结构为平面形
C.N2H4的沸点高于(CH3)2NNH2的
D.CH3OH和(CH3)2NNH2中C、O、N杂化方式均相同
高考试题分析
答案:B
3.(1)研究发现,CO2低压合成甲醇反应为CO2+3H2==
CH3OH+H2O,该反应涉及的4种物质中,沸点从高到低的顺序为 ,原因
______________________。
(2)CaF2、CaCl2晶体的熔点依次为1402 ℃、782 ℃,二者熔点相差较大的主要原因是______________________________________________ ____ ______________________。
H2O>CH3OH>CO2>H2
H2O与CH3OH均为极性分子,H2O中分子间氢键比甲醇多;CO2与H2均为非极性分子,CO2的相对分子质量较大、范德华力较大。
答案:(2)CaF2、CaCl2都是离子晶体,F-的半径小于Cl-,故CaF2的晶格能较大,离子键较强
高考试题分析
考点二
晶胞的分析及计算
角度一
分析晶胞信息确定
化学式、配位数
注重提升:
获取信息能力、逻辑推理能力、
数形结合能力、模型认知能力。
高考试题分析
1.(2022·山东等级考·16)研究笼形包合物结构和性质具有重要意义。化学式为 的笼形包合物四方晶胞结构如图所示(H原子未画出),每个苯环只有一半属于该晶胞。晶胞参数为 。回答下列问题:
(2)晶胞中N原子均参与形成配位键,Ni2+与Zn2+的配位数之比为_____;x∶y∶z=______;晶胞中有d轨道参与杂化的金属离子是______。
答案:2∶3 2∶1∶1 Ni2+ Zn2+
高考试题分析
每个苯环只有一半属于该晶胞
H原子未画出
(4)在水中的溶解度,吡啶远大于苯,主要原因是
① ,② 。
【小问4详解】已知苯分子为非极性分子,吡啶和H2O分子为极性分子,根据相似相溶原理,吡啶易溶于水,且吡啶中N原子上含有孤电子对能与H2O分子形成分子间氢键,从而导致在水中溶解度,吡啶远大于苯。
答案: ①吡啶能与H2O分子形成分子间氢键,②吡啶和H2O均为极性分子,而苯为非极性分子,根据相似相溶原理,吡啶更易溶于水。
高考试题分析
角度二
分析晶胞信息确定
晶胞参数、分数坐标、投影图
注重提升:
获取信息能力、逻辑推理能力、
数形结合能力、模型认知能力。
2.[2020·山东等级考·17(4)]以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子的分数坐标。四方晶系CdSnAs2的晶胞结构如下图所示,晶胞棱边夹角均为90°,晶胞中部分原子的分数坐标如下表所示。
坐标 原子 x y z
Cd 0 0 0
Sn 0 0 0.5
As 0.25 0.25 0.125
高考试题分析
(4)一个晶胞中有 个Sn,找出距离Cd(0,0,0)最近的Sn___________________(用分数坐标表示)。CdSnAs2晶体中与单个Sn键合的As有____个。
4
(0.5,0,0.25)、(0.5,0.5,0)
4
坐标 原子 x y z
Cd 0 0 0
Sn 0 0 0.5
As 0.25 0.25 0.125
高考试题分析
①若晶胞底边的边长均为a pm、高为c pm,阿伏加德罗常数的值为NA,晶体的密度为 g·cm-3(写出表达式)。
高考试题分析
3.[2021·河北卷·17(7)]分别用 、 表示H2PO4-和K+,KH2PO4晶体的四方晶胞如图(a)所示,图(b)、图(c)分别显示的是H2PO4-、K+在晶胞xz面、yz面上的位置:
(2)晶胞在x轴方向的投影图为________(填标号)。
【回归基础】晶胞中原子分数坐标与投影图
1.体心晶胞结构模型的原子分数坐标与投影图
(2)xy平面上的投影图为 。
2.面心立方晶胞结构模型的原子分数坐标和投影图
(2)xy平面上的投影图为 。
金刚石的晶胞图
【思维建模】目标原子分数坐标确定
角度三
分析晶胞信息确定
晶胞密度、微粒间距离、原子空间利用率
注重提升:
获取信息能力、逻辑推理能力、
数形结合能力、模型认知能力。
4.[2022·全国甲卷·35(5)]萤石(CaF2)是自然界中常见的含氟矿物,其晶胞结构如图所示,X代表的离子是
;若该立方晶胞参数为a pm,正负离子的核间距最小为 pm。
高考试题分析
答案:
建构模型
1.晶体密度的计算方法
[2021·山东·16(4)]XeF2晶体属四方晶系,晶胞参数如图所示,晶胞棱边夹角均为90°,该晶胞中有___个XeF2分子。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,
称为原子的分数坐标,如A点原子
的分数坐标为 。已知
Xe—F键长为r pm,则B点原子
的分数坐标为________;晶胞中
A、B间距离d=_______________ pm。
2
高考试题分析
考点考法(二)晶体结构与性质
5.[2021·全国乙卷·35(4)]在金属材料中添加AlCr2颗粒,可以增强材料的耐腐蚀性、硬度和机械性能。AlCr2具有体心四方结构,如图所示。处于顶角位置的是_____原子。设Cr和Al原子半径分别为rCr和rAl,则金属原子空间占有率为________% (列出计算表达式)。
Al
高考试题分析
建构模型
2.晶胞参数的计算方法
堆积模型 简单立方 堆积 体心立方 堆积 六方最密 堆积 面心立方最密堆积
晶胞
配位数 6 8 12 12
【回归基础】常见金属晶体结构分析:原子空间利用率
原子半径(r)和晶胞边长(a)的关系 2r=a 2r= (A2) 2r=a (A3) 2r=
(A1)
一个晶胞内原子数目 1 2 2 4
原子空间利用率 52% 68% 74% 74%
【自主整理】思维建模晶胞相关计算
1.(2022·湖南等级考·节选)钾、铁、硒可以形成一种超导材料,其晶胞在xz、yz和xy平面投影分别如图所示:
(1)该超导材料的最简化学式为________________;
(2)Fe原子的配位数为____________;
(3)该晶胞参数a=b=0.4 nm、c=1.4 nm。阿伏加德罗常数的值为NA,则该晶体的密度为_________g·cm-3(列出计算式)。
当堂巩固提升
2、一种四方结构的超导化合物的晶胞如图1所示。晶胞中Sm和As原子的投影位置如图2所示。
当堂巩固提升
图中F-和O2-共同占据晶胞的上下底面位置,若两者的比例依次用x和1-x代表,则该化合物的化学式表示为______;通过测定密度ρ和晶胞参数,可以计算该物质的x值,完成它们关系表达式:ρ=______g·cm-3。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子分数坐标,例如图1中原子1的坐标为 ,则原子2和3的坐标分别为____、____。
3.某种钛酸钴(CoTiO3)晶胞沿x、y或z轴任意一个方向的投影如图所示。晶胞中Co处于各顶角位置,则O处于
位置,与Co紧邻的O的个数为 。若晶胞中Co与O之间的最短距离为a nm,阿伏加德罗常数的值为NA,该晶体的密度为____________g·cm-3(列出计算式即可)。
1
3
2
4
百尺竿头 更进一步 加油,同学们!
谢谢大家!
同课章节目录
