期中填空题归类复习(专项突破)-小学数学五年级下册苏教版(带答案)
文档属性
| 名称 | 期中填空题归类复习(专项突破)-小学数学五年级下册苏教版(带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 211.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 19:41:15 | ||
图片预览


文档简介
期中填空题归类复习(专项突破)-小学数学五年级下册苏教版
1.二月份,食堂吃了大米总数的,把( )看做单位“1”,平均分成( )份,吃了的占这样的( )份。小红走了千米,把( )看做单位“1”,平均分成( )份,已走的有( )份。
2.已知(且为整数),那么和的最大公因数是( ),最小公倍数是( )。
3.1路和2路公共汽车在早上7时同时从站里发出第一辆车,以后1路车每8分钟发一辆,2路车每10分钟发一辆。那么这两路车第二次同时发车的时间是( )。
4.5箱苹果,每箱9千克,平均分给7个班,每班分得这些苹果的,是箱。
5.在、、、、,方程有( ),等式有( )。
6.学校合唱队男生人数占总人数的,女生人数比男生多。
7.在2048至少减去( )就是3的倍数,至少加上( )就有因数5。
8.的分数单位是( ),再加上( )个这样的分数单位就是1。
9.18和24的最大公因数是( );12和16的最小公倍数是( )。
10.7分米=米 49千克=吨 31分=时
11.一个三位数26□,如果它是3的倍数,那么□里最大填( );如果它同时是2、5的倍数,那么□里只能填( )。
12.一个数的最小倍数是36,这个数是( ),把它分解质因数是( )。
13.如果4x+36=72,那么8x-6x=( ),12x÷3=( )。
14.一个三位数,百位上的数既不是质数也不是合数,个位上的数既是质数又是偶数,十位上的数是0,这个数是( ),并把它分解质因数( )。
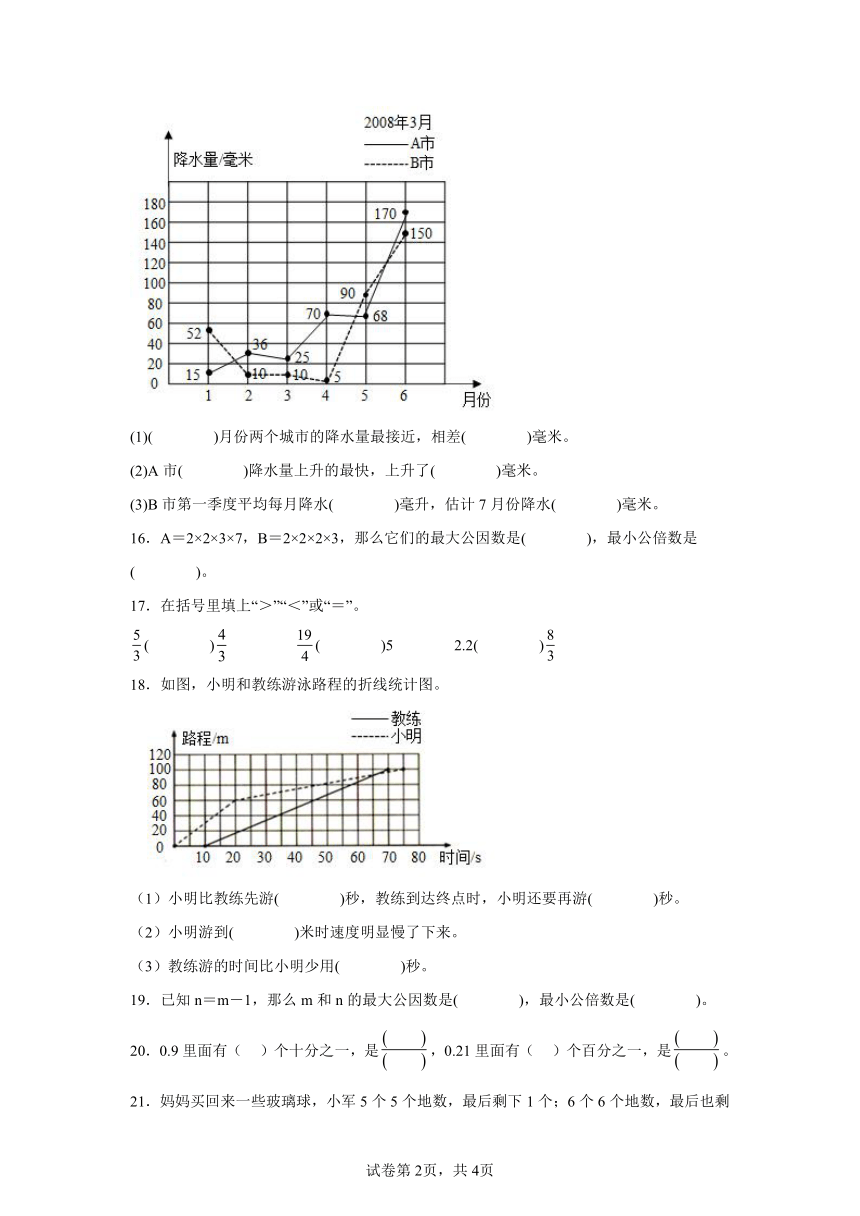
15.下面是A、B两市2008年上半年降水量情况统计图。
(1)( )月份两个城市的降水量最接近,相差( )毫米。
(2)A市( )降水量上升的最快,上升了( )毫米。
(3)B市第一季度平均每月降水( )毫升,估计7月份降水( )毫米。
16.A=2×2×3×7,B=2×2×2×3,那么它们的最大公因数是( ),最小公倍数是( )。
17.在括号里填上“>”“<”或“=”。
( ) ( )5 2.2( )
18.如图,小明和教练游泳路程的折线统计图。
(1)小明比教练先游( )秒,教练到达终点时,小明还要再游( )秒。
(2)小明游到( )米时速度明显慢了下来。
(3)教练游的时间比小明少用( )秒。
19.已知n=m-1,那么m和n的最大公因数是( ),最小公倍数是( )。
20.0.9里面有( )个十分之一,是,0.21里面有( )个百分之一,是。
21.妈妈买回来一些玻璃球,小军5个5个地数,最后剩下1个;6个6个地数,最后也剩下1个。这些玻璃球至少有( )个。
22.小明家的电话号码是由7位数字组成的AB3C5DE。其中A的最大因数是8,B既不是质数也不是合数,C是最小的合数,D有因数2和3,E既是奇数也是合数。小明家的电话号码是( )。
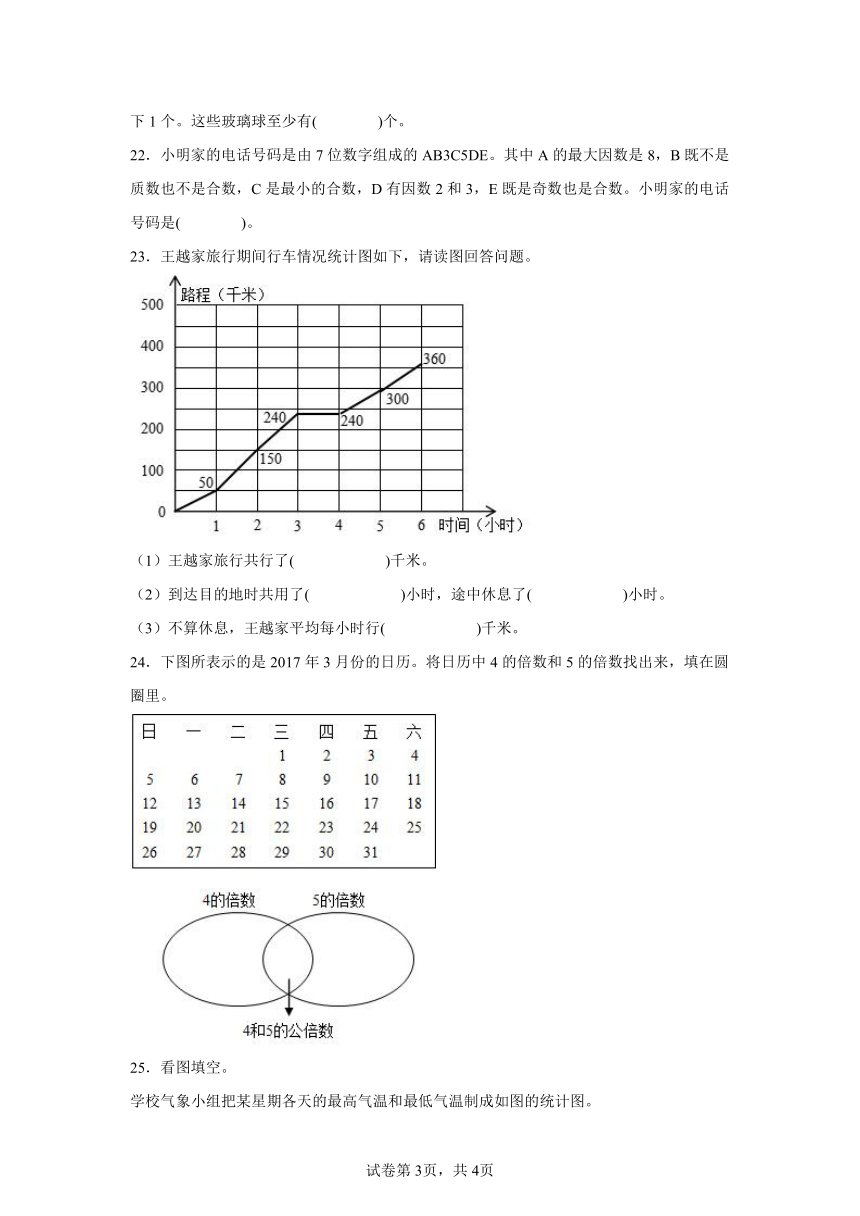
23.王越家旅行期间行车情况统计图如下,请读图回答问题。
(1)王越家旅行共行了( )千米。
(2)到达目的地时共用了( )小时,途中休息了( )小时。
(3)不算休息,王越家平均每小时行( )千米。
24.下图所表示的是2017年3月份的日历。将日历中4的倍数和5的倍数找出来,填在圆圈里。
25.看图填空。
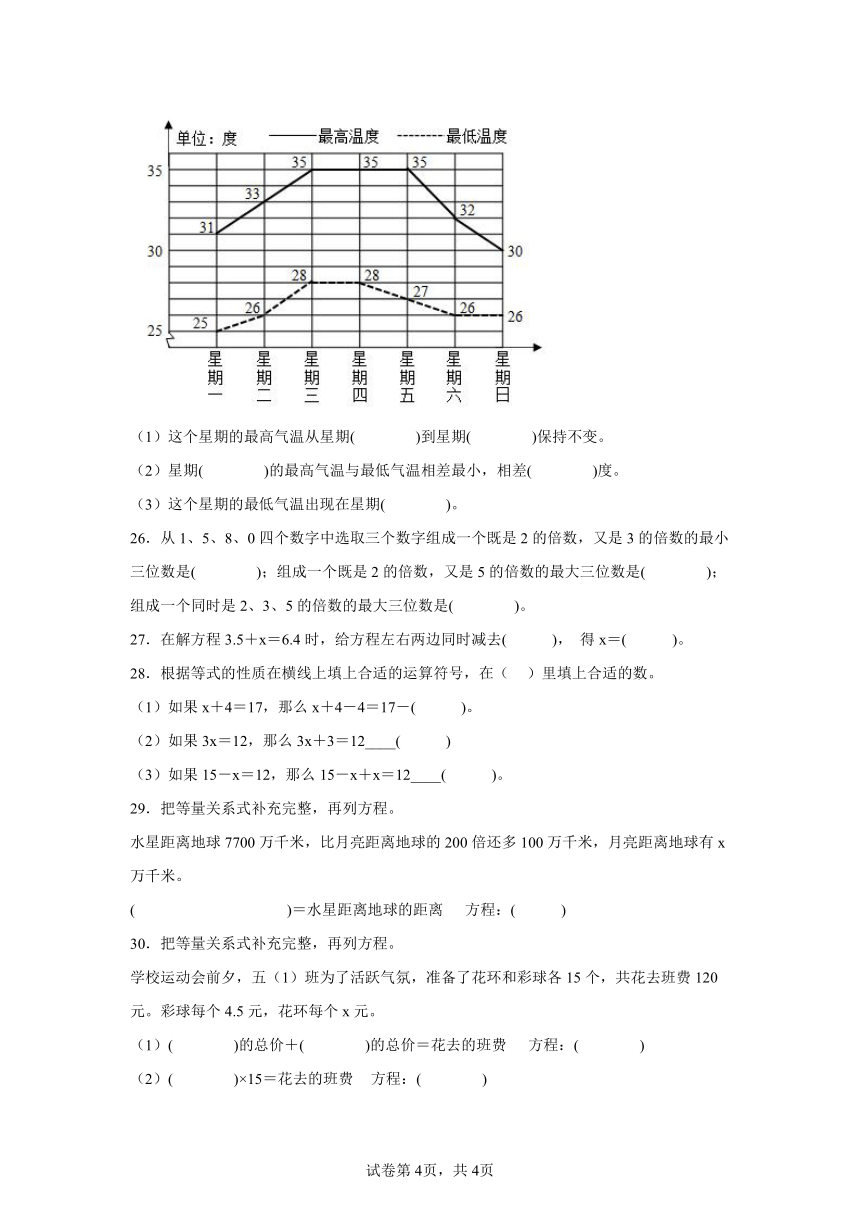
学校气象小组把某星期各天的最高气温和最低气温制成如图的统计图。
(1)这个星期的最高气温从星期( )到星期( )保持不变。
(2)星期( )的最高气温与最低气温相差最小,相差( )度。
(3)这个星期的最低气温出现在星期( )。
26.从1、5、8、0四个数字中选取三个数字组成一个既是2的倍数,又是3的倍数的最小三位数是( );组成一个既是2的倍数,又是5的倍数的最大三位数是( );组成一个同时是2、3、5的倍数的最大三位数是( )。
27.在解方程3.5+x=6.4时,给方程左右两边同时减去( ), 得x=( )。
28.根据等式的性质在横线上填上合适的运算符号,在( )里填上合适的数。
(1)如果x+4=17,那么x+4-4=17-( )。
(2)如果3x=12,那么3x+3=12____( )
(3)如果15-x=12,那么15-x+x=12____( )。
29.把等量关系式补充完整,再列方程。
水星距离地球7700万千米,比月亮距离地球的200倍还多100万千米,月亮距离地球有x万千米。
( )=水星距离地球的距离 方程:( )
30.把等量关系式补充完整,再列方程。
学校运动会前夕,五(1)班为了活跃气氛,准备了花环和彩球各15个,共花去班费120元。彩球每个4.5元,花环每个x元。
(1)( )的总价+( )的总价=花去的班费 方程:( )
(2)( )×15=花去的班费 方程:( )
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 大米总数 7 4 1千米 5 4
【分析】根据题意,把大米总数看做单位“1”,将单位“1”平均分成若干份,表示这样一份或几份的数为分数;把1千米数看做单位“1”,将单位“1”平均分成若干份,表示这样一份或几份的数为分数。据此分析填空即可。
【详解】二月份,食堂吃了大米总数的,把大米总数看做单位“1”,平均分成7份,吃了的占这样的4份。小红走了千米,把1千米看做单位“1”,平均分成5份,已走的有4份。
【点睛】此题考查分数的意义和分数单位的辨识及应用。
2. 1 ab
【分析】根据题意,a-b=1(b>0且为整数),a和b是相邻的两个数;即a和b为互质数;如果两个数为互质数,最大公因数是1,最小公倍数是两个数的乘积,据此解答。
【详解】根据分析可知,已知a-b=1(b>0且为整数),那么a和b的最大公因数是1,最小公倍数是ab。
【点睛】本题考查互质数的两个数的最大公因数和最小公倍数的求法。
3.早上7时40分
【分析】1路车每隔8分钟发一辆,2路车每隔10分钟发一辆,它们同时发车的间隔时间是8与10的最小公倍数;与此求出它们下次再发车需要经过的时间;然后再从7时向后推算即可。
【详解】8=2×2×2
10=2×5
所以10和8的最小公倍数是:2×2×2×5=40;
再过40分钟第二次同时发车;
7时+40分=7时40分;
这两路车早上7时40分第二次同时发车。
【点睛】本题关键是找出他们每两次同时出发之间相隔的时间,进而根据开始的时刻推算求解。
4.;
【分析】把苹果的总箱数看作单位“1”,把它平均分成7份,求每班分得这些苹果的几分之几,用“1”除以班数;求每份的箱数,用总箱数除以班数。
【详解】
(箱)
【点睛】解决本题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
5. , ,,
【分析】方程必须满足两个条件(缺一不可):1、含有未知数;2、是等式。含有等号的式子叫做等式。根据方程和等式的特点进行判断即可。
【详解】,是等式也是方程;
,是等式不是方程;
,既不是等式也不是方程;
,是等式也是方程;
,既不是等式也不是方程。
【点睛】本题考查了方程与等式的区别。
6.
【分析】根据题意,如果男生人数占总人数的,就是9份中的4份是男生,那么5份就是女生,求女生比男生多几分之几,用女生和男生的差除以男生即可解答。
【详解】(9-4-4)÷4
=1÷4
=
【点睛】此题主要考查学生对分数意义的理解与应用。
7. 2 2
【分析】各个数位上数字的和是3的倍数,这个数就是3的倍数,2048各个数位上的数字的和是2+0+4+8=14,至少再减去2就是3的倍数;个位上是0或5的数就是5的倍数,2048的个位上是8,至少再加上2,即8+2=10,变成个位上是0,据此解答。
【详解】根据分析可知,在2048只少减去2就是3的倍数,至少加上2就有因数5。
【点睛】本题考查3和5的倍数特征,根据3和 5的倍数特征进行解答。
8. 4
【分析】将单位“1”平均分成若干份,表示其中这样一份的数为分数。由此可知,的分数单位是,1-=,里含有4个,所以再加上4个这样的分数单位就是1。
【详解】根据分数单位的意义可知,的分数单位是,
1-=,里含有4个,所以再加上4个这样的分数单位就是1。
【点睛】一个分数的分母是几,其分数单位就是几分之一。
9. 6 48
【分析】求最大公因数也就是几个数的公有质因数的连乘积,对于这两个数来说:两个数的公有质因数连乘积就是它们的最大公因数,两个数的公有质因数和它们独有的质因数的连乘积就是它们的最小公倍数,由此解决问题即可。
【详解】18和24的最大公因数:
18=2×3×3
24=2×2×2×3
最大公因数是:2×3=6;
12和16最小公倍数:
12=2×2×3
16=2×2×2×2
最小公倍数是:2×2×2×2×3=48。
【点睛】本题考查最大公因数和最小公倍数的求法。
10.;;
【分析】低级单位换算成高级单位,用低级单位上的数除以它们之间的进率;据此解答,结果用分数表示。
【详解】7分米=米 49千克=吨 31分=时
【点睛】此题考查的是长度、质量、时间之间的单位换算,关键是要掌握它们之间的进率。
11. 7 0
【分析】一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。同时是2和5的倍数的特征:个位上的数字是0;据此解答。
【详解】根据3的倍数特征,2+6+□的和是3的倍数,所以□里可以填1、4、7,最大是7;
根据同时是2和5的倍数的特征可知:如果26□是2、5的倍数,那么□里只能填0。
【点睛】本题主要考查2、3、和5的倍数特征。
12. 36 36=2×2×3×3
【分析】根据“一个数的最大因数和最小倍数都是它本身”,求出这个数,再根据分解质因数的方法,把36写出几个质数相乘的形式,即可解答。
【详解】一个数的最小倍数是36,这个数是36;
36=2×2×3×3
【点睛】本题考查因数与倍数的意义,以及分解质因数的方法。
13. 18 36
【分析】先根据等式的性质求出4x+36=72中x的值,然后代入到8x-6x、12x÷3中求值即可。
【详解】4x+36=72
解:4x=72-36
4x=36
x=9
把x=9代入到8x-6x中,
8x-6x=8×9-6×9=72-54=18;
把x=9代入到12x÷3中,
12x÷3=12×9÷3=36。
【点睛】此题考查的是依据等式的性质解方程和求含有字母的式子的值。
14. 102 102=2×3×17
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;除了1和它本身外,还有别的因数的数叫合数,既不是质数也不是合数,这个数是1;能被2整除的数叫偶数,即是质数又是偶数,这个数是2;十位上的数是0,由此写出这个数。再利用短除法将这个数分解质因数即可得解。
【详解】根据分析可知,这个数是102
102=2×3×17
【点睛】本题关键是要明白质数、合数、偶数的定义,并且要牢记10以内的质数、合数和偶数。
15.(1) 3 15
(2) 5月份到6月份 102
(3) 24 180
【分析】(1)观察统计图,找出哪个月份两市的降水量最接近;再求出两者的差;
(2)观察统计图,找出A市的哪个月份到哪个月份降水量上升的最快,求出两月份的降水量的差;
(3)根据平均数的求法,求出B市的第一季度的平均每月降水量;再根据4到6月份的降水量,估计7月份的降水量。
【详解】(1)25-10=15(毫米)
3月份的两个城市的降水量最接近,相差15毫米。
(2)170-68=102(毫米)
A市5月份到6月份降水量上升最快,上升102毫升。
(3)(52+10+10)÷3
=(62+10)÷3
=72÷3
=24(毫升)
估计7月份降水180毫升。
【点睛】本题主要考查根据复式折线统计图中的有关信息,分析并解决有关问题。
16. 12 168
【分析】两个数的共有质因数连乘积是最大公因数;最小公倍数是两个数的共有质因数与独有质因数的连乘积;据此解答。
【详解】A=2×2×3×7
B=2×2×2×3
A和B的最大公因数:2×2×3
=4×3
=12
最小公倍数:2×2×3×7×2
=4×3×7×2
=12×7×2
=84×2
=168
【点睛】本题考查最大公因数和最小公倍数的求法。
17. > < <
【分析】同分母分数,分子越大,这个分数越大;把整数化成假分数,再比较;把假分数化成带分数,再比较。
【详解】> 5=,<5 =2 ,2.2=2 ,所以 2.2<
【点睛】此题考查了分数的大小比较以及分数与小数的比较,选择适当的方法解答即可。
18. 10 5 60 15
【分析】(1)根据折线统计图,小明和教练的起点位置判断即可。
(2)根据表示小明游泳状态的虚线即可得出:小明游到60米时,速度明显慢了下来。
(3)根据线统计图,用小明的结束时间-开始时间,求出小明的游泳时间;再用教练结束时间-开始时间,求出教练的游泳时间,然后再作比较即可。
【详解】(1)观察折线统计图,小明比教练先游10秒,教练到达终点时,小明还要再游5秒。
(2)小明游到60米时,速度明显慢了下来。
(3)小明用时75秒,教练70-10=60(秒)
75-60=15(秒)
【点睛】本题主要考查复式折线统计图,关键根据折线统计图的特点做题。
19. 1 mn
【分析】已知n=m-1,所以m-n=1,m和n是相邻的两个数,m和n为互质数;根据互质数的最大公因数与最小公倍数的求法:最大公因数是1;最小公倍数是两个数的乘积;据此解答。
【详解】n=m-1
m-n=1
m与n是相邻的两个数;m和n是互质数。
已知n=m-1,那么m 和n的最大公因数是1,最小公倍数是mn。
【点睛】本题考查互质数的两个数的最大公因数与最小公倍数的求法。
20.9;;21;
【分析】0.9表示9个0.1,也就是9个十分之一,是 ,0.21里面有21个0.01,也就是21个百分之一,是 ,据此填空即可。
【详解】0.9里面有9个十分之一,是,0.21里面有21个百分之一,是。
【点睛】此题考查了分数的基本认识,比较简单。
21.31
【分析】由“5个5个数地数最后剩1个,6个6个地数,最后也剩1个”可知:妈妈买回来的玻璃球是5和6的最小公倍数加上1,求出5和6的最小公倍数再加上1,即可解答。
【详解】5和6的最小公倍数为:5×6=30
30+1=31(个)
【点睛】本题考查求两个数最小公倍数,关键明确求出的最小公倍数要加上1。
22.8134569
【分析】一个数最大的因数是它本身;A的最大因数是8,A是8;B既不是质数也不是合数,这个数是1;C是最小的合数,最小合数是4,C是4;D有因数2和3,D是2和3的最小公倍数,最小公倍数是6;E即是奇数也是合数,1到9中,即是奇数又是合数的数是9,据此解答。
【详解】根据分析可知,小明家的电话号码由7位数字组成的AB3C5DE,电话号码是8134569。
【点睛】解答本题的关键是根据给出的编号找出各个位上数字的含义,再根据各个上数字的含义进行解答。
23. 360 6 1 72
【分析】折线统计图要注意观察横坐标和纵坐标的数值,纵坐标代表王越走的路程,横坐标代表王越走路所花的时间。
【详解】纵坐标的最后一个位置落在360千米,说明共行了360千米。横坐标显示最后停止的时间为6小时,说明共用了6小时,横坐标3小时和4小时之间折线是水平的,路程没有变化,说明这时王越正在休息,休息的时间为1小时,走路花了5小时。所以王越的速度=路程÷时间(千米/时)。
【点睛】此题的解题关键是理解折线统计图,仔细观察折线的起伏,它可以表示数量的多少和增减变化情况。
24.见详解
【分析】结合2017年3月份的日历和4的倍数特征,4的倍数有:4,8,12,16,20,24,28;5的倍数有5,10,15,20,25,30,公倍数是20。据此作答。
【详解】根据分析,填空如下:
【点睛】本题考查4和5的倍数特征及公倍数的求法,要熟练掌握2和5的倍数特征。
25. 三 五 日 4 一
【分析】(1)由统计图即可看出这个星期的最高气温从星期几到星期几保持不变,即折线与横轴平行。
(2)根据图中表示的这一星期每天的最高气温与最低的点相差的距离即可确定哪天相差最小;用表示这天的最高气温减最低温度就是相差的温度。
(3)由统计图即可看出这个星期的最低气温出现在星期一。
【详解】(1)由统计图可看出,从星期三到星期五,最高气温都是35度,保持不变。
(2)星期一:31-25=6度
星期二:33-26=7度
星期三:35-28=7度
星期四:35-28=7度
星期五:35-27=8度
星期六:32-26=6度
星期日:30-26=4度
星期日的最高气温与最低气温相差最小,相差4度。
(3)由统计图可看出这个星期的最低气温是25度,出现在星期一。
【点睛】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题。
26. 108 850 810
【分析】一个数如果同时是2、3的倍数,这个数的个位必须是偶数,各位上的数字之和是3的倍数,根据这一特征,用1、5、0即可组成既是2的倍数,又是3的倍数的三位数,其中百位为1,十位为0,个位数字为8;一个数既是2的倍数,又是5的倍数,末尾必须是0,根据这一特征,用5、8、0即可组成这样一个最大三位数,其中百位为8,十位为5,个位数字为0;一个同时是2、3、5的倍数的数,末尾必须是0而且各位上的数字之和是3的倍数,根据这一特征,可用1、8、0这三个数字组成这个最大三位数,其中百位为8,十位为1,个位数字为0。据此作答。
【详解】根据分析得:从1、5、8、0四个数字中选取三个数字组成一个既是2的倍数,又是3的倍数的最小三位数是108;组成一个既是2的倍数,又是5的倍数的最大三位数是850;组成一个同时是2、3、5的倍数的最大三位数是810。
【点睛】本题主要考查2、3、5的倍数特征,注意本题要先满足个位是0,就是满足是2和5的倍数,然后再满足是3的倍数,即各个数位上的和是3的倍数。
27. 3.5 2.9
【分析】等式的性质:等式两边同时加上或减去同一个数,所得结果还是等式,据此解答。
【详解】在解方程3.5+x=6.4时,给方程左右两边同时减去3.5,得x=2.9。
故答案为:3.5;2.9
【点睛】等式的性质是解方程的依据,学生应熟练掌握。
28. 4 + 3 + x
【分析】等式的性质:等式两边同时加上或减去同一个数,所得结果还是等式,据此解答。
【详解】(1)如果x+4=17,那么x+4-4=17-4。
(2)如果3x=12,那么3x+3=12+3。
(3)如果15-x=12,那么15-x+x=12+x。
故答案为:4;+;3;+;x
【点睛】等式的性质是解答此题的依据,学生应熟记。
29. 月亮距离地球的距离的200倍+100万千米 200x+100=7700
【分析】月亮距离地球有x万千米,月亮距离地球的200倍为:200x(万千米),等量关系式:月亮距离地球的距离的200倍+100万千米=水星距离地球的距离,据此列方程。
【详解】根据分析可知,月亮距离地球的距离的200倍+100万千米=水星距离地球的距离,列方程:200x+100=7700。
【点睛】等量关系式是表达数量间的相等关系的式子,如果要求用方程解答时,就需找出题中的等量关系,从而列出等量关系式。
30. 花环 彩球 15x+4.5×15=120 1个花环和1个彩球的价钱之和 (4.5+x)×15=120
【分析】根据题意可知,(1)数量关系式:花环的总价+彩球的总价=花去的班费;彩球每个4.5元,花环每个x元,数量各15个,根据单价×数量=总价,求出花环的总价和彩球的总价,据此列方程。
(2)数量关系式:1个花环和1个彩球的价钱之和×15=花去的班费,据此列方程。
【详解】根据分析可知,(1)数量关系式:花环的总价+彩球的总价=花去的班费,列方程:15x+4.5×15=120。
(2)数量关系式:1个花环和1个彩球的价钱之和×15=花去的班费,列方程:(4.5+x)×15=120。
【点睛】本题考查了对实际问题的分析能力及用方程解决问题的能力。
答案第1页,共2页
答案第1页,共2页
1.二月份,食堂吃了大米总数的,把( )看做单位“1”,平均分成( )份,吃了的占这样的( )份。小红走了千米,把( )看做单位“1”,平均分成( )份,已走的有( )份。
2.已知(且为整数),那么和的最大公因数是( ),最小公倍数是( )。
3.1路和2路公共汽车在早上7时同时从站里发出第一辆车,以后1路车每8分钟发一辆,2路车每10分钟发一辆。那么这两路车第二次同时发车的时间是( )。
4.5箱苹果,每箱9千克,平均分给7个班,每班分得这些苹果的,是箱。
5.在、、、、,方程有( ),等式有( )。
6.学校合唱队男生人数占总人数的,女生人数比男生多。
7.在2048至少减去( )就是3的倍数,至少加上( )就有因数5。
8.的分数单位是( ),再加上( )个这样的分数单位就是1。
9.18和24的最大公因数是( );12和16的最小公倍数是( )。
10.7分米=米 49千克=吨 31分=时
11.一个三位数26□,如果它是3的倍数,那么□里最大填( );如果它同时是2、5的倍数,那么□里只能填( )。
12.一个数的最小倍数是36,这个数是( ),把它分解质因数是( )。
13.如果4x+36=72,那么8x-6x=( ),12x÷3=( )。
14.一个三位数,百位上的数既不是质数也不是合数,个位上的数既是质数又是偶数,十位上的数是0,这个数是( ),并把它分解质因数( )。
15.下面是A、B两市2008年上半年降水量情况统计图。
(1)( )月份两个城市的降水量最接近,相差( )毫米。
(2)A市( )降水量上升的最快,上升了( )毫米。
(3)B市第一季度平均每月降水( )毫升,估计7月份降水( )毫米。
16.A=2×2×3×7,B=2×2×2×3,那么它们的最大公因数是( ),最小公倍数是( )。
17.在括号里填上“>”“<”或“=”。
( ) ( )5 2.2( )
18.如图,小明和教练游泳路程的折线统计图。
(1)小明比教练先游( )秒,教练到达终点时,小明还要再游( )秒。
(2)小明游到( )米时速度明显慢了下来。
(3)教练游的时间比小明少用( )秒。
19.已知n=m-1,那么m和n的最大公因数是( ),最小公倍数是( )。
20.0.9里面有( )个十分之一,是,0.21里面有( )个百分之一,是。
21.妈妈买回来一些玻璃球,小军5个5个地数,最后剩下1个;6个6个地数,最后也剩下1个。这些玻璃球至少有( )个。
22.小明家的电话号码是由7位数字组成的AB3C5DE。其中A的最大因数是8,B既不是质数也不是合数,C是最小的合数,D有因数2和3,E既是奇数也是合数。小明家的电话号码是( )。
23.王越家旅行期间行车情况统计图如下,请读图回答问题。
(1)王越家旅行共行了( )千米。
(2)到达目的地时共用了( )小时,途中休息了( )小时。
(3)不算休息,王越家平均每小时行( )千米。
24.下图所表示的是2017年3月份的日历。将日历中4的倍数和5的倍数找出来,填在圆圈里。
25.看图填空。
学校气象小组把某星期各天的最高气温和最低气温制成如图的统计图。
(1)这个星期的最高气温从星期( )到星期( )保持不变。
(2)星期( )的最高气温与最低气温相差最小,相差( )度。
(3)这个星期的最低气温出现在星期( )。
26.从1、5、8、0四个数字中选取三个数字组成一个既是2的倍数,又是3的倍数的最小三位数是( );组成一个既是2的倍数,又是5的倍数的最大三位数是( );组成一个同时是2、3、5的倍数的最大三位数是( )。
27.在解方程3.5+x=6.4时,给方程左右两边同时减去( ), 得x=( )。
28.根据等式的性质在横线上填上合适的运算符号,在( )里填上合适的数。
(1)如果x+4=17,那么x+4-4=17-( )。
(2)如果3x=12,那么3x+3=12____( )
(3)如果15-x=12,那么15-x+x=12____( )。
29.把等量关系式补充完整,再列方程。
水星距离地球7700万千米,比月亮距离地球的200倍还多100万千米,月亮距离地球有x万千米。
( )=水星距离地球的距离 方程:( )
30.把等量关系式补充完整,再列方程。
学校运动会前夕,五(1)班为了活跃气氛,准备了花环和彩球各15个,共花去班费120元。彩球每个4.5元,花环每个x元。
(1)( )的总价+( )的总价=花去的班费 方程:( )
(2)( )×15=花去的班费 方程:( )
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 大米总数 7 4 1千米 5 4
【分析】根据题意,把大米总数看做单位“1”,将单位“1”平均分成若干份,表示这样一份或几份的数为分数;把1千米数看做单位“1”,将单位“1”平均分成若干份,表示这样一份或几份的数为分数。据此分析填空即可。
【详解】二月份,食堂吃了大米总数的,把大米总数看做单位“1”,平均分成7份,吃了的占这样的4份。小红走了千米,把1千米看做单位“1”,平均分成5份,已走的有4份。
【点睛】此题考查分数的意义和分数单位的辨识及应用。
2. 1 ab
【分析】根据题意,a-b=1(b>0且为整数),a和b是相邻的两个数;即a和b为互质数;如果两个数为互质数,最大公因数是1,最小公倍数是两个数的乘积,据此解答。
【详解】根据分析可知,已知a-b=1(b>0且为整数),那么a和b的最大公因数是1,最小公倍数是ab。
【点睛】本题考查互质数的两个数的最大公因数和最小公倍数的求法。
3.早上7时40分
【分析】1路车每隔8分钟发一辆,2路车每隔10分钟发一辆,它们同时发车的间隔时间是8与10的最小公倍数;与此求出它们下次再发车需要经过的时间;然后再从7时向后推算即可。
【详解】8=2×2×2
10=2×5
所以10和8的最小公倍数是:2×2×2×5=40;
再过40分钟第二次同时发车;
7时+40分=7时40分;
这两路车早上7时40分第二次同时发车。
【点睛】本题关键是找出他们每两次同时出发之间相隔的时间,进而根据开始的时刻推算求解。
4.;
【分析】把苹果的总箱数看作单位“1”,把它平均分成7份,求每班分得这些苹果的几分之几,用“1”除以班数;求每份的箱数,用总箱数除以班数。
【详解】
(箱)
【点睛】解决本题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
5. , ,,
【分析】方程必须满足两个条件(缺一不可):1、含有未知数;2、是等式。含有等号的式子叫做等式。根据方程和等式的特点进行判断即可。
【详解】,是等式也是方程;
,是等式不是方程;
,既不是等式也不是方程;
,是等式也是方程;
,既不是等式也不是方程。
【点睛】本题考查了方程与等式的区别。
6.
【分析】根据题意,如果男生人数占总人数的,就是9份中的4份是男生,那么5份就是女生,求女生比男生多几分之几,用女生和男生的差除以男生即可解答。
【详解】(9-4-4)÷4
=1÷4
=
【点睛】此题主要考查学生对分数意义的理解与应用。
7. 2 2
【分析】各个数位上数字的和是3的倍数,这个数就是3的倍数,2048各个数位上的数字的和是2+0+4+8=14,至少再减去2就是3的倍数;个位上是0或5的数就是5的倍数,2048的个位上是8,至少再加上2,即8+2=10,变成个位上是0,据此解答。
【详解】根据分析可知,在2048只少减去2就是3的倍数,至少加上2就有因数5。
【点睛】本题考查3和5的倍数特征,根据3和 5的倍数特征进行解答。
8. 4
【分析】将单位“1”平均分成若干份,表示其中这样一份的数为分数。由此可知,的分数单位是,1-=,里含有4个,所以再加上4个这样的分数单位就是1。
【详解】根据分数单位的意义可知,的分数单位是,
1-=,里含有4个,所以再加上4个这样的分数单位就是1。
【点睛】一个分数的分母是几,其分数单位就是几分之一。
9. 6 48
【分析】求最大公因数也就是几个数的公有质因数的连乘积,对于这两个数来说:两个数的公有质因数连乘积就是它们的最大公因数,两个数的公有质因数和它们独有的质因数的连乘积就是它们的最小公倍数,由此解决问题即可。
【详解】18和24的最大公因数:
18=2×3×3
24=2×2×2×3
最大公因数是:2×3=6;
12和16最小公倍数:
12=2×2×3
16=2×2×2×2
最小公倍数是:2×2×2×2×3=48。
【点睛】本题考查最大公因数和最小公倍数的求法。
10.;;
【分析】低级单位换算成高级单位,用低级单位上的数除以它们之间的进率;据此解答,结果用分数表示。
【详解】7分米=米 49千克=吨 31分=时
【点睛】此题考查的是长度、质量、时间之间的单位换算,关键是要掌握它们之间的进率。
11. 7 0
【分析】一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。同时是2和5的倍数的特征:个位上的数字是0;据此解答。
【详解】根据3的倍数特征,2+6+□的和是3的倍数,所以□里可以填1、4、7,最大是7;
根据同时是2和5的倍数的特征可知:如果26□是2、5的倍数,那么□里只能填0。
【点睛】本题主要考查2、3、和5的倍数特征。
12. 36 36=2×2×3×3
【分析】根据“一个数的最大因数和最小倍数都是它本身”,求出这个数,再根据分解质因数的方法,把36写出几个质数相乘的形式,即可解答。
【详解】一个数的最小倍数是36,这个数是36;
36=2×2×3×3
【点睛】本题考查因数与倍数的意义,以及分解质因数的方法。
13. 18 36
【分析】先根据等式的性质求出4x+36=72中x的值,然后代入到8x-6x、12x÷3中求值即可。
【详解】4x+36=72
解:4x=72-36
4x=36
x=9
把x=9代入到8x-6x中,
8x-6x=8×9-6×9=72-54=18;
把x=9代入到12x÷3中,
12x÷3=12×9÷3=36。
【点睛】此题考查的是依据等式的性质解方程和求含有字母的式子的值。
14. 102 102=2×3×17
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;除了1和它本身外,还有别的因数的数叫合数,既不是质数也不是合数,这个数是1;能被2整除的数叫偶数,即是质数又是偶数,这个数是2;十位上的数是0,由此写出这个数。再利用短除法将这个数分解质因数即可得解。
【详解】根据分析可知,这个数是102
102=2×3×17
【点睛】本题关键是要明白质数、合数、偶数的定义,并且要牢记10以内的质数、合数和偶数。
15.(1) 3 15
(2) 5月份到6月份 102
(3) 24 180
【分析】(1)观察统计图,找出哪个月份两市的降水量最接近;再求出两者的差;
(2)观察统计图,找出A市的哪个月份到哪个月份降水量上升的最快,求出两月份的降水量的差;
(3)根据平均数的求法,求出B市的第一季度的平均每月降水量;再根据4到6月份的降水量,估计7月份的降水量。
【详解】(1)25-10=15(毫米)
3月份的两个城市的降水量最接近,相差15毫米。
(2)170-68=102(毫米)
A市5月份到6月份降水量上升最快,上升102毫升。
(3)(52+10+10)÷3
=(62+10)÷3
=72÷3
=24(毫升)
估计7月份降水180毫升。
【点睛】本题主要考查根据复式折线统计图中的有关信息,分析并解决有关问题。
16. 12 168
【分析】两个数的共有质因数连乘积是最大公因数;最小公倍数是两个数的共有质因数与独有质因数的连乘积;据此解答。
【详解】A=2×2×3×7
B=2×2×2×3
A和B的最大公因数:2×2×3
=4×3
=12
最小公倍数:2×2×3×7×2
=4×3×7×2
=12×7×2
=84×2
=168
【点睛】本题考查最大公因数和最小公倍数的求法。
17. > < <
【分析】同分母分数,分子越大,这个分数越大;把整数化成假分数,再比较;把假分数化成带分数,再比较。
【详解】> 5=,<5 =2 ,2.2=2 ,所以 2.2<
【点睛】此题考查了分数的大小比较以及分数与小数的比较,选择适当的方法解答即可。
18. 10 5 60 15
【分析】(1)根据折线统计图,小明和教练的起点位置判断即可。
(2)根据表示小明游泳状态的虚线即可得出:小明游到60米时,速度明显慢了下来。
(3)根据线统计图,用小明的结束时间-开始时间,求出小明的游泳时间;再用教练结束时间-开始时间,求出教练的游泳时间,然后再作比较即可。
【详解】(1)观察折线统计图,小明比教练先游10秒,教练到达终点时,小明还要再游5秒。
(2)小明游到60米时,速度明显慢了下来。
(3)小明用时75秒,教练70-10=60(秒)
75-60=15(秒)
【点睛】本题主要考查复式折线统计图,关键根据折线统计图的特点做题。
19. 1 mn
【分析】已知n=m-1,所以m-n=1,m和n是相邻的两个数,m和n为互质数;根据互质数的最大公因数与最小公倍数的求法:最大公因数是1;最小公倍数是两个数的乘积;据此解答。
【详解】n=m-1
m-n=1
m与n是相邻的两个数;m和n是互质数。
已知n=m-1,那么m 和n的最大公因数是1,最小公倍数是mn。
【点睛】本题考查互质数的两个数的最大公因数与最小公倍数的求法。
20.9;;21;
【分析】0.9表示9个0.1,也就是9个十分之一,是 ,0.21里面有21个0.01,也就是21个百分之一,是 ,据此填空即可。
【详解】0.9里面有9个十分之一,是,0.21里面有21个百分之一,是。
【点睛】此题考查了分数的基本认识,比较简单。
21.31
【分析】由“5个5个数地数最后剩1个,6个6个地数,最后也剩1个”可知:妈妈买回来的玻璃球是5和6的最小公倍数加上1,求出5和6的最小公倍数再加上1,即可解答。
【详解】5和6的最小公倍数为:5×6=30
30+1=31(个)
【点睛】本题考查求两个数最小公倍数,关键明确求出的最小公倍数要加上1。
22.8134569
【分析】一个数最大的因数是它本身;A的最大因数是8,A是8;B既不是质数也不是合数,这个数是1;C是最小的合数,最小合数是4,C是4;D有因数2和3,D是2和3的最小公倍数,最小公倍数是6;E即是奇数也是合数,1到9中,即是奇数又是合数的数是9,据此解答。
【详解】根据分析可知,小明家的电话号码由7位数字组成的AB3C5DE,电话号码是8134569。
【点睛】解答本题的关键是根据给出的编号找出各个位上数字的含义,再根据各个上数字的含义进行解答。
23. 360 6 1 72
【分析】折线统计图要注意观察横坐标和纵坐标的数值,纵坐标代表王越走的路程,横坐标代表王越走路所花的时间。
【详解】纵坐标的最后一个位置落在360千米,说明共行了360千米。横坐标显示最后停止的时间为6小时,说明共用了6小时,横坐标3小时和4小时之间折线是水平的,路程没有变化,说明这时王越正在休息,休息的时间为1小时,走路花了5小时。所以王越的速度=路程÷时间(千米/时)。
【点睛】此题的解题关键是理解折线统计图,仔细观察折线的起伏,它可以表示数量的多少和增减变化情况。
24.见详解
【分析】结合2017年3月份的日历和4的倍数特征,4的倍数有:4,8,12,16,20,24,28;5的倍数有5,10,15,20,25,30,公倍数是20。据此作答。
【详解】根据分析,填空如下:
【点睛】本题考查4和5的倍数特征及公倍数的求法,要熟练掌握2和5的倍数特征。
25. 三 五 日 4 一
【分析】(1)由统计图即可看出这个星期的最高气温从星期几到星期几保持不变,即折线与横轴平行。
(2)根据图中表示的这一星期每天的最高气温与最低的点相差的距离即可确定哪天相差最小;用表示这天的最高气温减最低温度就是相差的温度。
(3)由统计图即可看出这个星期的最低气温出现在星期一。
【详解】(1)由统计图可看出,从星期三到星期五,最高气温都是35度,保持不变。
(2)星期一:31-25=6度
星期二:33-26=7度
星期三:35-28=7度
星期四:35-28=7度
星期五:35-27=8度
星期六:32-26=6度
星期日:30-26=4度
星期日的最高气温与最低气温相差最小,相差4度。
(3)由统计图可看出这个星期的最低气温是25度,出现在星期一。
【点睛】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题。
26. 108 850 810
【分析】一个数如果同时是2、3的倍数,这个数的个位必须是偶数,各位上的数字之和是3的倍数,根据这一特征,用1、5、0即可组成既是2的倍数,又是3的倍数的三位数,其中百位为1,十位为0,个位数字为8;一个数既是2的倍数,又是5的倍数,末尾必须是0,根据这一特征,用5、8、0即可组成这样一个最大三位数,其中百位为8,十位为5,个位数字为0;一个同时是2、3、5的倍数的数,末尾必须是0而且各位上的数字之和是3的倍数,根据这一特征,可用1、8、0这三个数字组成这个最大三位数,其中百位为8,十位为1,个位数字为0。据此作答。
【详解】根据分析得:从1、5、8、0四个数字中选取三个数字组成一个既是2的倍数,又是3的倍数的最小三位数是108;组成一个既是2的倍数,又是5的倍数的最大三位数是850;组成一个同时是2、3、5的倍数的最大三位数是810。
【点睛】本题主要考查2、3、5的倍数特征,注意本题要先满足个位是0,就是满足是2和5的倍数,然后再满足是3的倍数,即各个数位上的和是3的倍数。
27. 3.5 2.9
【分析】等式的性质:等式两边同时加上或减去同一个数,所得结果还是等式,据此解答。
【详解】在解方程3.5+x=6.4时,给方程左右两边同时减去3.5,得x=2.9。
故答案为:3.5;2.9
【点睛】等式的性质是解方程的依据,学生应熟练掌握。
28. 4 + 3 + x
【分析】等式的性质:等式两边同时加上或减去同一个数,所得结果还是等式,据此解答。
【详解】(1)如果x+4=17,那么x+4-4=17-4。
(2)如果3x=12,那么3x+3=12+3。
(3)如果15-x=12,那么15-x+x=12+x。
故答案为:4;+;3;+;x
【点睛】等式的性质是解答此题的依据,学生应熟记。
29. 月亮距离地球的距离的200倍+100万千米 200x+100=7700
【分析】月亮距离地球有x万千米,月亮距离地球的200倍为:200x(万千米),等量关系式:月亮距离地球的距离的200倍+100万千米=水星距离地球的距离,据此列方程。
【详解】根据分析可知,月亮距离地球的距离的200倍+100万千米=水星距离地球的距离,列方程:200x+100=7700。
【点睛】等量关系式是表达数量间的相等关系的式子,如果要求用方程解答时,就需找出题中的等量关系,从而列出等量关系式。
30. 花环 彩球 15x+4.5×15=120 1个花环和1个彩球的价钱之和 (4.5+x)×15=120
【分析】根据题意可知,(1)数量关系式:花环的总价+彩球的总价=花去的班费;彩球每个4.5元,花环每个x元,数量各15个,根据单价×数量=总价,求出花环的总价和彩球的总价,据此列方程。
(2)数量关系式:1个花环和1个彩球的价钱之和×15=花去的班费,据此列方程。
【详解】根据分析可知,(1)数量关系式:花环的总价+彩球的总价=花去的班费,列方程:15x+4.5×15=120。
(2)数量关系式:1个花环和1个彩球的价钱之和×15=花去的班费,列方程:(4.5+x)×15=120。
【点睛】本题考查了对实际问题的分析能力及用方程解决问题的能力。
答案第1页,共2页
答案第1页,共2页
同课章节目录
