选择题、填空题全解对策及中等解答题满分策略(上) [上下学期通用]
文档属性
| 名称 | 选择题、填空题全解对策及中等解答题满分策略(上) [上下学期通用] |  | |
| 格式 | rar | ||
| 文件大小 | 999.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-20 21:33:00 | ||
图片预览





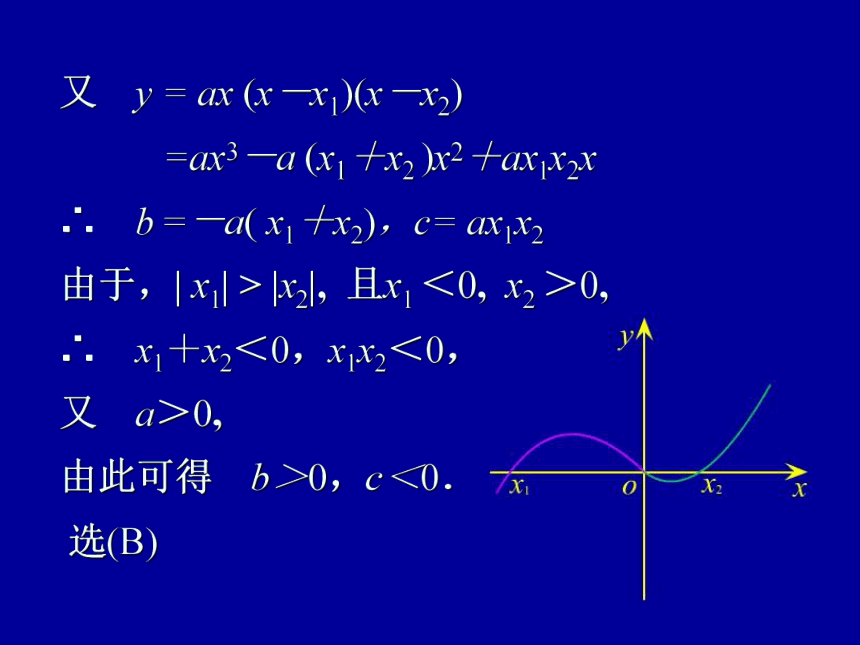


文档简介
课件64张PPT。清华同方“3+X”高分宝典数学(上)主讲:北京东城教研中心 郝澎(特级) 北京陈经纶中学 丁益祥(特级)
一、高考特点与能力要求 1.考查的内容既全面又突出重点.
2.不刻意追求单纯的记忆,突出 知识间的综合.
3.在熟练掌握基础知识的前提下,突出考查能力.
(1)通过考查数学思想和方法,突出考查能力.
(2)通过对解答速度的要求,突出考查能力.
(3)通过新题型,突出考查能力.
二、复习方法与复习建议 1.强化数形结合思想的训练
2.强化特殊化思想的训练
3.强化估值法的训练
4.适当进行新题型的训练
1.强化数形结合思想的训练
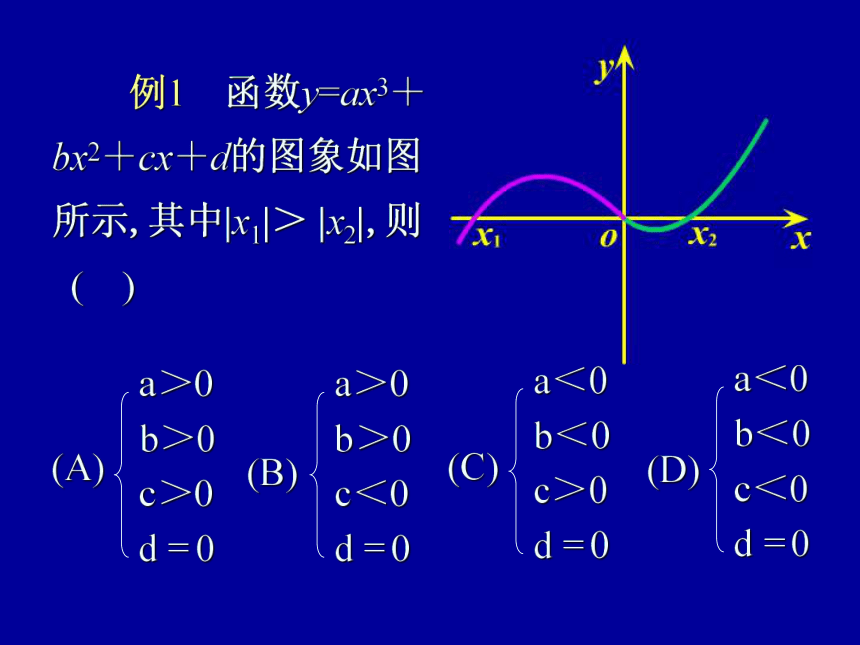
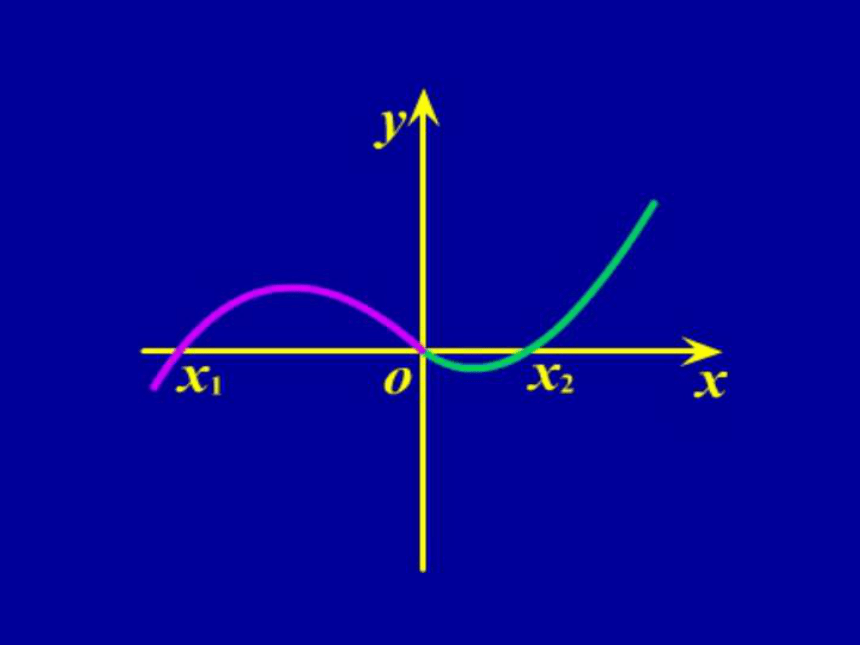
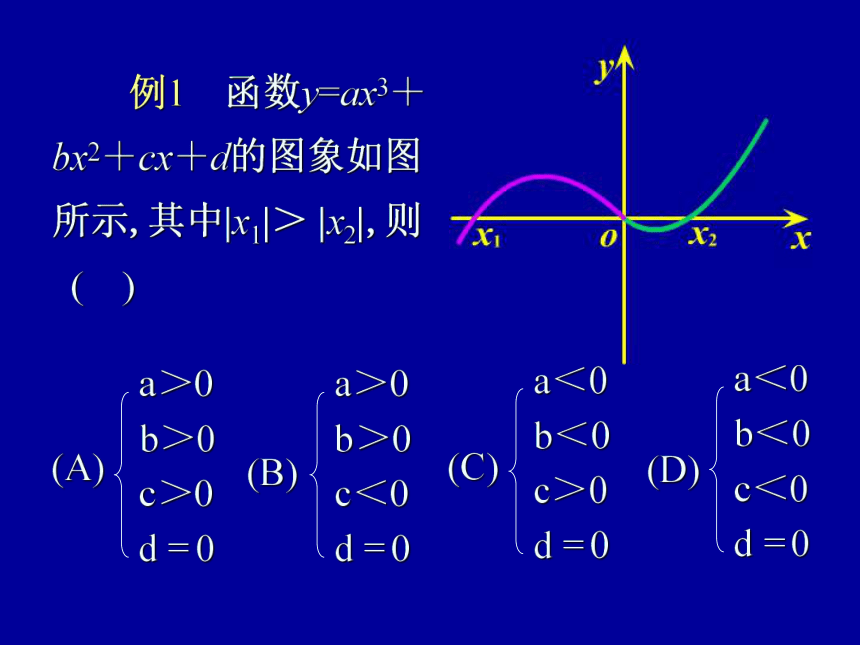
例1 函数y=ax3+
bx2+cx+d的图象如图
所示,其中|x1|> |x2|,则
( )
例1 函数y=ax3+
bx2+cx+d的图象如图
所示,其中|x1|> |x2|,则
( )
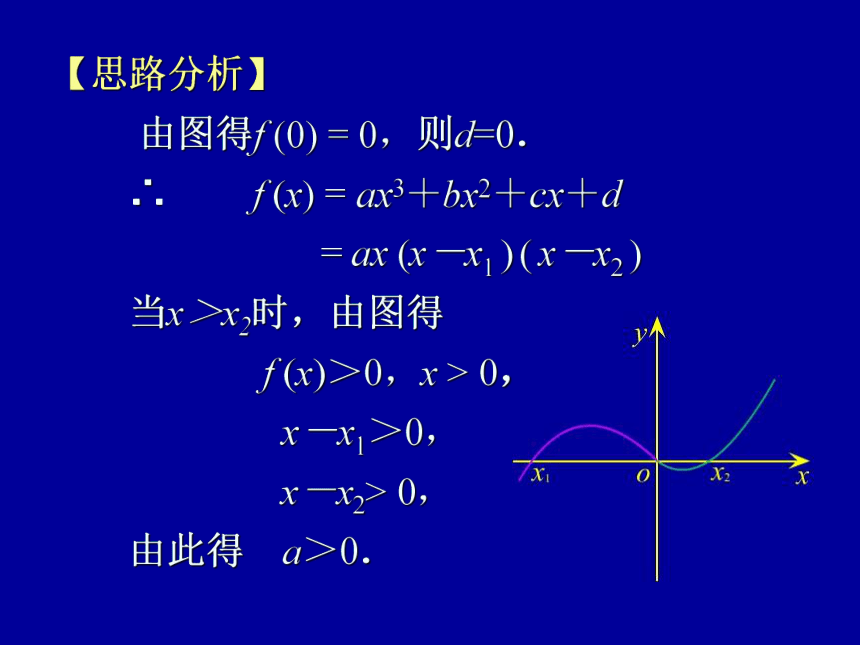
【思路分析】
由图得f (0) = 0,则d=0.
∴ f (x) = ax3+bx2+cx+d
= ax (x-x1 ) ( x-x2 )
当x>x2时,由图得
f (x)>0,x > 0,
x-x1>0,
x-x2> 0,
由此得 a>0.
又 y = ax (x-x1)(x-x2)
=ax3-a (x1+x2 )x2+ax1x2x
∴ b =-a( x1+x2),c= ax1x2
由于,| x1| > |x2|, 且x1 <0, x2 >0,
∴ x1+x2<0,x1x2<0,
又 a>0,
由此可得 b>0,c<0.
选(B) 例2 函数y=logax在x∈[2,+∞)上恒有| y |>1,则a的取值范围是( )
(A)
(B)
(C)
(D)或或 【思路分析】
令x = 2,|y | = 1,求出a = 2 或a = .
在同一坐标系内画出y = 和
的图象. 【思路分析】
令x = 2,|y | = 1,求出a = 2 或a = .
在同一坐标系内画出y = 和
的图象. 例3 复数 的辐角主值是 _________ . 【思路分析】
例3 复数 的辐角主值是 _________ . 【思路分析】
例4 已知两点A(-2,0),B(0,2),
点C是圆x2+y2-2x=0上的任意一点,则△ABC面积的最小值是( )
(A) (B)
(C) (D) 例4 已知两点A(-2,0),B(0,2),
点C是圆x2+y2-2x=0上的任意一点,则△ABC面积的最小值是( )
(A) (B)
(C) (D) 2.强化特殊化思想的训练
例5 已知函数 f (x) 对任意实数 x 都有 f (3-x) = f (2+x),它的一个单调递增区间是
[1, 2],则函数y = f (1-x) 在 ( )
(A) [-4,-3]上单调递增,[-2,-1]上单调递减
(B) [-3,-2]上单调递增,[-1, 0 ]上单调递减
(C) [-4,-3]上单调递减,[-2,-1]上单调递增
(D) [-3,-2]上单调递减,[-1, 0]上单调递增
【思路分析】
由f (3-x)=f (2+x)得y = f (x)的图象的对称轴为 .
又 f (x) 在 [1, 2] 上单调递增,
可令
则
.从图中可直观得到正确答案 (B). 例6 已知F1、F2是双曲线 (a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线的左支交于A、B两点,若△ABF2为正三角形, 那么该双曲线的离心率为( )
(A) (B) (C) 2 (D) 3【思路分析】(一)
,
由ABF2为正三角形得
即
将b2=c2-a2代入,得
化简后得,
解得 ,
即 .
选(B). 【思路分析】(二)
令a=1,则b2=c2-1,
= 2b2 = 2(c2-1),
|F1F2 | = 2c.
由 ,
解得 ,
即 ,
选(B).
例7 已知三棱锥A-BCD中, E、F、G、H分别为AB、AC、CD、BD的中点,则截面EFGH把三棱锥A-BCD分成两部分的体积比为( )
(A) 1∶ 1
(B) 1∶ 2
(C) 2∶ 3
(D) 3∶ 4
使AD⊥平面BCD,且BC⊥CD.
设BC = CD = AD = 2,则
,选(A). 【思路分析】(一). . . 【思路分析】(二)
使三棱锥变为各条棱长皆相等的正四面体,认真观察后会发现,被截面所截的两个多面体是完全相同的,所以它们的体积比为1∶1,选(A).
3.强化估值法的训练 例8 已知α、β都是锐角, 且 ,
, 则α+β的值等于( )
(A) (B)
(C) 或 (D) 或
画出单位圆, 由 ,
及 ,α、β
为锐角, 可大致确定出
α、β及 终边所在的
位置.
由图,显然α+β≠ ,
也不会两解,所以选(B).
【思路分析】
画出单位圆, 由 ,
及 ,α、β
为锐角, 可大致确定出
α、β及 终边所在的
位置.
由图,显然α+β≠ ,
也不会两解,所以选(B).
【思路分析】 例9 把复数1+i 对应的向量按顺时针方向旋转 ,所得到的向量对应的复数是( )
(A)
(B)
(C)
(D) 【思路分析】(一)
进行两个实部相乘,得 ,可将 (A) (D) 排除,再进行 i 与 相乘,得 i ,又将 (C) 排除,所以选 (B).
例9 把复数1+i 对应的向量按顺时针方向旋转 ,所得到的向量对应的复数是( )
(A)
(B)
(C)
(D) 【思路分析】(一)
进行两个实部相乘,得 ,可将 (A) (D) 排除,再进行 i 与 相乘,得 i ,又将 (C) 排除,所以选 (B).
【思路分析】(二)
画出复平面,作出向量1+i,再按顺时针方向旋转 , 得出向量即为所求。
z在第Ⅳ象限,
排除(A)(D).
虚部绝对值较
大,又排除(C) 而选
择(B).
4.适当进行新题型的训练
例10 如图, 四棱锥P-ABCD 的底面ABCD是一个正方形,PD⊥底面ABCD,则这个四棱锥的五个面中,互相垂直的面共有( )
(A) 3 对
(B) 4 对
(C) 5 对
(D) 6 对
【思路分析】
(1) 与底面ABCD垂直的有两个平面,它们是面PAD和面PDC.
(2) 与面PAD垂直的
还有面PAB和面PDC.
(3) 与面PDC垂直的
还有面PBC.
答案(C). 例11 已知三个函数y1,y2,y3以及对应的函数图象C1,C2,C3.将C1向左平移2个单位得到C2,将C2关于原点对称得到C3,若三个函数解析式从以下三式中选取: ,
, , 则 y1=_______________,
y2=_______________, y3= ______________. 【思路分析】
变换的顺序与方法是确定的.
第一次变换
第二次变换 观察三个解析式的特点,尤其是x的符号特点,先确定出y3,然后再确定y1和y2,最后进行验证.
例12 原市话资费为每3分钟0.18元,现调整为前3分钟资费为0.22元,超过3分钟,每分钟按0.11元计费,与调整前相比,一次通话提价的百分比( )
(A) 不会高于70%
(B) 会高于70%而不会高于90%
(C) 不会低于10%
(D) 高于30%而低于100%
特殊值排除.
通话4分钟时,
原话费:0.18×2 = 0.36
现话费:0.22+0.11 = 0.33 提价为负值
排除 (C) (D)
通话30分钟时
原话费:0.18×10 = 1.80
现话费:0.22+0.11×27 = 3.19
排除 (A) 而选 (B) . 【思路分析】(一)【思路分析】 (二)
可表示为:
所以提价 . 解好中等解答题的对策 例1 已知函数
(Ⅰ)求f(x)的最小正周期和值域;
(Ⅱ)求f(x)的单调增区间.
解:由于 (Ⅰ)易知周期T=?,值域为[-3,5]. 例2 已知△ABC的三个内角A,B,C 满足:
A+C=2B,
求 的值. 解: 由A+C=2B及A+B+C=180°,
知 B=60°,A+C=120°.
因为 ,
所以 .
从而得 . 例3 解关于x的不等式
(其中a>0,且a≠1).
解:因为 ,=故原不等式即,.设 ,则t≥0,
且 .
于是,原不等式可化为 ,
即 .
解之,得 . 当a>1时,得 ,
此时 . 综上,当a>1时,原不等式的解集是
,
当0 .
一、高考特点与能力要求 1.考查的内容既全面又突出重点.
2.不刻意追求单纯的记忆,突出 知识间的综合.
3.在熟练掌握基础知识的前提下,突出考查能力.
(1)通过考查数学思想和方法,突出考查能力.
(2)通过对解答速度的要求,突出考查能力.
(3)通过新题型,突出考查能力.
二、复习方法与复习建议 1.强化数形结合思想的训练
2.强化特殊化思想的训练
3.强化估值法的训练
4.适当进行新题型的训练
1.强化数形结合思想的训练
例1 函数y=ax3+
bx2+cx+d的图象如图
所示,其中|x1|> |x2|,则
( )
例1 函数y=ax3+
bx2+cx+d的图象如图
所示,其中|x1|> |x2|,则
( )
【思路分析】
由图得f (0) = 0,则d=0.
∴ f (x) = ax3+bx2+cx+d
= ax (x-x1 ) ( x-x2 )
当x>x2时,由图得
f (x)>0,x > 0,
x-x1>0,
x-x2> 0,
由此得 a>0.
又 y = ax (x-x1)(x-x2)
=ax3-a (x1+x2 )x2+ax1x2x
∴ b =-a( x1+x2),c= ax1x2
由于,| x1| > |x2|, 且x1 <0, x2 >0,
∴ x1+x2<0,x1x2<0,
又 a>0,
由此可得 b>0,c<0.
选(B) 例2 函数y=logax在x∈[2,+∞)上恒有| y |>1,则a的取值范围是( )
(A)
(B)
(C)
(D)或或 【思路分析】
令x = 2,|y | = 1,求出a = 2 或a = .
在同一坐标系内画出y = 和
的图象. 【思路分析】
令x = 2,|y | = 1,求出a = 2 或a = .
在同一坐标系内画出y = 和
的图象. 例3 复数 的辐角主值是 _________ . 【思路分析】
例3 复数 的辐角主值是 _________ . 【思路分析】
例4 已知两点A(-2,0),B(0,2),
点C是圆x2+y2-2x=0上的任意一点,则△ABC面积的最小值是( )
(A) (B)
(C) (D) 例4 已知两点A(-2,0),B(0,2),
点C是圆x2+y2-2x=0上的任意一点,则△ABC面积的最小值是( )
(A) (B)
(C) (D) 2.强化特殊化思想的训练
例5 已知函数 f (x) 对任意实数 x 都有 f (3-x) = f (2+x),它的一个单调递增区间是
[1, 2],则函数y = f (1-x) 在 ( )
(A) [-4,-3]上单调递增,[-2,-1]上单调递减
(B) [-3,-2]上单调递增,[-1, 0 ]上单调递减
(C) [-4,-3]上单调递减,[-2,-1]上单调递增
(D) [-3,-2]上单调递减,[-1, 0]上单调递增
【思路分析】
由f (3-x)=f (2+x)得y = f (x)的图象的对称轴为 .
又 f (x) 在 [1, 2] 上单调递增,
可令
则
.从图中可直观得到正确答案 (B). 例6 已知F1、F2是双曲线 (a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线的左支交于A、B两点,若△ABF2为正三角形, 那么该双曲线的离心率为( )
(A) (B) (C) 2 (D) 3【思路分析】(一)
,
由ABF2为正三角形得
即
将b2=c2-a2代入,得
化简后得,
解得 ,
即 .
选(B). 【思路分析】(二)
令a=1,则b2=c2-1,
= 2b2 = 2(c2-1),
|F1F2 | = 2c.
由 ,
解得 ,
即 ,
选(B).
例7 已知三棱锥A-BCD中, E、F、G、H分别为AB、AC、CD、BD的中点,则截面EFGH把三棱锥A-BCD分成两部分的体积比为( )
(A) 1∶ 1
(B) 1∶ 2
(C) 2∶ 3
(D) 3∶ 4
使AD⊥平面BCD,且BC⊥CD.
设BC = CD = AD = 2,则
,选(A). 【思路分析】(一). . . 【思路分析】(二)
使三棱锥变为各条棱长皆相等的正四面体,认真观察后会发现,被截面所截的两个多面体是完全相同的,所以它们的体积比为1∶1,选(A).
3.强化估值法的训练 例8 已知α、β都是锐角, 且 ,
, 则α+β的值等于( )
(A) (B)
(C) 或 (D) 或
画出单位圆, 由 ,
及 ,α、β
为锐角, 可大致确定出
α、β及 终边所在的
位置.
由图,显然α+β≠ ,
也不会两解,所以选(B).
【思路分析】
画出单位圆, 由 ,
及 ,α、β
为锐角, 可大致确定出
α、β及 终边所在的
位置.
由图,显然α+β≠ ,
也不会两解,所以选(B).
【思路分析】 例9 把复数1+i 对应的向量按顺时针方向旋转 ,所得到的向量对应的复数是( )
(A)
(B)
(C)
(D) 【思路分析】(一)
进行两个实部相乘,得 ,可将 (A) (D) 排除,再进行 i 与 相乘,得 i ,又将 (C) 排除,所以选 (B).
例9 把复数1+i 对应的向量按顺时针方向旋转 ,所得到的向量对应的复数是( )
(A)
(B)
(C)
(D) 【思路分析】(一)
进行两个实部相乘,得 ,可将 (A) (D) 排除,再进行 i 与 相乘,得 i ,又将 (C) 排除,所以选 (B).
【思路分析】(二)
画出复平面,作出向量1+i,再按顺时针方向旋转 , 得出向量即为所求。
z在第Ⅳ象限,
排除(A)(D).
虚部绝对值较
大,又排除(C) 而选
择(B).
4.适当进行新题型的训练
例10 如图, 四棱锥P-ABCD 的底面ABCD是一个正方形,PD⊥底面ABCD,则这个四棱锥的五个面中,互相垂直的面共有( )
(A) 3 对
(B) 4 对
(C) 5 对
(D) 6 对
【思路分析】
(1) 与底面ABCD垂直的有两个平面,它们是面PAD和面PDC.
(2) 与面PAD垂直的
还有面PAB和面PDC.
(3) 与面PDC垂直的
还有面PBC.
答案(C). 例11 已知三个函数y1,y2,y3以及对应的函数图象C1,C2,C3.将C1向左平移2个单位得到C2,将C2关于原点对称得到C3,若三个函数解析式从以下三式中选取: ,
, , 则 y1=_______________,
y2=_______________, y3= ______________. 【思路分析】
变换的顺序与方法是确定的.
第一次变换
第二次变换 观察三个解析式的特点,尤其是x的符号特点,先确定出y3,然后再确定y1和y2,最后进行验证.
例12 原市话资费为每3分钟0.18元,现调整为前3分钟资费为0.22元,超过3分钟,每分钟按0.11元计费,与调整前相比,一次通话提价的百分比( )
(A) 不会高于70%
(B) 会高于70%而不会高于90%
(C) 不会低于10%
(D) 高于30%而低于100%
特殊值排除.
通话4分钟时,
原话费:0.18×2 = 0.36
现话费:0.22+0.11 = 0.33 提价为负值
排除 (C) (D)
通话30分钟时
原话费:0.18×10 = 1.80
现话费:0.22+0.11×27 = 3.19
排除 (A) 而选 (B) . 【思路分析】(一)【思路分析】 (二)
可表示为:
所以提价 . 解好中等解答题的对策 例1 已知函数
(Ⅰ)求f(x)的最小正周期和值域;
(Ⅱ)求f(x)的单调增区间.
解:由于 (Ⅰ)易知周期T=?,值域为[-3,5]. 例2 已知△ABC的三个内角A,B,C 满足:
A+C=2B,
求 的值. 解: 由A+C=2B及A+B+C=180°,
知 B=60°,A+C=120°.
因为 ,
所以 .
从而得 . 例3 解关于x的不等式
(其中a>0,且a≠1).
解:因为 ,=故原不等式即,.设 ,则t≥0,
且 .
于是,原不等式可化为 ,
即 .
解之,得 . 当a>1时,得 ,
此时 . 综上,当a>1时,原不等式的解集是
,
当0
同课章节目录
