选择题的解法[上学期]
图片预览








文档简介
课件26张PPT。高考选择题解法制作: 寻甸民族中学 夏军 解答高考数学选择题既要求准确破解,又要快速选择,正如《考试说明》中明确指出的,应“多一点想的,少一点算的” 该算不算,巧判断. 因而,在解答时应该突出一个"选"字,尽量减少书写解题过程,在对照选支的同时,多方考虑间接解法,依据题目的具体特点,灵活、巧妙、快速地选择巧法,以便快速智取.
高考中的数学选择题一般是容易题或中档题,个别题属于较难题,当中的大多数题的解答可用特殊的方法快速选择. 例如:估值选择法、特值检验法、顺推破解法、数形结合法、
特征分析法、逆推验证法、提炼公式法等都是常用的解法. 解题时还应特别注意:数学选择题的四个选择支中有且仅有一个是正确的,因而在求解时对照选支就显得非常重要,它是快速选择、正确作答的基本前提.
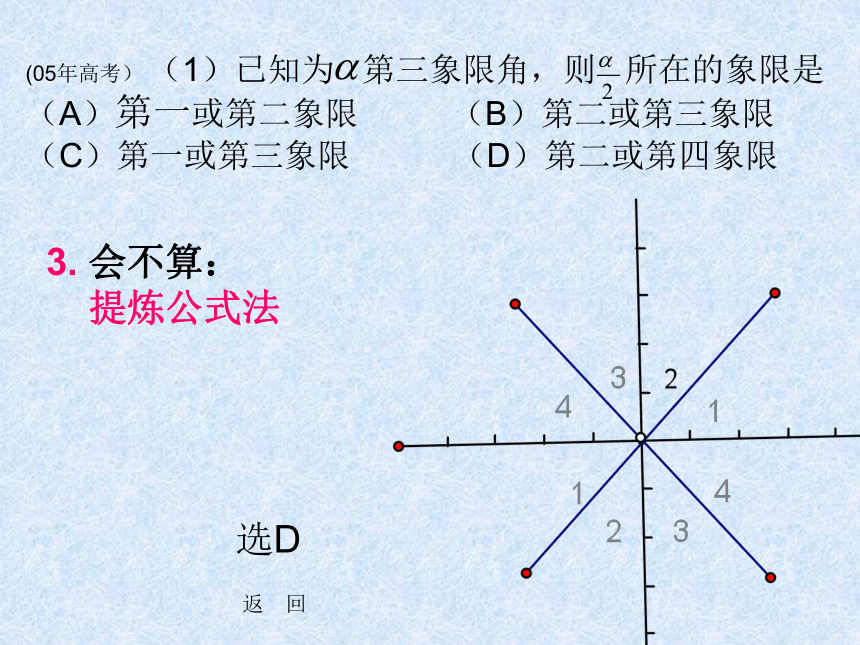
(05年高考) (1)已知 为第三象限角,则 所在的象限是
(A)第一或第二象限 (B)第二或第三象限
(C)第一或第三象限 (D)第二或第四象限①会算:顺推破解法
K取奇数时在第四象限。 K取偶数时在第二象限。 选D (05年高考) (1)已知 为第三象限角,则 所在的象限是
(A) 第一或第二象限 (B)第二或第三象限
(C)第一或第三象限 (D)第二或第四象限 在范围内取一个正角(225度)一个负角(-135)度,除以2得112.5度或-65度。
选D②会少算:特殊值法。(05年高考) (1)已知为 第三象限角,则 所在的象限是
(A)第一或第二象限 (B)第二或第三象限
(C)第一或第三象限 (D)第二或第四象限选D 3. 会不算:
提炼公式法返 回2、若sinθcosθ>0,则θ在 A、第一、二象限 B、第一、三象限 C、第一、四象限 D、第二、四象限①会算:顺推破解法
当k为偶数时,在θ第一象限;当为奇数时,在θ第三象限。故选B。
②会少算:特殊值法。知应排除A、C、D,故选B
③会不算:估值选择法
由sinθcosθ>0,知sinθ与cosθ同号,故选B。2、若sinθcosθ>0,则θ在 A、第一、二象限 B、第一、三象限 C、第一、四象限 D、第二、四象限当 时可排除A、B选项,矛盾故选D不算:特值检验法4、过点A(1,-1)、B(-1,1)且圆心在直线 x + y -2 = 0上的圆的方程是
A、(x-3)2 + (y+1)2 = 4
B、(x+3)2 + (y-1)2 = 4
C、(x-1)2 + (y-1)2 = 4
D、(x+1)2 + (y+1)2 = 4①会算:顺推破解法
因圆心在直线x+y-2=0上,设圆心为(a,2-a),又A、B在圆上,故解得a=1,圆心(1,1),故选C.②会少算:代入验证法
由选项B、D的圆心不在直线x+y-2=0 ,排除B、D;又选项A的圆不过点B,又排除A,故选C。4、过点A(1,-1)、B(-1,1)且圆心在直线 x + y -2 = 0上的圆的方程是
A、(x-3)2 + (y+1)2 = 4
B、(x+3)2 + (y-1)2 = 4
C、(x-1)2 + (y-1)2 = 4
D、(x+1)2 + (y+1)2 = 4③会不算:估值选择法
由选项知,只要估算出圆心所在象限即可。显然圆心应在线段AB的垂直平分线(即一、三象限的角平分线)上,又在直线x+y-2=0上,画草图知,交点(即圆心)在第一象限内,故选C。
4、过点A(1,-1)、B(-1,1)且圆心在直线 x + y -2 = 0上的圆的方程是
A、(x-3)2 + (y+1)2 = 4
B、(x+3)2 + (y-1)2 = 4
C、(x-1)2 + (y-1)2 = 4
D、(x+1)2 + (y+1)2 = 45、设{an}是递增等差数列,前三项和为12,前三项积为48,则它的首项是 A、1 B、2 C、4 D、 6 ①会算:直接法
设{an}的首项为a1,公差为d,
故选B。②会少算:性质法
因三项和为12,可设前三项分别为4-d,4,4+d,则4(4-d)(4+d)=48,
解得d=2(d=-2舍去),故首项为4-2=2,选B。③会不算:观察法
观察选项,2+4+6=12,2×4×6=48,故选B。5、设{an}是递增等差数列,前三项和为12,前三项积为48,则它的首项是 A、1 B、2 C、4 D、 6 6、若定义在区间(-1,0)内的函数f(x)= log 2 a(x +1) 满足f(x)>0, 则a的取值范围是 ①会算:直接法
∵-1<x<0 ,∴0<x+1<1,根据对数函数性质可得:0<2a<1,
6、若定义在区间(-1,0)内的函数f(x)= log 2 a(x +1) 满足f(x)>0, 则a的取值范围是 ③会不算:数形结合法
作出f(x)= log2a (x+1)
的图象,可得0<2a<1,故选A.
6、若定义在区间(-1,0)内的函数f(x)= log 2 a(x +1) 满足f(x)>0, 则a的取值范围是 7(05年辽宁 8)若钝角三角形三内角的度数成等差数列,且最大边与最小边长的比值为m,则m的范围是
(A) (B)
(C) (D)不算:数形结合法∵钝角三角形三内角的度数成等差数列,
∴其中一个角为60o,如图,直角三角形时, ,
所以钝角三角形时,有 ,故选B. 8湖北 7.若 ( )
A B. C. D. 解:∵sinα+cosα= ∈(1, ), ∴排除(A),(B),当α=时,tanα=1,sinα+cosα=, 这时
sinα+cosα≠tanα,∴选(C)对照选支9北京 4.从原点向圆 作两条切线,则该圆夹在两条切线间的劣弧长为( )
A.π B.2π C.4π D.6π 数形结合法将圆的方程配方得:
圆心在 半径为3,如图:
在图中 中, 从而得到,
即 可求
可求得劣弧长为.PQFpqOx 特殊图形法解得,正确答案为A 会算:顺推破解法数形结合法课堂小结1、解选择题首先要会算,其次要会少算,再次是会不算。会算是对基础知识、基本方法、基本技能有了一定的掌握,会不算只能在会算的基础上,根据实际情况灵活使用解题方法,才能达到的最高境界。2、正确、合理、迅速是解选择题的基本要求,只有在平时的训练中善于总结方法,才能在高考中达到这一要求。
高考中的数学选择题一般是容易题或中档题,个别题属于较难题,当中的大多数题的解答可用特殊的方法快速选择. 例如:估值选择法、特值检验法、顺推破解法、数形结合法、
特征分析法、逆推验证法、提炼公式法等都是常用的解法. 解题时还应特别注意:数学选择题的四个选择支中有且仅有一个是正确的,因而在求解时对照选支就显得非常重要,它是快速选择、正确作答的基本前提.
(05年高考) (1)已知 为第三象限角,则 所在的象限是
(A)第一或第二象限 (B)第二或第三象限
(C)第一或第三象限 (D)第二或第四象限①会算:顺推破解法
K取奇数时在第四象限。 K取偶数时在第二象限。 选D (05年高考) (1)已知 为第三象限角,则 所在的象限是
(A) 第一或第二象限 (B)第二或第三象限
(C)第一或第三象限 (D)第二或第四象限 在范围内取一个正角(225度)一个负角(-135)度,除以2得112.5度或-65度。
选D②会少算:特殊值法。(05年高考) (1)已知为 第三象限角,则 所在的象限是
(A)第一或第二象限 (B)第二或第三象限
(C)第一或第三象限 (D)第二或第四象限选D 3. 会不算:
提炼公式法返 回2、若sinθcosθ>0,则θ在 A、第一、二象限 B、第一、三象限 C、第一、四象限 D、第二、四象限①会算:顺推破解法
当k为偶数时,在θ第一象限;当为奇数时,在θ第三象限。故选B。
②会少算:特殊值法。知应排除A、C、D,故选B
③会不算:估值选择法
由sinθcosθ>0,知sinθ与cosθ同号,故选B。2、若sinθcosθ>0,则θ在 A、第一、二象限 B、第一、三象限 C、第一、四象限 D、第二、四象限当 时可排除A、B选项,矛盾故选D不算:特值检验法4、过点A(1,-1)、B(-1,1)且圆心在直线 x + y -2 = 0上的圆的方程是
A、(x-3)2 + (y+1)2 = 4
B、(x+3)2 + (y-1)2 = 4
C、(x-1)2 + (y-1)2 = 4
D、(x+1)2 + (y+1)2 = 4①会算:顺推破解法
因圆心在直线x+y-2=0上,设圆心为(a,2-a),又A、B在圆上,故解得a=1,圆心(1,1),故选C.②会少算:代入验证法
由选项B、D的圆心不在直线x+y-2=0 ,排除B、D;又选项A的圆不过点B,又排除A,故选C。4、过点A(1,-1)、B(-1,1)且圆心在直线 x + y -2 = 0上的圆的方程是
A、(x-3)2 + (y+1)2 = 4
B、(x+3)2 + (y-1)2 = 4
C、(x-1)2 + (y-1)2 = 4
D、(x+1)2 + (y+1)2 = 4③会不算:估值选择法
由选项知,只要估算出圆心所在象限即可。显然圆心应在线段AB的垂直平分线(即一、三象限的角平分线)上,又在直线x+y-2=0上,画草图知,交点(即圆心)在第一象限内,故选C。
4、过点A(1,-1)、B(-1,1)且圆心在直线 x + y -2 = 0上的圆的方程是
A、(x-3)2 + (y+1)2 = 4
B、(x+3)2 + (y-1)2 = 4
C、(x-1)2 + (y-1)2 = 4
D、(x+1)2 + (y+1)2 = 45、设{an}是递增等差数列,前三项和为12,前三项积为48,则它的首项是 A、1 B、2 C、4 D、 6 ①会算:直接法
设{an}的首项为a1,公差为d,
故选B。②会少算:性质法
因三项和为12,可设前三项分别为4-d,4,4+d,则4(4-d)(4+d)=48,
解得d=2(d=-2舍去),故首项为4-2=2,选B。③会不算:观察法
观察选项,2+4+6=12,2×4×6=48,故选B。5、设{an}是递增等差数列,前三项和为12,前三项积为48,则它的首项是 A、1 B、2 C、4 D、 6 6、若定义在区间(-1,0)内的函数f(x)= log 2 a(x +1) 满足f(x)>0, 则a的取值范围是 ①会算:直接法
∵-1<x<0 ,∴0<x+1<1,根据对数函数性质可得:0<2a<1,
6、若定义在区间(-1,0)内的函数f(x)= log 2 a(x +1) 满足f(x)>0, 则a的取值范围是 ③会不算:数形结合法
作出f(x)= log2a (x+1)
的图象,可得0<2a<1,故选A.
6、若定义在区间(-1,0)内的函数f(x)= log 2 a(x +1) 满足f(x)>0, 则a的取值范围是 7(05年辽宁 8)若钝角三角形三内角的度数成等差数列,且最大边与最小边长的比值为m,则m的范围是
(A) (B)
(C) (D)不算:数形结合法∵钝角三角形三内角的度数成等差数列,
∴其中一个角为60o,如图,直角三角形时, ,
所以钝角三角形时,有 ,故选B. 8湖北 7.若 ( )
A B. C. D. 解:∵sinα+cosα= ∈(1, ), ∴排除(A),(B),当α=时,tanα=1,sinα+cosα=, 这时
sinα+cosα≠tanα,∴选(C)对照选支9北京 4.从原点向圆 作两条切线,则该圆夹在两条切线间的劣弧长为( )
A.π B.2π C.4π D.6π 数形结合法将圆的方程配方得:
圆心在 半径为3,如图:
在图中 中, 从而得到,
即 可求
可求得劣弧长为.PQFpqOx 特殊图形法解得,正确答案为A 会算:顺推破解法数形结合法课堂小结1、解选择题首先要会算,其次要会少算,再次是会不算。会算是对基础知识、基本方法、基本技能有了一定的掌握,会不算只能在会算的基础上,根据实际情况灵活使用解题方法,才能达到的最高境界。2、正确、合理、迅速是解选择题的基本要求,只有在平时的训练中善于总结方法,才能在高考中达到这一要求。
同课章节目录
