人教版八年级数学下册第十八章练习题(附答案)
文档属性
| 名称 | 人教版八年级数学下册第十八章练习题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 71.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 12:48:59 | ||
图片预览

文档简介
人教版八年级数学下册第十八章练习题(附答案)
一、选择题
1.在平行四边形ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
2.如果等边三角形的边长为3,那么连接各边中点所成的三角形的周长为( )
A.9 B.6 C.3 D.
3.菱形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等C.对角线互相平分 D.对角互补
4.四边形ABCD中,AD∥BC.要判别四边形ABCD是平行四边形,还需满足条件( )
A.∠A+∠C=180° B.∠B+∠D=180° C.∠B+∠A=180° D.∠A+∠D=180°
5.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )
A.菱形 B.对角线互相垂直的四边形C.矩形 D.对角线相等的四边形
6.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是( )
A.12cm2 B.24cm2 C.48cm2 D.96cm2
7.矩形一个内角的平分线把矩形的一边分成3cm和5cm,则矩形的周长为( )
A.16cm B.22cm或26cm C.26cm D.以上都不对
8.如图,已知E,F分别为平行四边形ABCD边AD,AB上的两点,则图形中与△BEC的面积相等的三角形有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
10.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 cm2.
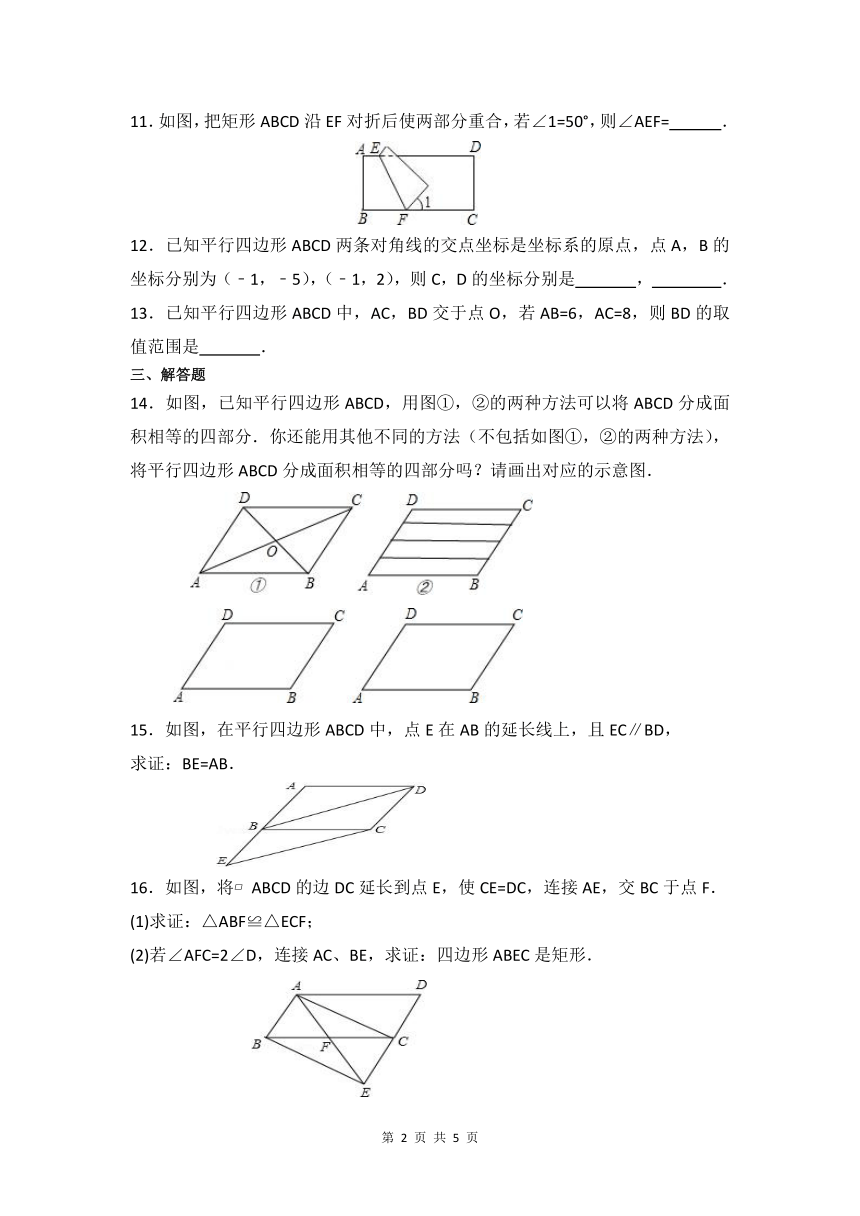
11.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF= .
12.已知平行四边形ABCD两条对角线的交点坐标是坐标系的原点,点A,B的坐标分别为(﹣1,﹣5),(﹣1,2),则C,D的坐标分别是 , .
13.已知平行四边形ABCD中,AC,BD交于点O,若AB=6,AC=8,则BD的取值范围是 .
三、解答题
14.如图,已知平行四边形ABCD,用图①,②的两种方法可以将ABCD分成面积相等的四部分.你还能用其他不同的方法(不包括如图①,②的两种方法),将平行四边形ABCD分成面积相等的四部分吗?请画出对应的示意图.
15.如图,在平行四边形ABCD中,点E在AB的延长线上,且EC∥BD,
求证:BE=AB.
16.如图,将 ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
17.已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证:四边形AFCE是菱形.
18.已知:如图,正方形ABCD中,E为CD边上一点,F为BC边延长线上一点,CE=CF.
(1)观察猜想BE和DF的大小关系,并证明你的猜想;
(2)若∠BEC=60°,求∠EFD的度数.
答 案
1.B.2.D.3.A.4.D.5.D.6.B.7.B.8.B.9.对角线相等.
10.8.11.115°.12.(1,5)(1,﹣2)13.4<BD<20.
14.解:
15.证明:∵ABCD是平行四边形,
∴AB∥CD,即BE∥CD,
又∵EC∥BD,∴四边形BECD是平行四边形.
∴BE=CD.∴BE=AB.
16.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,
∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,∴△ABF≌△ECF(AAS).
(2)∵AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,
∴FA=FB,∴FA=FE=FB=FC,
∴AE=BC,∴四边形ABEC是矩形.
17.证明:方法一:∵AE∥FC.
∴∠EAC=∠FCA.
∵在△AOE与△COF中,,
∴△AOE≌△COF(ASA).∴EO=FO,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,∴四边形AFCE为菱形;
方法二:同方法一,证得△AOE≌△COF.
∴AE=CF.∴四边形AFCE是平行四边形.
又∵EF是AC的垂直平分线,∴EA=EC,
∴四边形AFCE是菱形;
18.解:(1)BE=DF.理由如下:
如图,∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCF=90°,
又∵CE=CF,
∴△BCE≌△DCF,
∴BE=DF;
(2)∵△BCE≌△DCF,∠BEC=60°,
∴∠DFC=∠BEC=60°,
∵∠DCF=90°,CE=CF,
∴∠CFE=45°,
∴∠EFD=∠DFC﹣∠CFE=15°.
一、选择题
1.在平行四边形ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
2.如果等边三角形的边长为3,那么连接各边中点所成的三角形的周长为( )
A.9 B.6 C.3 D.
3.菱形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等C.对角线互相平分 D.对角互补
4.四边形ABCD中,AD∥BC.要判别四边形ABCD是平行四边形,还需满足条件( )
A.∠A+∠C=180° B.∠B+∠D=180° C.∠B+∠A=180° D.∠A+∠D=180°
5.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )
A.菱形 B.对角线互相垂直的四边形C.矩形 D.对角线相等的四边形
6.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是( )
A.12cm2 B.24cm2 C.48cm2 D.96cm2
7.矩形一个内角的平分线把矩形的一边分成3cm和5cm,则矩形的周长为( )
A.16cm B.22cm或26cm C.26cm D.以上都不对
8.如图,已知E,F分别为平行四边形ABCD边AD,AB上的两点,则图形中与△BEC的面积相等的三角形有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
10.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 cm2.
11.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF= .
12.已知平行四边形ABCD两条对角线的交点坐标是坐标系的原点,点A,B的坐标分别为(﹣1,﹣5),(﹣1,2),则C,D的坐标分别是 , .
13.已知平行四边形ABCD中,AC,BD交于点O,若AB=6,AC=8,则BD的取值范围是 .
三、解答题
14.如图,已知平行四边形ABCD,用图①,②的两种方法可以将ABCD分成面积相等的四部分.你还能用其他不同的方法(不包括如图①,②的两种方法),将平行四边形ABCD分成面积相等的四部分吗?请画出对应的示意图.
15.如图,在平行四边形ABCD中,点E在AB的延长线上,且EC∥BD,
求证:BE=AB.
16.如图,将 ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
17.已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证:四边形AFCE是菱形.
18.已知:如图,正方形ABCD中,E为CD边上一点,F为BC边延长线上一点,CE=CF.
(1)观察猜想BE和DF的大小关系,并证明你的猜想;
(2)若∠BEC=60°,求∠EFD的度数.
答 案
1.B.2.D.3.A.4.D.5.D.6.B.7.B.8.B.9.对角线相等.
10.8.11.115°.12.(1,5)(1,﹣2)13.4<BD<20.
14.解:
15.证明:∵ABCD是平行四边形,
∴AB∥CD,即BE∥CD,
又∵EC∥BD,∴四边形BECD是平行四边形.
∴BE=CD.∴BE=AB.
16.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,
∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,∴△ABF≌△ECF(AAS).
(2)∵AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,
∴FA=FB,∴FA=FE=FB=FC,
∴AE=BC,∴四边形ABEC是矩形.
17.证明:方法一:∵AE∥FC.
∴∠EAC=∠FCA.
∵在△AOE与△COF中,,
∴△AOE≌△COF(ASA).∴EO=FO,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,∴四边形AFCE为菱形;
方法二:同方法一,证得△AOE≌△COF.
∴AE=CF.∴四边形AFCE是平行四边形.
又∵EF是AC的垂直平分线,∴EA=EC,
∴四边形AFCE是菱形;
18.解:(1)BE=DF.理由如下:
如图,∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCF=90°,
又∵CE=CF,
∴△BCE≌△DCF,
∴BE=DF;
(2)∵△BCE≌△DCF,∠BEC=60°,
∴∠DFC=∠BEC=60°,
∵∠DCF=90°,CE=CF,
∴∠CFE=45°,
∴∠EFD=∠DFC﹣∠CFE=15°.
