第五单元_第01课时_ 鸽巢问题(一) (教学课件)-六年级数学下册人教版(共30张PPT)
文档属性
| 名称 | 第五单元_第01课时_ 鸽巢问题(一) (教学课件)-六年级数学下册人教版(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 15:43:55 | ||
图片预览






文档简介
(共30张PPT)
小学数学·六年级(下)·RJ
第1课时 鸽巢问题(一)
经历“鸽巢原理”的探究过程,会运用“鸽巢原理”解决一些简单的实际问题。
初步了解“鸽巢问题”的基本形式,理解关键词语“总有”和“至少”的含义。
体会“鸽巢问题”的广泛应用,培养探究意识。
经历“鸽巢原理”的探究过程,初步理解“鸽巢原理”的含义。
掌握运用“鸽巢原理”解决简单的实际问题的方法。
增强对逻辑推理、模型思想的体验,提高学习数学的兴趣和应用意识。
游戏名称:扑克牌游戏。
游戏道具:一副扑克牌,取出大小王,剩52张。
游戏方法:5名同学每人随意抽出一张扑克牌。
至少有2张牌是同花色的。相信吗?
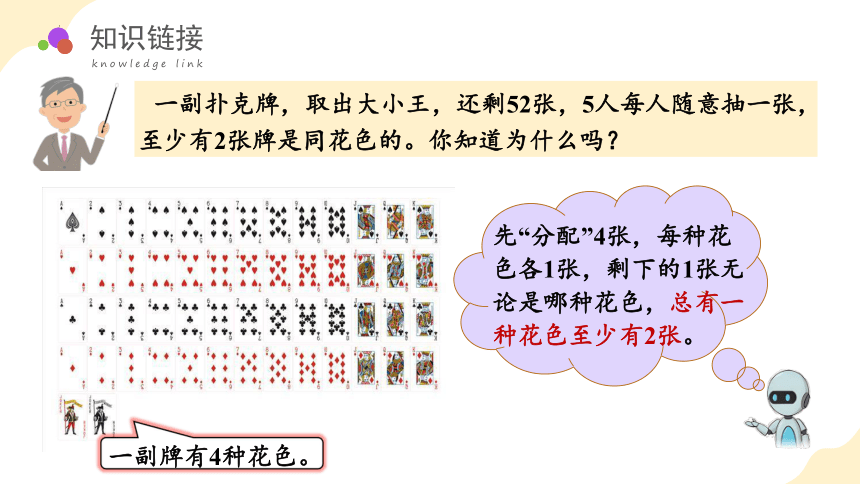
一副扑克牌,取出大小王,还剩52张,5人每人随意抽一张,至少有2张牌是同花色的。你知道为什么吗?
一副牌有4种花色。
先“分配”4张,每种花色各1张,剩下的1张无论是哪种花色,总有一种花色至少有2张。
初步理解“鸽巢原理”的含义。
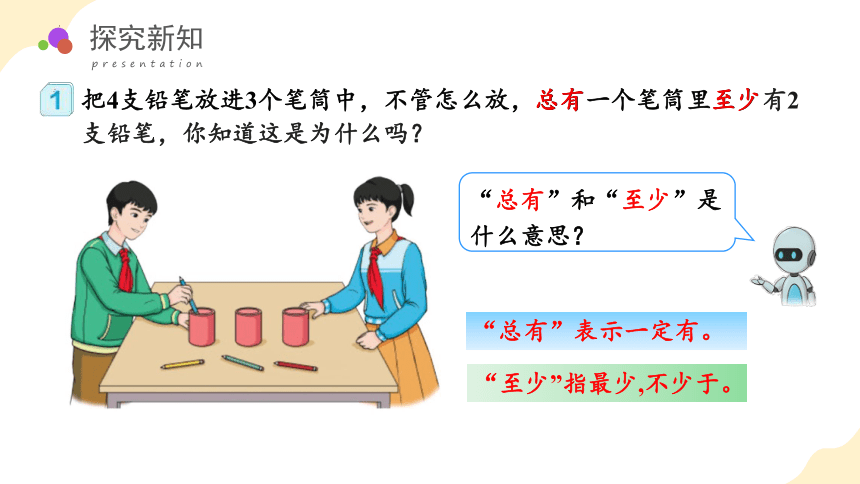
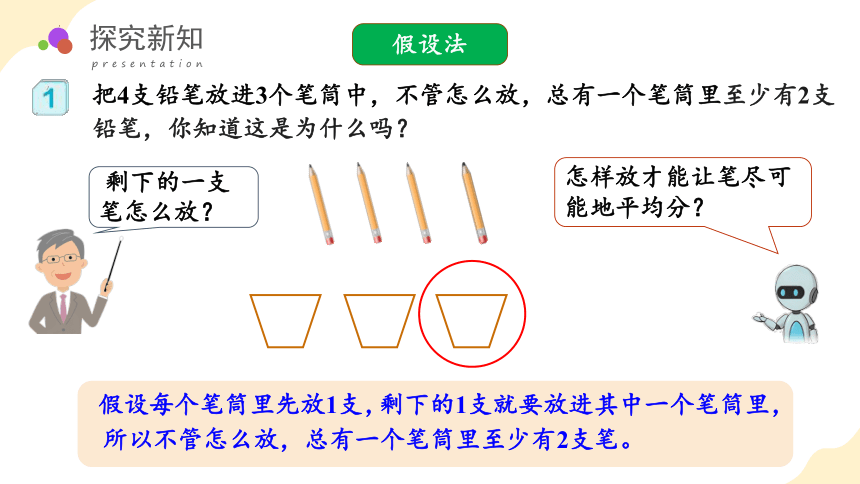
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔,你知道这是为什么吗?
“总有”和“至少”是什么意思?
总有
至少
“总有”表示一定有。
“至少”指最少,不少于。
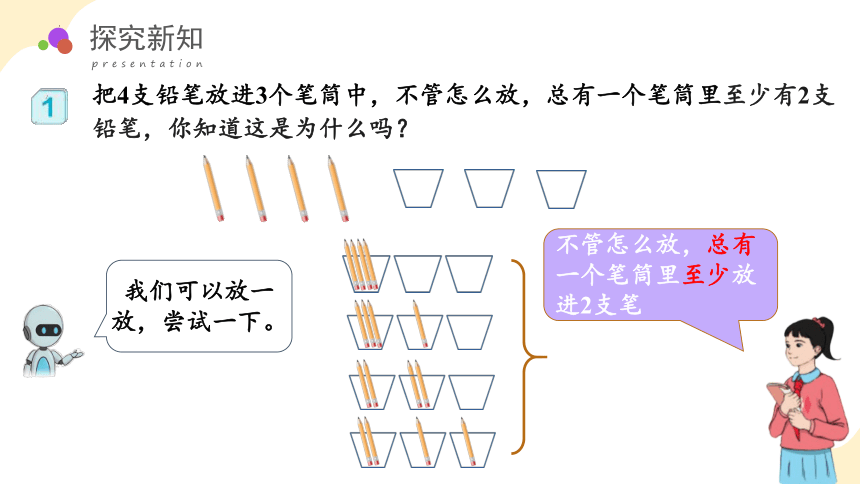
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔,你知道这是为什么吗?
我们可以放一放,尝试一下。
不管怎么放,总有一个笔筒里至少放进2支笔
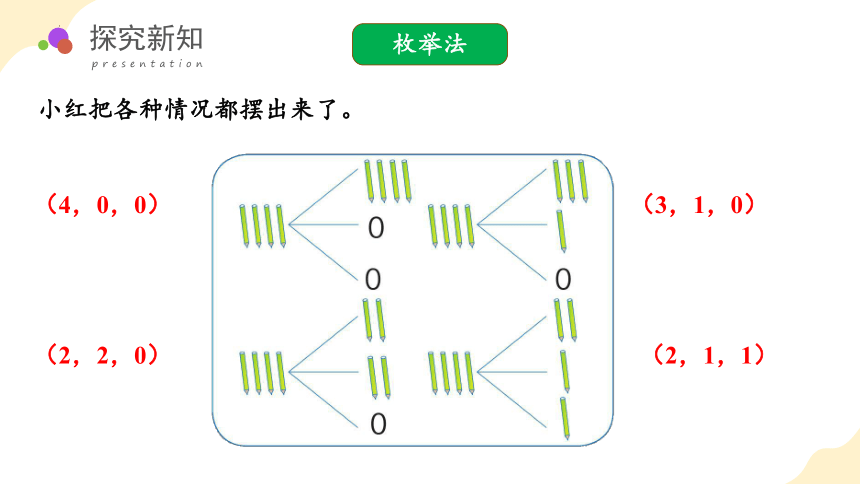
小红把各种情况都摆出来了。
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
枚举法
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔,你知道这是为什么吗?
剩下的1支就要放进其中一个笔筒里,
假设每个笔筒里先放1支,
所以不管怎么放,总有一个笔筒里至少有2支笔。
怎样放才能让笔尽可能地平均分?
剩下的一支 笔怎么放?
假设法
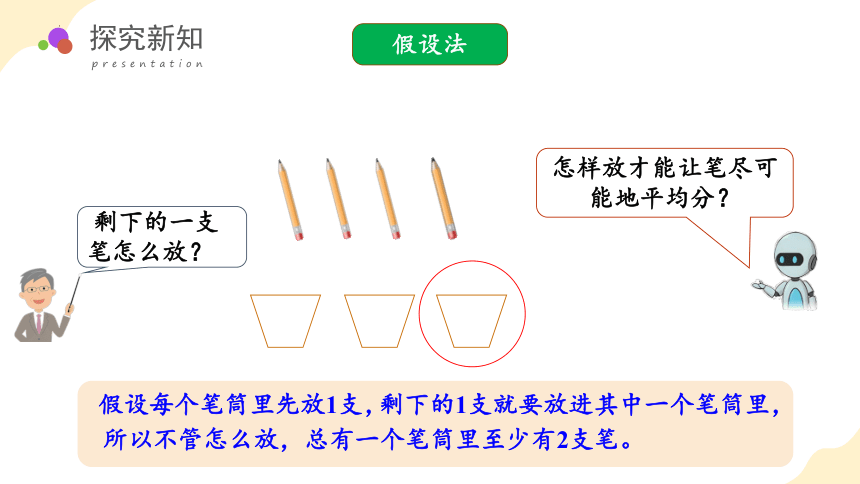
剩下的1支就要放进其中一个笔筒里,
假设每个笔筒里先放1支,
所以不管怎么放,总有一个笔筒里至少有2支笔。
怎样放才能让笔尽可能地平均分?
剩下的一支 笔怎么放?
假设法
掌握运用“鸽巢原理”解决简单的实际问题的方法。
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
你是怎么想的?小组讨论探究。
物体数量较多时,使用“枚举法”分析容易出现错漏。
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
我随便放放看,一个抽屉1本,一个抽屉2本,一个抽屉4本。
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以······
两种放法都有一个抽屉放了3本或多于3本,所以······
先把物体尽量平均分,把7本书分成3份
7÷3=2(本)······1(本)
多出的1本放到其中一个抽屉中
2+1=3(本)
总有一个抽屉至少有3本
(2)如果有8本书会怎么样呢?
8÷3=2(本)······2(本)
2+1=3(本)
总有一个抽屉至少有3本。
(3)如果有10本书呢?
10÷3=3(本)······1(本)
3+1=4(本)
总有一个抽屉至少有4本。
触类旁通
7÷3=2(本)……1(本)
2+1=3(本)
8÷3=2(本)……2(本)
2+1=3(本)
10÷3=3(本)……1(本)
3+1=4(本)
规律总结
观察左边的算式,思考如何求总有一个抽屉至少放进几本书?
鸽巢原理
物体数÷抽屉数=商……余数
商+1=至少数
“鸽巢问题”也称为“抽屉问题”
达标练习,巩固成果
1. 随意找13位老师,他们中至少有2个人的属相相同。为什么?
因为属相一共共有12个,人数是13个比属相多1个,所以一定有2个人的属相相同。
13÷12=1······1
1+1=2
2. 5只鸽子飞进了3个鸽笼,总有1个鸽笼至少飞进了2只鸽子。为什么?
如果每个鸽笼飞进1只鸽子,最多能飞进3只鸽子,剩下的2只鸽子还要飞进戈隆,所以至少有2只鸽子需要飞进同一个鸽笼里。
5÷3=1(只)······2(只)
1+1=2(只)
3. 小明表演扑克牌“魔术”。一副扑克牌,取出大小王,还剩52张牌,9人每人随意抽1张,至少有3张牌是相同的花色。你理解这个扑克牌“魔术”的道理吗
一副扑克牌共54张,去掉两张王牌,剩下方块、红桃、梅花、黑桃四种花色各13张。我们把4种花色看成“4个鸽巢”,问题转化成把9张扑克牌放进“4个鸽巢”中。
9÷4=2······1
2+1=3
4. 张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于9环。为什么?
41÷5=8······1
8+1=9(环)
5. 给1个正方体木块的6个面分别涂上蓝、黄两种颜色,不论怎么涂至少有3个面涂的颜色相同。为什么?
把两种颜色看成两个抽屉,正方体的6个面看成分放的物体,至少3个面要涂上相同的颜色。
6÷2=3(个)
6. 给下面每个格子涂上红色或蓝色,至少有两列的涂色相同。为什么?
如果只涂两行的话,结论有什么变化呢?
表格共9列,红蓝两种颜色要涂三行,共有8种涂法,无论怎么涂,至少有2列的涂法相同。
9÷8=1······1
1+1=2
?
若只涂两行,共有4种涂法,无论怎么涂,至少有3列的涂法相同。
9÷4=2······1
2+1=3
至少有9枝花要插进同一个花瓶里。
至少有12枝花要插进同一个花瓶里。
100÷12=8(枝)······4(枝)
8+1=9(枝)
答:明明说的对。
他们俩谁说的对?
7. 把100枝花插进12个花瓶里。
8. 有3道测试题,每做对一题得3分,没做或做错不得分。全班45名同学至少有几名同学的得分是相同的?
答:全班45名同学至少有12名同学的得分是相同的。
45÷4 = 11(名)······1(名)
11 + 1= 12(名)
想一想,3道题总得分总共有( )种情况。
做对 没做/做错 得分
3题 0题 9分
2题 1题 6分
1题 2题 3分
0题 3题 0分
4
鸽巢原理(二):把多余kn个物体任意放进n个鸽巢中(k和n是非0自然数),那么一定有一个鸽巢里至少放进了( k +1)个物体。
鸽巢原理(一):把m个物体任意放进n个鸽巢中(m和n是非0自然数,且m>n),那么一定有一个 鸽巢里至少放进了2个物体。
这节课你有什么收获?
小学数学·六年级(下)·RJ
第1课时 鸽巢问题(一)
经历“鸽巢原理”的探究过程,会运用“鸽巢原理”解决一些简单的实际问题。
初步了解“鸽巢问题”的基本形式,理解关键词语“总有”和“至少”的含义。
体会“鸽巢问题”的广泛应用,培养探究意识。
经历“鸽巢原理”的探究过程,初步理解“鸽巢原理”的含义。
掌握运用“鸽巢原理”解决简单的实际问题的方法。
增强对逻辑推理、模型思想的体验,提高学习数学的兴趣和应用意识。
游戏名称:扑克牌游戏。
游戏道具:一副扑克牌,取出大小王,剩52张。
游戏方法:5名同学每人随意抽出一张扑克牌。
至少有2张牌是同花色的。相信吗?
一副扑克牌,取出大小王,还剩52张,5人每人随意抽一张,至少有2张牌是同花色的。你知道为什么吗?
一副牌有4种花色。
先“分配”4张,每种花色各1张,剩下的1张无论是哪种花色,总有一种花色至少有2张。
初步理解“鸽巢原理”的含义。
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔,你知道这是为什么吗?
“总有”和“至少”是什么意思?
总有
至少
“总有”表示一定有。
“至少”指最少,不少于。
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔,你知道这是为什么吗?
我们可以放一放,尝试一下。
不管怎么放,总有一个笔筒里至少放进2支笔
小红把各种情况都摆出来了。
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
枚举法
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔,你知道这是为什么吗?
剩下的1支就要放进其中一个笔筒里,
假设每个笔筒里先放1支,
所以不管怎么放,总有一个笔筒里至少有2支笔。
怎样放才能让笔尽可能地平均分?
剩下的一支 笔怎么放?
假设法
剩下的1支就要放进其中一个笔筒里,
假设每个笔筒里先放1支,
所以不管怎么放,总有一个笔筒里至少有2支笔。
怎样放才能让笔尽可能地平均分?
剩下的一支 笔怎么放?
假设法
掌握运用“鸽巢原理”解决简单的实际问题的方法。
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
你是怎么想的?小组讨论探究。
物体数量较多时,使用“枚举法”分析容易出现错漏。
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
我随便放放看,一个抽屉1本,一个抽屉2本,一个抽屉4本。
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以······
两种放法都有一个抽屉放了3本或多于3本,所以······
先把物体尽量平均分,把7本书分成3份
7÷3=2(本)······1(本)
多出的1本放到其中一个抽屉中
2+1=3(本)
总有一个抽屉至少有3本
(2)如果有8本书会怎么样呢?
8÷3=2(本)······2(本)
2+1=3(本)
总有一个抽屉至少有3本。
(3)如果有10本书呢?
10÷3=3(本)······1(本)
3+1=4(本)
总有一个抽屉至少有4本。
触类旁通
7÷3=2(本)……1(本)
2+1=3(本)
8÷3=2(本)……2(本)
2+1=3(本)
10÷3=3(本)……1(本)
3+1=4(本)
规律总结
观察左边的算式,思考如何求总有一个抽屉至少放进几本书?
鸽巢原理
物体数÷抽屉数=商……余数
商+1=至少数
“鸽巢问题”也称为“抽屉问题”
达标练习,巩固成果
1. 随意找13位老师,他们中至少有2个人的属相相同。为什么?
因为属相一共共有12个,人数是13个比属相多1个,所以一定有2个人的属相相同。
13÷12=1······1
1+1=2
2. 5只鸽子飞进了3个鸽笼,总有1个鸽笼至少飞进了2只鸽子。为什么?
如果每个鸽笼飞进1只鸽子,最多能飞进3只鸽子,剩下的2只鸽子还要飞进戈隆,所以至少有2只鸽子需要飞进同一个鸽笼里。
5÷3=1(只)······2(只)
1+1=2(只)
3. 小明表演扑克牌“魔术”。一副扑克牌,取出大小王,还剩52张牌,9人每人随意抽1张,至少有3张牌是相同的花色。你理解这个扑克牌“魔术”的道理吗
一副扑克牌共54张,去掉两张王牌,剩下方块、红桃、梅花、黑桃四种花色各13张。我们把4种花色看成“4个鸽巢”,问题转化成把9张扑克牌放进“4个鸽巢”中。
9÷4=2······1
2+1=3
4. 张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于9环。为什么?
41÷5=8······1
8+1=9(环)
5. 给1个正方体木块的6个面分别涂上蓝、黄两种颜色,不论怎么涂至少有3个面涂的颜色相同。为什么?
把两种颜色看成两个抽屉,正方体的6个面看成分放的物体,至少3个面要涂上相同的颜色。
6÷2=3(个)
6. 给下面每个格子涂上红色或蓝色,至少有两列的涂色相同。为什么?
如果只涂两行的话,结论有什么变化呢?
表格共9列,红蓝两种颜色要涂三行,共有8种涂法,无论怎么涂,至少有2列的涂法相同。
9÷8=1······1
1+1=2
?
若只涂两行,共有4种涂法,无论怎么涂,至少有3列的涂法相同。
9÷4=2······1
2+1=3
至少有9枝花要插进同一个花瓶里。
至少有12枝花要插进同一个花瓶里。
100÷12=8(枝)······4(枝)
8+1=9(枝)
答:明明说的对。
他们俩谁说的对?
7. 把100枝花插进12个花瓶里。
8. 有3道测试题,每做对一题得3分,没做或做错不得分。全班45名同学至少有几名同学的得分是相同的?
答:全班45名同学至少有12名同学的得分是相同的。
45÷4 = 11(名)······1(名)
11 + 1= 12(名)
想一想,3道题总得分总共有( )种情况。
做对 没做/做错 得分
3题 0题 9分
2题 1题 6分
1题 2题 3分
0题 3题 0分
4
鸽巢原理(二):把多余kn个物体任意放进n个鸽巢中(k和n是非0自然数),那么一定有一个鸽巢里至少放进了( k +1)个物体。
鸽巢原理(一):把m个物体任意放进n个鸽巢中(m和n是非0自然数,且m>n),那么一定有一个 鸽巢里至少放进了2个物体。
这节课你有什么收获?
