数学思想方法与高考数学复习[下学期]
图片预览











文档简介
课件46张PPT。数学思想方法与高考数学复习郭志龙福建仙游盖尾中学一.高考对数学思想方法的要求: 1. 《考试说明》的要求:一.高考对数学思想方法的要求: 1. 《考试说明》的要求: “数学科的命题,在考查基础知识的基础上,注重对数学思想和方法的考查,注重对数学能力的考查.”(《考试说明》(理科,2005年)第65页)
一.高考对数学思想方法的要求: 1. 《考试说明》的要求: “数学思想和方法是数学知识在更高层次的抽象和概括,它蕴涵在数学知识的发生、发展和应用的过程中,因此,对于数学思想和方法的考查要与数学知识的考查结合进行,通过数学知识的考查,反映考生对数学思想和方法理解和掌握的程度.考查时,要从学科整体意识和思想含义上立意,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度.”(《考试说明》(理科,2005年)第64页) 一.高考对数学思想方法的要求: 2.高考评价报告要求: 数学在培养和提高人的思维能力方面有着其他学科所不可替代的独特作用,这是因为数学不仅仅是一种重要的“工具”或者“方法”,更重要的是一种思维模式,表现为数学思想。高考数学科提出“以能力立意命题”,正是为了更好地考查数学思想,促进考生数学理性思维的发展。因此,要加强如何更好地考查数学思想的研究,特别是要研究试题解题过程的思维方法,注意考查不同思维方法的试题的协调和匹配,使考生的数学理性思维能力得到较全面的考查。”(《2005年普通高考数学科试题评价报告》(教育部考试中心))一.高考对数学思想方法的要求: 3.考试中心对教学与复习的建议: 在考试中心对数学复习的建议中指出:“数学思想方法较之数学基础知识有更高的层次.具有观念性的地位,如果说数学知识是数学内容,可用文字和符号来记录和描述,那么数学思想方法则是数学意识,只能领会、运用,属于思维的范畴,用以对数学问题的认识、处理和解决,中学数学思想和方法有数形结合思想,函数和方程思想,分类讨论思想,化归和转化思想”. “数学思想方法与数学基本方法常常在学习、掌握数学知识的同时获得,与此同时又应该领会它们在形成知识中的作用,到了复习阶段应该对数学思想方法和数学基本方法进行疏理、总结,逐个认识它们的本质特征、思维程序或者操作程序,逐步做到自觉地、灵活地施用于所要解决的问题
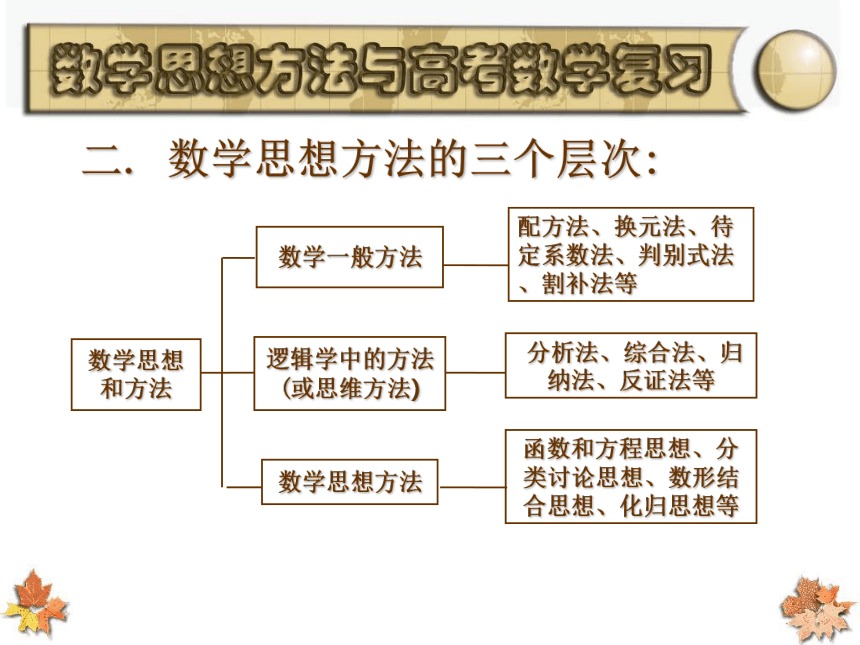
.近几年来,高考的每一道数学试题几乎都考虑到数学思想方法或数学基本方法的运用,目的也是加强这些方面的考查.同样,这些高考试题也成为检验数学知识,同时又是检验数学思想方法的良好素材,复习时可以有意识地加以运用.” 2005年对数学思想的考查二. 数学思想方法的三个层次: 三.用数学思想指导解题 三.用数学思想指导解题 1.函数和方程思想---用变量和函数来思考 著名数学家克莱因说“一般受教育者在数学课上应该学会的重要事情是用变量和函数来思考”. 三.用数学思想指导解题 1.函数和方程思想---用变量和函数来思考 用函数思想指导解题包括下面几个内容:
A 视代数式为函数,用函数的性质解题
B 用极值原理解题
C 构造函数解题
D 解函数问题的几个误区
A 视代数式为函数,用函数的性质解题 A 视代数式为函数,用函数的性质解题 例1 甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/小时)的平方成正比,且比例系数为b,固定部分为a元.
(1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域.
(2)为了使全程运输成本最小,汽车应以多大的速度行
驶?
(1997年,全国高考) A 视代数式为函数,用函数的性质解题 例2 已知曲线 与
有公共点,求实数 a 的取值范围.
B 用极值原理解题 例3 设a0为常数,且
(Ⅰ)证明对任意 , ;
(Ⅱ)假设对任意 ,有 an>an-1 ,求a0的取值范围。
(2003年,新课程卷) B 用极值原理解题 例4 设 ,
其中a为实数,n是给定的自然数,且 ,如果f(x)在
(-∞,1]上有意义,求a的取值范围.
(1990年, 全国高考) B 用极值原理解题 例5 定义在[-1,1]上的奇函数 f(x) 满足 f( 1 ) =1,且当
a,b∈[-1,1],a+b≠0时,有 >0.
(I) 证明当 时, f(x)≤ 3x ;
(II) 若 f(x)≤m2+2am+1对所有x∈[-1,1],a∈[-1,1] 上
恒成立,求m的取值范围. B 用极值原理解题 例6 对于在区间[m,n]上有意义的两个函数f(x)和g(x) ,
如果对任意的x∈[m,n] , 均有| f(x)- g(x)|≤1 , 则称
f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)
在[m,n]上是非接近的.
现有两个函数f1(x)= loga(x-3a)与 ,
给定区间[a+2,a+3].
(I)若f1 (x)与f2 (x)在给定区间[a+2,a+3]都有意义,求
实数a 的取值范围;
(II) 讨论 f1 (x)与 f2 (x)在给定区间[a+2,a+3]上是否是
接近的 C 构造函数解题 例7 设二次函数 f(x)=ax2+bx+c(a>0) .方程 f(x)-x=0的
两个根x1 , x2 满足0<x1<x2< .
(I) 当x∈(0, x1)时,证明x< f(x)<x1 ;
(II) 设函数f(x)的图像关于直线x=x0对称,
证明x0< .
(1997年, 全国高考) C 构造函数解题 例8 函数y= logax (a>0,a≠0)具有性质 ,
请举出一个符合条件的函数g(x)满足 ,其定
义域D满足 .
C 构造函数解题 例9 已知 i , m , n 是正整数,且1<i≤m<n.
(I) 证明 niAim< miAin;
(II) 证明 (1+m)n>(1+n)m .
(2001年,全国高考)
C 构造函数解题 例10 若a,b ∈ R,且a3-3a2+5a=1,b3-3b2+5b=5,求a+b.
D解函数问题的几个误区 Ⅰ)定义域和值域
例11 已知函数
(1)定义域是R ,求a的取值范围.
(2)值域是R ,求a的取值范围. D解函数问题的几个误区 Ⅱ)定义域和有意义
例12 已知函数 .
(1) 若此函数在(-∞,1]上有意义,求a的取值范围.
(2) 若此函数的定义域为(-∞,1] ,求a的取值范围. D解函数问题的几个误区 Ⅲ)值域和取值范围
例13 已知函数f(x)=3x2-(2m+6)x+m+3.
(1)若f(x)≥0恒成立,求m的取值范围.
(2) 若f(x)的值域为 ,求m的取值范围. D解函数问题的几个误区 Ⅳ)自身对称和互相对称
例14 设 f (x)定义在实数集R上.
(1)若f (1+x)= f (1-x) ,求f (x)图象的对称轴.
(2)若y=f(1+x)与y=f(1-x)的图像关于直线l 对称,
求直线l 的方程. D解函数问题的几个误区 V)恒成立,能成立,恰成立
例15 求实数a的范围:
(1) x2-ax-a>0恒成立.
(2) 存在x,使-x2+ax+a>0成立.
(3) 设a>1,不等式 的
解集为(1,+∞). . 2 数形结合思想---图形帮助解题 数与形是事物的两个方面,正是基于对数与形的抽象研究才产生了数学这门学科,才能使人们能够从不同侧面认识事物,数形结合思想就是要使抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维结合起来,华罗庚先生说过:“数与形本是两依倚,焉能分作两边飞. 数缺形时少直观, 形少数时难入微.”.数形结合思想是一种重要的解题思想,用这种思想指导,一些几何问题可以用代数方法来处理,例如解析几何,一些代数问题又可以用几何图形帮助解决,下面主要讲如何用图形帮助解题,这也是高考命题中主要考查的一个内容. 2 数形结合思想---图形帮助解题 A 利用图形求解的个数
例1 圆x2+2x+y2+4y-3=0到直线x+y+1=0的距离等于
的点共有( ).
(A)1个 (B)2个 (C)3个(D)4个
(1991年,全国高考) 用图形分析法求解的个数,实际上是转化为求图象交点的个数. 2 数形结合思想---图形帮助解题 求最值问题实际上是探讨图形的极端位置. B 利用图形求最值
例2 如果实数x,y满足等式(x-2)2+y2=3,那么 的最大值
是( ).
(A) (B) (C) (D)
(1990年,全国高考 ) 2 数形结合思想---图形帮助解题 C 利用图形求参数的范围 例3 橢圆 的焦点为F1 ,F2 ,点P为其上的动点,
当∠F1PF2为钝角时, 点P的横坐标的取值范围是___
(2002年,新课程卷) . 2 数形结合思想---图形帮助解题 C 利用图形求参数的范围 例4 已知两条直线l1:y=x,l2:ax-y=0,其中a为实数,当这两条
直线的夹角在 内变动时,a的变化范围是( ).
(0,1) (B)( (C )( (D)
(2000年,新课程卷) 2 数形结合思想---图形帮助解题 C 利用图形求参数的范围 求参数的范围实质上是弄清参数的几何意义,然后讨论参数所代表的几何意义的变化状态. 例5 设函数f (x ) = 若f (x0 )>1,则x0
的取值范围是( )。
(A) (-1,1) (B) (-1,+∞)
(C) (-∞,-2)∪(1,+∞) (D) (-∞,-1)∪(1,+∞)
(2003年,新课程卷) 2 数形结合思想---图形帮助解题 D 利用图形解不等式 例6 设函数 ,其中a>0,
⑴ 解不等式f(x)≤1;
⑵求a的取值范围,使f(x)在(0,+∞)上单调.
(2000年,全国高考) 2 数形结合思想---图形帮助解题 D 利用图形解不等式 用图形解不等式实际上是研究图象中符合条件的变量的变化范围. 例7 已知 i , m , n 是正整数,且1<i≤m<n.
(II) 证明 (1+m)n>(1+n)m .
(2001年,全国高考) 2 数形结合思想---图形帮助解题 E 利用图形求值 例8 求
的值.
(1992年,全国高考) 2 数形结合思想---图形帮助解题 E 利用图形求值 用图形分析法求值实际上是构造几何图形解题 . 例9???过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是( ).
(A) (B)
(C) (D)
(2000年, 新课程卷) 3分类讨论思想---分情况解决问题 例1? 设a为常数,函数f(x) =x2+|x-a|+1, x ∈ R.
(I) 讨论f(x)的奇偶性;
(II)求f(x)的最小值.
(2002年,全国高考)
3分类讨论思想---分情况解决问题 例2? 设a>0,求函数
的单调区间。
(2003年,新课程卷,理工)
3分类讨论思想---分情况解决问题 例3 某城市在中心广场建造一个花圃,花圃分为6个部分
(如图),现要栽种4种不同颜色的花,每部分栽种一种且相
邻部分不能栽种同样的颜色的花,不同的栽种方法有_____
种(以数字作答). (2003年,新课程卷)
3分类讨论思想---分情况解决问题 4 化归思想---化生题为熟题 4 化归思想---化生题为熟题 4 化归思想---化生题为熟题例2、如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90o,侧棱AA1=2 ,D,E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ ABD的重心G.
(Ⅰ)求A1B与平面ABD所成角的大小;
(结果用反三角函数表示)
(Ⅱ)求点A1到平面AED的距离。
(2003年新课程卷,全国卷) 4 化归思想---化生题为熟题例3 设对所有实数x,不等式
恒成立,求a的取值范围. Thank you
一.高考对数学思想方法的要求: 1. 《考试说明》的要求: “数学思想和方法是数学知识在更高层次的抽象和概括,它蕴涵在数学知识的发生、发展和应用的过程中,因此,对于数学思想和方法的考查要与数学知识的考查结合进行,通过数学知识的考查,反映考生对数学思想和方法理解和掌握的程度.考查时,要从学科整体意识和思想含义上立意,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度.”(《考试说明》(理科,2005年)第64页) 一.高考对数学思想方法的要求: 2.高考评价报告要求: 数学在培养和提高人的思维能力方面有着其他学科所不可替代的独特作用,这是因为数学不仅仅是一种重要的“工具”或者“方法”,更重要的是一种思维模式,表现为数学思想。高考数学科提出“以能力立意命题”,正是为了更好地考查数学思想,促进考生数学理性思维的发展。因此,要加强如何更好地考查数学思想的研究,特别是要研究试题解题过程的思维方法,注意考查不同思维方法的试题的协调和匹配,使考生的数学理性思维能力得到较全面的考查。”(《2005年普通高考数学科试题评价报告》(教育部考试中心))一.高考对数学思想方法的要求: 3.考试中心对教学与复习的建议: 在考试中心对数学复习的建议中指出:“数学思想方法较之数学基础知识有更高的层次.具有观念性的地位,如果说数学知识是数学内容,可用文字和符号来记录和描述,那么数学思想方法则是数学意识,只能领会、运用,属于思维的范畴,用以对数学问题的认识、处理和解决,中学数学思想和方法有数形结合思想,函数和方程思想,分类讨论思想,化归和转化思想”. “数学思想方法与数学基本方法常常在学习、掌握数学知识的同时获得,与此同时又应该领会它们在形成知识中的作用,到了复习阶段应该对数学思想方法和数学基本方法进行疏理、总结,逐个认识它们的本质特征、思维程序或者操作程序,逐步做到自觉地、灵活地施用于所要解决的问题
.近几年来,高考的每一道数学试题几乎都考虑到数学思想方法或数学基本方法的运用,目的也是加强这些方面的考查.同样,这些高考试题也成为检验数学知识,同时又是检验数学思想方法的良好素材,复习时可以有意识地加以运用.” 2005年对数学思想的考查二. 数学思想方法的三个层次: 三.用数学思想指导解题 三.用数学思想指导解题 1.函数和方程思想---用变量和函数来思考 著名数学家克莱因说“一般受教育者在数学课上应该学会的重要事情是用变量和函数来思考”. 三.用数学思想指导解题 1.函数和方程思想---用变量和函数来思考 用函数思想指导解题包括下面几个内容:
A 视代数式为函数,用函数的性质解题
B 用极值原理解题
C 构造函数解题
D 解函数问题的几个误区
A 视代数式为函数,用函数的性质解题 A 视代数式为函数,用函数的性质解题 例1 甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/小时)的平方成正比,且比例系数为b,固定部分为a元.
(1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域.
(2)为了使全程运输成本最小,汽车应以多大的速度行
驶?
(1997年,全国高考) A 视代数式为函数,用函数的性质解题 例2 已知曲线 与
有公共点,求实数 a 的取值范围.
B 用极值原理解题 例3 设a0为常数,且
(Ⅰ)证明对任意 , ;
(Ⅱ)假设对任意 ,有 an>an-1 ,求a0的取值范围。
(2003年,新课程卷) B 用极值原理解题 例4 设 ,
其中a为实数,n是给定的自然数,且 ,如果f(x)在
(-∞,1]上有意义,求a的取值范围.
(1990年, 全国高考) B 用极值原理解题 例5 定义在[-1,1]上的奇函数 f(x) 满足 f( 1 ) =1,且当
a,b∈[-1,1],a+b≠0时,有 >0.
(I) 证明当 时, f(x)≤ 3x ;
(II) 若 f(x)≤m2+2am+1对所有x∈[-1,1],a∈[-1,1] 上
恒成立,求m的取值范围. B 用极值原理解题 例6 对于在区间[m,n]上有意义的两个函数f(x)和g(x) ,
如果对任意的x∈[m,n] , 均有| f(x)- g(x)|≤1 , 则称
f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)
在[m,n]上是非接近的.
现有两个函数f1(x)= loga(x-3a)与 ,
给定区间[a+2,a+3].
(I)若f1 (x)与f2 (x)在给定区间[a+2,a+3]都有意义,求
实数a 的取值范围;
(II) 讨论 f1 (x)与 f2 (x)在给定区间[a+2,a+3]上是否是
接近的 C 构造函数解题 例7 设二次函数 f(x)=ax2+bx+c(a>0) .方程 f(x)-x=0的
两个根x1 , x2 满足0<x1<x2< .
(I) 当x∈(0, x1)时,证明x< f(x)<x1 ;
(II) 设函数f(x)的图像关于直线x=x0对称,
证明x0< .
(1997年, 全国高考) C 构造函数解题 例8 函数y= logax (a>0,a≠0)具有性质 ,
请举出一个符合条件的函数g(x)满足 ,其定
义域D满足 .
C 构造函数解题 例9 已知 i , m , n 是正整数,且1<i≤m<n.
(I) 证明 niAim< miAin;
(II) 证明 (1+m)n>(1+n)m .
(2001年,全国高考)
C 构造函数解题 例10 若a,b ∈ R,且a3-3a2+5a=1,b3-3b2+5b=5,求a+b.
D解函数问题的几个误区 Ⅰ)定义域和值域
例11 已知函数
(1)定义域是R ,求a的取值范围.
(2)值域是R ,求a的取值范围. D解函数问题的几个误区 Ⅱ)定义域和有意义
例12 已知函数 .
(1) 若此函数在(-∞,1]上有意义,求a的取值范围.
(2) 若此函数的定义域为(-∞,1] ,求a的取值范围. D解函数问题的几个误区 Ⅲ)值域和取值范围
例13 已知函数f(x)=3x2-(2m+6)x+m+3.
(1)若f(x)≥0恒成立,求m的取值范围.
(2) 若f(x)的值域为 ,求m的取值范围. D解函数问题的几个误区 Ⅳ)自身对称和互相对称
例14 设 f (x)定义在实数集R上.
(1)若f (1+x)= f (1-x) ,求f (x)图象的对称轴.
(2)若y=f(1+x)与y=f(1-x)的图像关于直线l 对称,
求直线l 的方程. D解函数问题的几个误区 V)恒成立,能成立,恰成立
例15 求实数a的范围:
(1) x2-ax-a>0恒成立.
(2) 存在x,使-x2+ax+a>0成立.
(3) 设a>1,不等式 的
解集为(1,+∞). . 2 数形结合思想---图形帮助解题 数与形是事物的两个方面,正是基于对数与形的抽象研究才产生了数学这门学科,才能使人们能够从不同侧面认识事物,数形结合思想就是要使抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维结合起来,华罗庚先生说过:“数与形本是两依倚,焉能分作两边飞. 数缺形时少直观, 形少数时难入微.”.数形结合思想是一种重要的解题思想,用这种思想指导,一些几何问题可以用代数方法来处理,例如解析几何,一些代数问题又可以用几何图形帮助解决,下面主要讲如何用图形帮助解题,这也是高考命题中主要考查的一个内容. 2 数形结合思想---图形帮助解题 A 利用图形求解的个数
例1 圆x2+2x+y2+4y-3=0到直线x+y+1=0的距离等于
的点共有( ).
(A)1个 (B)2个 (C)3个(D)4个
(1991年,全国高考) 用图形分析法求解的个数,实际上是转化为求图象交点的个数. 2 数形结合思想---图形帮助解题 求最值问题实际上是探讨图形的极端位置. B 利用图形求最值
例2 如果实数x,y满足等式(x-2)2+y2=3,那么 的最大值
是( ).
(A) (B) (C) (D)
(1990年,全国高考 ) 2 数形结合思想---图形帮助解题 C 利用图形求参数的范围 例3 橢圆 的焦点为F1 ,F2 ,点P为其上的动点,
当∠F1PF2为钝角时, 点P的横坐标的取值范围是___
(2002年,新课程卷) . 2 数形结合思想---图形帮助解题 C 利用图形求参数的范围 例4 已知两条直线l1:y=x,l2:ax-y=0,其中a为实数,当这两条
直线的夹角在 内变动时,a的变化范围是( ).
(0,1) (B)( (C )( (D)
(2000年,新课程卷) 2 数形结合思想---图形帮助解题 C 利用图形求参数的范围 求参数的范围实质上是弄清参数的几何意义,然后讨论参数所代表的几何意义的变化状态. 例5 设函数f (x ) = 若f (x0 )>1,则x0
的取值范围是( )。
(A) (-1,1) (B) (-1,+∞)
(C) (-∞,-2)∪(1,+∞) (D) (-∞,-1)∪(1,+∞)
(2003年,新课程卷) 2 数形结合思想---图形帮助解题 D 利用图形解不等式 例6 设函数 ,其中a>0,
⑴ 解不等式f(x)≤1;
⑵求a的取值范围,使f(x)在(0,+∞)上单调.
(2000年,全国高考) 2 数形结合思想---图形帮助解题 D 利用图形解不等式 用图形解不等式实际上是研究图象中符合条件的变量的变化范围. 例7 已知 i , m , n 是正整数,且1<i≤m<n.
(II) 证明 (1+m)n>(1+n)m .
(2001年,全国高考) 2 数形结合思想---图形帮助解题 E 利用图形求值 例8 求
的值.
(1992年,全国高考) 2 数形结合思想---图形帮助解题 E 利用图形求值 用图形分析法求值实际上是构造几何图形解题 . 例9???过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是( ).
(A) (B)
(C) (D)
(2000年, 新课程卷) 3分类讨论思想---分情况解决问题 例1? 设a为常数,函数f(x) =x2+|x-a|+1, x ∈ R.
(I) 讨论f(x)的奇偶性;
(II)求f(x)的最小值.
(2002年,全国高考)
3分类讨论思想---分情况解决问题 例2? 设a>0,求函数
的单调区间。
(2003年,新课程卷,理工)
3分类讨论思想---分情况解决问题 例3 某城市在中心广场建造一个花圃,花圃分为6个部分
(如图),现要栽种4种不同颜色的花,每部分栽种一种且相
邻部分不能栽种同样的颜色的花,不同的栽种方法有_____
种(以数字作答). (2003年,新课程卷)
3分类讨论思想---分情况解决问题 4 化归思想---化生题为熟题 4 化归思想---化生题为熟题 4 化归思想---化生题为熟题例2、如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90o,侧棱AA1=2 ,D,E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ ABD的重心G.
(Ⅰ)求A1B与平面ABD所成角的大小;
(结果用反三角函数表示)
(Ⅱ)求点A1到平面AED的距离。
(2003年新课程卷,全国卷) 4 化归思想---化生题为熟题例3 设对所有实数x,不等式
恒成立,求a的取值范围. Thank you
同课章节目录
