数学高考与理性思维[下学期]
图片预览









文档简介
课件48张PPT。一.2003年数学高考与理性思维能力 高考数学试题提出 “以能力立意命题”,正是为了更好地考查数学思想,促进考生理性思维的发展。
数学思维能力是数学能力的核心,而理性思维是一种有明确思维方向,有充分思维依据,有数学思想指导和介入的思维。
理性思维能力包括:逻辑推理,演绎证明,归纳抽象,直觉猜想,运算求解等方面的内容。(一). 逻辑推理和演绎证明能力 第一层次:会观察,比较,分析,综合,
抽象和概括;
第二层次:会用归纳,演绎,和类比进行
推理;
第三层次:会用简明, 准确的数学语言
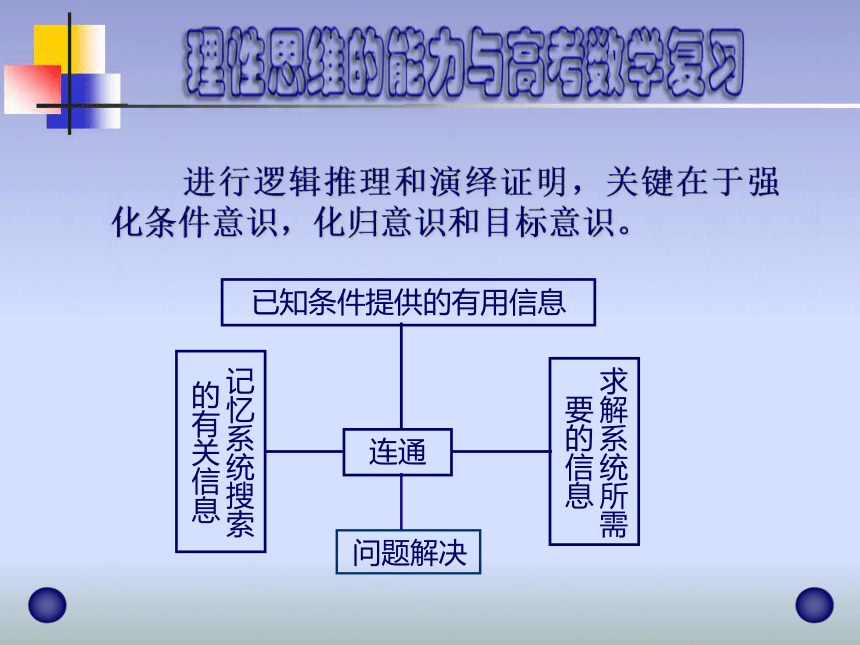
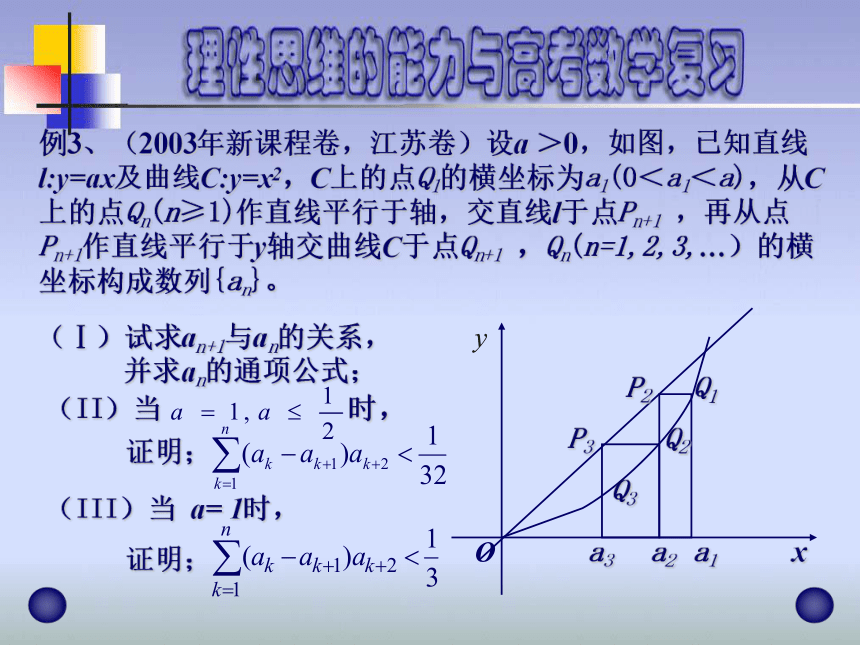
阐述自己的思想和观点。 进行逻辑推理和演绎证明,关键在于强化条件意识,化归意识和目标意识。 问题解决例1、(2003年新课程卷,理工类)设 ,
求函数
的单调区间。 例4.已知 是实数,函数
当 时,
证明:当 时,
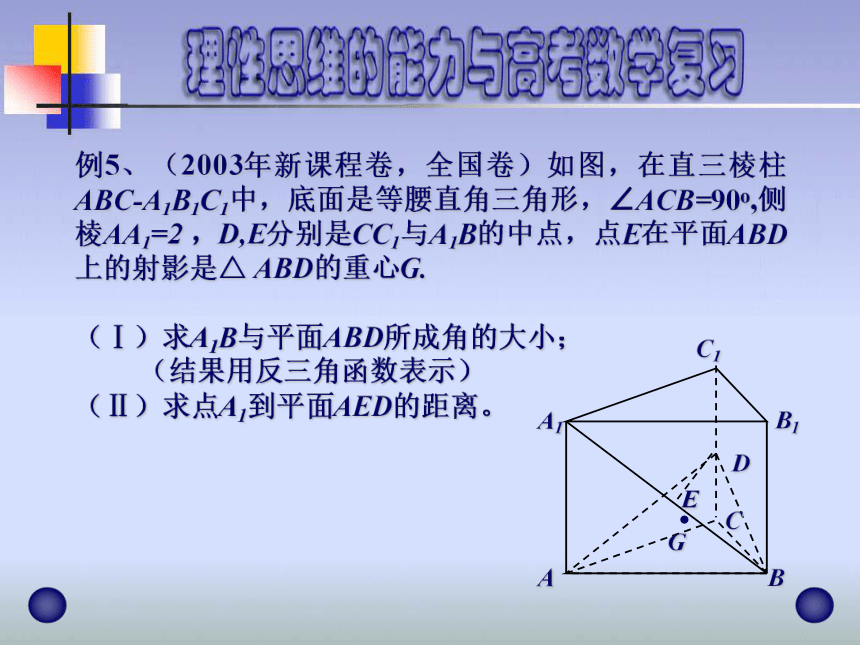
例5、(2003年新课程卷,全国卷)如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90o,侧棱AA1=2 ,D,E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ ABD的重心G.
(Ⅰ)求A1B与平面ABD所成角的大小;
(结果用反三角函数表示)
(Ⅱ)求点A1到平面AED的距离。
●提高逻辑推理和演绎证明能力,关键在于加强条件意识、目标意识和化归意识。
●要注意根据已知条件系统和目标求解系统的信息,从记忆系统搜索有用的信息进行化归。
●思维方向明确,思维依据充分,思维指导正确,就有利于进行逻辑推理和演绎证明。
(二) 归纳抽象能力例1、(2003年新课程卷,全国卷,文史类)在平面几何里,有勾股定理:“设△ABC的两边AB, AC互相垂直,则AB2+AC2=BC2拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC,ACD,ADB两两互相垂直,则______________”。
例2、(2003年上海卷,理工类)已知数列{an}
(n为正整数)是首项为a1 ,公比为q的等比数列。
(Ⅰ)求和: , ;
(Ⅱ)由(Ⅰ)的结果归纳概括出关于正整数的一个结论,并加以证明。
例3、(2003年新课程卷)某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样的颜色的花,不同的栽种方法有__________种(以数字作答)。
例4、(2003年全国卷)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一种颜色,现有4种颜色可供选择,则不同的着色方法共有__________种(以数字作答)。
例5、(2003年新课程卷)设a0为常数,且
an=3n-1-2an-1 ,(n∈N+)
(Ⅰ)证明对任意n≥ 1, ;
(Ⅱ)假设对任意n≥1,有an>an-1 ,求a0的取值范围。
●归纳抽象能力主要体现为归纳能力,类比联想能力和探究能力。
●发现属性,发现关系,发现相似性,注意总结一般规律,是提高归纳抽象能力的关键。(三) 直觉猜想能力例1、(2003年新课程,全国卷,文史类)不等
式 的解集是( )。
(A) (0,2) (B) (2,+∞)
(C) (2,4] (D) (-∞,0)∪(2,+∞)
例2、(2003年新课程)函数 ,
的反函数为( )。
(A) (B)
(C) (D)
例3(2003年新课程,全国卷)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1) ,一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1 ,依次反射到CD,DA和AB上的点P2 ,P3和P4(入射角等于反射角),设P4的坐标为(x4,0),若1<x4<2,则tanθ的取值范围是( )。
(A) (B) (C) (D)
例4(2003年上海卷,理工类)设
均为非零实数,不等式 和
的解集分别为集合M和N,那么 是“M=N”的( )。
(A) 充分非必要条件 (B) 必要非充分条件
(C) 充要条件 (D) 既非充分又非必要条件
例5(2003年新课程卷)一个四面体的所有棱长都是 ,四个顶点在同一球面上,则此球的表面积为( ).
(A) (B) (C) (D)
例6.(1998年,全国卷)一个直角三角形三内角的正弦值成等比数列,其最小内角为( ).
例7(2000年.全国卷)已知两直线
其中 为实数,当这两条直线的夹角在 内变动时, 的取值范围是( ). 例8.在正n棱锥中,相邻两侧面所成的
二面角的取值范围是( ).
●用直觉猜想解题关键在于充分利用题目给出的信息,抓住题目的本质,从而缩短思维链.
●对选择题估算可采取特殊化策略、整体化策略、局部化策略、极限化策略和图形化策略.(四) 运算求解能力 第一层次:会根据法则、公式,定理,定律
正确地运算.
第二层次:理解算理,能够根据题目的 条
件寻求合理、简捷的运算途径,以 达到准确,
熟练、迅速的运算目的. 例1.(2003年新课程卷)已知常数 a>0 ,向量 c=(0,a), i=(1,0),经过原点O以c+ i为方向向量的直线与经过定点 A(0,a)以i-2 c为方向量的直线相交于点P,其中 ∈R,试问:是否存在两个定点E,F,使得|PE|+|PF|为定值,若存在,求出E,F的坐标,若不存在,说明理由。
λλλ 例2.(2003年,全国卷) P: 函数 y= cx 在R上
单调递减,Q: x+|x-2c| > 1 不等式的解集为
R, 如果P和Q有且仅有一个正确,求c的取
值范围.例3、(2003年新课程卷,文史类)已知函数
是R上的偶函数,其图像关于点
对称,且在区间 上是单调函数,求
和ω的值。 例4.(2003年上海卷)已知集合M是满足下列性质的函数的全体:存在非零常数T,对任意x∈R,有f(x+T )= T f(x)成立。
(1)函数f(x)=x是否属于集合M ?说明理由;
(2)设函数f(x)=ax(a>0,且a≠1)的图像与y=x的图像有公共点,证明: f(x)=ax ∈ M ;
(3)若函数f(x)=sinkx∈M ,求实数k的取值范围。 ●对运算求解能力,掌握算理,根据条
件寻求合理、简捷的运算途径是关键。
●运算的准确性、熟练性、合理性、简
捷性是运算能力的基本要求。
二、如何有效地进行高考复习 第一.高考数学复习的目的和任务是什么?
第二.高考数学复习的功能和作用是什么?
第三.高考复习的基本原则是什么?
(一)高考数学复习的目的和任务 1.查漏补缺,梳理知识,形成完整的知识网络,
整体把握数学认知结构;
2.进一步巩固和掌握三基(基本知识,基本技
能和基本思想方法);
3.总结规律,加深理解,促进理性思维能力的
发展;
4.强化思维训练,提高解题能力和探索创新能
力,发展数学智慧。 (二)高考复习的功能1.巩固功能——通过复习全面回忆所学的基本知识、基本技能和基本数学思想,形成记忆,作为知识和技能的准备;
2.提高功能——通过复习从整体上把握知识内在联系和规律,深化对知识的理解和认识,提高对数学的认识水平和解题水平;3.转化功能——通过复习,转化为数学能力,包括逻辑思维能力,空间想象能力,运算求解能力,分析问题和解决问题的能力和创新探索能力。
——通过对知识的深化理解,掌握以知识为主体、主线建立知识网络的
思维方法;
——通过对知识网络的理解,提高知识综合运用的能力和数学联结能力;
——通过对数学思维规律的认识,提高归纳总结解题规律和方法的能力,
培养思维品质;
——通过问题解决的复习,提高理性思维能力和创新探索能力。
4.发展功能——通过复习达到从量的积累到质的飞跃,通过对数学知识的复习与组织,通过对各知识点的逻辑关系的把握、交汇与联结,促进智能迁移。
——能够按一定思路,综合运用知识解决问题;
——能够用数学思想方法指导解题;
——能够有效地进行模式识别;
——能够评价不同解题方法的优劣。(三)高考复习的若干原则1.基础、系统原则 乌申斯基指出:“智力就是形成系统的知识”,系统化、结构化、网络化的知识便于记忆、理解、检索和运用。
(2003年新课程卷)O是平面上一定点,A,B,C是平面
上不共线的三个点,动点P满足 ,
,则P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
2.精选、综合原则 量不在多,典型就行,
题不在难,有思想就灵。
3.思想能力训练贯彻始终原则4.稳扎稳打原则 ——稳在审题上
——稳在思维过程上
——稳在解题后的反思上
——稳在认真计算和规范表达上 1.对审题的反思;
2.对解题思维过程的反思;
3.对解法多样化的反思;
4.对题目本身及解法本身所存在的规律
的反思;
5.对题目变化的反思。
Thank you!
数学思维能力是数学能力的核心,而理性思维是一种有明确思维方向,有充分思维依据,有数学思想指导和介入的思维。
理性思维能力包括:逻辑推理,演绎证明,归纳抽象,直觉猜想,运算求解等方面的内容。(一). 逻辑推理和演绎证明能力 第一层次:会观察,比较,分析,综合,
抽象和概括;
第二层次:会用归纳,演绎,和类比进行
推理;
第三层次:会用简明, 准确的数学语言
阐述自己的思想和观点。 进行逻辑推理和演绎证明,关键在于强化条件意识,化归意识和目标意识。 问题解决例1、(2003年新课程卷,理工类)设 ,
求函数
的单调区间。 例4.已知 是实数,函数
当 时,
证明:当 时,
例5、(2003年新课程卷,全国卷)如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90o,侧棱AA1=2 ,D,E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ ABD的重心G.
(Ⅰ)求A1B与平面ABD所成角的大小;
(结果用反三角函数表示)
(Ⅱ)求点A1到平面AED的距离。
●提高逻辑推理和演绎证明能力,关键在于加强条件意识、目标意识和化归意识。
●要注意根据已知条件系统和目标求解系统的信息,从记忆系统搜索有用的信息进行化归。
●思维方向明确,思维依据充分,思维指导正确,就有利于进行逻辑推理和演绎证明。
(二) 归纳抽象能力例1、(2003年新课程卷,全国卷,文史类)在平面几何里,有勾股定理:“设△ABC的两边AB, AC互相垂直,则AB2+AC2=BC2拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC,ACD,ADB两两互相垂直,则______________”。
例2、(2003年上海卷,理工类)已知数列{an}
(n为正整数)是首项为a1 ,公比为q的等比数列。
(Ⅰ)求和: , ;
(Ⅱ)由(Ⅰ)的结果归纳概括出关于正整数的一个结论,并加以证明。
例3、(2003年新课程卷)某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样的颜色的花,不同的栽种方法有__________种(以数字作答)。
例4、(2003年全国卷)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一种颜色,现有4种颜色可供选择,则不同的着色方法共有__________种(以数字作答)。
例5、(2003年新课程卷)设a0为常数,且
an=3n-1-2an-1 ,(n∈N+)
(Ⅰ)证明对任意n≥ 1, ;
(Ⅱ)假设对任意n≥1,有an>an-1 ,求a0的取值范围。
●归纳抽象能力主要体现为归纳能力,类比联想能力和探究能力。
●发现属性,发现关系,发现相似性,注意总结一般规律,是提高归纳抽象能力的关键。(三) 直觉猜想能力例1、(2003年新课程,全国卷,文史类)不等
式 的解集是( )。
(A) (0,2) (B) (2,+∞)
(C) (2,4] (D) (-∞,0)∪(2,+∞)
例2、(2003年新课程)函数 ,
的反函数为( )。
(A) (B)
(C) (D)
例3(2003年新课程,全国卷)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1) ,一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1 ,依次反射到CD,DA和AB上的点P2 ,P3和P4(入射角等于反射角),设P4的坐标为(x4,0),若1<x4<2,则tanθ的取值范围是( )。
(A) (B) (C) (D)
例4(2003年上海卷,理工类)设
均为非零实数,不等式 和
的解集分别为集合M和N,那么 是“M=N”的( )。
(A) 充分非必要条件 (B) 必要非充分条件
(C) 充要条件 (D) 既非充分又非必要条件
例5(2003年新课程卷)一个四面体的所有棱长都是 ,四个顶点在同一球面上,则此球的表面积为( ).
(A) (B) (C) (D)
例6.(1998年,全国卷)一个直角三角形三内角的正弦值成等比数列,其最小内角为( ).
例7(2000年.全国卷)已知两直线
其中 为实数,当这两条直线的夹角在 内变动时, 的取值范围是( ). 例8.在正n棱锥中,相邻两侧面所成的
二面角的取值范围是( ).
●用直觉猜想解题关键在于充分利用题目给出的信息,抓住题目的本质,从而缩短思维链.
●对选择题估算可采取特殊化策略、整体化策略、局部化策略、极限化策略和图形化策略.(四) 运算求解能力 第一层次:会根据法则、公式,定理,定律
正确地运算.
第二层次:理解算理,能够根据题目的 条
件寻求合理、简捷的运算途径,以 达到准确,
熟练、迅速的运算目的. 例1.(2003年新课程卷)已知常数 a>0 ,向量 c=(0,a), i=(1,0),经过原点O以c+ i为方向向量的直线与经过定点 A(0,a)以i-2 c为方向量的直线相交于点P,其中 ∈R,试问:是否存在两个定点E,F,使得|PE|+|PF|为定值,若存在,求出E,F的坐标,若不存在,说明理由。
λλλ 例2.(2003年,全国卷) P: 函数 y= cx 在R上
单调递减,Q: x+|x-2c| > 1 不等式的解集为
R, 如果P和Q有且仅有一个正确,求c的取
值范围.例3、(2003年新课程卷,文史类)已知函数
是R上的偶函数,其图像关于点
对称,且在区间 上是单调函数,求
和ω的值。 例4.(2003年上海卷)已知集合M是满足下列性质的函数的全体:存在非零常数T,对任意x∈R,有f(x+T )= T f(x)成立。
(1)函数f(x)=x是否属于集合M ?说明理由;
(2)设函数f(x)=ax(a>0,且a≠1)的图像与y=x的图像有公共点,证明: f(x)=ax ∈ M ;
(3)若函数f(x)=sinkx∈M ,求实数k的取值范围。 ●对运算求解能力,掌握算理,根据条
件寻求合理、简捷的运算途径是关键。
●运算的准确性、熟练性、合理性、简
捷性是运算能力的基本要求。
二、如何有效地进行高考复习 第一.高考数学复习的目的和任务是什么?
第二.高考数学复习的功能和作用是什么?
第三.高考复习的基本原则是什么?
(一)高考数学复习的目的和任务 1.查漏补缺,梳理知识,形成完整的知识网络,
整体把握数学认知结构;
2.进一步巩固和掌握三基(基本知识,基本技
能和基本思想方法);
3.总结规律,加深理解,促进理性思维能力的
发展;
4.强化思维训练,提高解题能力和探索创新能
力,发展数学智慧。 (二)高考复习的功能1.巩固功能——通过复习全面回忆所学的基本知识、基本技能和基本数学思想,形成记忆,作为知识和技能的准备;
2.提高功能——通过复习从整体上把握知识内在联系和规律,深化对知识的理解和认识,提高对数学的认识水平和解题水平;3.转化功能——通过复习,转化为数学能力,包括逻辑思维能力,空间想象能力,运算求解能力,分析问题和解决问题的能力和创新探索能力。
——通过对知识的深化理解,掌握以知识为主体、主线建立知识网络的
思维方法;
——通过对知识网络的理解,提高知识综合运用的能力和数学联结能力;
——通过对数学思维规律的认识,提高归纳总结解题规律和方法的能力,
培养思维品质;
——通过问题解决的复习,提高理性思维能力和创新探索能力。
4.发展功能——通过复习达到从量的积累到质的飞跃,通过对数学知识的复习与组织,通过对各知识点的逻辑关系的把握、交汇与联结,促进智能迁移。
——能够按一定思路,综合运用知识解决问题;
——能够用数学思想方法指导解题;
——能够有效地进行模式识别;
——能够评价不同解题方法的优劣。(三)高考复习的若干原则1.基础、系统原则 乌申斯基指出:“智力就是形成系统的知识”,系统化、结构化、网络化的知识便于记忆、理解、检索和运用。
(2003年新课程卷)O是平面上一定点,A,B,C是平面
上不共线的三个点,动点P满足 ,
,则P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
2.精选、综合原则 量不在多,典型就行,
题不在难,有思想就灵。
3.思想能力训练贯彻始终原则4.稳扎稳打原则 ——稳在审题上
——稳在思维过程上
——稳在解题后的反思上
——稳在认真计算和规范表达上 1.对审题的反思;
2.对解题思维过程的反思;
3.对解法多样化的反思;
4.对题目本身及解法本身所存在的规律
的反思;
5.对题目变化的反思。
Thank you!
同课章节目录
