9.2.1总体取值规律的估计 课时作业(含答案)
文档属性
| 名称 | 9.2.1总体取值规律的估计 课时作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 750.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 00:00:00 | ||
图片预览


文档简介
9.2.1总体取值规律的估计 课时作业
一、单选题
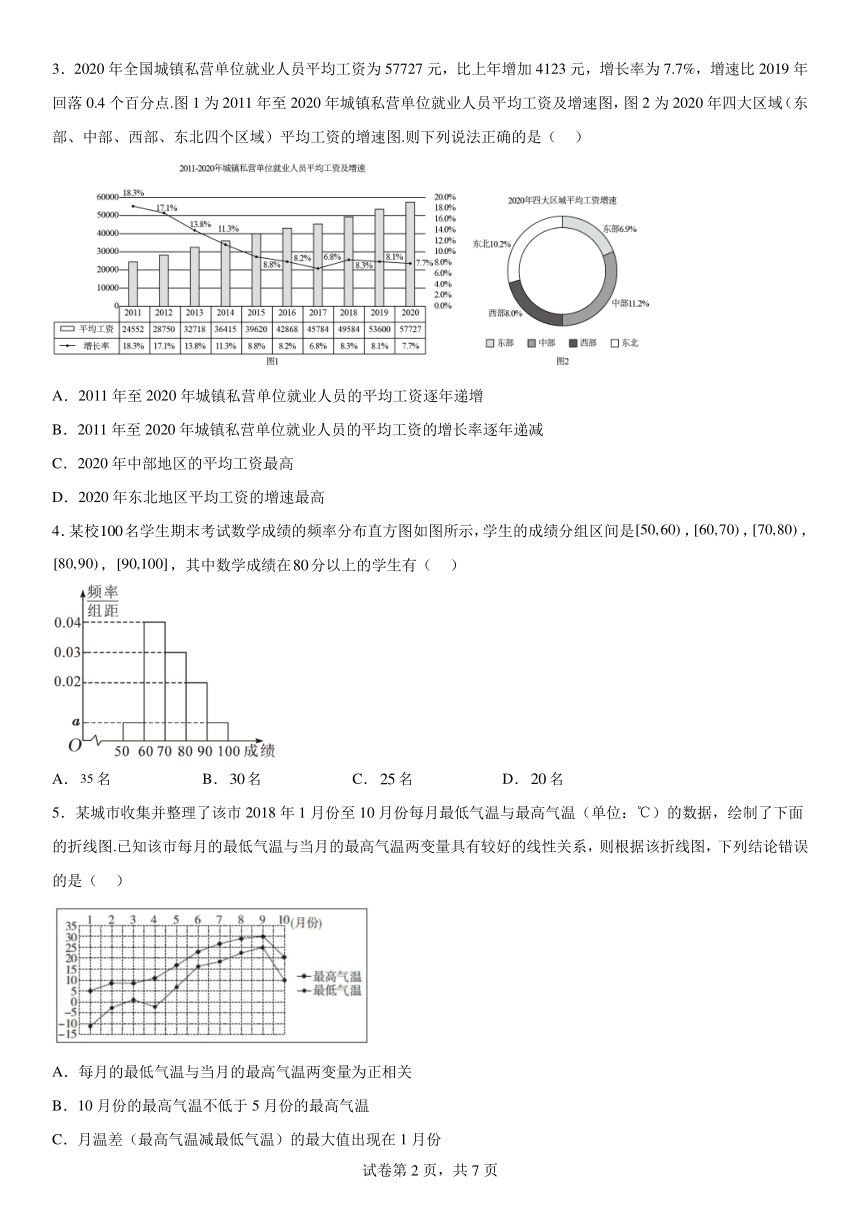
1.某次病毒疫情爆发后,为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应.如图表示1月21日至3月7日病毒单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.累计确诊人数在2月12日左右达到峰值
D.2月10日至2月14日新增确诊人数波动最大
2.如图是某年第一季度五个省GDP的情况图,则下列陈述正确的是
①该年第一季度GDP总量和增长率均居同一位的省只有1个;
②与去年周期相比,该年第一季度五个省的GDP总量均实现了增长;
③去年同期的GDP总量位于前三位的是山东、江苏、浙江;
④去年同期浙江的GDP总量也是第三位.
A.①② B.②③④ C.②④ D.①③④
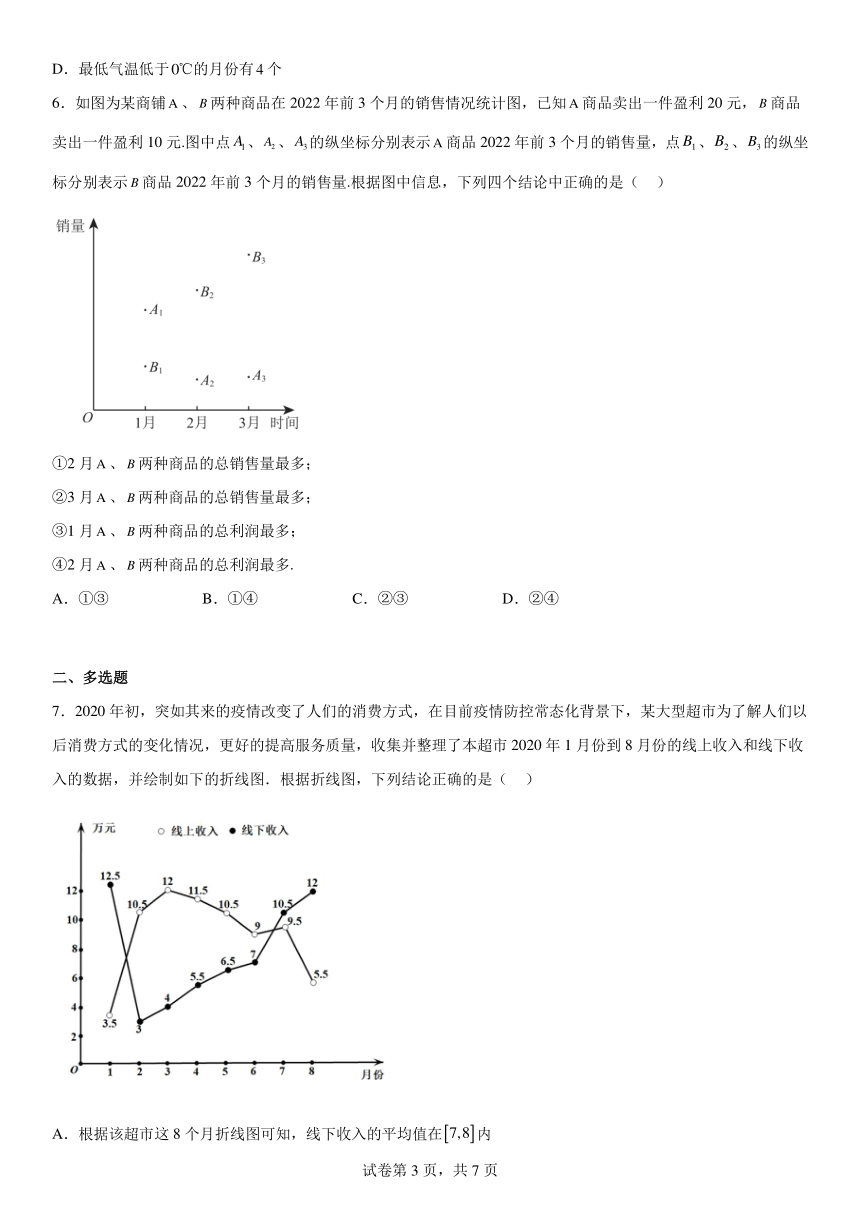
3.2020年全国城镇私营单位就业人员平均工资为57727元,比上年增加4123元,增长率为7.7%,增速比2019年回落0.4个百分点.图1为2011年至2020年城镇私营单位就业人员平均工资及增速图,图2为2020年四大区域(东部、中部、西部、东北四个区域)平均工资的增速图.则下列说法正确的是( )
A.2011年至2020年城镇私营单位就业人员的平均工资逐年递增
B.2011年至2020年城镇私营单位就业人员的平均工资的增长率逐年递减
C.2020年中部地区的平均工资最高
D.2020年东北地区平均工资的增速最高
4.某校名学生期末考试数学成绩的频率分布直方图如图所示,学生的成绩分组区间是,,,,,其中数学成绩在分以上的学生有( )
A.名 B.名 C.名 D.名
5.某城市收集并整理了该市2018年1月份至10月份每月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A.每月的最低气温与当月的最高气温两变量为正相关
B.10月份的最高气温不低于5月份的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月份
D.最低气温低于的月份有个
6.如图为某商铺、两种商品在2022年前3个月的销售情况统计图,已知商品卖出一件盈利20元,商品卖出一件盈利10元.图中点、、的纵坐标分别表示商品2022年前3个月的销售量,点、、的纵坐标分别表示商品2022年前3个月的销售量.根据图中信息,下列四个结论中正确的是( )
①2月、两种商品的总销售量最多;
②3月、两种商品的总销售量最多;
③1月、两种商品的总利润最多;
④2月、两种商品的总利润最多.
A.①③ B.①④ C.②③ D.②④
二、多选题
7.2020年初,突如其来的疫情改变了人们的消费方式,在目前疫情防控常态化背景下,某大型超市为了解人们以后消费方式的变化情况,更好的提高服务质量,收集并整理了本超市2020年1月份到8月份的线上收入和线下收入的数据,并绘制如下的折线图.根据折线图,下列结论正确的是( )
A.根据该超市这8个月折线图可知,线下收入的平均值在内
B.根据该超市这8个月折线图可知,线上收入的极差比线下收入的极差大
C.根据该超市这8个月折线图可知,每月总收入与时间呈现负相关
D.根据该超市这8个月折线图可知,在疫情逐步得到有效控制后,人们比较愿意线下消费
8.某中学四位同学利用假期到一贫困村参加社会实践活动,感受年该村精准扶贫及新农村建设的变化.经过实地调查显示,该村年的经济收入增加了一倍.实现翻番,精准扶贫取得惊人成果.为更好地了解该村的经济收入变化情况,为后期精准扶贫方向提供决策参考,四位同学统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
四位同学依据上述饼图,分别得出以下四个结论,其中结论中正确的是( )
A.精准扶贫及新农村建设后,种植收入减少
B.精准扶贫及新农村建设后,其他收入增加了一倍以上
C.精准扶贫及新农村建设后,养殖收入增加了一倍
D.精准扶贫及新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
三、填空题
9.某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成5组:,,,,,得到如图所示的频率直方图,如果从左到右的5个小矩形的面积之比为,那么成绩小于16秒的学生共有______人.
10.如图是一次数学考试成绩的样本频率分布直方图(样本容量),若成绩在60分到80分之间的学生称为“临界生”,那么样本中“临界生”人数约为___________.
11.在某个容量为100的样本的频率分布直方图中,共有5小长方形,若中间一个小长方形的面积等于其他4个小长方形面积和的,则中间一组的频数为_______.
12.昆明市市花为云南山茶花,又名滇山茶,原产云南,国家二级保护植物,为了监测滇山茶的生长情况,从不同林区随机抽取100株测量胸径(厘米)作为样本,得到样本频率分布直方图如图所示,则纵坐标___________.
四、解答题
13.小明同学因发热而住院,下图是根据护士为他测量的体温所绘制的体温折线图.
根据图中的信息,回答以下问题:
(1)护士每隔几小时给小明测量一次体温?
(2)近三天来,小明的最高体温、最低体温分别是多少?
(3)从体温看,小明的病情是在恶化还是在好转?
(4)如果连续36小时体温不超过37.2摄氏度的话,可认为基本康复,那么小明最快什么出院?
14.2019年某饮料公司计划从,两款新配方饮料中选择一款进行新品推介,现对这两款饮料进行市场调查,让接受调查的受访者同时饮用这两种饮料,并分别对两款饮料进行评分,现对接受调查的100万名受访者的评分进行整理得到如下统计图.
从对以往调查数据分析可以得出如下结论:评分在的受访者中有20%会购买,评分在的受访者中有60%会购买,评分在的受访者中有90%会购买.
(1)在受访的100万人中,估计至少对一款饮料评分在60分以下的受访者人数的最大值与最小值(单位:万人);
(2)如果你是决策者,新品推介你会主推哪一款饮料,并说明你的理由.
15.某小学为了了解三年级学生的身高情况,用随机抽样的方法获得了校内20名三年级学生的身高(单位:厘米),结果如下:
104 111 112 115 117
117 118 119 121 123
126 128 129 129 133
135 136 138 142 145
试估计该小学三年级学生身高大于等于110厘米且小于120厘米的学生的占比.
16.2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
(Ⅰ)求的值,并作出这些数据的频率分布直方图;
(Ⅱ)假设每组数据组间是平均分布的,试估计该组数据的平均数;(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”,经过比赛后从这6人中选拔2人组成该校代表队,求这2人来自不同组别的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.A
4.C
5.D
6.C
7.AD
8.BCD
9.66
10.30
11.20
12.
13.(1)每隔6小时给小明测量一次体温;
(2)最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(3)病情在好转;
(4)最快可以在9月10凌晨6时出院.
14.(1)最大值为30万人,最小值为20万人;(2)新品推介应该主推款饮料,理由见解析.
15.35%.
16.(Ⅰ)详见解析;(Ⅱ)12.25;(Ⅲ).
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某次病毒疫情爆发后,为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应.如图表示1月21日至3月7日病毒单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.累计确诊人数在2月12日左右达到峰值
D.2月10日至2月14日新增确诊人数波动最大
2.如图是某年第一季度五个省GDP的情况图,则下列陈述正确的是
①该年第一季度GDP总量和增长率均居同一位的省只有1个;
②与去年周期相比,该年第一季度五个省的GDP总量均实现了增长;
③去年同期的GDP总量位于前三位的是山东、江苏、浙江;
④去年同期浙江的GDP总量也是第三位.
A.①② B.②③④ C.②④ D.①③④
3.2020年全国城镇私营单位就业人员平均工资为57727元,比上年增加4123元,增长率为7.7%,增速比2019年回落0.4个百分点.图1为2011年至2020年城镇私营单位就业人员平均工资及增速图,图2为2020年四大区域(东部、中部、西部、东北四个区域)平均工资的增速图.则下列说法正确的是( )
A.2011年至2020年城镇私营单位就业人员的平均工资逐年递增
B.2011年至2020年城镇私营单位就业人员的平均工资的增长率逐年递减
C.2020年中部地区的平均工资最高
D.2020年东北地区平均工资的增速最高
4.某校名学生期末考试数学成绩的频率分布直方图如图所示,学生的成绩分组区间是,,,,,其中数学成绩在分以上的学生有( )
A.名 B.名 C.名 D.名
5.某城市收集并整理了该市2018年1月份至10月份每月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A.每月的最低气温与当月的最高气温两变量为正相关
B.10月份的最高气温不低于5月份的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月份
D.最低气温低于的月份有个
6.如图为某商铺、两种商品在2022年前3个月的销售情况统计图,已知商品卖出一件盈利20元,商品卖出一件盈利10元.图中点、、的纵坐标分别表示商品2022年前3个月的销售量,点、、的纵坐标分别表示商品2022年前3个月的销售量.根据图中信息,下列四个结论中正确的是( )
①2月、两种商品的总销售量最多;
②3月、两种商品的总销售量最多;
③1月、两种商品的总利润最多;
④2月、两种商品的总利润最多.
A.①③ B.①④ C.②③ D.②④
二、多选题
7.2020年初,突如其来的疫情改变了人们的消费方式,在目前疫情防控常态化背景下,某大型超市为了解人们以后消费方式的变化情况,更好的提高服务质量,收集并整理了本超市2020年1月份到8月份的线上收入和线下收入的数据,并绘制如下的折线图.根据折线图,下列结论正确的是( )
A.根据该超市这8个月折线图可知,线下收入的平均值在内
B.根据该超市这8个月折线图可知,线上收入的极差比线下收入的极差大
C.根据该超市这8个月折线图可知,每月总收入与时间呈现负相关
D.根据该超市这8个月折线图可知,在疫情逐步得到有效控制后,人们比较愿意线下消费
8.某中学四位同学利用假期到一贫困村参加社会实践活动,感受年该村精准扶贫及新农村建设的变化.经过实地调查显示,该村年的经济收入增加了一倍.实现翻番,精准扶贫取得惊人成果.为更好地了解该村的经济收入变化情况,为后期精准扶贫方向提供决策参考,四位同学统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
四位同学依据上述饼图,分别得出以下四个结论,其中结论中正确的是( )
A.精准扶贫及新农村建设后,种植收入减少
B.精准扶贫及新农村建设后,其他收入增加了一倍以上
C.精准扶贫及新农村建设后,养殖收入增加了一倍
D.精准扶贫及新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
三、填空题
9.某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成5组:,,,,,得到如图所示的频率直方图,如果从左到右的5个小矩形的面积之比为,那么成绩小于16秒的学生共有______人.
10.如图是一次数学考试成绩的样本频率分布直方图(样本容量),若成绩在60分到80分之间的学生称为“临界生”,那么样本中“临界生”人数约为___________.
11.在某个容量为100的样本的频率分布直方图中,共有5小长方形,若中间一个小长方形的面积等于其他4个小长方形面积和的,则中间一组的频数为_______.
12.昆明市市花为云南山茶花,又名滇山茶,原产云南,国家二级保护植物,为了监测滇山茶的生长情况,从不同林区随机抽取100株测量胸径(厘米)作为样本,得到样本频率分布直方图如图所示,则纵坐标___________.
四、解答题
13.小明同学因发热而住院,下图是根据护士为他测量的体温所绘制的体温折线图.
根据图中的信息,回答以下问题:
(1)护士每隔几小时给小明测量一次体温?
(2)近三天来,小明的最高体温、最低体温分别是多少?
(3)从体温看,小明的病情是在恶化还是在好转?
(4)如果连续36小时体温不超过37.2摄氏度的话,可认为基本康复,那么小明最快什么出院?
14.2019年某饮料公司计划从,两款新配方饮料中选择一款进行新品推介,现对这两款饮料进行市场调查,让接受调查的受访者同时饮用这两种饮料,并分别对两款饮料进行评分,现对接受调查的100万名受访者的评分进行整理得到如下统计图.
从对以往调查数据分析可以得出如下结论:评分在的受访者中有20%会购买,评分在的受访者中有60%会购买,评分在的受访者中有90%会购买.
(1)在受访的100万人中,估计至少对一款饮料评分在60分以下的受访者人数的最大值与最小值(单位:万人);
(2)如果你是决策者,新品推介你会主推哪一款饮料,并说明你的理由.
15.某小学为了了解三年级学生的身高情况,用随机抽样的方法获得了校内20名三年级学生的身高(单位:厘米),结果如下:
104 111 112 115 117
117 118 119 121 123
126 128 129 129 133
135 136 138 142 145
试估计该小学三年级学生身高大于等于110厘米且小于120厘米的学生的占比.
16.2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
(Ⅰ)求的值,并作出这些数据的频率分布直方图;
(Ⅱ)假设每组数据组间是平均分布的,试估计该组数据的平均数;(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”,经过比赛后从这6人中选拔2人组成该校代表队,求这2人来自不同组别的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.A
4.C
5.D
6.C
7.AD
8.BCD
9.66
10.30
11.20
12.
13.(1)每隔6小时给小明测量一次体温;
(2)最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(3)病情在好转;
(4)最快可以在9月10凌晨6时出院.
14.(1)最大值为30万人,最小值为20万人;(2)新品推介应该主推款饮料,理由见解析.
15.35%.
16.(Ⅰ)详见解析;(Ⅱ)12.25;(Ⅲ).
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
