第九章:不等式与不等式组练习题2021-2022学年内蒙古各地七年级下学期人教版数学期末试题选编(含解析)
文档属性
| 名称 | 第九章:不等式与不等式组练习题2021-2022学年内蒙古各地七年级下学期人教版数学期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 473.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 14:55:54 | ||
图片预览




文档简介
第九章:不等式与不等式组 练习题
一、单选题
1.(2022春·内蒙古呼伦贝尔·七年级统考期末)与5的和不大于,用不等式表示为( )
A. B. C. D.
2.(2022春·内蒙古乌兰察布·七年级统考期末)以下所给的数值中,为不等式﹣2x+3<0的解的是( )
A.﹣2 B.﹣1 C. D.2
3.(2022春·内蒙古呼伦贝尔·七年级统考期末)若,则下列不等式中正确的是( )
A. B. C. D.
4.(2022春·内蒙古通辽·七年级统考期末)若关于x的方程x﹣2+3k=的解是正数,则k的取值范围是( )
A.k> B.k≥ C.k< D.k≤
5.(2022春·内蒙古兴安盟·七年级统考期末)已知点P(2a 1,1 a)在第一象限,则a的取值范围在数轴上表示正确的是
A. B. C. D.
6.(2022春·内蒙古呼和浩特·七年级统考期末)已知不等式:①,②,③,④,从这四个不等式中取两个,构成正整数解是2的不等式组是( )
A.①与② B.②与③ C.③与④ D.①与④
7.(2022春·内蒙古通辽·七年级统考期末)若关于的不等式组至多有4个整数解,则的取值范围是( )
A. B. C. D.
8.(2022春·内蒙古兴安盟·七年级统考期末)研究表明,运动时将心率p(次)控制在最佳燃脂心率范围内,能起到燃烧脂肪并且保护心脏功能的作用.最佳燃脂心率最高值不应该超过(220﹣年龄)×0.8,最低值不低于(220﹣年龄)×0.6.以40岁为例计算,220﹣40=180,180×0.8=144,180×0.6=108,所以40岁的年龄最佳燃脂心率的范围用不等式可表示为( )
A.108≤p≤144 B.108<p<144 C.108≤p≤190 D.108<p<190
二、填空题
9.(2022春·内蒙古通辽·七年级统考期末)当_________时,式子的值不大于的值.
10.(2022春·内蒙古巴彦淖尔·七年级统考期末)当x满足_______时,代数式的值是非负数.
11.(2022春·内蒙古巴彦淖尔·七年级统考期末)已知满足不等式的最小整数解是方程的解,则的值为________.
12.(2022春·内蒙古呼和浩特·七年级统考期末)A、B两种花卉的最佳生长温度t分别是度和度,若把这两种花卉放在一起种植,请用不等式表示最佳的生长温度t应控制在范围________.
13.(2022春·内蒙古通辽·七年级统考期末)若不等式组 解集是-1三、解答题
14.(2022春·内蒙古兴安盟·七年级统考期末)【发现问题】已知,求的值.
方法一:先解方程组,得出,的值,再代入,求出的值.
方法二:将①②,求出的值.
【提出问题】怎样才能得到方法二呢?
【分析问题】
为了得到方法二,可以将①②,可得.
令等式左边,比较系数可得,求得.
【解决问题】
(1)请你选择一种方法,求的值;
(2)对于方程组利用方法二的思路,求的值;
【迁移应用】
(3)已知,求的范围.
15.(2022春·内蒙古乌兰察布·七年级统考期末)某学校为了防控新型冠状病毒,购买了甲、乙两种消毒液进行校园环境消毒.已知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元.
(1)每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元
(2)学校准备第三次购买这两种消毒液,其中甲种消毒液比乙种消毒液多10瓶,并且总花费不超过3 500元,最多能购买多少瓶甲种消毒液
16.(2022春·内蒙古鄂尔多斯·七年级统考期末)随着新冠疫情的出现,口罩成为日常生活的必需品,某医药公司每月生产甲、乙两种型号的防疫口罩共20万只,且所有口罩当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/只 4元/只
售价 18元/只 6元/只
(1)若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?
(2)如果该公司四月份投入成本不超过216万元,该医药公司四月份最多只能生产甲种防疫口罩多少万只?
(3)某学校到该公司购买乙型口罩有如下两种方案,方案一:乙型口罩一律打9折;方案二:购买168元会员卡后,乙型口罩一律8折.请帮学校设计出合适的购买方案.
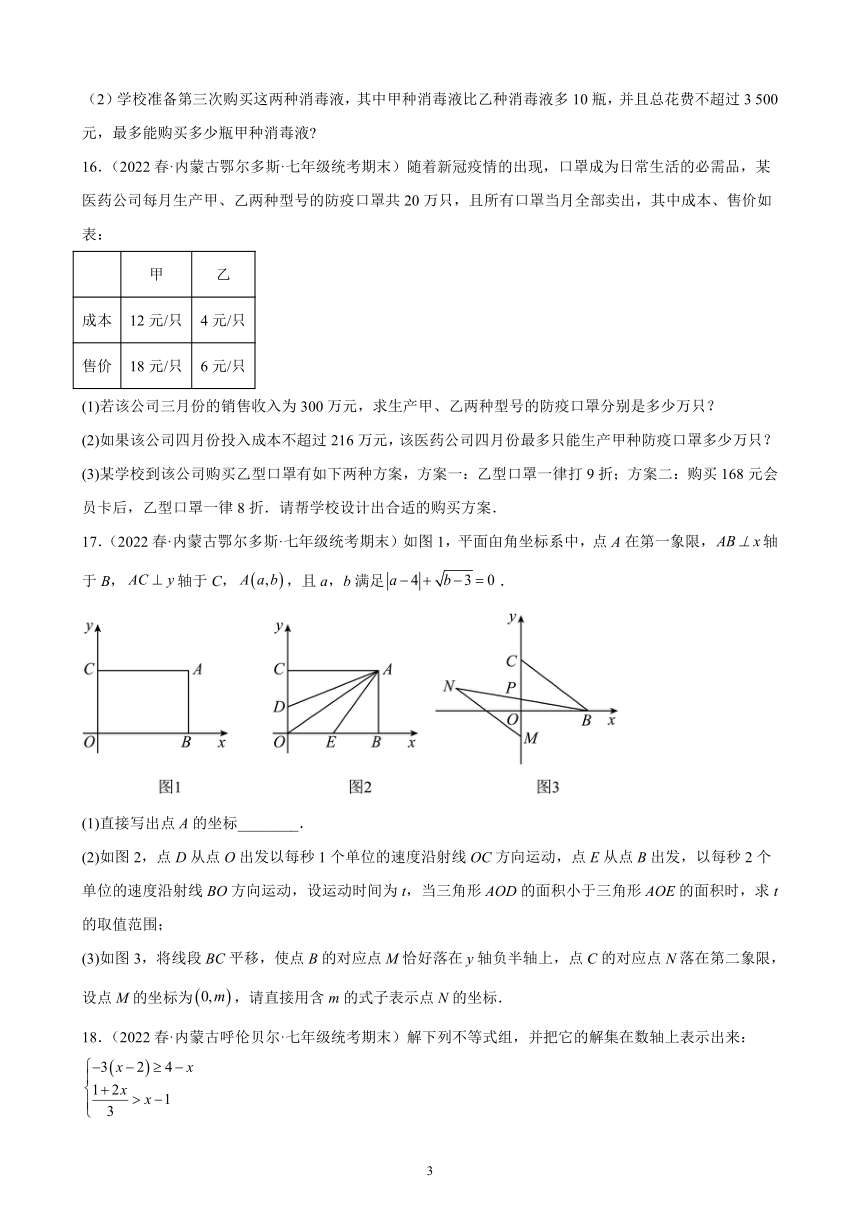
17.(2022春·内蒙古鄂尔多斯·七年级统考期末)如图1,平面甶角坐标系中,点A在第一象限,轴于B,轴于C,,且a,b满足.
(1)直接写出点A的坐标________.
(2)如图2,点D从点O出发以每秒1个单位的速度沿射线OC方向运动,点E从点B出发,以每秒2个单位的速度沿射线BO方向运动,设运动时间为t,当三角形AOD的面积小于三角形AOE的面积时,求t的取值范围;
(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点N落在第二象限,设点M的坐标为,请直接用含m的式子表示点N的坐标.
18.(2022春·内蒙古呼伦贝尔·七年级统考期末)解下列不等式组,并把它的解集在数轴上表示出来:
19.(2022春·内蒙古巴彦淖尔·七年级统考期末)解不等式组,并判断-1、这两个数是不是该不等式组的解.
20.(2022春·内蒙古通辽·七年级统考期末)解不等式组
(1)(把它的解集表示在数轴上).
(2)(并写出它的整数解).
21.(2022春·内蒙古通辽·七年级统考期末)解不等式组并求出不等式组的整数解之和.
22.(2022春·内蒙古通辽·七年级统考期末)某商家欲购进甲、乙两种抗疫用品共180件,其进价和售价如表:
甲 乙
进价(元/件) 14 35
售价(元/件) 20 43
(1)若商家计划销售完这批抗疫用品后能获利1240元,问甲、乙两种用品应分别购进多少件?(请用二元一次方程组求解)
(2)若商家计划投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
23.(2022春·内蒙古呼和浩特·七年级统考期末)快递员把货物送到客户手中称为送件,帮客户寄出货物称为揽件.快递员的提成取决于送件数和揽件数.某快递公司快递员小李若平均每天的送件数和揽件数分别为80件和20件,则他平均每天的提成是160元;若平均每天的送件数和揽件数分别为120件和25件,则他平均每天的提成是230元
(1)求快递员小李平均每送一件和平均每揽一件的提成各是多少元;
(2)已知快递员小李一周内平均每天的送件数和揽件数共计200件,且揽件数不大于送件数的.如果他平均每天的提成不低于318,求他平均每天的送件数.
24.(2022春·内蒙古呼伦贝尔·七年级统考期末)某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 4台 1200元
第二周 5台 6台 1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?若超市销售完这50台电风扇能实现利润超过1850元的目标,请直接给出相应的采购方案.
25.(2022春·内蒙古兴安盟·七年级统考期末)甲、乙两种植户,他们均种植了草莓,葡萄两类水果,两种植户种植的两类水果的种植面积与总收入如下表:
种植户 种植草莓面积(单位:亩) 种植葡萄面积(单位:亩) 总收入(单位:万元)
甲 3 2 14
乙 2 5 18.5
说明:不同种植户种植的同类水果每亩平均收入相等.
(1)求草莓、葡萄两类水果每亩平均收入各是多少万元?
(2)某种植户准备租15亩地用来种植草莓、葡萄两类水果,为了使总收入不低于40万元,且种植草莓的面积不超过种植葡萄的面积(两类水果的种植面积均为整数),求该种植户所有种植方案.
参考答案:
1.D
【分析】读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式,不大于即小于或等于.
【详解】解:“与5的和不大于-1”用不等式表示为,
故选:D.
【点睛】此题考查利用字母来表示题目中的不等关系,抓住大于、小于、不大于、不小于等关键字.
2.D
【详解】解:-2x<-3,x>,
∴不等式的解集是:x>.
故选D.
3.A
【分析】根据不等式的性质逐项判断即得答案.
【详解】解:A、若,则,故本选项变形正确,符合题意;
B、若,则,故本选项变形错误,不符合题意;
C、若,则,故本选项变形错误,不符合题意;
D、若,则,故本选项变形错误,不符合题意.
故选:A.
【点睛】本题考查了不等式的性质,属于基础题型,熟练掌握不等式的性质是解题关键.
4.C
【详解】解方程x﹣2+3k=得:x=-4k+3,
∵方程得解为正数,
∴-4k+3>0,
解得:k< .
故选C.
5.C
【分析】根据点的坐标,可得一元一次不等式组,根据解一元一次不等式,可得不等式组的解集,可得答案.
【详解】∵点P(2a 1,1 a)在第一象限,
∴,
解得,
∴,
故选C
【点睛】本题考查了点的坐标及在数轴上表示不等式组的解集:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
6.D
【分析】分别解出各个不等式的解集,再根据题意写出不等式组的解题即可.
【详解】①;②,解得:x>4; ③,解得:x<2; ④,解得:x<3;
A:①与②组合解集为:x>4,不符合题意;
B:②与③组合,无解,不符合题意;
C:③与④组合解集为:x<2,不符合题意;
D:①与④组合解集为:1故选:D
【点睛】本题主要考查了一元一次不等式组得解法,熟练地根据不等式的性质解不等式,并且能够写出不等式组的解集是解题的关键.
7.B
【分析】先解不等式②得,然后分不等式组有解和无解两种情况求解即可.
【详解】解:
解不等式②得:,
当不等式组有解集时,
∴不等式组的解集为,
∵关于的不等式组至多有4个整数解,
∴,
解得,
当不等式组无解时,即,
∴综上所述,,
故选B.
【点睛】本题主要考查了根据不等式组的解集情况求参数,利用分类讨论的思想求解是解题的关键.
8.A
【分析】由题干中信息可得“不超过”即“≤”,“不低于”即“≥”,于是30岁的年龄最佳燃脂心率范围用不等式表示为114≤p≤152.
【详解】 最佳燃脂心率最高值不应该超过(220-年龄)×0.8,,
p≤144
最佳燃脂心率最低值不低于(220-年龄)×0.6,,
108≤p
在四个选项中只有A选项正确.
故选: A.
【点睛】本题主要考查不等式的简单应用,能将体现不等关系的文字语言转化为数学语言是解决题目的关键.体现不等关系的文字语言有“大于”、“小于”、“不高于”、“不低于”等.
9.
【分析】根据题意列出不等式求解即可.
【详解】解:根据题意得:≤
-2x≤8
,
故答案为:.
【点睛】本题考查了解一元一次不等式,解题关键是根据题意列出不等式.
10.
【分析】利用有理数除法法则:同号得正,异号得负.可判断当代数式的值是非负数时,,解不等式即可求出x的范围.
【详解】解:∵的值是非负数,即
∴,
解不等式得:
故答案为:
【点睛】本题考查了解不等式和有理数除法运算法则,能够熟练运用运算法则及熟练解不等式是解题的关键.
11.
【分析】首先解不等式求的不等式的解集,然后确定解集中的最小整数值,代入方程求得a的值即可;
【详解】解不等式,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得,
则最小的整数解为-2.
把代入中,
得,
解得:.
故答案为.
【点睛】本题主要考查了一元一次方程的解与一元一次不等式的整数解,准确计算是解题的关键.
12.度
【分析】结合数轴,找出公共部分即可.
【详解】如图:阴影部分即为所求,
故答案为:度
【点睛】本题主要考查了找不等式组的解集,结合数轴可以快速准确地找出不等式组的解集,熟练地运用数轴是解题的关键.
13.0
【分析】先解出一元一次不等式解集,根据解集判断出a和b的值,最后代入求出即可.
【详解】由x-a解得x,
由b-3x>0解得x<,
所以a+2<x<,
因为,
所以a+2=-1,=1,
所以a=-3,b=3,
因此0,
故答案是0.
【点睛】本题考查根据一元一次不等式组的解集情况求参数,代数式求值,本题解题的关键是根据解集确定未知数的值.
14.(1)2;(2)26;(3)
【分析】(1)利用方法二来求的值;由题意可知;
(2)先根据方法二的基本步骤求出,即可得;
(3)通过方法二得出,再利用不等式的性质进行求解.
【详解】解:(1)利用方法二来求的值;
由题意可知:,
即;
(2)对于方程组,
由①②可得:,
则,
由③④可得:,
,
将代入④可得,
,
则;
(3)已知,
通过方法二计算得:
,
又,
.
【点睛】本题考查了二元一次方程的求解、代数式的求值、不等式的性质,解题的关键是理解材料中的方法二中的基本操作步骤.
15.(1)每瓶甲种消毒液的价格是30元,每瓶乙种消毒液的价格是40元;(2)最多能购买甲种消毒液55瓶.
【分析】(1)设每瓶甲种消毒液的价格是x元,每瓶乙种消毒液的价格是y元,根据“第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元”列出方程组求解即可;
(2)设可以购买甲种消毒液a瓶,根据“总花费不超过3 500元”列出不等式求解即可.
【详解】解:(1)设每瓶甲种消毒液的价格是x元,每瓶乙种消毒液的价格是y元.
依题意得:
解得:.
答:每瓶甲种消毒液的价格是30元,每瓶乙种消毒液的价格是40元.
(2)设可以购买甲种消毒液a瓶,则购买乙种消毒液(a-10)瓶.
依题意得:30a+40(a-10)≤3500.
解得:a≤
∴a的最大整数解为55.
答:最多能购买甲种消毒液55瓶.
【点睛】本题考查了二元一次方程组和一元一次不等式的实际应用,解决本题的关键是读懂题意,找到符合题意的等量关系和不等关系式.
16.(1)生产甲型口罩15万只,乙型口罩5万只.
(2)该医药公司四月份最多只能生产甲种防疫口罩17万只
(3)当购买数量少于280只时,选项方案一购买更实惠;当购买数量等于280只时,选择两种方案所需费用相同;当购买数量多于280只时,选择方案二购买更实惠.
【分析】(1)设生产甲型口罩x万只,乙型口罩y万只,利用销售总价=销售单价×销售数量,结合该公司三月份生产两种口罩20万只且全部售出后获得的销售收入为300万元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设生产甲型口罩m万只,则生产乙型口罩(20-m)万只,根据该公司四月份投入成本不超过216万元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(3)设购买乙型口罩a只,则选择方案一所需费用为5.4a元,选项方案二所需费用为(168+4.8a)元,分5.4a<168+4.8a,5.4a=168+4.8a及5.4a>168+4.8a三种情况,可求出a的取值范围(或a的值),进而可得出结论.
(1)解:设生产甲型口罩x万只,乙型口罩y万只,依题意得:,解得:.答:生产甲型口罩15万只,乙型口罩5万只.
(2)解:设生产甲型口罩m万只,则生产乙型口罩(20-m)万只,依题意得:12m+4(20-m)≤216,解得:m≤17.答:该医药公司四月份最多只能生产甲种防疫口罩17万只.
(3)设购买乙型口罩a只,则选择方案一所需费用为6×0.9a=5.4a(元),选项方案二所需费用为168+6×0.8a=(168+4.8a)(元).当5.4a<168+4.8a时,a<280;当5.4a=168+4.8a时,a=280;当5.4a>168+4.8a时,a>280.答:当购买数量少于280只时,选项方案一购买更实惠;当购买数量等于280只时,选择两种方案所需费用相同;当购买数量多于280只时,选择方案二购买更实惠.
【点睛】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是根据题意列出方程组或不等式组.
17.(1)
(2)或
(3)N(-4,m+3),
【分析】(1)利用非负性建立方程组,求出a,b,即可得出结论;
(2)先求出AC,AB,再分两种情况,利用运动表示出OD,OE,进而表示出△AOD和△AOE的面积,建立不等式求解,即可得出结论;
(3)根据点到点的平移方式,同样的方法可得到平移至,则根据点的坐标即可求解.
(1)
解:∵,
∴
(2)
由(1)知,A(4,3),
∵AB⊥x轴于B,AC⊥y轴于C,
∴AC=4,AB=3,
根据题意知,OD=t,OE=2t,
当点E在OB上时,即0<t<2,则OE=4-2t,
∵S△AOD<S△AOE,
∴2t<3(2-t),
当点E在BO的延长线上时,即t>2,
则OE=2t-4,
∵S△AOD<S△AOE,
∴2t<3(t-2),
∴t>6,
综上所述,或
(3)
点到点的平移方式为先向左平移4个单位,再向上平移3个单位,
由平移的性质得,点向左平移4个单位,再向上平移3个单位,得到点,
M(0,m)
N(-4,m+3),
【点睛】本题考查了非负数的性质,坐标与图形,一元一次不等式的应用,平移的性质,掌握以上知识是解题的关键.
18.x≤1,在数轴上表示解集见解析
【分析】求出每个不等式的解集,根据找不等式组解集的方法得出不等式组的解集,最后在数轴上表示出来即可.
【详解】解:,
解不等式①得:x≤1,
解不等式②得:x<4,
∴不等式组的解集为x≤1,
在数轴上表示解集为:
【点睛】本题考查了解一元一次不等式组,在数轴上表示不等式(或组)的解集,解此题的关键是能求出不等式组的解集,难度适中.
19.,-1、这两个数是该不等式组的解
【分析】先分别解两个不等式,得不等式组的解集,再判断两个数是不是不等式组的解即可.
【详解】解:
解不等式(1)得,,
解不等式(2)得,x<3,
∴不等式组的解集为,
∵,
∴-1、这两个数是该不等式组的解.
【点睛】本题考查不等式组的解法,不等式组的解,以及实数的大小比较,解题关键是正确地解不等式组.
20.(1),把解集表示在数轴上见解析
(2);整数解为:0、1、2、3
【分析】(1)先通过去括号、移项、系数化为1求出不等式的解,从而求出不等式组的解集,再把解集在数轴上表示即可;
(2)先通过去括号、移项、系数化为1求出不等式的解,从而求出不等式组的解集,即可确定解集中的整数解.
【详解】(1)解:,
由①得:,
由②得:,
∴不等式组的解集为:,把不等式组的解集表示在数轴上如图所示:
(2)解:,
由①得:,即,
由②得:,
去括号得:,
移项得:,
∴不等式组的解集为:,
∴不等式组的解集中的整数解为:0、1、2、3.
【点睛】本题考查解一元一次不等式组、求一元一次不等式组的整数解、在数轴上表示一元一次不等式组解集的方法,熟练掌握口诀确定一元一次不等式组的解集是解题的关键.
21.0≤x≤3,6
【分析】分别求出不等式组中两不等式的解集,找出解集的公共部分确定出解集,找出整数解即可.
【详解】解:,
解不等式①得:x≤3,
解不等式②得:x≥0,
则不等式组的解集为0≤x≤3,
∴不等式组的整数解为0,1,2,3,
所以不等式组的整数解之和为0+1+2+3=6.
【点睛】此题考查了解一元一次不等式组,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.
22.(1)购进甲种用品100件,乙种用品80件
(2)甲种用品61件,乙种用品119件
【分析】(1)设购进甲种用品x件,乙种用品y件,根据“购进甲、乙两种抗疫用品共180件,且销售完这批抗疫用品后能获利1240元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进甲种用品m件,则购进乙种用品(180-m)件,根据“投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为正整数即可得出各购货方案,再利用总利润=销售每件的利润×销售数量,可分别求出3个购货方案可获得的利润,比较后即可得出结论.
【详解】(1)设购进甲种用品x件,乙种用品y件,
依题意得: ,
解得: .
答:购进甲种用品100件,乙种用品80件.
(2)设购进甲种用品m件,则购进乙种用品(180-m)件,
依题意得:
,
解得:60<m≤63,
又∵m为正整数,
∴m可以取61,62,63,
∴共有3种购货方案,
方案1:购进甲种用品61件,乙种用品119件;
方案2:购进甲种用品62件,乙种用品118件;
方案3:购进甲种用品63件,乙种用品117件.
方案1可获得的利润为(20-14)×61+(43-35)×119=1318(元);
方案2可获得的利润为(20-14)×62+(43-35)×118=1316(元);
方案3可获得的利润为(20-14)×63+(43-35)×117=1314(元).
∵1318>1316>1314,
∴获利最大的购货方案为:购进甲种用品61件,乙种用品119件.
【点睛】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
23.(1)快递员小李平均每送一件和平均每揽一件的提成各是1.5元和2元
(2)他平均每天的送件数是160件或161件或162件或163件或164件
【分析】(1)设快递员小李平均每送一件的提成是元,平均每揽一件的提成是元,列二元一次方程求解;
(2)设他平均每天的送件数是件,则他平均每天的揽件数是件,列不等式组求解.
(1)
解:设快递员小李平均每送一件的提成是元,平均每揽一件的提成是元,根据题意得:
,
解得,
答:快递员小李平均每送一件和平均每揽一件的提成各是1.5元和2元;
(2)
解:设他平均每天的送件数是件,则他平均每天的揽件数是件,根据题意得:
,
解得,
是正整数,
的值为160,161,162,163,164,
答:他平均每天的送件数是160件或161件或162件或163件或164件.
【点睛】此题考查了二元一次方程组的实际应用,一元一次不等式组的实际应用,正确理解题意是解题的关键.
24.(1)A、B两种型号电风扇的销售单价分别为200元、150元;(2)超市最多采购A种型号电风扇37台;超市能实现利润超过1850元的目标,相应方案有两种:采购A种型号的电风扇36台,B种型号的电风扇14台;采购A种型号的电风扇37台,B种型号的电风扇13台
【分析】(1)设A种型号电风扇的销售单价为元,B种型号电风扇的销售单价为元.然后根据题意列二元一次方程组求解即可;
(2)设采购A种型号电风扇台,则采购B种型号电风扇台,然后根据“超市准备用不多于7500元”列不等式求出a的取值范围,进而确定购买两种电风扇的台数;然后再结合“超市销售完这50台电风扇能实现利润超过1850元”列不等式,进一步缩小a的取值范围,进而确定采购方案.
【详解】解:(1)设A种型号电风扇的销售单价为元,B种型号电风扇的销售单价为元.
依题意得:,解得:
答:A、B两种型号电风扇的销售单价分别为200元、150元;
(2)设采购A种型号电风扇台,则采购B种型号电风扇台.
依题意得:
解得:
所以超市最多采购A种型号电风扇37台时,采购金额不多于7500元;
又超市销售完这50台电风扇能实现利润超过1850元
则,解得:,
∵,且应为整数,
∴的值可取36、37.
所以超市能实现利润超过1850元的目标.相应方案有两种:
①采购A种型号的电风扇36台,B种型号的电风扇14台;
②采购A种型号的电风扇37台,B种型号的电风扇13台.
【点睛】本题主要考查了二元一次方程组的应用、一元一次不等式的应用,弄清题意、列出了二元一次方程组和一元一次不等式是解答本题的关键.
25.(1)草莓每亩平均收入3万元,葡萄每亩平均收入2.5万元
(2)种植方案为:种植草莓5亩,种植葡萄10亩;种植草莓6亩,种植葡萄9亩;种植草莓7亩,种植葡萄8亩.
【分析】(1)根据等量关系:甲种植户总收入为14万元,乙种植户总收入为18.5万元,列出方程组求解即可;
(2)设种植草莓的面积是亩,则种植葡萄的面积是亩,根据总收入不低于40万元,且种植草莓的面积不超过种植葡萄的面积(两类水果的种植面积均为整数),列不等式组求解,然后找出种植方案.
【详解】(1)解:设草莓每亩平均收入万元,葡萄每亩平均收入万元.
由题意得:,
解得:,
答:草莓每亩平均收入3万元,葡萄每亩平均收入2.5万元.
(2)解:设种植草莓的面积是亩,则种植葡萄的面积是亩.
由题意得:,
解得:.
为整数,
取:5、6、7.
种植方案为:种植草莓5亩,种植葡萄10亩;
种植草莓6亩,种植葡萄9亩;
种植草莓7亩,种植葡萄8亩.
【点睛】本题考查了二元一次方程组和一元一次不等式组的应用,读懂题意,找出合适的等量关系和不等关系是解题的关键.
一、单选题
1.(2022春·内蒙古呼伦贝尔·七年级统考期末)与5的和不大于,用不等式表示为( )
A. B. C. D.
2.(2022春·内蒙古乌兰察布·七年级统考期末)以下所给的数值中,为不等式﹣2x+3<0的解的是( )
A.﹣2 B.﹣1 C. D.2
3.(2022春·内蒙古呼伦贝尔·七年级统考期末)若,则下列不等式中正确的是( )
A. B. C. D.
4.(2022春·内蒙古通辽·七年级统考期末)若关于x的方程x﹣2+3k=的解是正数,则k的取值范围是( )
A.k> B.k≥ C.k< D.k≤
5.(2022春·内蒙古兴安盟·七年级统考期末)已知点P(2a 1,1 a)在第一象限,则a的取值范围在数轴上表示正确的是
A. B. C. D.
6.(2022春·内蒙古呼和浩特·七年级统考期末)已知不等式:①,②,③,④,从这四个不等式中取两个,构成正整数解是2的不等式组是( )
A.①与② B.②与③ C.③与④ D.①与④
7.(2022春·内蒙古通辽·七年级统考期末)若关于的不等式组至多有4个整数解,则的取值范围是( )
A. B. C. D.
8.(2022春·内蒙古兴安盟·七年级统考期末)研究表明,运动时将心率p(次)控制在最佳燃脂心率范围内,能起到燃烧脂肪并且保护心脏功能的作用.最佳燃脂心率最高值不应该超过(220﹣年龄)×0.8,最低值不低于(220﹣年龄)×0.6.以40岁为例计算,220﹣40=180,180×0.8=144,180×0.6=108,所以40岁的年龄最佳燃脂心率的范围用不等式可表示为( )
A.108≤p≤144 B.108<p<144 C.108≤p≤190 D.108<p<190
二、填空题
9.(2022春·内蒙古通辽·七年级统考期末)当_________时,式子的值不大于的值.
10.(2022春·内蒙古巴彦淖尔·七年级统考期末)当x满足_______时,代数式的值是非负数.
11.(2022春·内蒙古巴彦淖尔·七年级统考期末)已知满足不等式的最小整数解是方程的解,则的值为________.
12.(2022春·内蒙古呼和浩特·七年级统考期末)A、B两种花卉的最佳生长温度t分别是度和度,若把这两种花卉放在一起种植,请用不等式表示最佳的生长温度t应控制在范围________.
13.(2022春·内蒙古通辽·七年级统考期末)若不等式组 解集是-1
14.(2022春·内蒙古兴安盟·七年级统考期末)【发现问题】已知,求的值.
方法一:先解方程组,得出,的值,再代入,求出的值.
方法二:将①②,求出的值.
【提出问题】怎样才能得到方法二呢?
【分析问题】
为了得到方法二,可以将①②,可得.
令等式左边,比较系数可得,求得.
【解决问题】
(1)请你选择一种方法,求的值;
(2)对于方程组利用方法二的思路,求的值;
【迁移应用】
(3)已知,求的范围.
15.(2022春·内蒙古乌兰察布·七年级统考期末)某学校为了防控新型冠状病毒,购买了甲、乙两种消毒液进行校园环境消毒.已知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元.
(1)每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元
(2)学校准备第三次购买这两种消毒液,其中甲种消毒液比乙种消毒液多10瓶,并且总花费不超过3 500元,最多能购买多少瓶甲种消毒液
16.(2022春·内蒙古鄂尔多斯·七年级统考期末)随着新冠疫情的出现,口罩成为日常生活的必需品,某医药公司每月生产甲、乙两种型号的防疫口罩共20万只,且所有口罩当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/只 4元/只
售价 18元/只 6元/只
(1)若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?
(2)如果该公司四月份投入成本不超过216万元,该医药公司四月份最多只能生产甲种防疫口罩多少万只?
(3)某学校到该公司购买乙型口罩有如下两种方案,方案一:乙型口罩一律打9折;方案二:购买168元会员卡后,乙型口罩一律8折.请帮学校设计出合适的购买方案.
17.(2022春·内蒙古鄂尔多斯·七年级统考期末)如图1,平面甶角坐标系中,点A在第一象限,轴于B,轴于C,,且a,b满足.
(1)直接写出点A的坐标________.
(2)如图2,点D从点O出发以每秒1个单位的速度沿射线OC方向运动,点E从点B出发,以每秒2个单位的速度沿射线BO方向运动,设运动时间为t,当三角形AOD的面积小于三角形AOE的面积时,求t的取值范围;
(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点N落在第二象限,设点M的坐标为,请直接用含m的式子表示点N的坐标.
18.(2022春·内蒙古呼伦贝尔·七年级统考期末)解下列不等式组,并把它的解集在数轴上表示出来:
19.(2022春·内蒙古巴彦淖尔·七年级统考期末)解不等式组,并判断-1、这两个数是不是该不等式组的解.
20.(2022春·内蒙古通辽·七年级统考期末)解不等式组
(1)(把它的解集表示在数轴上).
(2)(并写出它的整数解).
21.(2022春·内蒙古通辽·七年级统考期末)解不等式组并求出不等式组的整数解之和.
22.(2022春·内蒙古通辽·七年级统考期末)某商家欲购进甲、乙两种抗疫用品共180件,其进价和售价如表:
甲 乙
进价(元/件) 14 35
售价(元/件) 20 43
(1)若商家计划销售完这批抗疫用品后能获利1240元,问甲、乙两种用品应分别购进多少件?(请用二元一次方程组求解)
(2)若商家计划投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
23.(2022春·内蒙古呼和浩特·七年级统考期末)快递员把货物送到客户手中称为送件,帮客户寄出货物称为揽件.快递员的提成取决于送件数和揽件数.某快递公司快递员小李若平均每天的送件数和揽件数分别为80件和20件,则他平均每天的提成是160元;若平均每天的送件数和揽件数分别为120件和25件,则他平均每天的提成是230元
(1)求快递员小李平均每送一件和平均每揽一件的提成各是多少元;
(2)已知快递员小李一周内平均每天的送件数和揽件数共计200件,且揽件数不大于送件数的.如果他平均每天的提成不低于318,求他平均每天的送件数.
24.(2022春·内蒙古呼伦贝尔·七年级统考期末)某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 4台 1200元
第二周 5台 6台 1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?若超市销售完这50台电风扇能实现利润超过1850元的目标,请直接给出相应的采购方案.
25.(2022春·内蒙古兴安盟·七年级统考期末)甲、乙两种植户,他们均种植了草莓,葡萄两类水果,两种植户种植的两类水果的种植面积与总收入如下表:
种植户 种植草莓面积(单位:亩) 种植葡萄面积(单位:亩) 总收入(单位:万元)
甲 3 2 14
乙 2 5 18.5
说明:不同种植户种植的同类水果每亩平均收入相等.
(1)求草莓、葡萄两类水果每亩平均收入各是多少万元?
(2)某种植户准备租15亩地用来种植草莓、葡萄两类水果,为了使总收入不低于40万元,且种植草莓的面积不超过种植葡萄的面积(两类水果的种植面积均为整数),求该种植户所有种植方案.
参考答案:
1.D
【分析】读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式,不大于即小于或等于.
【详解】解:“与5的和不大于-1”用不等式表示为,
故选:D.
【点睛】此题考查利用字母来表示题目中的不等关系,抓住大于、小于、不大于、不小于等关键字.
2.D
【详解】解:-2x<-3,x>,
∴不等式的解集是:x>.
故选D.
3.A
【分析】根据不等式的性质逐项判断即得答案.
【详解】解:A、若,则,故本选项变形正确,符合题意;
B、若,则,故本选项变形错误,不符合题意;
C、若,则,故本选项变形错误,不符合题意;
D、若,则,故本选项变形错误,不符合题意.
故选:A.
【点睛】本题考查了不等式的性质,属于基础题型,熟练掌握不等式的性质是解题关键.
4.C
【详解】解方程x﹣2+3k=得:x=-4k+3,
∵方程得解为正数,
∴-4k+3>0,
解得:k< .
故选C.
5.C
【分析】根据点的坐标,可得一元一次不等式组,根据解一元一次不等式,可得不等式组的解集,可得答案.
【详解】∵点P(2a 1,1 a)在第一象限,
∴,
解得,
∴,
故选C
【点睛】本题考查了点的坐标及在数轴上表示不等式组的解集:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
6.D
【分析】分别解出各个不等式的解集,再根据题意写出不等式组的解题即可.
【详解】①;②,解得:x>4; ③,解得:x<2; ④,解得:x<3;
A:①与②组合解集为:x>4,不符合题意;
B:②与③组合,无解,不符合题意;
C:③与④组合解集为:x<2,不符合题意;
D:①与④组合解集为:1
【点睛】本题主要考查了一元一次不等式组得解法,熟练地根据不等式的性质解不等式,并且能够写出不等式组的解集是解题的关键.
7.B
【分析】先解不等式②得,然后分不等式组有解和无解两种情况求解即可.
【详解】解:
解不等式②得:,
当不等式组有解集时,
∴不等式组的解集为,
∵关于的不等式组至多有4个整数解,
∴,
解得,
当不等式组无解时,即,
∴综上所述,,
故选B.
【点睛】本题主要考查了根据不等式组的解集情况求参数,利用分类讨论的思想求解是解题的关键.
8.A
【分析】由题干中信息可得“不超过”即“≤”,“不低于”即“≥”,于是30岁的年龄最佳燃脂心率范围用不等式表示为114≤p≤152.
【详解】 最佳燃脂心率最高值不应该超过(220-年龄)×0.8,,
p≤144
最佳燃脂心率最低值不低于(220-年龄)×0.6,,
108≤p
在四个选项中只有A选项正确.
故选: A.
【点睛】本题主要考查不等式的简单应用,能将体现不等关系的文字语言转化为数学语言是解决题目的关键.体现不等关系的文字语言有“大于”、“小于”、“不高于”、“不低于”等.
9.
【分析】根据题意列出不等式求解即可.
【详解】解:根据题意得:≤
-2x≤8
,
故答案为:.
【点睛】本题考查了解一元一次不等式,解题关键是根据题意列出不等式.
10.
【分析】利用有理数除法法则:同号得正,异号得负.可判断当代数式的值是非负数时,,解不等式即可求出x的范围.
【详解】解:∵的值是非负数,即
∴,
解不等式得:
故答案为:
【点睛】本题考查了解不等式和有理数除法运算法则,能够熟练运用运算法则及熟练解不等式是解题的关键.
11.
【分析】首先解不等式求的不等式的解集,然后确定解集中的最小整数值,代入方程求得a的值即可;
【详解】解不等式,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得,
则最小的整数解为-2.
把代入中,
得,
解得:.
故答案为.
【点睛】本题主要考查了一元一次方程的解与一元一次不等式的整数解,准确计算是解题的关键.
12.度
【分析】结合数轴,找出公共部分即可.
【详解】如图:阴影部分即为所求,
故答案为:度
【点睛】本题主要考查了找不等式组的解集,结合数轴可以快速准确地找出不等式组的解集,熟练地运用数轴是解题的关键.
13.0
【分析】先解出一元一次不等式解集,根据解集判断出a和b的值,最后代入求出即可.
【详解】由x-a解得x,
由b-3x>0解得x<,
所以a+2<x<,
因为,
所以a+2=-1,=1,
所以a=-3,b=3,
因此0,
故答案是0.
【点睛】本题考查根据一元一次不等式组的解集情况求参数,代数式求值,本题解题的关键是根据解集确定未知数的值.
14.(1)2;(2)26;(3)
【分析】(1)利用方法二来求的值;由题意可知;
(2)先根据方法二的基本步骤求出,即可得;
(3)通过方法二得出,再利用不等式的性质进行求解.
【详解】解:(1)利用方法二来求的值;
由题意可知:,
即;
(2)对于方程组,
由①②可得:,
则,
由③④可得:,
,
将代入④可得,
,
则;
(3)已知,
通过方法二计算得:
,
又,
.
【点睛】本题考查了二元一次方程的求解、代数式的求值、不等式的性质,解题的关键是理解材料中的方法二中的基本操作步骤.
15.(1)每瓶甲种消毒液的价格是30元,每瓶乙种消毒液的价格是40元;(2)最多能购买甲种消毒液55瓶.
【分析】(1)设每瓶甲种消毒液的价格是x元,每瓶乙种消毒液的价格是y元,根据“第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元”列出方程组求解即可;
(2)设可以购买甲种消毒液a瓶,根据“总花费不超过3 500元”列出不等式求解即可.
【详解】解:(1)设每瓶甲种消毒液的价格是x元,每瓶乙种消毒液的价格是y元.
依题意得:
解得:.
答:每瓶甲种消毒液的价格是30元,每瓶乙种消毒液的价格是40元.
(2)设可以购买甲种消毒液a瓶,则购买乙种消毒液(a-10)瓶.
依题意得:30a+40(a-10)≤3500.
解得:a≤
∴a的最大整数解为55.
答:最多能购买甲种消毒液55瓶.
【点睛】本题考查了二元一次方程组和一元一次不等式的实际应用,解决本题的关键是读懂题意,找到符合题意的等量关系和不等关系式.
16.(1)生产甲型口罩15万只,乙型口罩5万只.
(2)该医药公司四月份最多只能生产甲种防疫口罩17万只
(3)当购买数量少于280只时,选项方案一购买更实惠;当购买数量等于280只时,选择两种方案所需费用相同;当购买数量多于280只时,选择方案二购买更实惠.
【分析】(1)设生产甲型口罩x万只,乙型口罩y万只,利用销售总价=销售单价×销售数量,结合该公司三月份生产两种口罩20万只且全部售出后获得的销售收入为300万元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设生产甲型口罩m万只,则生产乙型口罩(20-m)万只,根据该公司四月份投入成本不超过216万元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(3)设购买乙型口罩a只,则选择方案一所需费用为5.4a元,选项方案二所需费用为(168+4.8a)元,分5.4a<168+4.8a,5.4a=168+4.8a及5.4a>168+4.8a三种情况,可求出a的取值范围(或a的值),进而可得出结论.
(1)解:设生产甲型口罩x万只,乙型口罩y万只,依题意得:,解得:.答:生产甲型口罩15万只,乙型口罩5万只.
(2)解:设生产甲型口罩m万只,则生产乙型口罩(20-m)万只,依题意得:12m+4(20-m)≤216,解得:m≤17.答:该医药公司四月份最多只能生产甲种防疫口罩17万只.
(3)设购买乙型口罩a只,则选择方案一所需费用为6×0.9a=5.4a(元),选项方案二所需费用为168+6×0.8a=(168+4.8a)(元).当5.4a<168+4.8a时,a<280;当5.4a=168+4.8a时,a=280;当5.4a>168+4.8a时,a>280.答:当购买数量少于280只时,选项方案一购买更实惠;当购买数量等于280只时,选择两种方案所需费用相同;当购买数量多于280只时,选择方案二购买更实惠.
【点睛】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是根据题意列出方程组或不等式组.
17.(1)
(2)或
(3)N(-4,m+3),
【分析】(1)利用非负性建立方程组,求出a,b,即可得出结论;
(2)先求出AC,AB,再分两种情况,利用运动表示出OD,OE,进而表示出△AOD和△AOE的面积,建立不等式求解,即可得出结论;
(3)根据点到点的平移方式,同样的方法可得到平移至,则根据点的坐标即可求解.
(1)
解:∵,
∴
(2)
由(1)知,A(4,3),
∵AB⊥x轴于B,AC⊥y轴于C,
∴AC=4,AB=3,
根据题意知,OD=t,OE=2t,
当点E在OB上时,即0<t<2,则OE=4-2t,
∵S△AOD<S△AOE,
∴2t<3(2-t),
当点E在BO的延长线上时,即t>2,
则OE=2t-4,
∵S△AOD<S△AOE,
∴2t<3(t-2),
∴t>6,
综上所述,或
(3)
点到点的平移方式为先向左平移4个单位,再向上平移3个单位,
由平移的性质得,点向左平移4个单位,再向上平移3个单位,得到点,
M(0,m)
N(-4,m+3),
【点睛】本题考查了非负数的性质,坐标与图形,一元一次不等式的应用,平移的性质,掌握以上知识是解题的关键.
18.x≤1,在数轴上表示解集见解析
【分析】求出每个不等式的解集,根据找不等式组解集的方法得出不等式组的解集,最后在数轴上表示出来即可.
【详解】解:,
解不等式①得:x≤1,
解不等式②得:x<4,
∴不等式组的解集为x≤1,
在数轴上表示解集为:
【点睛】本题考查了解一元一次不等式组,在数轴上表示不等式(或组)的解集,解此题的关键是能求出不等式组的解集,难度适中.
19.,-1、这两个数是该不等式组的解
【分析】先分别解两个不等式,得不等式组的解集,再判断两个数是不是不等式组的解即可.
【详解】解:
解不等式(1)得,,
解不等式(2)得,x<3,
∴不等式组的解集为,
∵,
∴-1、这两个数是该不等式组的解.
【点睛】本题考查不等式组的解法,不等式组的解,以及实数的大小比较,解题关键是正确地解不等式组.
20.(1),把解集表示在数轴上见解析
(2);整数解为:0、1、2、3
【分析】(1)先通过去括号、移项、系数化为1求出不等式的解,从而求出不等式组的解集,再把解集在数轴上表示即可;
(2)先通过去括号、移项、系数化为1求出不等式的解,从而求出不等式组的解集,即可确定解集中的整数解.
【详解】(1)解:,
由①得:,
由②得:,
∴不等式组的解集为:,把不等式组的解集表示在数轴上如图所示:
(2)解:,
由①得:,即,
由②得:,
去括号得:,
移项得:,
∴不等式组的解集为:,
∴不等式组的解集中的整数解为:0、1、2、3.
【点睛】本题考查解一元一次不等式组、求一元一次不等式组的整数解、在数轴上表示一元一次不等式组解集的方法,熟练掌握口诀确定一元一次不等式组的解集是解题的关键.
21.0≤x≤3,6
【分析】分别求出不等式组中两不等式的解集,找出解集的公共部分确定出解集,找出整数解即可.
【详解】解:,
解不等式①得:x≤3,
解不等式②得:x≥0,
则不等式组的解集为0≤x≤3,
∴不等式组的整数解为0,1,2,3,
所以不等式组的整数解之和为0+1+2+3=6.
【点睛】此题考查了解一元一次不等式组,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.
22.(1)购进甲种用品100件,乙种用品80件
(2)甲种用品61件,乙种用品119件
【分析】(1)设购进甲种用品x件,乙种用品y件,根据“购进甲、乙两种抗疫用品共180件,且销售完这批抗疫用品后能获利1240元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进甲种用品m件,则购进乙种用品(180-m)件,根据“投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为正整数即可得出各购货方案,再利用总利润=销售每件的利润×销售数量,可分别求出3个购货方案可获得的利润,比较后即可得出结论.
【详解】(1)设购进甲种用品x件,乙种用品y件,
依题意得: ,
解得: .
答:购进甲种用品100件,乙种用品80件.
(2)设购进甲种用品m件,则购进乙种用品(180-m)件,
依题意得:
,
解得:60<m≤63,
又∵m为正整数,
∴m可以取61,62,63,
∴共有3种购货方案,
方案1:购进甲种用品61件,乙种用品119件;
方案2:购进甲种用品62件,乙种用品118件;
方案3:购进甲种用品63件,乙种用品117件.
方案1可获得的利润为(20-14)×61+(43-35)×119=1318(元);
方案2可获得的利润为(20-14)×62+(43-35)×118=1316(元);
方案3可获得的利润为(20-14)×63+(43-35)×117=1314(元).
∵1318>1316>1314,
∴获利最大的购货方案为:购进甲种用品61件,乙种用品119件.
【点睛】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
23.(1)快递员小李平均每送一件和平均每揽一件的提成各是1.5元和2元
(2)他平均每天的送件数是160件或161件或162件或163件或164件
【分析】(1)设快递员小李平均每送一件的提成是元,平均每揽一件的提成是元,列二元一次方程求解;
(2)设他平均每天的送件数是件,则他平均每天的揽件数是件,列不等式组求解.
(1)
解:设快递员小李平均每送一件的提成是元,平均每揽一件的提成是元,根据题意得:
,
解得,
答:快递员小李平均每送一件和平均每揽一件的提成各是1.5元和2元;
(2)
解:设他平均每天的送件数是件,则他平均每天的揽件数是件,根据题意得:
,
解得,
是正整数,
的值为160,161,162,163,164,
答:他平均每天的送件数是160件或161件或162件或163件或164件.
【点睛】此题考查了二元一次方程组的实际应用,一元一次不等式组的实际应用,正确理解题意是解题的关键.
24.(1)A、B两种型号电风扇的销售单价分别为200元、150元;(2)超市最多采购A种型号电风扇37台;超市能实现利润超过1850元的目标,相应方案有两种:采购A种型号的电风扇36台,B种型号的电风扇14台;采购A种型号的电风扇37台,B种型号的电风扇13台
【分析】(1)设A种型号电风扇的销售单价为元,B种型号电风扇的销售单价为元.然后根据题意列二元一次方程组求解即可;
(2)设采购A种型号电风扇台,则采购B种型号电风扇台,然后根据“超市准备用不多于7500元”列不等式求出a的取值范围,进而确定购买两种电风扇的台数;然后再结合“超市销售完这50台电风扇能实现利润超过1850元”列不等式,进一步缩小a的取值范围,进而确定采购方案.
【详解】解:(1)设A种型号电风扇的销售单价为元,B种型号电风扇的销售单价为元.
依题意得:,解得:
答:A、B两种型号电风扇的销售单价分别为200元、150元;
(2)设采购A种型号电风扇台,则采购B种型号电风扇台.
依题意得:
解得:
所以超市最多采购A种型号电风扇37台时,采购金额不多于7500元;
又超市销售完这50台电风扇能实现利润超过1850元
则,解得:,
∵,且应为整数,
∴的值可取36、37.
所以超市能实现利润超过1850元的目标.相应方案有两种:
①采购A种型号的电风扇36台,B种型号的电风扇14台;
②采购A种型号的电风扇37台,B种型号的电风扇13台.
【点睛】本题主要考查了二元一次方程组的应用、一元一次不等式的应用,弄清题意、列出了二元一次方程组和一元一次不等式是解答本题的关键.
25.(1)草莓每亩平均收入3万元,葡萄每亩平均收入2.5万元
(2)种植方案为:种植草莓5亩,种植葡萄10亩;种植草莓6亩,种植葡萄9亩;种植草莓7亩,种植葡萄8亩.
【分析】(1)根据等量关系:甲种植户总收入为14万元,乙种植户总收入为18.5万元,列出方程组求解即可;
(2)设种植草莓的面积是亩,则种植葡萄的面积是亩,根据总收入不低于40万元,且种植草莓的面积不超过种植葡萄的面积(两类水果的种植面积均为整数),列不等式组求解,然后找出种植方案.
【详解】(1)解:设草莓每亩平均收入万元,葡萄每亩平均收入万元.
由题意得:,
解得:,
答:草莓每亩平均收入3万元,葡萄每亩平均收入2.5万元.
(2)解:设种植草莓的面积是亩,则种植葡萄的面积是亩.
由题意得:,
解得:.
为整数,
取:5、6、7.
种植方案为:种植草莓5亩,种植葡萄10亩;
种植草莓6亩,种植葡萄9亩;
种植草莓7亩,种植葡萄8亩.
【点睛】本题考查了二元一次方程组和一元一次不等式组的应用,读懂题意,找出合适的等量关系和不等关系是解题的关键.
