第七章:平面直角坐标系练习题(含解析)2021-2022学年内蒙古各地七年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第七章:平面直角坐标系练习题(含解析)2021-2022学年内蒙古各地七年级下学期人教版数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 688.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 14:57:05 | ||
图片预览



文档简介
第七章:平面直角坐标系 练习题
一、单选题
1.(2022春·内蒙古巴彦淖尔·七年级统考期末)已知,点 P 在第四象限,且点 P 到 x 轴、y 轴的距离分别为 3 和 4,则点 P 的坐标为( )
A.(-3,4) B.(3,-4) C.(-4,3) D.(4,-3)
2.(2022春·内蒙古呼和浩特·七年级统考期末)如图,小手盖住的点的坐标可能为( )
A. B. C. D.
3.(2022春·内蒙古乌兰察布·七年级统考期末) 已知点P(0,m)在y轴的负半轴上,则点M( m, m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2022春·内蒙古通辽·七年级统考期末)在平面直角坐标系中,点(﹣1,m2+1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·内蒙古乌兰察布·七年级统考期末)在平面直角坐标系中,已知点M(m-1,2m+3)在y轴上,则m的值为( )
A.1 B.-1 C. D.
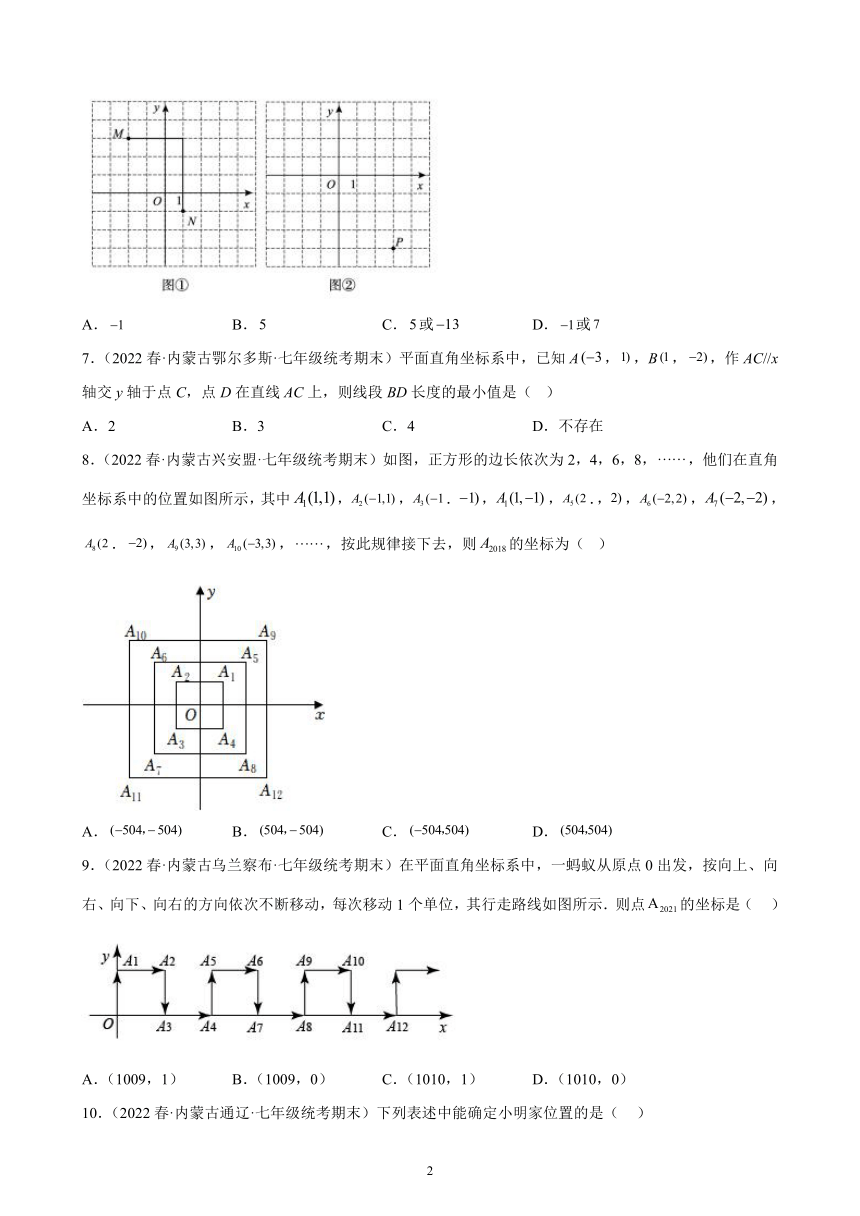
6.(2022春·内蒙古鄂尔多斯·七年级统考期末)我们规定:在平面直角坐标系中,任意不重合的两点,之间的折线距离为,例如图①中,点与点之间的折线距离为.如图②,已知点若点的坐标为,且,则的值为( )
A. B. C.或 D.或
7.(2022春·内蒙古鄂尔多斯·七年级统考期末)平面直角坐标系中,已知A,,B,,作AC//x轴交y轴于点C,点D在直线AC上,则线段BD长度的最小值是( )
A.2 B.3 C.4 D.不存在
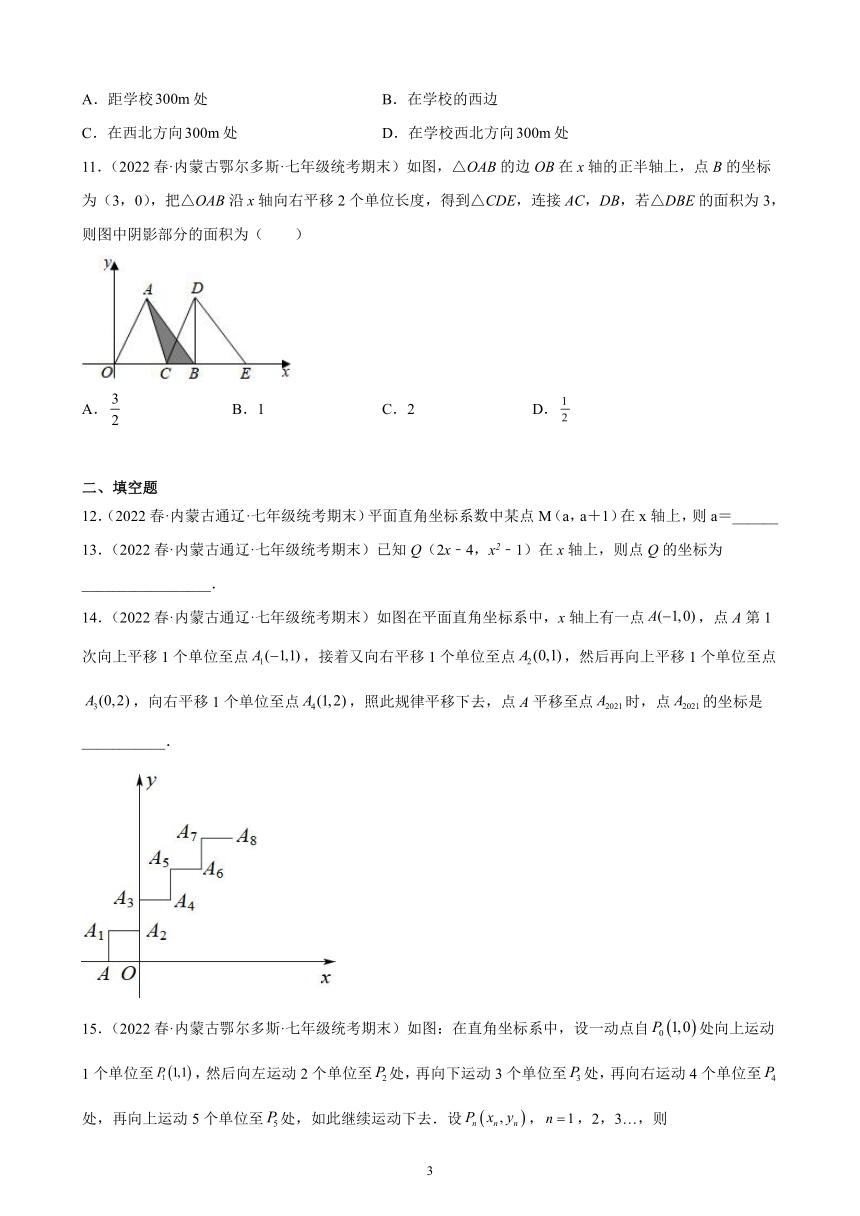
8.(2022春·内蒙古兴安盟·七年级统考期末)如图,正方形的边长依次为2,4,6,8,,他们在直角坐标系中的位置如图所示,其中,,.,,.,,,,.,,,,按此规律接下去,则的坐标为( )
A. B. C. D.
9.(2022春·内蒙古乌兰察布·七年级统考期末)在平面直角坐标系中,一蚂蚁从原点0出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点的坐标是( )
A.(1009,1) B.(1009,0) C.(1010,1) D.(1010,0)
10.(2022春·内蒙古通辽·七年级统考期末)下列表述中能确定小明家位置的是( )
A.距学校处 B.在学校的西边
C.在西北方向处 D.在学校西北方向处
11.(2022春·内蒙古鄂尔多斯·七年级统考期末)如图,△OAB的边OB在x轴的正半轴上,点B的坐标为(3,0),把△OAB沿x轴向右平移2个单位长度,得到△CDE,连接AC,DB,若△DBE的面积为3,则图中阴影部分的面积为( )
A. B.1 C.2 D.
二、填空题
12.(2022春·内蒙古通辽·七年级统考期末)平面直角坐标系数中某点M(a,a+1)在x轴上,则a=______
13.(2022春·内蒙古通辽·七年级统考期末)已知Q(2x﹣4,x2﹣1)在x轴上,则点Q的坐标为_________________.
14.(2022春·内蒙古通辽·七年级统考期末)如图在平面直角坐标系中,x轴上有一点,点A第1次向上平移1个单位至点,接着又向右平移1个单位至点,然后再向上平移1个单位至点,向右平移1个单位至点,照此规律平移下去,点A平移至点时,点的坐标是___________.
15.(2022春·内蒙古鄂尔多斯·七年级统考期末)如图:在直角坐标系中,设一动点自处向上运动1个单位至,然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,如此继续运动下去.设,,2,3…,则________.
16.(2022春·内蒙古呼和浩特·七年级统考期末)已知小薇的家的西方1000米处为车站,家的北方2000米处为学校,且从学校往东方走1000米,再往南走3000米可到达公园.若小薇将自己的家、车站、学校分别表示在坐标平面上的、、三点,则公园在此坐标平面上表示点的坐标为________.
17.(2022春·内蒙古兴安盟·七年级统考期末)如图是象棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4,-1)上,则“炮”所在的点可表示为__________.
18.(2022春·内蒙古通辽·七年级统考期末)如图,在平面直角坐标系中,点A1(1,2),A2(2,0),A3(3,-2),A4(4,0)……根据这个规律,探究可得点A2017的坐标是________.
三、解答题
19.(2022春·内蒙古乌兰察布·七年级统考期末)(1)如图,△ABC三个顶点的坐标分别为A(-3,5),B(-4,3),C(-1,1).
①画出△ABC向右平移5个单位长度,向下平移2个单位长度得到的△(不写画法)
②请直接写出,,的坐标;
③求△ABC的面积.
(2)已知,如图,在△ABC中,AH平分∠BAC交BC于点H、D、E分别在CA、BA的延长线上,DBAH,∠D=∠E.
求证:AHEC,
证明:∵DBAH,
∴∠D= ,( )
∵AH平分∠BAC,
∴ (角平分线定义)
∴∠D= ,(等量代换)
∵∠D=∠E,
∴ (等量代换)
∴AHEC( )
20.(2022春·内蒙古通辽·七年级统考期末)如图,A(﹣3,2),B(﹣1,﹣2),C(1,﹣1),将△ABC向右平移3个单位长度,然后再向上平移1个单位长度,可以得到△A1B1C1
(1)画出平移后的△A1B1C1,并写出A1,B1,C1的坐标;
(2)求△ABC的面积;
(3)在x轴上存在点P,使得△PA1C1面积为,求点P的坐标.
21.(2022春·内蒙古呼伦贝尔·七年级统考期末)如图,在平面直角坐标系中,已知A( 2,2),B(2,0),C(3,3),P(a,b)是三角形ABC的边AC上的一点,三角形ABC经过平移后得到三角形DEF,点P的对应点为P′(a 2,b 4).
(1)请画出三角形DEF,并写出三角形DEF的三个顶点坐标;
(2)求三角形ABC的面积;
(3) x轴上是否存在点Q,使得三角形ABQ的面积是4?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
22.(2022春·内蒙古兴安盟·七年级统考期末)如图,在平面直角坐标系xOy中,已知P(1,2).
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
23.(2022春·内蒙古呼和浩特·七年级统考期末)按要求作图、解答
(1)请在网格中建立平面直角坐标系,使得A,B两点的坐标分别为,;
(2)在(1)的条件下,平移线段AB使点A移动到点C,点B移动到点D画出平移后的线段CD,并直接写出点D的坐标.
24.(2022春·内蒙古巴彦淖尔·七年级统考期末)如图,已知在网格图中,每个小正方形的边长都是1.
(1)在图中若,,请写出点C的坐标;
(2)在(1)的基础上,把沿边平移,使点A移到点C,变换为,请你在图中画出,并写出D、E两点的坐标;
(3)求的面积.
参考答案:
1.D
【分析】应先判断出点P的横纵坐标的符号,进而根据到坐标轴的距离判断其具体坐标.
【详解】解:∵第四象限内的点横坐标大于0,纵坐标小于0;点P到x轴的距离是3,到y轴的距离为4,
∴点P的纵坐标为:-3,横坐标为:4,
∴点P的坐标是:(4,-3).
故选D.
【点睛】本题考查了点到坐标轴的距离,点到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值.注意第四象限的点的符号特点是(+,-).
2.A
【分析】根据各个象限内的点的坐标特征逐一判断即可.
【详解】由图可知,小手盖住的点的坐标位于第三象限,
,,,中,只有在第三象限,
所以,小手盖住的点的坐标可能为.
故选:A.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
3.A
【详解】点P(0,m)在y轴的负半轴上,
∴m<0,
∴-m>0,-m+1>0,
∴点M(-m,-m+1)在第一象限;
故选:A
4.B
【分析】应先判断出点的横纵坐标的符号,进而判断点所在的象限.
【详解】解:因为点(﹣1,m2+1),横坐标﹣1<0,纵坐标m2+1一定大于0,
所以满足点在第二象限的条件.
故选:B
【点睛】本题主要考查平面直角坐标系里象限的坐标,熟练掌握每个象限的坐标符号特点是解题的关键.
5.A
【分析】根据在y轴上的点横坐标为0求解.
【详解】解:根据在y轴上的点横坐标为0,得:m-1=0,
解得m=1.
故选:A.
【点睛】此题考查了点与坐标的对应关系,熟记坐标轴上的点的特征是解答本题的关键.
6.D
【分析】根据折线距离的定义可得关于t的绝对值方程,解方程即可求出t的值,进而可得答案.
【详解】解:∵,点的坐标为,,
∴,
解得:或.
故选:D.
【点睛】本题考查了坐标与图形,正确理解折线距离、掌握绝对值方程的解法是解题的关键.
7.B
【分析】先画出符合题意的图形,再根据“点到直线的距离垂线段最短”可得到答案.
【详解】解:如图,AC//x轴交y轴于点C,点D在直线AC上,
时,最小,
A,,B,,
∴D(1,1),
此时:
故选:B.
【点睛】本题考查的是坐标与图形,点到直线的距离,垂线段最短,掌握以上知识是解题的关键.
8.C
【分析】由正方形的中心都是位于原点,边长依次为2,4,6,8,,可得第个正方形的顶点横坐标与纵坐标的绝对值都是.计算,根据商和余数知道是第几个正方形的顶点,且在哪一个象限,进而得出的坐标.
【详解】解:,
顶点是第504个正方形的顶点,且在第二象限,
横坐标是,纵坐标是504,
,
故选:C.
【点睛】本题主要考查对正方形的性质,坐标与图形性质,能根据已知找出规律是解题的关键.
9.C
【分析】根据点列A5、A9、A13、…的规律,即可求出A2021的坐标.
【详解】解:由图可知A5(2,1),A9(4,1),A13(6,1),…,
根据规律可知A的下标为5、9、13、…,
即第n个数可以用4n+1表示,
点的纵坐标依次为2、4、6、…,
即第n个数为2n,
∴点列A5、A9、A13、…的第n个点为A4n+1(2n,1),
当4n+1=2021时,n=505,
∴A2021(1010,1),
故选:C.
【点睛】本题主要考查点的规律变化,关键是要仔细观察图像,得出点的变化规律.
10.D
【分析】根据确定具体位置需要三个元素进行判断即可得出结果.
【详解】解:A、只有距离无方向和观测点,不能确定具体位置,选项不符合题意;
B、只有方向无距离和观测点,不能确定具体位置,选项不符合题意;
C、有距离和方向,无观测点,不能确定具体位置,选项不符合题意;
D、既有距离又有方向、观测点,可以确定具体位置,符合题意;
故选:D.
【点睛】题目主要考查确定具体位置的方法,掌握确定具体位置的方法是解题关键.
11.A
【分析】设A(m,n),利用三角形面积公式求出n的值,再求出BC,可得结论.
【详解】解:设A(m,n),
∵B(3,0),
∴OB=3,
由平移的性质可知,OC=BE=2,
∴BC=OB﹣OC=1,
∵S△DBE=×2×n=3,
∴n=3,
∴S△ACB=×1×3=,
故选:A.
【点睛】本题考查了坐标与图形变化-平移,三角形的面积等知识点,解题的关键是求出点A的纵坐标.
12.-1
【分析】根据x轴上的点纵坐标等于0列出方程求解得到a的值.
【详解】∵点M(a,a+1)在x轴上,
∴a+1=0,
解得a=-1,
故答案为:-1.
【点睛】本题考查了点的坐标,熟记x轴上的点的纵坐标等于0是解题的关键.
13.(﹣2,0)或(﹣6,0)
【分析】根据x轴上的点的纵坐标为0可得x的值,进而得出2x﹣4的值,从而得出点Q的坐标.
【详解】解:∵Q(2x﹣4,x2﹣1)在x轴上,
∴x2﹣1=0,
解得x=±1,
当x=1时,2x﹣4=﹣2,
当x=﹣1时,2x﹣4=﹣6,
故点Q的坐标为(﹣2,0)或(﹣6,0).
故答案为:(﹣2,0)或(﹣6,0).
【点睛】本题考查了点的坐标,熟知x轴上的点的纵坐标为0是解答本题的关键.
14.
【分析】探究规律,利用规律解决问题即可.
【详解】解:由题意,A1( 1,1),
A3(0,2),
A5(1,3),
A7(2,4),
,
A2n 1( 2+n,n),
当时,,
∴A2021(1009,1011).
故答案为:(1009,1011).
【点睛】本题主要考查了坐标与图形变化 平移,解题的关键是学会探究规律的方法,属于中考常考题型.
15.1010
【分析】根据各点横坐标数据得出规律,进而得出x1+x2+…+x7;经过观察分析可得每4个数的和为2,把2020个数分为505组,然后根据规律得到x2021, x2022的值分别为:1011,-1011,即可得到答案.
【详解】解:根据平面坐标系结合各点横坐标得出:x1、x2、x3、x4、x5、x6、x7、x8的值分别为:1,-1,-1,3,3,-3,-3,5;
∵x1+x2+x3+x4=1-1-1+3=2,
x5+x6+x7+x8=3-3-3+5=2,
…,
以此类推,可以得到,从第一项开始,每四项的和都是2,
∴x1+x2+…+x2020=2×(2020÷4)=1010.
又∵x2021, x2022的值分别为:1011,-1011
x2021+x2022=1011-1011=0
∴x1+x2+…+x2022=1010
故答案为:1010
【点睛】此题主要考查了点的坐标特点,解决本题的关键是分析得到4个数相加的规律.
16.
【分析】根据住家、车站、学校分别标示在坐标平面上的(2,0)、(0,0)、(2,4)三点建立坐标系,然后求出每单位的实际长度,根据题目给的信息即可解答.
【详解】解:在坐标平面上标示出住家(2,0)、车站(0,0),学校(2,4)三点,
∵小薇住家的西方1000米处为车站,
∴每1单位长是1000÷2=500(米).
∵从学校往东方走1000米,再往南走3000米可到达公园.
∴在坐标平面上要从学校(2,4)往东1000÷500=2单位长,再往南3000÷500=6单位长可到达公园.
∴公园(2+2,4-6),
即(4,-2).
故答案为:(4,-2).
【点睛】本题考查了坐标确定位置,根据已知条件画出图形是解决问题的关键,由图形可直观地解答.
17.(-1,2)
【详解】解:根据“帅”位于点(2,-1)上,“相”位于点(4,-1)上,可知棋盘中一个格代表一个单位,“炮”所在的点在帅左面3个单位,上面3个单位,故坐标是(-1,2).
故答案为(-1,2).
18.(2017,2)
【详解】分析:由图形得出点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是0、2、0、-2、0、2、0、-2、…,四个一循环,继而求得答案.
详解:观察图形可知,
点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是0、2、0、 2、0、2、0、 2、…,四个一循环,
2017÷4=504…1,
故点A2017坐标是(2017,2).
故答案为(2017,2).
点睛:本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解本题的关键是根据图形得出规律.
19.(1)①见解析; ②(2,3),(1,1),(4,-1);③△ABC的面积为4;(2)∠CAH;两直线平行,同位角相等;∠BAH=∠CAH;∠BAH;∠E=∠BAH;同位角相等,两直线平行
【分析】(1)①利用平移变换的性质分别作出A,B,C的对应点,,即可;
②根据点的位置写出坐标即可;
③把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
(2)由平行线的性质可得∠D=∠CAH,再由角平分线的定义得∠BAH=∠CAH,从而得∠D=∠BAH,即可求得∠E=∠BAH,可判定AHEC.
【详解】(1)解:①如图,△即为所求;
②(2,3),(1,1),(4,-1);
③△ABC的面积=3×4-×2×3-×1×2-×2×4=4;
(2)证明:∵DBAH,
∴∠D=∠CAH(两直线平行,同位角相等),
∵AH平分∠BAC,
∴∠BAH=∠CAH(角平分线定义),
∴∠D=∠BAH(等量代换),
∵∠D=∠E,
∴∠E=∠BAH(等量代换),
∴AHEC(同位角相等,两直线平行)
故答案为:∠CAH;两直线平行,同位角相等;∠BAH=∠CAH;∠BAH;∠E=∠BAH;同位角相等,两直线平行.
【点睛】本题主要考查作图-平移变换,三角形的面积,平行线的判定与性质,解答的关键是熟记平行线的判定定理及性质并灵活运用.
20.(1)画图见解析,
(2)5
(3)或
【分析】(1)先分别确定平移后的对应点 再顺次连接即可,根据点在坐标系内的位置可得点的坐标.
(2)利用△ABC所在的长方形减去周围三个直角三角形即可得出答案.
(3)设 可得 再利用面积公式列绝对值方程即可.
【详解】(1)解:如图,△A1B1C1即为所求;
(2)△ABC的面积为
(3)设
解得:或
或
【点睛】本题主要考查了作图-平移变换,平面直角坐标系中点的坐标的特征,三角形的面积等知识,准确画出图形是解题的关键.
21.(1)画出△DEF见解析,D(-4,-2);E(0,-4); F(1,-1);
(2)△DEF的面积为7;
(3)Q(6,0)或Q(-2,0).
【分析】(1)直接利用对应点变化规律进而分别得出对应点位置;
(2)利用△DEF所在三角形面积减去周围三角形面积即可得出答案;
(3)设Q(m,0),由三角形面积得出方程,解方程即可.
(1)
解:∵P 为 AC 上的点,P 平移后 P (a-2,b-4)表示向左平移2个单位,再向下平移 4 个单位.
如图所示,△DEF即为所作.
∴D(-4,-2);E(0,-4); F(1,-1);
(2)
解:△DEF的面积为:3×5-×1×5-×2×4-×1×3
=15--4-
=7;
(3)
解:设Q(m,0),
∵A(-2,2),B(2,0),
∴BQ=|2-m|,
∵△ABQ的面积为4,
∴×2×|2-m |=4,
解得:m=6或-2,
∴Q(6,0)或Q(-2,0).
【点睛】此题主要考查了平移变换以及三角形面积求法,正确得出对应点的位置是解题关键.
22.(1)点P的位置如图所示,见解析;(2)点P'的坐标为(﹣2,3);(3)点A的坐标为(0,4)或(0,﹣4)或(2,0)或(﹣2,0).
【分析】(1)根据题意画出点P即可;
(2)根据平移的性质得出坐标即可;
(3)根据三角形的面积公式解答即可.
【详解】(1)点P的位置如图所示,
(2)将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为(﹣2,3),
故填:(﹣2,3);
(3)∵点A在坐标轴上,S△OAP=2,
当点A在x轴上时,△OAP的高为2,故OA的长为2,∴(2,0)或(﹣2,0).
当点A在y轴上时,△OAP的高为1,故OA的长为4,∴(0,4)或(0,﹣4).
∴点A的坐标为(0,4)或(0,﹣4)或(2,0)或(﹣2,0).
【点睛】此题考查坐标与图形,关键是根据平移的性质解答.
23.(1)见解析;
(2)见解析;点D的坐标为.
【分析】(1)根据点的坐标选择合适的坐标系即可;
(2)根据点的平移特点求解即可.
(1)
解:如图所示,建立平面直角坐标系:
(2)
解:平移后的线段CD如图所示,
∵移动到,可理解为:向上平移1个单位,再向左平移2个单位,
∴向上平移1个单位,再向左平移2个单位得到.
【点睛】本题考查直角坐标系,坐标点平移的特点,解题的关键是数形结合进行建立坐标系,掌握点的平移特点.
24.(1)
(2)画图见解析,
(3)12
【分析】(1)如图,以A为坐标原点,过A的两条互相垂直的网格线作为坐标轴建立坐标系,再根据C在坐标系内的位置可得答案;
(2)由点A移到点C,即图形先向右平移4个单位,再向上平移4个单位,再分别确定B,C的对应点E,D,再顺次连接C,D,E即可;
(3)直接利用三角形的面积公式进行计算即可.
(1)解:如图,以A为坐标原点,过A的两条互相垂直的网格线作为坐标轴建立坐标系,∴
(2)如图,即为所求作的三角形;∴
(3)
【点睛】本题考查的是坐标与图形,平移的作图,三角形的面积的计算,熟练的根据平移的性质进行作图是解本题的关键.
一、单选题
1.(2022春·内蒙古巴彦淖尔·七年级统考期末)已知,点 P 在第四象限,且点 P 到 x 轴、y 轴的距离分别为 3 和 4,则点 P 的坐标为( )
A.(-3,4) B.(3,-4) C.(-4,3) D.(4,-3)
2.(2022春·内蒙古呼和浩特·七年级统考期末)如图,小手盖住的点的坐标可能为( )
A. B. C. D.
3.(2022春·内蒙古乌兰察布·七年级统考期末) 已知点P(0,m)在y轴的负半轴上,则点M( m, m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2022春·内蒙古通辽·七年级统考期末)在平面直角坐标系中,点(﹣1,m2+1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·内蒙古乌兰察布·七年级统考期末)在平面直角坐标系中,已知点M(m-1,2m+3)在y轴上,则m的值为( )
A.1 B.-1 C. D.
6.(2022春·内蒙古鄂尔多斯·七年级统考期末)我们规定:在平面直角坐标系中,任意不重合的两点,之间的折线距离为,例如图①中,点与点之间的折线距离为.如图②,已知点若点的坐标为,且,则的值为( )
A. B. C.或 D.或
7.(2022春·内蒙古鄂尔多斯·七年级统考期末)平面直角坐标系中,已知A,,B,,作AC//x轴交y轴于点C,点D在直线AC上,则线段BD长度的最小值是( )
A.2 B.3 C.4 D.不存在
8.(2022春·内蒙古兴安盟·七年级统考期末)如图,正方形的边长依次为2,4,6,8,,他们在直角坐标系中的位置如图所示,其中,,.,,.,,,,.,,,,按此规律接下去,则的坐标为( )
A. B. C. D.
9.(2022春·内蒙古乌兰察布·七年级统考期末)在平面直角坐标系中,一蚂蚁从原点0出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点的坐标是( )
A.(1009,1) B.(1009,0) C.(1010,1) D.(1010,0)
10.(2022春·内蒙古通辽·七年级统考期末)下列表述中能确定小明家位置的是( )
A.距学校处 B.在学校的西边
C.在西北方向处 D.在学校西北方向处
11.(2022春·内蒙古鄂尔多斯·七年级统考期末)如图,△OAB的边OB在x轴的正半轴上,点B的坐标为(3,0),把△OAB沿x轴向右平移2个单位长度,得到△CDE,连接AC,DB,若△DBE的面积为3,则图中阴影部分的面积为( )
A. B.1 C.2 D.
二、填空题
12.(2022春·内蒙古通辽·七年级统考期末)平面直角坐标系数中某点M(a,a+1)在x轴上,则a=______
13.(2022春·内蒙古通辽·七年级统考期末)已知Q(2x﹣4,x2﹣1)在x轴上,则点Q的坐标为_________________.
14.(2022春·内蒙古通辽·七年级统考期末)如图在平面直角坐标系中,x轴上有一点,点A第1次向上平移1个单位至点,接着又向右平移1个单位至点,然后再向上平移1个单位至点,向右平移1个单位至点,照此规律平移下去,点A平移至点时,点的坐标是___________.
15.(2022春·内蒙古鄂尔多斯·七年级统考期末)如图:在直角坐标系中,设一动点自处向上运动1个单位至,然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,如此继续运动下去.设,,2,3…,则________.
16.(2022春·内蒙古呼和浩特·七年级统考期末)已知小薇的家的西方1000米处为车站,家的北方2000米处为学校,且从学校往东方走1000米,再往南走3000米可到达公园.若小薇将自己的家、车站、学校分别表示在坐标平面上的、、三点,则公园在此坐标平面上表示点的坐标为________.
17.(2022春·内蒙古兴安盟·七年级统考期末)如图是象棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4,-1)上,则“炮”所在的点可表示为__________.
18.(2022春·内蒙古通辽·七年级统考期末)如图,在平面直角坐标系中,点A1(1,2),A2(2,0),A3(3,-2),A4(4,0)……根据这个规律,探究可得点A2017的坐标是________.
三、解答题
19.(2022春·内蒙古乌兰察布·七年级统考期末)(1)如图,△ABC三个顶点的坐标分别为A(-3,5),B(-4,3),C(-1,1).
①画出△ABC向右平移5个单位长度,向下平移2个单位长度得到的△(不写画法)
②请直接写出,,的坐标;
③求△ABC的面积.
(2)已知,如图,在△ABC中,AH平分∠BAC交BC于点H、D、E分别在CA、BA的延长线上,DBAH,∠D=∠E.
求证:AHEC,
证明:∵DBAH,
∴∠D= ,( )
∵AH平分∠BAC,
∴ (角平分线定义)
∴∠D= ,(等量代换)
∵∠D=∠E,
∴ (等量代换)
∴AHEC( )
20.(2022春·内蒙古通辽·七年级统考期末)如图,A(﹣3,2),B(﹣1,﹣2),C(1,﹣1),将△ABC向右平移3个单位长度,然后再向上平移1个单位长度,可以得到△A1B1C1
(1)画出平移后的△A1B1C1,并写出A1,B1,C1的坐标;
(2)求△ABC的面积;
(3)在x轴上存在点P,使得△PA1C1面积为,求点P的坐标.
21.(2022春·内蒙古呼伦贝尔·七年级统考期末)如图,在平面直角坐标系中,已知A( 2,2),B(2,0),C(3,3),P(a,b)是三角形ABC的边AC上的一点,三角形ABC经过平移后得到三角形DEF,点P的对应点为P′(a 2,b 4).
(1)请画出三角形DEF,并写出三角形DEF的三个顶点坐标;
(2)求三角形ABC的面积;
(3) x轴上是否存在点Q,使得三角形ABQ的面积是4?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
22.(2022春·内蒙古兴安盟·七年级统考期末)如图,在平面直角坐标系xOy中,已知P(1,2).
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
23.(2022春·内蒙古呼和浩特·七年级统考期末)按要求作图、解答
(1)请在网格中建立平面直角坐标系,使得A,B两点的坐标分别为,;
(2)在(1)的条件下,平移线段AB使点A移动到点C,点B移动到点D画出平移后的线段CD,并直接写出点D的坐标.
24.(2022春·内蒙古巴彦淖尔·七年级统考期末)如图,已知在网格图中,每个小正方形的边长都是1.
(1)在图中若,,请写出点C的坐标;
(2)在(1)的基础上,把沿边平移,使点A移到点C,变换为,请你在图中画出,并写出D、E两点的坐标;
(3)求的面积.
参考答案:
1.D
【分析】应先判断出点P的横纵坐标的符号,进而根据到坐标轴的距离判断其具体坐标.
【详解】解:∵第四象限内的点横坐标大于0,纵坐标小于0;点P到x轴的距离是3,到y轴的距离为4,
∴点P的纵坐标为:-3,横坐标为:4,
∴点P的坐标是:(4,-3).
故选D.
【点睛】本题考查了点到坐标轴的距离,点到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值.注意第四象限的点的符号特点是(+,-).
2.A
【分析】根据各个象限内的点的坐标特征逐一判断即可.
【详解】由图可知,小手盖住的点的坐标位于第三象限,
,,,中,只有在第三象限,
所以,小手盖住的点的坐标可能为.
故选:A.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
3.A
【详解】点P(0,m)在y轴的负半轴上,
∴m<0,
∴-m>0,-m+1>0,
∴点M(-m,-m+1)在第一象限;
故选:A
4.B
【分析】应先判断出点的横纵坐标的符号,进而判断点所在的象限.
【详解】解:因为点(﹣1,m2+1),横坐标﹣1<0,纵坐标m2+1一定大于0,
所以满足点在第二象限的条件.
故选:B
【点睛】本题主要考查平面直角坐标系里象限的坐标,熟练掌握每个象限的坐标符号特点是解题的关键.
5.A
【分析】根据在y轴上的点横坐标为0求解.
【详解】解:根据在y轴上的点横坐标为0,得:m-1=0,
解得m=1.
故选:A.
【点睛】此题考查了点与坐标的对应关系,熟记坐标轴上的点的特征是解答本题的关键.
6.D
【分析】根据折线距离的定义可得关于t的绝对值方程,解方程即可求出t的值,进而可得答案.
【详解】解:∵,点的坐标为,,
∴,
解得:或.
故选:D.
【点睛】本题考查了坐标与图形,正确理解折线距离、掌握绝对值方程的解法是解题的关键.
7.B
【分析】先画出符合题意的图形,再根据“点到直线的距离垂线段最短”可得到答案.
【详解】解:如图,AC//x轴交y轴于点C,点D在直线AC上,
时,最小,
A,,B,,
∴D(1,1),
此时:
故选:B.
【点睛】本题考查的是坐标与图形,点到直线的距离,垂线段最短,掌握以上知识是解题的关键.
8.C
【分析】由正方形的中心都是位于原点,边长依次为2,4,6,8,,可得第个正方形的顶点横坐标与纵坐标的绝对值都是.计算,根据商和余数知道是第几个正方形的顶点,且在哪一个象限,进而得出的坐标.
【详解】解:,
顶点是第504个正方形的顶点,且在第二象限,
横坐标是,纵坐标是504,
,
故选:C.
【点睛】本题主要考查对正方形的性质,坐标与图形性质,能根据已知找出规律是解题的关键.
9.C
【分析】根据点列A5、A9、A13、…的规律,即可求出A2021的坐标.
【详解】解:由图可知A5(2,1),A9(4,1),A13(6,1),…,
根据规律可知A的下标为5、9、13、…,
即第n个数可以用4n+1表示,
点的纵坐标依次为2、4、6、…,
即第n个数为2n,
∴点列A5、A9、A13、…的第n个点为A4n+1(2n,1),
当4n+1=2021时,n=505,
∴A2021(1010,1),
故选:C.
【点睛】本题主要考查点的规律变化,关键是要仔细观察图像,得出点的变化规律.
10.D
【分析】根据确定具体位置需要三个元素进行判断即可得出结果.
【详解】解:A、只有距离无方向和观测点,不能确定具体位置,选项不符合题意;
B、只有方向无距离和观测点,不能确定具体位置,选项不符合题意;
C、有距离和方向,无观测点,不能确定具体位置,选项不符合题意;
D、既有距离又有方向、观测点,可以确定具体位置,符合题意;
故选:D.
【点睛】题目主要考查确定具体位置的方法,掌握确定具体位置的方法是解题关键.
11.A
【分析】设A(m,n),利用三角形面积公式求出n的值,再求出BC,可得结论.
【详解】解:设A(m,n),
∵B(3,0),
∴OB=3,
由平移的性质可知,OC=BE=2,
∴BC=OB﹣OC=1,
∵S△DBE=×2×n=3,
∴n=3,
∴S△ACB=×1×3=,
故选:A.
【点睛】本题考查了坐标与图形变化-平移,三角形的面积等知识点,解题的关键是求出点A的纵坐标.
12.-1
【分析】根据x轴上的点纵坐标等于0列出方程求解得到a的值.
【详解】∵点M(a,a+1)在x轴上,
∴a+1=0,
解得a=-1,
故答案为:-1.
【点睛】本题考查了点的坐标,熟记x轴上的点的纵坐标等于0是解题的关键.
13.(﹣2,0)或(﹣6,0)
【分析】根据x轴上的点的纵坐标为0可得x的值,进而得出2x﹣4的值,从而得出点Q的坐标.
【详解】解:∵Q(2x﹣4,x2﹣1)在x轴上,
∴x2﹣1=0,
解得x=±1,
当x=1时,2x﹣4=﹣2,
当x=﹣1时,2x﹣4=﹣6,
故点Q的坐标为(﹣2,0)或(﹣6,0).
故答案为:(﹣2,0)或(﹣6,0).
【点睛】本题考查了点的坐标,熟知x轴上的点的纵坐标为0是解答本题的关键.
14.
【分析】探究规律,利用规律解决问题即可.
【详解】解:由题意,A1( 1,1),
A3(0,2),
A5(1,3),
A7(2,4),
,
A2n 1( 2+n,n),
当时,,
∴A2021(1009,1011).
故答案为:(1009,1011).
【点睛】本题主要考查了坐标与图形变化 平移,解题的关键是学会探究规律的方法,属于中考常考题型.
15.1010
【分析】根据各点横坐标数据得出规律,进而得出x1+x2+…+x7;经过观察分析可得每4个数的和为2,把2020个数分为505组,然后根据规律得到x2021, x2022的值分别为:1011,-1011,即可得到答案.
【详解】解:根据平面坐标系结合各点横坐标得出:x1、x2、x3、x4、x5、x6、x7、x8的值分别为:1,-1,-1,3,3,-3,-3,5;
∵x1+x2+x3+x4=1-1-1+3=2,
x5+x6+x7+x8=3-3-3+5=2,
…,
以此类推,可以得到,从第一项开始,每四项的和都是2,
∴x1+x2+…+x2020=2×(2020÷4)=1010.
又∵x2021, x2022的值分别为:1011,-1011
x2021+x2022=1011-1011=0
∴x1+x2+…+x2022=1010
故答案为:1010
【点睛】此题主要考查了点的坐标特点,解决本题的关键是分析得到4个数相加的规律.
16.
【分析】根据住家、车站、学校分别标示在坐标平面上的(2,0)、(0,0)、(2,4)三点建立坐标系,然后求出每单位的实际长度,根据题目给的信息即可解答.
【详解】解:在坐标平面上标示出住家(2,0)、车站(0,0),学校(2,4)三点,
∵小薇住家的西方1000米处为车站,
∴每1单位长是1000÷2=500(米).
∵从学校往东方走1000米,再往南走3000米可到达公园.
∴在坐标平面上要从学校(2,4)往东1000÷500=2单位长,再往南3000÷500=6单位长可到达公园.
∴公园(2+2,4-6),
即(4,-2).
故答案为:(4,-2).
【点睛】本题考查了坐标确定位置,根据已知条件画出图形是解决问题的关键,由图形可直观地解答.
17.(-1,2)
【详解】解:根据“帅”位于点(2,-1)上,“相”位于点(4,-1)上,可知棋盘中一个格代表一个单位,“炮”所在的点在帅左面3个单位,上面3个单位,故坐标是(-1,2).
故答案为(-1,2).
18.(2017,2)
【详解】分析:由图形得出点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是0、2、0、-2、0、2、0、-2、…,四个一循环,继而求得答案.
详解:观察图形可知,
点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是0、2、0、 2、0、2、0、 2、…,四个一循环,
2017÷4=504…1,
故点A2017坐标是(2017,2).
故答案为(2017,2).
点睛:本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解本题的关键是根据图形得出规律.
19.(1)①见解析; ②(2,3),(1,1),(4,-1);③△ABC的面积为4;(2)∠CAH;两直线平行,同位角相等;∠BAH=∠CAH;∠BAH;∠E=∠BAH;同位角相等,两直线平行
【分析】(1)①利用平移变换的性质分别作出A,B,C的对应点,,即可;
②根据点的位置写出坐标即可;
③把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
(2)由平行线的性质可得∠D=∠CAH,再由角平分线的定义得∠BAH=∠CAH,从而得∠D=∠BAH,即可求得∠E=∠BAH,可判定AHEC.
【详解】(1)解:①如图,△即为所求;
②(2,3),(1,1),(4,-1);
③△ABC的面积=3×4-×2×3-×1×2-×2×4=4;
(2)证明:∵DBAH,
∴∠D=∠CAH(两直线平行,同位角相等),
∵AH平分∠BAC,
∴∠BAH=∠CAH(角平分线定义),
∴∠D=∠BAH(等量代换),
∵∠D=∠E,
∴∠E=∠BAH(等量代换),
∴AHEC(同位角相等,两直线平行)
故答案为:∠CAH;两直线平行,同位角相等;∠BAH=∠CAH;∠BAH;∠E=∠BAH;同位角相等,两直线平行.
【点睛】本题主要考查作图-平移变换,三角形的面积,平行线的判定与性质,解答的关键是熟记平行线的判定定理及性质并灵活运用.
20.(1)画图见解析,
(2)5
(3)或
【分析】(1)先分别确定平移后的对应点 再顺次连接即可,根据点在坐标系内的位置可得点的坐标.
(2)利用△ABC所在的长方形减去周围三个直角三角形即可得出答案.
(3)设 可得 再利用面积公式列绝对值方程即可.
【详解】(1)解:如图,△A1B1C1即为所求;
(2)△ABC的面积为
(3)设
解得:或
或
【点睛】本题主要考查了作图-平移变换,平面直角坐标系中点的坐标的特征,三角形的面积等知识,准确画出图形是解题的关键.
21.(1)画出△DEF见解析,D(-4,-2);E(0,-4); F(1,-1);
(2)△DEF的面积为7;
(3)Q(6,0)或Q(-2,0).
【分析】(1)直接利用对应点变化规律进而分别得出对应点位置;
(2)利用△DEF所在三角形面积减去周围三角形面积即可得出答案;
(3)设Q(m,0),由三角形面积得出方程,解方程即可.
(1)
解:∵P 为 AC 上的点,P 平移后 P (a-2,b-4)表示向左平移2个单位,再向下平移 4 个单位.
如图所示,△DEF即为所作.
∴D(-4,-2);E(0,-4); F(1,-1);
(2)
解:△DEF的面积为:3×5-×1×5-×2×4-×1×3
=15--4-
=7;
(3)
解:设Q(m,0),
∵A(-2,2),B(2,0),
∴BQ=|2-m|,
∵△ABQ的面积为4,
∴×2×|2-m |=4,
解得:m=6或-2,
∴Q(6,0)或Q(-2,0).
【点睛】此题主要考查了平移变换以及三角形面积求法,正确得出对应点的位置是解题关键.
22.(1)点P的位置如图所示,见解析;(2)点P'的坐标为(﹣2,3);(3)点A的坐标为(0,4)或(0,﹣4)或(2,0)或(﹣2,0).
【分析】(1)根据题意画出点P即可;
(2)根据平移的性质得出坐标即可;
(3)根据三角形的面积公式解答即可.
【详解】(1)点P的位置如图所示,
(2)将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为(﹣2,3),
故填:(﹣2,3);
(3)∵点A在坐标轴上,S△OAP=2,
当点A在x轴上时,△OAP的高为2,故OA的长为2,∴(2,0)或(﹣2,0).
当点A在y轴上时,△OAP的高为1,故OA的长为4,∴(0,4)或(0,﹣4).
∴点A的坐标为(0,4)或(0,﹣4)或(2,0)或(﹣2,0).
【点睛】此题考查坐标与图形,关键是根据平移的性质解答.
23.(1)见解析;
(2)见解析;点D的坐标为.
【分析】(1)根据点的坐标选择合适的坐标系即可;
(2)根据点的平移特点求解即可.
(1)
解:如图所示,建立平面直角坐标系:
(2)
解:平移后的线段CD如图所示,
∵移动到,可理解为:向上平移1个单位,再向左平移2个单位,
∴向上平移1个单位,再向左平移2个单位得到.
【点睛】本题考查直角坐标系,坐标点平移的特点,解题的关键是数形结合进行建立坐标系,掌握点的平移特点.
24.(1)
(2)画图见解析,
(3)12
【分析】(1)如图,以A为坐标原点,过A的两条互相垂直的网格线作为坐标轴建立坐标系,再根据C在坐标系内的位置可得答案;
(2)由点A移到点C,即图形先向右平移4个单位,再向上平移4个单位,再分别确定B,C的对应点E,D,再顺次连接C,D,E即可;
(3)直接利用三角形的面积公式进行计算即可.
(1)解:如图,以A为坐标原点,过A的两条互相垂直的网格线作为坐标轴建立坐标系,∴
(2)如图,即为所求作的三角形;∴
(3)
【点睛】本题考查的是坐标与图形,平移的作图,三角形的面积的计算,熟练的根据平移的性质进行作图是解本题的关键.
