人教版九年级下册数学期中试卷1(含答案)
文档属性
| 名称 | 人教版九年级下册数学期中试卷1(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 672.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 11:15:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2022-2023学年第二学期人教版九年级下册
期中测试数学试卷一
一、单选题(每小题3分,共30分)
1.的绝对值是( )
A.3 B. C. D.
2.某市计划在今后三年间植树造林1210000亩,全力打造绿色生态旅游城市,将1210000用科学记数法表示为( )
A. B. C. D.
3.观察下列图案,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
4.方程的解是( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.已知一个直角三角形的两边长分别为和,则第三边长是( )
A. B. C. D.或
7.直线y=kx+b经过一、二、四象限,则k、b应满足( )
A.k>0,b<0 B.k>0,b>0 C.k<0,b<0 D.k<0,b>0
8.如图是由个大小相同的正方体组成的几何体,它的左视图为( )
A. B. C. D.
9.实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.a>﹣2 B.b﹣a<0 C.a+b>0 D.|a|>b
10.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
二、填空题(每空2分,共24分)
11.计算:_____
12.分解因式:_____.
13.的平方根是 .
14.若单项式与单项式是同类项,则___________.
15.计算的结果是_____.
16.已知反比例函数,若x≥2,则y的取值范围为______.
17.已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m-n=______.
18.一元二次方程 x2﹣4x = 0 的解是_____________.
19. 若直线经过第一、三、四象限,则二次函数的图象顶点必在第__________象限.
20. 如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________ .
(第18题图) (第19题图)
21. 如图,从一块直径为的圆形铁皮上剪出一个圆心角为的扇形,则此扇形的面积为_____.
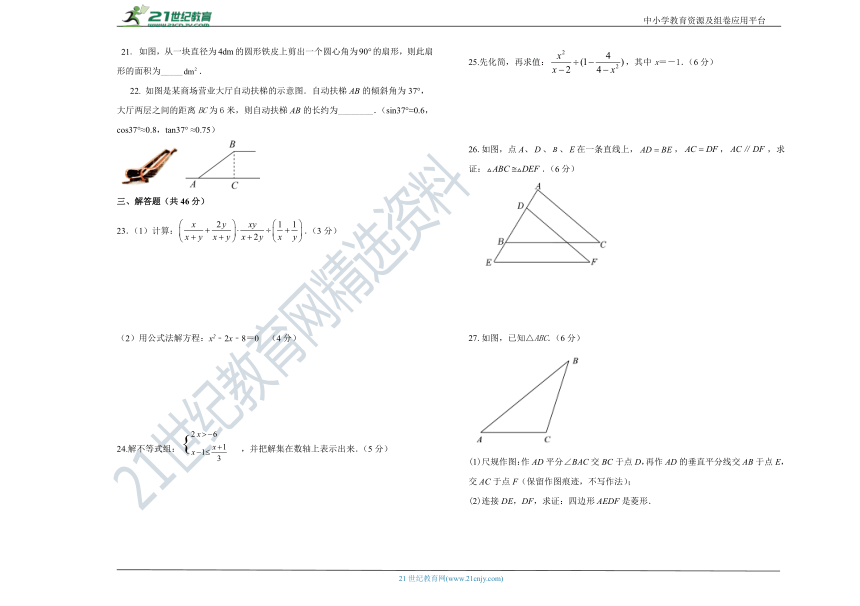
22. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为________.(sin37°≈0.6,cos37°≈0.8,tan37° ≈0.75)
解答题(共46分)
23.(1)计算:.(3分)
(2)用公式法解方程:x2﹣2x﹣8=0 (4分)
24.解不等式组:,并把解集在数轴上表示出来.(5分)
25.先化简,再求值:,其中x=-1.(6分)
26.如图,点A、、、在一条直线上,,,,求证:.(6分)
27.如图,已知△ABC.(6分)
(1)尺规作图:作AD平分∠BAC交BC于点D,再作AD的垂直平分线交AB于点E,交AC于点F(保留作图痕迹,不写作法);
(2)连接DE,DF,求证:四边形AEDF是菱形.
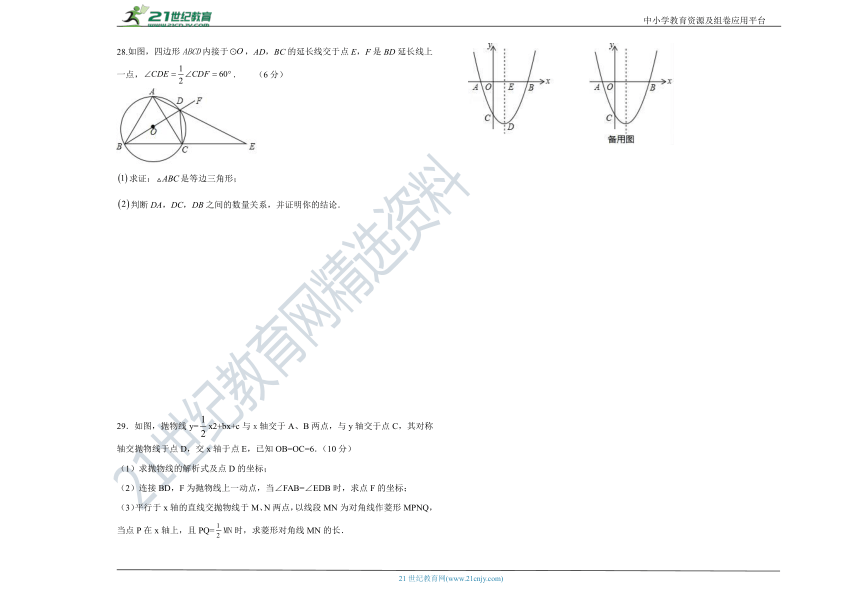
28.如图,四边形ABCD内接于,AD,BC的延长线交于点E,F是BD延长线上一点,. (6分)
求证:是等边三角形;
判断DA,DC,DB之间的数量关系,并证明你的结论.
29.如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.(10分)
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=MN时,求菱形对角线MN的长.
2022-2023学年第二学期人教版九年级下册
期中测试数学试卷一参考答案
一、单选题
1.C ; 2. D ; 3. C; 4. C ;5. B ;6. D ;7. D ; 8. B ; 9. D ; 10. B .
二、填空题
11. 12. ; 13. 14. 4 ;15. 16. 17. 7 ; 18. 19. 二 ;20. 4 ;21. 2Л ;22. 10 .
三、解答题
23.(1)计算:
(2)用公式法解方程:x2﹣2x﹣8=0
解:∵a=1 ,b=-2 ,c=-8 ,
∴
24.解不等式组
解:解不等式①得:x>-3 ,
解不等式②得:x≤2
所以不等式组的解集为:-3将不等式组的解集在数轴上表示如下:
25.先化简,再求值:,其中x=-1.
当x=-1时,原式=x+2=-1+2=1
26.如图,点A、、、在一条直线上,,,,求证:.
证明:在
∵点A、、、在一条直线上,(已知)
∴ AD+BD=BE+BD 即:AB=DE (等式的性质)
∵AC∥BE(已知) ∴∠EDF=∠A (两直线平行,同位角相等)
又∵AC=DF(已知) ∴ (SAS)
27.如图,已知△ABC.
(1)尺规作图:作AD平分∠BAC交BC于点D,再作AD的垂直平分线交AB于点E,交AC于点F(保留作图痕迹,不写作法);
(2)连接DE,DF,求证:四边形AEDF是菱形.
解:(1)尺规作图如图1:角平分线AD为所求作,垂直平分线EF为所求作。
图1 图2
(2)证明:连接DE,DF,
根据作法知:EF时线段AD的垂直平分线,
∴AE=DE AF=DF(线段垂直平分线上的点到线段两个端点的距离相等)
∴∠EAD=∠EDA (等角对等边)
∵ AD平分∠BAC(由作图知) ∴∠BAD=∠CAD ∴∠EDA=∠CAD
∴ DE∥AC(内错角相等,两直线平行)
同理可证:DF∥AB
∴四边形AFDE是平行四边形(两组对边分别平行的四边形是平行四边形)
又∵ AE=DE(已证)
∴ 平行四边形AFDE是菱形(一组邻边相等的平行四边形是菱形)
28.如图,四边形ABCD内接于,AD,BC的延长线交于点E,F是BD延长线上一点,.
求证:是等边三角形;
判断DA,DC,DB之间的数量关系,并证明你的结论.
证明:
∵四边形ABCD内接于 O,
由圆周角定理得:
29.如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=MN时,求菱形对角线MN的长.
解:(1)∵ OB=OC=6 , ∴ B(6,0),C(0,-6),
∴ 点D的坐标为(2,-8).
(2)如图1:过点F作
设F(x, ),则,
在中,令y=0,可得:,
∴ OA=2,则AG=x+2, ∵ B(6,0) D(2,-8)
∴ BE=6-2=4 ,DE=8 ,当∠FAB=∠EDB时,且∠FGA=∠BED,
~
当点F在x轴上方时,解得x=-2(舍去)或x=7 ,此时F点的坐标为
当点F在x轴下方时,解得x=-2(舍去)或x=5 ,此时F点的坐标为
综上可知F点的坐标为或
∵点P在x轴上,∴由菱形的对称性可知P(2,0),
如图2,当MN在x轴上方时,设T为菱形对角线的交点,
∵M在抛物线上,
,
当MN在x轴下方时,同理可设PT=n,则M(2+2n,-n),
综上可知菱形对角线MN的长为或
学 校
班 级
学 号
姓 名
座位号
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2022-2023学年第二学期人教版九年级下册
期中测试数学试卷一
一、单选题(每小题3分,共30分)
1.的绝对值是( )
A.3 B. C. D.
2.某市计划在今后三年间植树造林1210000亩,全力打造绿色生态旅游城市,将1210000用科学记数法表示为( )
A. B. C. D.
3.观察下列图案,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
4.方程的解是( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.已知一个直角三角形的两边长分别为和,则第三边长是( )
A. B. C. D.或
7.直线y=kx+b经过一、二、四象限,则k、b应满足( )
A.k>0,b<0 B.k>0,b>0 C.k<0,b<0 D.k<0,b>0
8.如图是由个大小相同的正方体组成的几何体,它的左视图为( )
A. B. C. D.
9.实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.a>﹣2 B.b﹣a<0 C.a+b>0 D.|a|>b
10.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
二、填空题(每空2分,共24分)
11.计算:_____
12.分解因式:_____.
13.的平方根是 .
14.若单项式与单项式是同类项,则___________.
15.计算的结果是_____.
16.已知反比例函数,若x≥2,则y的取值范围为______.
17.已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m-n=______.
18.一元二次方程 x2﹣4x = 0 的解是_____________.
19. 若直线经过第一、三、四象限,则二次函数的图象顶点必在第__________象限.
20. 如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________ .
(第18题图) (第19题图)
21. 如图,从一块直径为的圆形铁皮上剪出一个圆心角为的扇形,则此扇形的面积为_____.
22. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为________.(sin37°≈0.6,cos37°≈0.8,tan37° ≈0.75)
解答题(共46分)
23.(1)计算:.(3分)
(2)用公式法解方程:x2﹣2x﹣8=0 (4分)
24.解不等式组:,并把解集在数轴上表示出来.(5分)
25.先化简,再求值:,其中x=-1.(6分)
26.如图,点A、、、在一条直线上,,,,求证:.(6分)
27.如图,已知△ABC.(6分)
(1)尺规作图:作AD平分∠BAC交BC于点D,再作AD的垂直平分线交AB于点E,交AC于点F(保留作图痕迹,不写作法);
(2)连接DE,DF,求证:四边形AEDF是菱形.
28.如图,四边形ABCD内接于,AD,BC的延长线交于点E,F是BD延长线上一点,. (6分)
求证:是等边三角形;
判断DA,DC,DB之间的数量关系,并证明你的结论.
29.如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.(10分)
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=MN时,求菱形对角线MN的长.
2022-2023学年第二学期人教版九年级下册
期中测试数学试卷一参考答案
一、单选题
1.C ; 2. D ; 3. C; 4. C ;5. B ;6. D ;7. D ; 8. B ; 9. D ; 10. B .
二、填空题
11. 12. ; 13. 14. 4 ;15. 16. 17. 7 ; 18. 19. 二 ;20. 4 ;21. 2Л ;22. 10 .
三、解答题
23.(1)计算:
(2)用公式法解方程:x2﹣2x﹣8=0
解:∵a=1 ,b=-2 ,c=-8 ,
∴
24.解不等式组
解:解不等式①得:x>-3 ,
解不等式②得:x≤2
所以不等式组的解集为:-3
25.先化简,再求值:,其中x=-1.
当x=-1时,原式=x+2=-1+2=1
26.如图,点A、、、在一条直线上,,,,求证:.
证明:在
∵点A、、、在一条直线上,(已知)
∴ AD+BD=BE+BD 即:AB=DE (等式的性质)
∵AC∥BE(已知) ∴∠EDF=∠A (两直线平行,同位角相等)
又∵AC=DF(已知) ∴ (SAS)
27.如图,已知△ABC.
(1)尺规作图:作AD平分∠BAC交BC于点D,再作AD的垂直平分线交AB于点E,交AC于点F(保留作图痕迹,不写作法);
(2)连接DE,DF,求证:四边形AEDF是菱形.
解:(1)尺规作图如图1:角平分线AD为所求作,垂直平分线EF为所求作。
图1 图2
(2)证明:连接DE,DF,
根据作法知:EF时线段AD的垂直平分线,
∴AE=DE AF=DF(线段垂直平分线上的点到线段两个端点的距离相等)
∴∠EAD=∠EDA (等角对等边)
∵ AD平分∠BAC(由作图知) ∴∠BAD=∠CAD ∴∠EDA=∠CAD
∴ DE∥AC(内错角相等,两直线平行)
同理可证:DF∥AB
∴四边形AFDE是平行四边形(两组对边分别平行的四边形是平行四边形)
又∵ AE=DE(已证)
∴ 平行四边形AFDE是菱形(一组邻边相等的平行四边形是菱形)
28.如图,四边形ABCD内接于,AD,BC的延长线交于点E,F是BD延长线上一点,.
求证:是等边三角形;
判断DA,DC,DB之间的数量关系,并证明你的结论.
证明:
∵四边形ABCD内接于 O,
由圆周角定理得:
29.如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=MN时,求菱形对角线MN的长.
解:(1)∵ OB=OC=6 , ∴ B(6,0),C(0,-6),
∴ 点D的坐标为(2,-8).
(2)如图1:过点F作
设F(x, ),则,
在中,令y=0,可得:,
∴ OA=2,则AG=x+2, ∵ B(6,0) D(2,-8)
∴ BE=6-2=4 ,DE=8 ,当∠FAB=∠EDB时,且∠FGA=∠BED,
~
当点F在x轴上方时,解得x=-2(舍去)或x=7 ,此时F点的坐标为
当点F在x轴下方时,解得x=-2(舍去)或x=5 ,此时F点的坐标为
综上可知F点的坐标为或
∵点P在x轴上,∴由菱形的对称性可知P(2,0),
如图2,当MN在x轴上方时,设T为菱形对角线的交点,
∵M在抛物线上,
,
当MN在x轴下方时,同理可设PT=n,则M(2+2n,-n),
综上可知菱形对角线MN的长为或
学 校
班 级
学 号
姓 名
座位号
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
