2023届高考数学复习专题 ★★定点定值问题 课件(共110张PPT)
文档属性
| 名称 | 2023届高考数学复习专题 ★★定点定值问题 课件(共110张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 09:58:16 | ||
图片预览




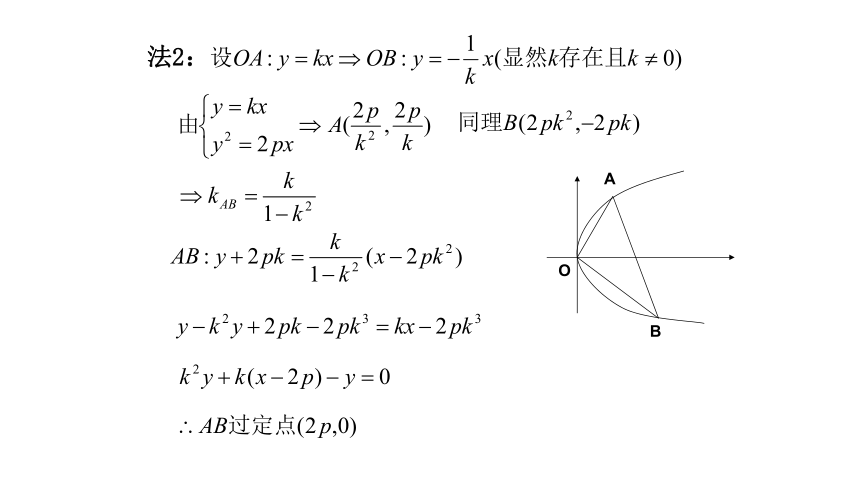



文档简介
(共110张PPT)
解析几何中的定量问题
2023届高考数学复习专题 ★★
一、定量问题的思想方法
思想方法:定量问题包括定点,定值,定角,定直线,
定面积等等。小题可以特殊化、极端化猜测得出,大
题则一般可以先猜再证。
能力要求:
(1)会猜——特殊化,极端化
(2)会证——
①设方程(直线通常为y=kx+b或x=my+n)
②联立方程组得关键方程
③转化几何条件建立代数关系
④利用韦达定理建立等式,统一参数字母
⑤求出定量
二、定点问题
例1、抛物线
(1)过原点 作两条互相垂直的弦 ,则直线
过定点为
O
A
B
解析:小题猜测:根据对称性,定点肯定在x轴上,
再取 ,易得
猜测定点
证:证明方法很多,这里略举几种,
后面的例题通法为主。
(一)抛物线类
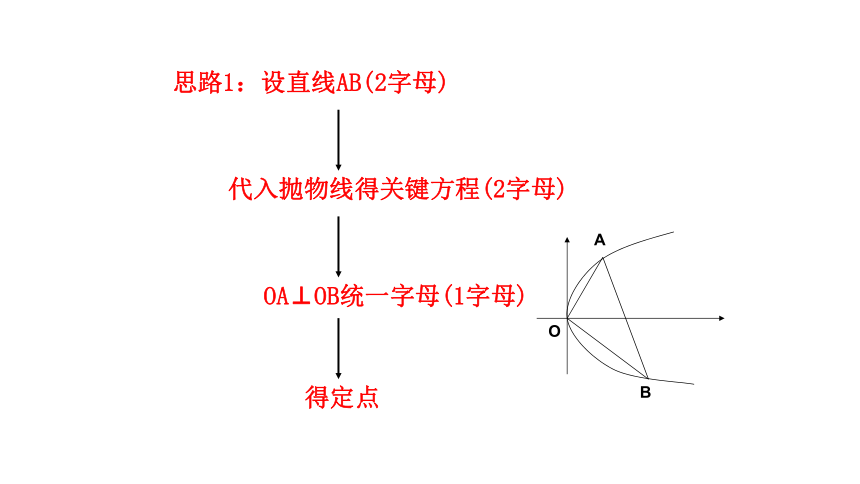
思路1:设直线AB(2字母)
O
A
B
代入抛物线得关键方程(2字母)
OA⊥OB统一字母(1字母)
得定点
O
A
B
法1:设
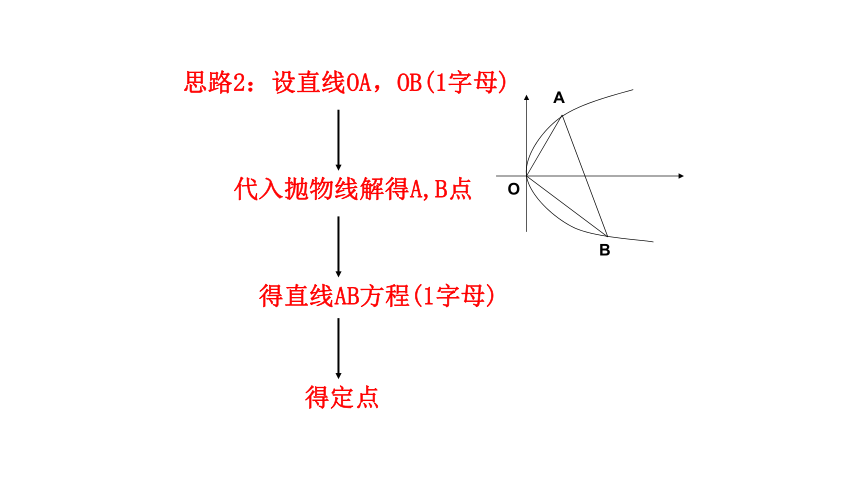
思路2:设直线OA,OB(1字母)
O
A
B
代入抛物线解得A,B点
得直线AB方程(1字母)
得定点
O
A
B
法2:
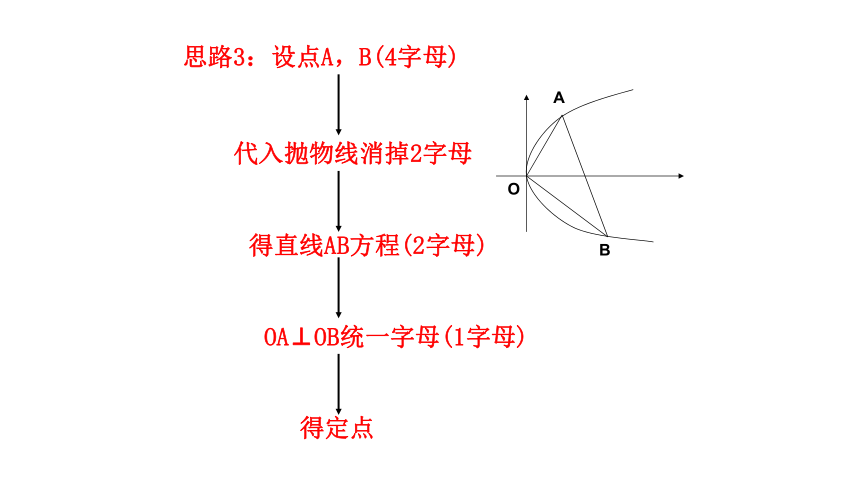
思路3:设点A,B(4字母)
O
A
B
代入抛物线消掉2字母
得直线AB方程(2字母)
得定点
OA⊥OB统一字母(1字母)
O
A
B
法3:设
规律:直线(曲线)过定点问题实质是方程与动量(变量)无关,这里的变量要合理选取,如斜率、截距、坐标等。在处理过程中,可以统一成一个变量,或统一成某个变量整体结构去解决问题。
(2)过任意一点 作两条互相垂直的弦 ,
则直线 过定点为
解析:小题猜测:极端性,当 水平时
此时 在无穷远处, ,直线
所以定点纵坐标为
O
A
B
P
当 竖直时,设为 ,
代入抛物线方程,
猜测定点为
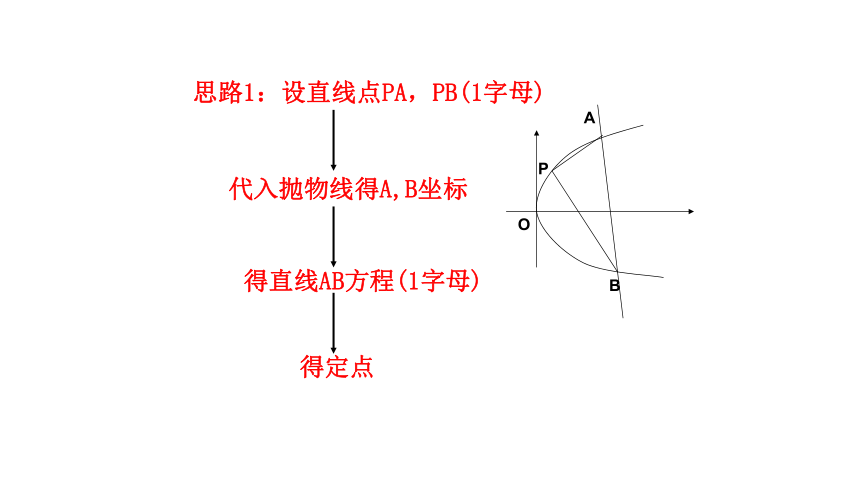
思路1:设直线点PA,PB(1字母)
代入抛物线得A,B坐标
得直线AB方程(1字母)
得定点
O
A
B
P
法1:
O
A
B
P
思路1:设点A,B(4字母)
代入抛物线消掉2字母
得直线AB方程(2字母)
得定点
PA⊥PB统一字母(1字母)
O
A
B
P
法1:
O
A
B
P
思路2:设直线AB(2字母)
代入抛物线得关键方程
k1k2=-1统一字母
代直线AB方程(1字母)
得定点
O
A
B
P
法2:
解析:小题猜测:极端性,当 水平时,
此时 ,所以定点纵坐标为
1、过原点 作抛物线 两条弦 ,
倾斜角分别为 ,
(1)若 ,则直线 过定点为
当 时, ,
所以定点为 的交点。
跟踪练习
证:设
(2)若 ,则直线 过定点为
解析: ,证明思路:注意 无意义,
则
(3)若 ,则直线 过定点为
证:设
②
①
(4)过准线上任意一点 作两条切线 ,切点为
,则直线 过定点为
解析: ,特殊化猜测。
证:设
O
A
B
P
2、已知抛物线方程为
,过点
作抛物线的两条弦
,且
斜率为
满足
,则直线
过定点 的
坐标为
O
M(1,2)
F
E
思路1:设直线ME(1字母)
代入抛物线得E点
O
M(1,2)
F
E
类比得F点
得直线EF方程(1字母)
得定点
解析:法1:
方程有一根为2,由韦达定理得另一根为
思路2:设直线EF(2字母),点M,N(4字母)
代入抛物线得关键方程
O
M(1,2)
F
E
k1k2=1统一字母
代直线EF方程(1字母)
得定点
法2:
例3、椭圆
(1)以左顶点 为直角顶点的 的顶点都在
椭圆上,则斜边 过定点
A
M
N
(二)椭圆类
思路1:特殊化取AM:y=x+2
代入椭圆得M,N坐标(1字母)
得直线AB方程(1字母)
猜测得定点坐标再证明
A
M
N
解析:
思路2:设直线MN(2字母)
代入椭圆得关键方程(2字母)
得直线AB方程(1字母)
得定点
AM⊥AN统一字母(1字母)
A
M
N
解析:
(2)设 , 为椭圆上关于 轴对称的任意
两点, 交椭圆另一点于 ,则直线 过定点
P
M
N
E
思路:设点M,N,E(4字母),直线PN方程x=my+4(1字母)
得直线ME方程(1字母)
得定点
直线PN与椭圆联立(3字母可统一成1个)
P(4,0)
M(x1,-y1)
N(x1, y1)
E(x2,y2)
N,E,P在直线PN上(3字母y1,y2,m)
解析:当M,N重合,则ME:x=0,所以定点纵坐标为0
P(4,0)
M(x1,-y1)
N(x1, y1)
E(x2,y2)
例4、
若存在一个定点 ,对于圆上任意一点 使得
为定值,则该定值为 ,定点 的
坐标为
A(-2,0)
M(x,y)
B(m, n)
思路1:设点M,B(4字母),定值 (1字母)
得定值,定点
x,y系数,常数为0
代入等式恒成立
A(-2,0)
M(x,y)
B(m, n)
解析1:设B(m,n),M(x,y),
对圆上任意点M(x,y)恒成立
思路2:取M特殊点,猜测出B点位置
证明定点对任意M恒成立
A(-2,0)
M(x,y)
B(m, n)
解析2:不妨取M1(0,1),M2(0,-1)
又取M3(-1,0),M4(1,0)
例5、椭圆 ,过 作直线l交椭圆于
,若存在一个定点 ,使得
恒成立,则点 坐标为
解析:当l水平时,则|BN|=|BM|,所以B只可能在y
轴上,设B(0,t)
当l竖直时,则 ,则BA为角MBN的角
平分线
取
下证对任意直线l 都适合
例6、椭圆 的左右顶点分别为 ,
分别交椭圆于
其中 ,则直线 过定点
解析:直线TMA:
直线TBN:
分别与椭圆方程联立,同
时考虑到
T(9,m)
M
N
B
A
D
O
法1:当 时,直线MN:
令 解得
当 时,直线MN:
所以直线MN必过定点(1,0)
当 时,
法2:当 时,直线MN: ,过D(1,0)点
所以直线MN必过定点(1,0)
例7、椭圆 的,过右焦点 作与坐标轴不垂
直的直线 交椭圆于 ,设点 是点 关于 轴的
对称点,求一定点 ,使得 三点共线,
则点 的坐标为
A(x1,y1)
C(x1,-y1)
F(2,0)
O
N
B(x2,t2)
解析:根据对称性,知N必在x轴上,设N(t,0)
斜率分别为 且
1、已知椭圆
,过点
作椭圆的两条弦
,又两弦的中点
分别为
求证:直线 过定点,并求出定点坐标。
答案:
跟踪练习
解析:
2、已知点A(-1,0),B(1,-1)和抛物线C:y2=4x,
O为坐标原点,过点A的动直线l交抛物线C于M、P,
直线MB交抛物线C于另一点Q.
(1)证明: 为定值;
(2)若△POM的面积为 ,求向量 与 的夹角;
(3)证明直线PQ恒过一个定点。
答案:
解析(1)
(2)
(3)
由(1)
3、已知椭圆 上下顶点分别为
设直线 斜率分别为
在椭圆上且异于
与直线
分别交于
(1)
求证: 为定值;
(2)当 运动时,以 为直径的圆是否过定点?
并证明。
答案:
解析(1)
(2)
三、定值问题
例题分析
例1、抛物线 ,动直线 过点
,交抛物线于 ,且原点为 中点
求证: 为定值。
O
A
B
N
M(a,0)
l
解析:小题猜测:特殊化,当
竖直时,显然
证:设
分子
注意:此题可以有多种问法,如
例2、不为原点的点 在抛物线
上,过P作斜率相反的两条弦PE,PF。
求证:EF斜率为定值。
O
P
E
F
解析:猜测:极端化,当E,F重合时,EF为切线,所以
定值为P关于x轴对称点处的切线斜率。即为P处切线斜
率的相反数
推广:椭圆,双曲线,圆都有类似性质。
证法1:
O
P
E
F
类比得到
所以
证法2:
O
P
E
F
例3、A为抛物线 上一动点,B(4,0),是否存在
垂直于x轴的定直线l被AB为直径的圆截得的弦长为定
值?有则求出定直线和定值,无则说明理由。
O
A
B
C
D
E
F
L:x=m
解析:假设存在满足条件的直线l:x=m
例4、已知椭圆中心在原点,焦点在x轴上,斜率为1
的直线过右焦点交椭圆于A,B, 与
共线。
(1)求椭圆离心率e;
(2)设M为椭圆上任意一点,且
求证: 为定值。
解析(1)
解析(2)探寻定值,特殊化,若M=A,则
证:
例5、过椭圆 右焦点F的弦AB
求证: 为定值;
F
O
A
B
解析:特殊化易得定值
法1:普通方程
法2:直线参数方程
法3:椭圆极坐标方程
例6、过椭圆 右焦点F的弦AB
在x轴上是否存在一个定点M(a,0),使得
为定值,有则求出,无则说明理由。
解析:
F
O
A
B
M(t,0)
跟踪练习
1、椭圆 ,过 作斜率相反的两条弦
求证:EF斜率为定值。
P
E
F
答案:
解析:略
2、动圆过点P(2,0),且M在抛物线 上,
圆M被y轴截得的弦长|AB|为定值,求出该定值和抛
物线方程。
答案:
解析:设M(a,b)
O
M(a,b)
P(2,0)
B
A
3、椭圆 ,过 的直线l与椭圆交于
A,B,与直线x=-4交于E,
求证: 为定值。
Q
O
A
B
E
l
答案:0
解析:
Q
O
A
B
E
l
4、椭圆 中心 , 在椭圆上
求证:(1) 为定值;
(2) 为定值。
d
O
A
B
答案:(1)
解析(1)设普通坐标运算复杂,考虑极坐标
解析(2)
d
O
A
B
四、定直线问题
例题分析
例1、椭圆 左右顶点分别为A,B,直线
与椭圆交于P,Q,AP与BQ交于S。
求证: 变化时,求证S在一定直线 上。
P
O
A
B
Q
S
解析:法1:
P(x1,y1)
O
A(-2,0)
B(2,0)
Q(x2,y2)
S
P(x1,y1)
O
A(-2,0)
B(2,0)
Q(x2,y2)
S
法2:前面同法1,
规律:先猜测,再证明减轻难度。
跟踪练习
1、椭圆 过P(4,1)的动直线l与椭圆交于
A,B,点Q在线段AB上,满足
求证:点Q在一定直线上。
A(x1,y1)
O
Q
B(x2,y2)
P(4,1)
解析:
答案:
A(x1,y1)
O
Q
B(x2,y2)
P(4,1)
规律:乘积变比例,比例引参数,向量化坐标。
五、其他定量问题
例题分析
例1、双曲线 ,直线l是圆
上动点P处的切线,l与双曲线交于两点A,B
求证: 大小为定值。
解析:特殊化取 ,易得
解析:
例2、椭圆 , 为原点
(1)动点 满足: ,其中
M,N在椭圆上,且
求证: 为定值;
(2)若过动点 的椭圆两切线斜率之积为
定值m,试探究m的取值范围并确定点P的轨迹图形。
解析(1)
解析(2)
跟踪练习
1、椭圆 ,四边形ABCD的顶点都在椭圆
上,且对角线AC,BD过原点O,若
(1)求 的最值;
(2)求证:四边形ABCD的面积为定值。
(2)
答案:(1)
解析(1)
解析(2)
规律:
解析几何中的定量问题
2023届高考数学复习专题 ★★
一、定量问题的思想方法
思想方法:定量问题包括定点,定值,定角,定直线,
定面积等等。小题可以特殊化、极端化猜测得出,大
题则一般可以先猜再证。
能力要求:
(1)会猜——特殊化,极端化
(2)会证——
①设方程(直线通常为y=kx+b或x=my+n)
②联立方程组得关键方程
③转化几何条件建立代数关系
④利用韦达定理建立等式,统一参数字母
⑤求出定量
二、定点问题
例1、抛物线
(1)过原点 作两条互相垂直的弦 ,则直线
过定点为
O
A
B
解析:小题猜测:根据对称性,定点肯定在x轴上,
再取 ,易得
猜测定点
证:证明方法很多,这里略举几种,
后面的例题通法为主。
(一)抛物线类
思路1:设直线AB(2字母)
O
A
B
代入抛物线得关键方程(2字母)
OA⊥OB统一字母(1字母)
得定点
O
A
B
法1:设
思路2:设直线OA,OB(1字母)
O
A
B
代入抛物线解得A,B点
得直线AB方程(1字母)
得定点
O
A
B
法2:
思路3:设点A,B(4字母)
O
A
B
代入抛物线消掉2字母
得直线AB方程(2字母)
得定点
OA⊥OB统一字母(1字母)
O
A
B
法3:设
规律:直线(曲线)过定点问题实质是方程与动量(变量)无关,这里的变量要合理选取,如斜率、截距、坐标等。在处理过程中,可以统一成一个变量,或统一成某个变量整体结构去解决问题。
(2)过任意一点 作两条互相垂直的弦 ,
则直线 过定点为
解析:小题猜测:极端性,当 水平时
此时 在无穷远处, ,直线
所以定点纵坐标为
O
A
B
P
当 竖直时,设为 ,
代入抛物线方程,
猜测定点为
思路1:设直线点PA,PB(1字母)
代入抛物线得A,B坐标
得直线AB方程(1字母)
得定点
O
A
B
P
法1:
O
A
B
P
思路1:设点A,B(4字母)
代入抛物线消掉2字母
得直线AB方程(2字母)
得定点
PA⊥PB统一字母(1字母)
O
A
B
P
法1:
O
A
B
P
思路2:设直线AB(2字母)
代入抛物线得关键方程
k1k2=-1统一字母
代直线AB方程(1字母)
得定点
O
A
B
P
法2:
解析:小题猜测:极端性,当 水平时,
此时 ,所以定点纵坐标为
1、过原点 作抛物线 两条弦 ,
倾斜角分别为 ,
(1)若 ,则直线 过定点为
当 时, ,
所以定点为 的交点。
跟踪练习
证:设
(2)若 ,则直线 过定点为
解析: ,证明思路:注意 无意义,
则
(3)若 ,则直线 过定点为
证:设
②
①
(4)过准线上任意一点 作两条切线 ,切点为
,则直线 过定点为
解析: ,特殊化猜测。
证:设
O
A
B
P
2、已知抛物线方程为
,过点
作抛物线的两条弦
,且
斜率为
满足
,则直线
过定点 的
坐标为
O
M(1,2)
F
E
思路1:设直线ME(1字母)
代入抛物线得E点
O
M(1,2)
F
E
类比得F点
得直线EF方程(1字母)
得定点
解析:法1:
方程有一根为2,由韦达定理得另一根为
思路2:设直线EF(2字母),点M,N(4字母)
代入抛物线得关键方程
O
M(1,2)
F
E
k1k2=1统一字母
代直线EF方程(1字母)
得定点
法2:
例3、椭圆
(1)以左顶点 为直角顶点的 的顶点都在
椭圆上,则斜边 过定点
A
M
N
(二)椭圆类
思路1:特殊化取AM:y=x+2
代入椭圆得M,N坐标(1字母)
得直线AB方程(1字母)
猜测得定点坐标再证明
A
M
N
解析:
思路2:设直线MN(2字母)
代入椭圆得关键方程(2字母)
得直线AB方程(1字母)
得定点
AM⊥AN统一字母(1字母)
A
M
N
解析:
(2)设 , 为椭圆上关于 轴对称的任意
两点, 交椭圆另一点于 ,则直线 过定点
P
M
N
E
思路:设点M,N,E(4字母),直线PN方程x=my+4(1字母)
得直线ME方程(1字母)
得定点
直线PN与椭圆联立(3字母可统一成1个)
P(4,0)
M(x1,-y1)
N(x1, y1)
E(x2,y2)
N,E,P在直线PN上(3字母y1,y2,m)
解析:当M,N重合,则ME:x=0,所以定点纵坐标为0
P(4,0)
M(x1,-y1)
N(x1, y1)
E(x2,y2)
例4、
若存在一个定点 ,对于圆上任意一点 使得
为定值,则该定值为 ,定点 的
坐标为
A(-2,0)
M(x,y)
B(m, n)
思路1:设点M,B(4字母),定值 (1字母)
得定值,定点
x,y系数,常数为0
代入等式恒成立
A(-2,0)
M(x,y)
B(m, n)
解析1:设B(m,n),M(x,y),
对圆上任意点M(x,y)恒成立
思路2:取M特殊点,猜测出B点位置
证明定点对任意M恒成立
A(-2,0)
M(x,y)
B(m, n)
解析2:不妨取M1(0,1),M2(0,-1)
又取M3(-1,0),M4(1,0)
例5、椭圆 ,过 作直线l交椭圆于
,若存在一个定点 ,使得
恒成立,则点 坐标为
解析:当l水平时,则|BN|=|BM|,所以B只可能在y
轴上,设B(0,t)
当l竖直时,则 ,则BA为角MBN的角
平分线
取
下证对任意直线l 都适合
例6、椭圆 的左右顶点分别为 ,
分别交椭圆于
其中 ,则直线 过定点
解析:直线TMA:
直线TBN:
分别与椭圆方程联立,同
时考虑到
T(9,m)
M
N
B
A
D
O
法1:当 时,直线MN:
令 解得
当 时,直线MN:
所以直线MN必过定点(1,0)
当 时,
法2:当 时,直线MN: ,过D(1,0)点
所以直线MN必过定点(1,0)
例7、椭圆 的,过右焦点 作与坐标轴不垂
直的直线 交椭圆于 ,设点 是点 关于 轴的
对称点,求一定点 ,使得 三点共线,
则点 的坐标为
A(x1,y1)
C(x1,-y1)
F(2,0)
O
N
B(x2,t2)
解析:根据对称性,知N必在x轴上,设N(t,0)
斜率分别为 且
1、已知椭圆
,过点
作椭圆的两条弦
,又两弦的中点
分别为
求证:直线 过定点,并求出定点坐标。
答案:
跟踪练习
解析:
2、已知点A(-1,0),B(1,-1)和抛物线C:y2=4x,
O为坐标原点,过点A的动直线l交抛物线C于M、P,
直线MB交抛物线C于另一点Q.
(1)证明: 为定值;
(2)若△POM的面积为 ,求向量 与 的夹角;
(3)证明直线PQ恒过一个定点。
答案:
解析(1)
(2)
(3)
由(1)
3、已知椭圆 上下顶点分别为
设直线 斜率分别为
在椭圆上且异于
与直线
分别交于
(1)
求证: 为定值;
(2)当 运动时,以 为直径的圆是否过定点?
并证明。
答案:
解析(1)
(2)
三、定值问题
例题分析
例1、抛物线 ,动直线 过点
,交抛物线于 ,且原点为 中点
求证: 为定值。
O
A
B
N
M(a,0)
l
解析:小题猜测:特殊化,当
竖直时,显然
证:设
分子
注意:此题可以有多种问法,如
例2、不为原点的点 在抛物线
上,过P作斜率相反的两条弦PE,PF。
求证:EF斜率为定值。
O
P
E
F
解析:猜测:极端化,当E,F重合时,EF为切线,所以
定值为P关于x轴对称点处的切线斜率。即为P处切线斜
率的相反数
推广:椭圆,双曲线,圆都有类似性质。
证法1:
O
P
E
F
类比得到
所以
证法2:
O
P
E
F
例3、A为抛物线 上一动点,B(4,0),是否存在
垂直于x轴的定直线l被AB为直径的圆截得的弦长为定
值?有则求出定直线和定值,无则说明理由。
O
A
B
C
D
E
F
L:x=m
解析:假设存在满足条件的直线l:x=m
例4、已知椭圆中心在原点,焦点在x轴上,斜率为1
的直线过右焦点交椭圆于A,B, 与
共线。
(1)求椭圆离心率e;
(2)设M为椭圆上任意一点,且
求证: 为定值。
解析(1)
解析(2)探寻定值,特殊化,若M=A,则
证:
例5、过椭圆 右焦点F的弦AB
求证: 为定值;
F
O
A
B
解析:特殊化易得定值
法1:普通方程
法2:直线参数方程
法3:椭圆极坐标方程
例6、过椭圆 右焦点F的弦AB
在x轴上是否存在一个定点M(a,0),使得
为定值,有则求出,无则说明理由。
解析:
F
O
A
B
M(t,0)
跟踪练习
1、椭圆 ,过 作斜率相反的两条弦
求证:EF斜率为定值。
P
E
F
答案:
解析:略
2、动圆过点P(2,0),且M在抛物线 上,
圆M被y轴截得的弦长|AB|为定值,求出该定值和抛
物线方程。
答案:
解析:设M(a,b)
O
M(a,b)
P(2,0)
B
A
3、椭圆 ,过 的直线l与椭圆交于
A,B,与直线x=-4交于E,
求证: 为定值。
Q
O
A
B
E
l
答案:0
解析:
Q
O
A
B
E
l
4、椭圆 中心 , 在椭圆上
求证:(1) 为定值;
(2) 为定值。
d
O
A
B
答案:(1)
解析(1)设普通坐标运算复杂,考虑极坐标
解析(2)
d
O
A
B
四、定直线问题
例题分析
例1、椭圆 左右顶点分别为A,B,直线
与椭圆交于P,Q,AP与BQ交于S。
求证: 变化时,求证S在一定直线 上。
P
O
A
B
Q
S
解析:法1:
P(x1,y1)
O
A(-2,0)
B(2,0)
Q(x2,y2)
S
P(x1,y1)
O
A(-2,0)
B(2,0)
Q(x2,y2)
S
法2:前面同法1,
规律:先猜测,再证明减轻难度。
跟踪练习
1、椭圆 过P(4,1)的动直线l与椭圆交于
A,B,点Q在线段AB上,满足
求证:点Q在一定直线上。
A(x1,y1)
O
Q
B(x2,y2)
P(4,1)
解析:
答案:
A(x1,y1)
O
Q
B(x2,y2)
P(4,1)
规律:乘积变比例,比例引参数,向量化坐标。
五、其他定量问题
例题分析
例1、双曲线 ,直线l是圆
上动点P处的切线,l与双曲线交于两点A,B
求证: 大小为定值。
解析:特殊化取 ,易得
解析:
例2、椭圆 , 为原点
(1)动点 满足: ,其中
M,N在椭圆上,且
求证: 为定值;
(2)若过动点 的椭圆两切线斜率之积为
定值m,试探究m的取值范围并确定点P的轨迹图形。
解析(1)
解析(2)
跟踪练习
1、椭圆 ,四边形ABCD的顶点都在椭圆
上,且对角线AC,BD过原点O,若
(1)求 的最值;
(2)求证:四边形ABCD的面积为定值。
(2)
答案:(1)
解析(1)
解析(2)
规律:
同课章节目录
