2023届高考数学复习专题 ★★洛必达法则 课件(共39张PPT)
文档属性
| 名称 | 2023届高考数学复习专题 ★★洛必达法则 课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 09:58:38 | ||
图片预览










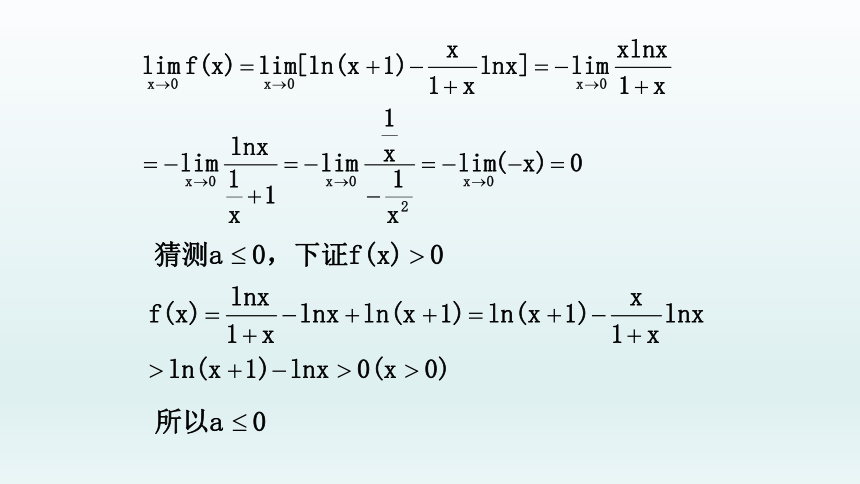
文档简介
(共39张PPT)
2023届高考数学复习专题 ★★
洛必达法则
一、洛必达法则
2、结构:高中主要用于 , 两种类型
其他结构需转化才能应用。
1、功能:用于求极限值。
解读洛必达法则:
洛必达:1661-1704
法国数学家
3、注意事项:未定式可以连续应用,
已定式不能再用。
二、洛必达法则求极限
例1.求
解析: 型
二、洛必达法则求极限
例2.求
解析:不适合条件,需转化
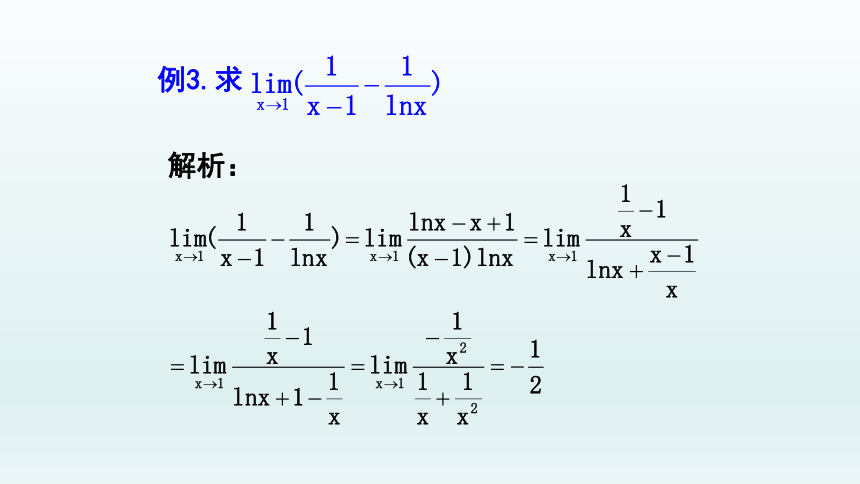
例3.求
解析:
例4.求
解析:
注意: 为已定式,不能再用洛必达法则。
例5.若 ,求
解析:
三、洛必达法则的应用
1.不等式恒成立或能成立题目。
适用题型:
2.能分离参数成 或 ,归结
为求 的某个最值(或其极限值)问题。
3.常规方法不易求得最值或其极限值(往往
多次求导后仍为超越结构)。
4.在某个端点或断点处应用洛必达法则猜测
出最值(或极限值)后需要证明。
的解集为 ,若存在,求出
(2)是否存在实数 ,使得关于 的不等式
(1)求
例题选讲
的单调区间和极值;
的范围;不存在,说明理由。
解析:(1)略。
(2)分析:注意定义域 ,题目等价于
说明:对 和 哪个端点求极限?
法1、两个都求取小;
法2、取特殊值比较取舍。
例2.(08全国理2)
(1)求f(x)单调区间;
(2)若对 都有 ,求a范围。
解析:(1)略
(2)
当 时,
当 时,
为必要条件
下证
因为
所以
所以
证(1):不等式证明结构较复杂时可以考虑变形后证明。
构造函数
求导,判断单调性解决(略)
(2)恒(能)不等式两种思路:
不分离参数函数法分析(要讨论参数);
分离参数考虑最值(必要时用洛必达法则)。
这里主要提供第二种思路。
①若
,则
在 必能小于0,
所以不等式不可能恒成立(舍)
②若
,若
,恒成立
若
,则
注意
用导数法判断单调性难以解决,所以猜测最小
极限值点在0或
下面求
,
的最小值或最小极限值。
位置,
由洛必达法则:
为必要条件。
下证
因为
,
所以
在
增
所以
在
增
所以
解析:(1)
(2)即
,
恒成立
所以猜测
下证
当 时,
因为
所以
在
增,所以
所以
在
减,所以
所以
同理可证
时
所以
例5.复旦周考3(21):已知函数
(1)当
时,求
的最小值;
时,
恒成立,求实数
的取值范围。
(2)若
解析:(1)
(2) 法1:
对 恒成立
时,
①
②
时,
恒成立
猜测 下证:
即需证
令
因为
所以
增,所以
得证。
所以
法2:令 即,
对
恒成立
令
轴
,
,
g(t)
t0
1
3
①若
时,
则
在
必有唯一零点
所以
在
减,
增
,所以
不适合。
②若
时,
在
增,因为
,显然适合
所以
法3:
对
恒成立,即
考虑函数
,
(都过定点(1,2))
所以
在
减,
增
3
2
(1,2)
1
因为
,所以
在
为凹函数
所以
例6.
巴蜀周考6(22):已知函数
(1)当
时,求函数
在
上的最小值;
在
上恒成立,求实数
的取值范围。
(2)若
(2)法1:
对
恒成立
又
所以
所以
在
减
解析:(1)
即 对 恒成立
法2:
即
对
上恒成立
注意
①若
,则
在
减,所以
适合
②若
,令
所以
在
减,
增。
1)若
时,则
在
增,
,则在该区间
不适合;
2)若
时,则
在
减,所以
适合。
综上:
法3:即
,考虑函数
(都过点(0,m))
①当
时,
在
减,
在
增,适合;
m
m
②
当
时,适合;
时,
在
增。
③当
此时需
综上:
1.(2010全国新课标)
(1)a=0时,求f(x)单调区间;
(2)若 时都有 ,求a范围。
跟踪练习
2.关于x的不等式 在
有解,求实数a的取值范围。
3.(2011武汉调研)
时,不等式
恒成立,求实数a的取值范围。
2023届高考数学复习专题 ★★
洛必达法则
一、洛必达法则
2、结构:高中主要用于 , 两种类型
其他结构需转化才能应用。
1、功能:用于求极限值。
解读洛必达法则:
洛必达:1661-1704
法国数学家
3、注意事项:未定式可以连续应用,
已定式不能再用。
二、洛必达法则求极限
例1.求
解析: 型
二、洛必达法则求极限
例2.求
解析:不适合条件,需转化
例3.求
解析:
例4.求
解析:
注意: 为已定式,不能再用洛必达法则。
例5.若 ,求
解析:
三、洛必达法则的应用
1.不等式恒成立或能成立题目。
适用题型:
2.能分离参数成 或 ,归结
为求 的某个最值(或其极限值)问题。
3.常规方法不易求得最值或其极限值(往往
多次求导后仍为超越结构)。
4.在某个端点或断点处应用洛必达法则猜测
出最值(或极限值)后需要证明。
的解集为 ,若存在,求出
(2)是否存在实数 ,使得关于 的不等式
(1)求
例题选讲
的单调区间和极值;
的范围;不存在,说明理由。
解析:(1)略。
(2)分析:注意定义域 ,题目等价于
说明:对 和 哪个端点求极限?
法1、两个都求取小;
法2、取特殊值比较取舍。
例2.(08全国理2)
(1)求f(x)单调区间;
(2)若对 都有 ,求a范围。
解析:(1)略
(2)
当 时,
当 时,
为必要条件
下证
因为
所以
所以
证(1):不等式证明结构较复杂时可以考虑变形后证明。
构造函数
求导,判断单调性解决(略)
(2)恒(能)不等式两种思路:
不分离参数函数法分析(要讨论参数);
分离参数考虑最值(必要时用洛必达法则)。
这里主要提供第二种思路。
①若
,则
在 必能小于0,
所以不等式不可能恒成立(舍)
②若
,若
,恒成立
若
,则
注意
用导数法判断单调性难以解决,所以猜测最小
极限值点在0或
下面求
,
的最小值或最小极限值。
位置,
由洛必达法则:
为必要条件。
下证
因为
,
所以
在
增
所以
在
增
所以
解析:(1)
(2)即
,
恒成立
所以猜测
下证
当 时,
因为
所以
在
增,所以
所以
在
减,所以
所以
同理可证
时
所以
例5.复旦周考3(21):已知函数
(1)当
时,求
的最小值;
时,
恒成立,求实数
的取值范围。
(2)若
解析:(1)
(2) 法1:
对 恒成立
时,
①
②
时,
恒成立
猜测 下证:
即需证
令
因为
所以
增,所以
得证。
所以
法2:令 即,
对
恒成立
令
轴
,
,
g(t)
t0
1
3
①若
时,
则
在
必有唯一零点
所以
在
减,
增
,所以
不适合。
②若
时,
在
增,因为
,显然适合
所以
法3:
对
恒成立,即
考虑函数
,
(都过定点(1,2))
所以
在
减,
增
3
2
(1,2)
1
因为
,所以
在
为凹函数
所以
例6.
巴蜀周考6(22):已知函数
(1)当
时,求函数
在
上的最小值;
在
上恒成立,求实数
的取值范围。
(2)若
(2)法1:
对
恒成立
又
所以
所以
在
减
解析:(1)
即 对 恒成立
法2:
即
对
上恒成立
注意
①若
,则
在
减,所以
适合
②若
,令
所以
在
减,
增。
1)若
时,则
在
增,
,则在该区间
不适合;
2)若
时,则
在
减,所以
适合。
综上:
法3:即
,考虑函数
(都过点(0,m))
①当
时,
在
减,
在
增,适合;
m
m
②
当
时,适合;
时,
在
增。
③当
此时需
综上:
1.(2010全国新课标)
(1)a=0时,求f(x)单调区间;
(2)若 时都有 ,求a范围。
跟踪练习
2.关于x的不等式 在
有解,求实数a的取值范围。
3.(2011武汉调研)
时,不等式
恒成立,求实数a的取值范围。
同课章节目录
