2023届高考数学复习专题 ★★圆锥曲线范围、最值问题 课件(共59张PPT)
文档属性
| 名称 | 2023届高考数学复习专题 ★★圆锥曲线范围、最值问题 课件(共59张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 712.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 09:59:01 | ||
图片预览





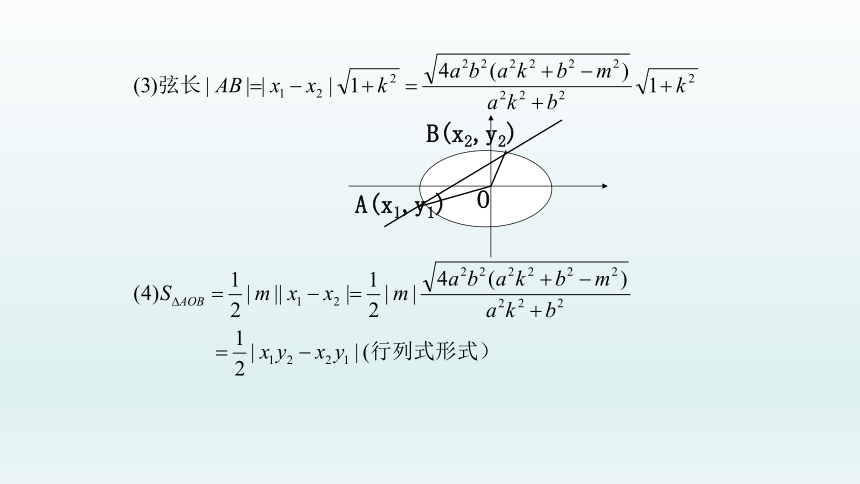

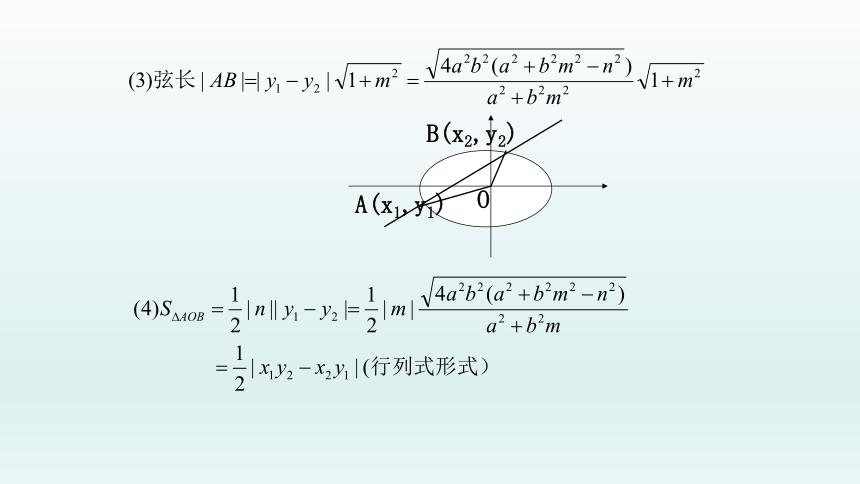
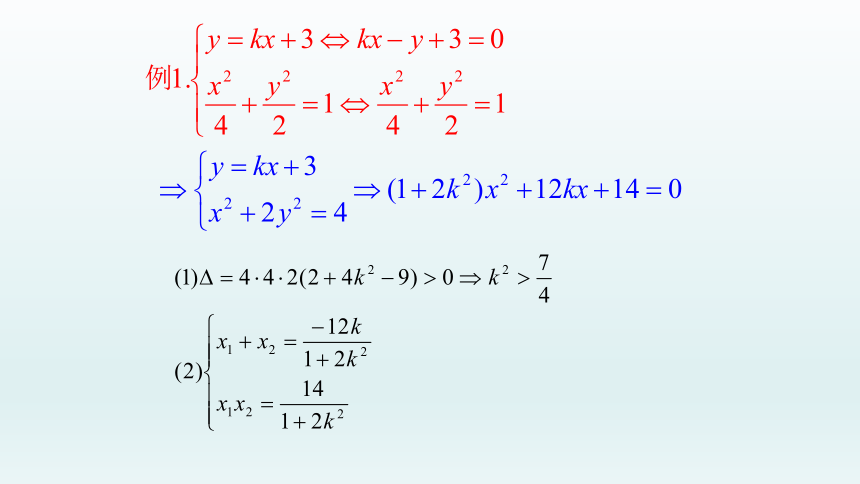
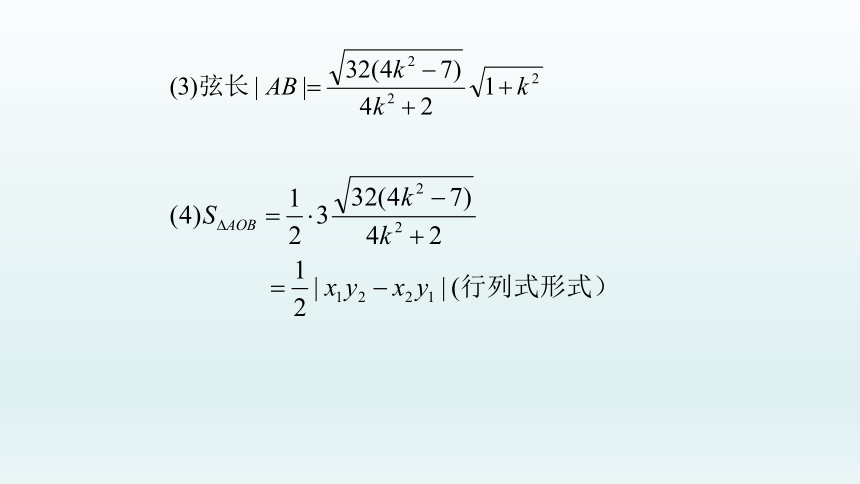

文档简介
(共59张PPT)
圆锥曲线中的最值范围问题
2023届高考数学复习专题 ★★
一、知识储备
1、点的坐标
x
y
O
点无明显的几何条件
在o为圆心的圆上
在(a,b)为圆心的圆上
在椭圆上
在极坐标系内
2、直线方程的选取
不包括竖直,过定点(0,m)
不包括水平,过定点(n,0)
为倾斜角,
t表示有向线段PQ的数量。
P(a,b)为直线上的定点,
Q(x,y)为直线上的动点。
x
y
O
(0,m)
(n,0)
3、曲线方程的选取
(这里主要指椭圆)
(1)纵截式中的常见结论
4、关键方程的处理
A(x1,y1)
B(x2,y2)
O
(2)横截式中的常见结论
A(x1,y1)
B(x2,y2)
O
解析几何问题分两类:定量和变量问题,所谓变量
问题即范围和最值问题。两类问题都常常要将几何
条件合理转化为代数形式再进行运算。通常的转化
手段有两种:代点法如点差、点积法等,更常用的
是转化到直线和曲线的交点坐标整体应用韦达定理
进行运算,涉及到范围问题要考虑判别式范围。而
将几何条件代数化是学生的难点,下面将常见的转
化手段归类并举例说明。
二、几何条件代数转化
类型一、弦长
A(x1,y1)
B(x2,y2)
O
A(0,b)
O
B
C
A(0,b)
O
B
C
A
O
B
P(1,0)
类型二、三角形AOB面积
O
O
O
规律:若为如图四边形,则为平行四边形,转化求得。
O
O
类型三、三角形AFB面积的几种表示
O
F
规律:1、三角形AFB面积用横分割或极坐标较好;
2、若延长AF,BF交椭圆于C,D,四边形的面积则
用极坐标好。
O
类型四、AB上的分点问题
O
P
规律:注意长度比和向量系数的符号关系:
P为外分点:
P为内分点:
O
P
O
M
类型五、以AB为直径的圆过定点
O
类型六、A,B在 为圆心的同一圆上
O
类型七、存在A,B关于直线l对称
O
l
类型八、PA,PB的对称轴水平或竖直
O
O
l
O
l:y=2x+b
O
l
类型九、PA,PB为切线
O
O
A
B
P
类型十、离心率范围
O
与离心率有关的结论:
O
例1. F为圆锥曲线的左焦点,直线l过点F且倾斜角
为60°直线l与椭圆交于A,B两点,且|AF|=t|BF|
(1)若t=2,求e,并判断曲线类型;
(2)若曲线为双曲线,求t范围。
例2.椭圆
与圆
有四个不同交点,求离心率
的范围。
例3.椭圆 上存在一点P,使得
,求离心率
的范围。
O
O
O
练习1.双曲线
,直线
与双曲线左右两支有一个交点时,求离心率范围。
练习2.双曲线 ,F1(-c,0), F2(c,0)为两焦点,若双曲线上存在一个点P,使 成立,求e范围。
O
圆锥曲线中的最值范围问题
2023届高考数学复习专题 ★★
一、知识储备
1、点的坐标
x
y
O
点无明显的几何条件
在o为圆心的圆上
在(a,b)为圆心的圆上
在椭圆上
在极坐标系内
2、直线方程的选取
不包括竖直,过定点(0,m)
不包括水平,过定点(n,0)
为倾斜角,
t表示有向线段PQ的数量。
P(a,b)为直线上的定点,
Q(x,y)为直线上的动点。
x
y
O
(0,m)
(n,0)
3、曲线方程的选取
(这里主要指椭圆)
(1)纵截式中的常见结论
4、关键方程的处理
A(x1,y1)
B(x2,y2)
O
(2)横截式中的常见结论
A(x1,y1)
B(x2,y2)
O
解析几何问题分两类:定量和变量问题,所谓变量
问题即范围和最值问题。两类问题都常常要将几何
条件合理转化为代数形式再进行运算。通常的转化
手段有两种:代点法如点差、点积法等,更常用的
是转化到直线和曲线的交点坐标整体应用韦达定理
进行运算,涉及到范围问题要考虑判别式范围。而
将几何条件代数化是学生的难点,下面将常见的转
化手段归类并举例说明。
二、几何条件代数转化
类型一、弦长
A(x1,y1)
B(x2,y2)
O
A(0,b)
O
B
C
A(0,b)
O
B
C
A
O
B
P(1,0)
类型二、三角形AOB面积
O
O
O
规律:若为如图四边形,则为平行四边形,转化求得。
O
O
类型三、三角形AFB面积的几种表示
O
F
规律:1、三角形AFB面积用横分割或极坐标较好;
2、若延长AF,BF交椭圆于C,D,四边形的面积则
用极坐标好。
O
类型四、AB上的分点问题
O
P
规律:注意长度比和向量系数的符号关系:
P为外分点:
P为内分点:
O
P
O
M
类型五、以AB为直径的圆过定点
O
类型六、A,B在 为圆心的同一圆上
O
类型七、存在A,B关于直线l对称
O
l
类型八、PA,PB的对称轴水平或竖直
O
O
l
O
l:y=2x+b
O
l
类型九、PA,PB为切线
O
O
A
B
P
类型十、离心率范围
O
与离心率有关的结论:
O
例1. F为圆锥曲线的左焦点,直线l过点F且倾斜角
为60°直线l与椭圆交于A,B两点,且|AF|=t|BF|
(1)若t=2,求e,并判断曲线类型;
(2)若曲线为双曲线,求t范围。
例2.椭圆
与圆
有四个不同交点,求离心率
的范围。
例3.椭圆 上存在一点P,使得
,求离心率
的范围。
O
O
O
练习1.双曲线
,直线
与双曲线左右两支有一个交点时,求离心率范围。
练习2.双曲线 ,F1(-c,0), F2(c,0)为两焦点,若双曲线上存在一个点P,使 成立,求e范围。
O
同课章节目录
