2022-2023学年人教版九年级下册数学 第二十八章 锐角三角函数 单元检测(无答案)
文档属性
| 名称 | 2022-2023学年人教版九年级下册数学 第二十八章 锐角三角函数 单元检测(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 11:15:32 | ||
图片预览


文档简介
2022-2023年人教版九年级下学期数学
第二十八章 锐角三角函数 单元检测
一、单选题(每题3分,共18分)
1.在△ABC中,∠C=90°,sinB=,b=,则a等于( )
A. B.1 C.2 D.3
2.如图,在Rt△ABC中,,,,将△ABC绕点A逆时针旋转得到,使点落在AB边上,连结,则的值为( )
A. B. C. D.
3.如图,等腰中,交于点D,则的值为( )
A. B. C.3 D.
4.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35° B.mcos35° C. D.
5.如图,在中,,且.若,,则的长度为( )
A. B. C. D.8
6.如图,在中,,,,则的值为( )
A. B. C. D.
7.如图,在中,,则的值为( )
A. B. C. D.
8.如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则BD的值( )
A.2 B. C. D.5
9.如图,网格中小正方形的边长均为1,△ABC的顶点都在格点上,则cos∠BAC等于( )
A. B. C. D.
10.在中,、均为锐角,且,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
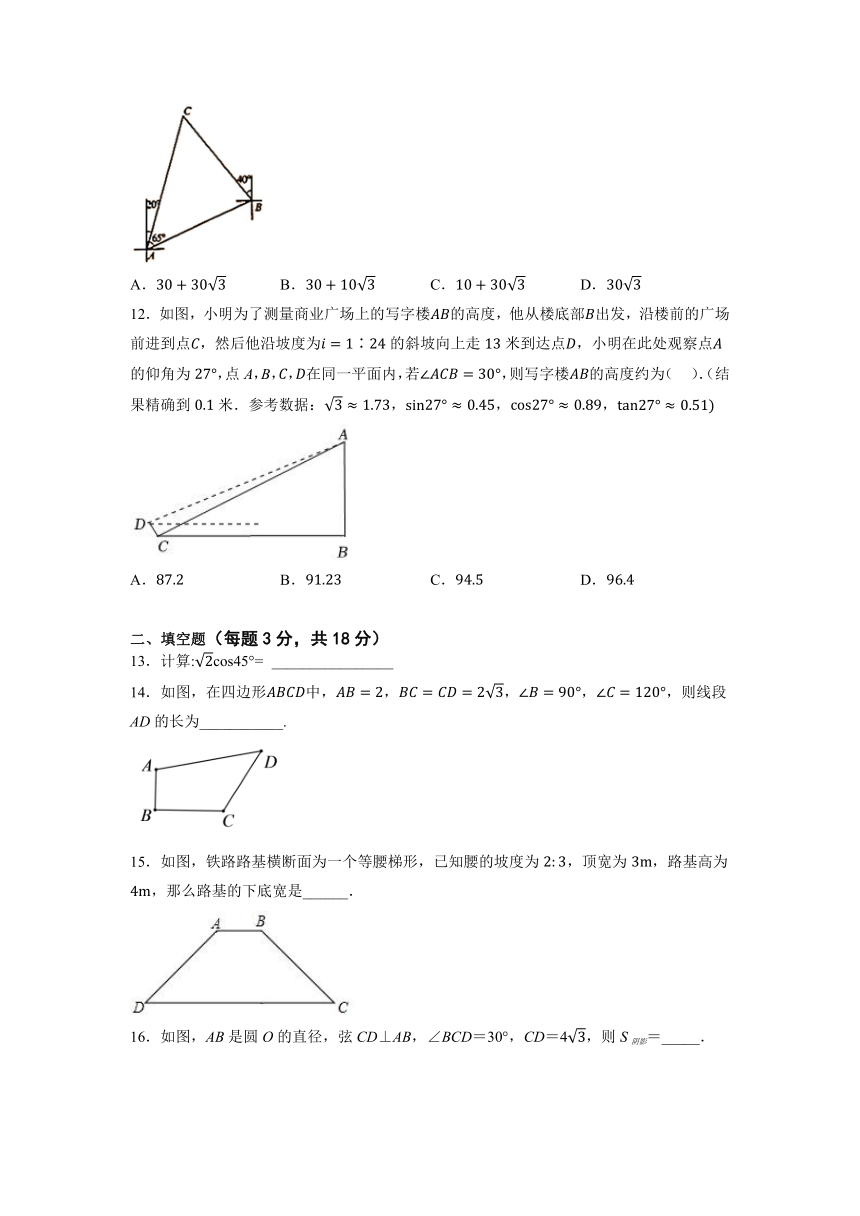
11.如图,一艘船由港沿北偏东65°方向航行至港,然后再沿北偏西40°方向航行至港,港在港北偏东20°方向,则,两港之间的距离为( ).
A. B. C. D.
12.如图,小明为了测量商业广场上的写字楼的高度,他从楼底部出发,沿楼前的广场前进到点,然后他沿坡度为∶的斜坡向上走米到达点,小明在此处观察点的仰角为,点A,B,,在同一平面内,若,则写字楼的高度约为( ).(结果精确到米.参考数据:,,,
A. B. C. D.
二、填空题(每题3分,共18分)
13.计算:cos45°= ________________
14.如图,在四边形中,,,,,则线段AD的长为___________.
15.如图,铁路路基横断面为一个等腰梯形,已知腰的坡度为,顶宽为,路基高为,那么路基的下底宽是______.
16.如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=_____.
17.如图,在矩形ABCD中,E为BC上一点,将AB沿AE折叠,使点B正好落在边CD上的点F处.若BE=3.AB=4,则sin∠FAD=___.
18.如图,在矩形ABCD中,AD=3,点E在AB边上,AE=4,BE=2,点F是AC上的一个动点.连接EF,将线段EF绕点E逆时针旋转90°并延长至其2倍,得到线段EG,当时,点G到CD的距离是 _______.
三、解答题(第19-20题每题7分,其余每题8分,共46分)
19.如图,海中有一个小岛A,小岛周围8海里范围内有暗礁,轮船在B点测得小岛A在北偏东45°方向上,轮船由西向东航行20海里到达D点,这时测得小岛A在北偏东方向上,求继续航行轮船是否有触礁危险?(参考数值:,).
20.如图,甲船在港口P的南偏西60°方向,距港口80海里的A处,沿AP方向以每小时18海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,已知两船同时出发,经过2小时乙船恰好在甲船的正东方向.求乙船的行驶速度.(结果保留根号)
21.如图,一楼房后有一假山,的坡度为,山坡坡面上点处有一休息亭,测得假山脚与楼房水平距离米,与亭子距离米,小丽从楼房房顶测得的俯角为.
(1)求点到水平地面的距离;
(2)求楼房的高.
22.如图,线段AB,DC分别表示甲、乙两建筑物的高,AB⊥BC于点B,DC⊥BC于点C,从点C测得A点的仰角α为60°,从D点测得A点的仰角β为30°,已知乙建筑物高DC=30m,求甲建筑物的高AB.
23.如图,在△ABC中,∠ACB=90°,sin A=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos ∠ABE的值.
24.如图是某幼儿园的两个同一水平面AF上的长度相同的滑梯模型图,已知滑梯斜面BC=EF=4m,∠ABC=30°,∠EFD=53°,且对角线CE所在的四边形是正方形.若小红从D﹣C﹣B再返回D处,小芳从D﹣C﹣E﹣F再返回D,试计算说明,小红和小芳谁走的路程更短,短多少?(精确到0.1m)(参考数据:sin53°≈,cos53°≈,tan53°≈, )
第二十八章 锐角三角函数 单元检测
一、单选题(每题3分,共18分)
1.在△ABC中,∠C=90°,sinB=,b=,则a等于( )
A. B.1 C.2 D.3
2.如图,在Rt△ABC中,,,,将△ABC绕点A逆时针旋转得到,使点落在AB边上,连结,则的值为( )
A. B. C. D.
3.如图,等腰中,交于点D,则的值为( )
A. B. C.3 D.
4.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35° B.mcos35° C. D.
5.如图,在中,,且.若,,则的长度为( )
A. B. C. D.8
6.如图,在中,,,,则的值为( )
A. B. C. D.
7.如图,在中,,则的值为( )
A. B. C. D.
8.如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则BD的值( )
A.2 B. C. D.5
9.如图,网格中小正方形的边长均为1,△ABC的顶点都在格点上,则cos∠BAC等于( )
A. B. C. D.
10.在中,、均为锐角,且,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
11.如图,一艘船由港沿北偏东65°方向航行至港,然后再沿北偏西40°方向航行至港,港在港北偏东20°方向,则,两港之间的距离为( ).
A. B. C. D.
12.如图,小明为了测量商业广场上的写字楼的高度,他从楼底部出发,沿楼前的广场前进到点,然后他沿坡度为∶的斜坡向上走米到达点,小明在此处观察点的仰角为,点A,B,,在同一平面内,若,则写字楼的高度约为( ).(结果精确到米.参考数据:,,,
A. B. C. D.
二、填空题(每题3分,共18分)
13.计算:cos45°= ________________
14.如图,在四边形中,,,,,则线段AD的长为___________.
15.如图,铁路路基横断面为一个等腰梯形,已知腰的坡度为,顶宽为,路基高为,那么路基的下底宽是______.
16.如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4,则S阴影=_____.
17.如图,在矩形ABCD中,E为BC上一点,将AB沿AE折叠,使点B正好落在边CD上的点F处.若BE=3.AB=4,则sin∠FAD=___.
18.如图,在矩形ABCD中,AD=3,点E在AB边上,AE=4,BE=2,点F是AC上的一个动点.连接EF,将线段EF绕点E逆时针旋转90°并延长至其2倍,得到线段EG,当时,点G到CD的距离是 _______.
三、解答题(第19-20题每题7分,其余每题8分,共46分)
19.如图,海中有一个小岛A,小岛周围8海里范围内有暗礁,轮船在B点测得小岛A在北偏东45°方向上,轮船由西向东航行20海里到达D点,这时测得小岛A在北偏东方向上,求继续航行轮船是否有触礁危险?(参考数值:,).
20.如图,甲船在港口P的南偏西60°方向,距港口80海里的A处,沿AP方向以每小时18海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,已知两船同时出发,经过2小时乙船恰好在甲船的正东方向.求乙船的行驶速度.(结果保留根号)
21.如图,一楼房后有一假山,的坡度为,山坡坡面上点处有一休息亭,测得假山脚与楼房水平距离米,与亭子距离米,小丽从楼房房顶测得的俯角为.
(1)求点到水平地面的距离;
(2)求楼房的高.
22.如图,线段AB,DC分别表示甲、乙两建筑物的高,AB⊥BC于点B,DC⊥BC于点C,从点C测得A点的仰角α为60°,从D点测得A点的仰角β为30°,已知乙建筑物高DC=30m,求甲建筑物的高AB.
23.如图,在△ABC中,∠ACB=90°,sin A=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos ∠ABE的值.
24.如图是某幼儿园的两个同一水平面AF上的长度相同的滑梯模型图,已知滑梯斜面BC=EF=4m,∠ABC=30°,∠EFD=53°,且对角线CE所在的四边形是正方形.若小红从D﹣C﹣B再返回D处,小芳从D﹣C﹣E﹣F再返回D,试计算说明,小红和小芳谁走的路程更短,短多少?(精确到0.1m)(参考数据:sin53°≈,cos53°≈,tan53°≈, )
