第六章特殊平行四边形大单元教学设计山东省泰安市东平县实验中学 52张PPT
文档属性
| 名称 | 第六章特殊平行四边形大单元教学设计山东省泰安市东平县实验中学 52张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 21:12:25 | ||
图片预览








文档简介
(共52张PPT)
大单元教学设计和作业设计
特殊平行四边形
整
体
结
构
“特殊平行四边形”主题单元结构包括“矩形”、“菱形”、“正方形”三部分,学生在初二平行四边形一章中,已经学习了三种特殊平行四边形:矩形、菱形和正方形,对三种图形的性质和判定已经了解并能运用这些知识解答简单的几何问题;并且在前一节的学习中,进行了对平行四边形性质和判定的证明,学生已掌握平行四边形的性质、判定及其应用,并且通过对命题证明的步骤回顾及对平行四边形性质和判定的证明,学生已掌握了了证明特殊平行四边形性质及判定定理的基本技能; 从而初步具备了证明特殊平行四边形性质和判定定理的能力;同时,在前面的相关学习活动中,学生已经初步了解了概括、转化及归纳等数学思想方法,大量的活动经验丰富了学生的数学思想,锻炼了学生的能力,使学生具备了在解题中合理运用方法的能力。
主
题
单
元
学
习
目
标
知识与技能:
理解平行四边形是中心对称图形,矩形、菱形、正方形都具有这样的特征
矩形、菱形、正方形作为特殊的平行四边形,不仅具有平行四边形的特征,还分别具有各自的特征,而且它们都是轴对称图形.
掌握特殊平行四边形的性质和判定,并能运用有关知识进行推理证明和计算边、角、对角线及面积;
通过知识的综合应用的说理,初步培养学生的逻辑思维能力.
主
题
单
元
学
习
目
标
过程与方法:
通过探索、归纳几类特殊四边形的特征和识别,了解它们之间的包含关系;
让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验;
通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力;
主
题
单
元
学
习
目
标
情感态度与价值观:
通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心。
对应课标
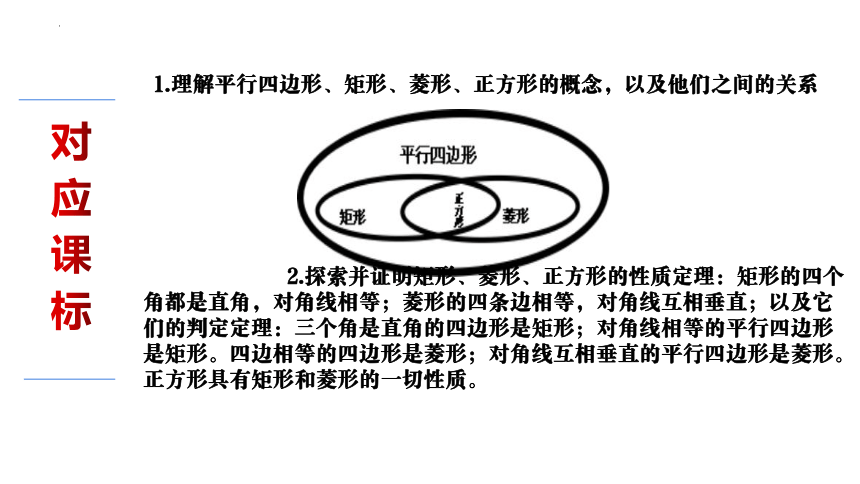
1.理解平行四边形、矩形、菱形、正方形的概念,以及他们之间的关系
2.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形。四边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形。正方形具有矩形和菱形的一切性质。
对应课标
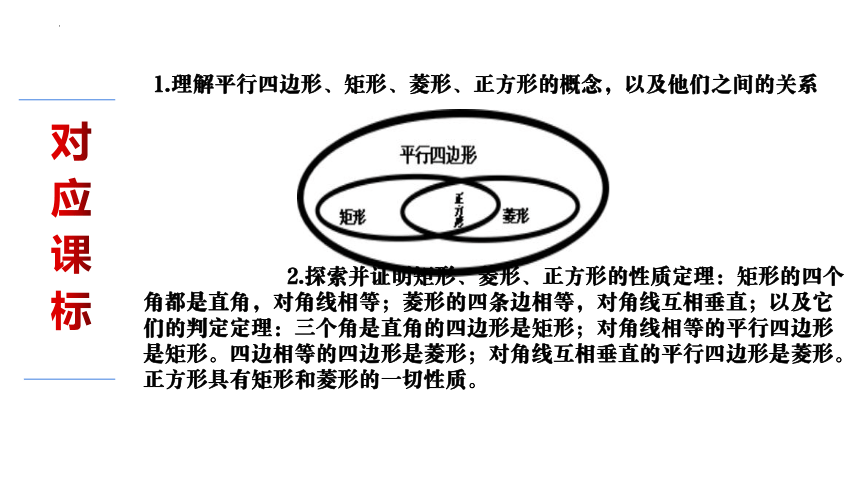
1.理解平行四边形、矩形、菱形、正方形的概念,以及他们之间的关系
2.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形。四边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形。正方形具有矩形和菱形的一切性质。
主
题
单
元
问
题
设
计
1.矩形、菱形、正方形的定义
2.矩形的边、角、对角线有怎样的特征?矩形有怎样的性质?3.菱形的边、角、对角线有怎样的特征?菱形有怎样的性质?4.学习了矩形、菱形的性质,正方形的性质呢?5.单独地从边或角或对角线,能否判断出一个四边形是矩形? 能否判断出一个平行四边形是矩形? 如何判断一个四边形或者平行四边形是矩形?6.如何判断一个四边形或者平行四边形是菱形?7.如何判断一个矩形是正方形? 如何判断一个菱形是正方形? 如何判断一个平行四边形是正方形? 如何判断一个四边形是正方形?
01
03
02
专题一
专题三
专题二
矩形的性质及判定
(课内2课时,课外1课时)
菱形的性质及判定
(课内2课时,课外1课时)
正方形的性质及判定
(课内2课时,课外1课时)
专题划分
1
专题一
矩形的性质及判定
(课内2课时,课外1课时)
专题学习目标
知识与技能: 理解矩形是中心对称图形 矩形作为特殊平行四边形,不仅具有平行四边形的特征,还具有自身的特征,而且它是轴对称图形. 掌握矩形的性质和判定,并能运用有关知识进行推理证明和计算 掌握直角三角形斜边上的中线的性质与应用
过程与方法: 了解矩形与平行四边形间的包含关系; 让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验; 通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力;
情感态度与价值观: 通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心;
1
2
3
4
5
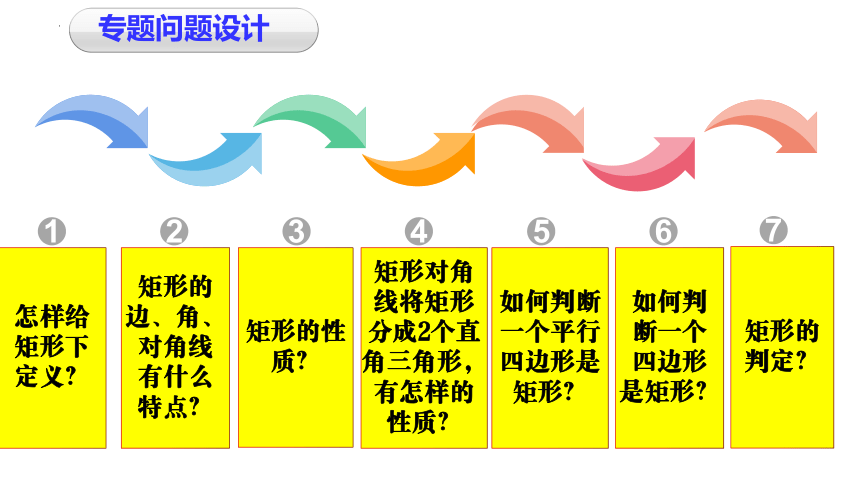
怎样给矩形下定义?
矩形的边、角、对角线有什么特点?
矩形的性质?
矩形对角线将矩形分成2个直角三角形,有怎样的性质?
如何判断一个平行四边形是矩形?
6
如何判断一个四边形是矩形?
专题问题设计
7
矩形的判定?
所需教学材料和资源
作图工具(直尺、三角板、圆规等)
常规资源
多媒体教室 ,几何画板软件
PPT , 几何画板课件。
信息化资源
纸笔等。
其 他
教学支撑环境
学习活动设计
第一课时 矩形的性质 活动一:说说生活中的矩形 【活动步骤】 1.结合图,回顾矩形定义
2.举出几个生活中矩形的例子.
学习活动设计
活动二:探索矩形的一般性质(即平行四边形所有性质)
【活动步骤】
1. 小组合作,矩形的边、角、对角线有什么特点?
2. 个人思考:矩形的一般性质?小组交流,形成共识.
活动三:探索矩形的特殊性质
1.引导学生猜想: 猜想1: 猜想2:
2.教师引导小组合作,推导性质定理
活动四:探索直角三角形斜边中线性质定理
1.教师引导:对角线将矩形分成几个直角三角形?
每个直角三角形出现了哪条边的中线?
这条中线与矩形的对角线有什么大小关系?与斜边呢?
2.学生得出直角三角形斜边中线性质定理
学习活动设计
第二课时:矩形的判定
活动一:探究平行四边形到矩形的转化
【活动步骤】
1. 提出问题:矩形的性质有:四个角都是直角,对角线相等且互相平分,那么什么样的平行四边形是矩形?
2.指导学生探究,交流。
3.指导学生利用几何画板的功能展示由平行四边形到矩形的探究过程.
【技术应用】
几何画板探究平行四边形到矩形的过程
使用专门制作的几何画板课件探究、演示.
学习活动设计
第二课时:矩形的判定
活动二:探究四边形到菱形的转化
【活动步骤】
1.指导学生结合课件猜测相应结论;
2.组织学生交流,总结结论、方法.
活动三:推导矩形判定定理
【活动步骤】
1.写出命题
2.思考:证明命题的步骤
3.推理得出矩形的判定定理
【技术应用】
使用专门制作的几何画板课件探究、演示.
学习活动设计
第三课时(课外) 测量矩形
活动一:想一想
1.如何利用1把直角三角板测量出一个模型是否是矩形?
2.如何只利用圆规测量出一个模型是否是矩形?
活动二:展示成果
测法展示交流.
4
STEP
数学问题生活化
3
STEP
学生是否主动参与、主动探索、主动思考、主动实践
2
STEP
学生是否充分经历知识形成的全过程
1
STEP
学生观察、交流、分析、归纳的如何
评价要点
2
专题二
菱形的性质及判定
(课内2课时,课外1课时)
专题学习目标
知识与技能: 理解菱形是中心对称图形
菱形作为特殊的平行四边形,不仅具有平行四边形的特征,还分别具有各自的特征,而且是轴对称图形.
掌握菱形的性质和判定,并能运用有关知识进行推理证明和计算;
过程与方法: 通过探索、归纳菱形的特征,识别、了解它与平行四边形之间的包含关系。
让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验。
通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力。
情感态度与价值观: 通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心
1
2
3
4
5
怎样给菱形下定义?
菱形的边、角、对角线有什么特点?
菱形的性质?
如何根据菱形性质对边、角、对角线进行有关计算?如何计算菱形面积?
如何判断一个平行四边形是菱形?
6
如何判断一个四边形是菱形?
专题问题设计
7
菱形的的判定?
所需教学材料和资源
作图工具(直尺、三角板、圆规等)
常规资源
多媒体教室 ,几何画板软件
PPT , 几何画板课件。
信息化资源
纸笔等。
其 他
教学支撑环境
学习活动设计
第一课时 菱形的性质 活动1:温故知新
1.平行四边形的性质
2.矩形的性质
活动2:想一想
【活动步骤】
1.在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
(1)每个学生思考什么是菱形;
(2)小组合作,组内交流各自的想法;
2.类比矩形的定义,给菱形下定义
个人思考,组内交流,班内交流.
学习活动设计
活动3:感受生活
【活动步骤】
1.说一说生活中的菱形
2.教师展示部分图片
【技术应用】在PPT中动态演示菱形
学习活动设计
活动4:认识菱形
【活动步骤】
教师点拨:1.菱形是中心对称图形么?是轴对称图形么?
【技术应用】几何画板演示菱形的中心对称和轴对称性
学习活动设计
活动5:探究菱形性质
1.菱形的边有什么特性?
菱形的角有什么特性?
菱形的对角线有什么特性?
2.学生总结菱形的性质
活动6:求菱形面积
1.引导学生求菱形面积的发现
2.得出菱形面积公式(2种算法)
学习活动设计
第二课时:菱形的判定
活动一:探究平行四边形到菱形的转化
【活动步骤】
1.提出问题:菱形的性质有四条边都相等,对边平行且相等,那么什么样的平行四边形是菱形
2.提出问题:菱形的性质有对角线互相垂直平分,那么什么样的平行四边形是菱形?
3.指导学生探究,交流。
4.指导学生利用几何画板的功能展示有平行四边形到菱形的探究过程.
【技术应用】
几何画板探究平行四边形到菱形的过程
学习活动设计
第二课时:菱形的判定
活动二:探究四边形到菱形的转化
【活动步骤】
1.指导学生结合课件猜测相应结论;
2.组织学生交流,总结结论、方法.
活动三:推导菱形判定定理
【活动步骤】
1.写出命题
2.思考:证明命题的步骤
3.推理得出菱形的判定定理
【技术应用】使用专门制作的几何画板课件探究、演示.
学习活动设计
第三课时(课外) 折叠菱形
活动一:折一折 剪一剪
1.如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
2.组内交流
活动二:展示成果
1.作品展示交流.
2.说明下面这问同学剪法的依据.
评价要点
菱形的性质定理和面积的求法是关键,可以通过小测、谈话、调查问卷、评价等多种形式,对学生掌握情况有个量的标准,结合《新课标》的有关规定,有的放矢地指导学生。
3
专题三
正方形的性质及判定
(课内2课时,课外1课时)
专题学习目标
知识与技能: 理解正方形既是中心对称图形又是轴对称图形
正方形作为特殊的平行四边形,不仅具有矩形的特征,又具有菱形的特征,还具有自己的特征.
掌握正方形的性质和判定,并能运用有关知识进行推理证明和计算;
过程与方法: 通过探索、归纳正方形的特征,识别、了解它与平行四边形之间的包含关系。
让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验。
通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力。
情感态度与价值观: 通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心
1
2
3
4
5
怎样给正方形下定义?
正方形的边、角、对角线有什么特点?
正方形的性质?
如何根据正方形性质对边、角、对角线进行有关计算?如何计算正方形面积?
如何判断一个平行四边形是正方形?
6
如何判断一个四边形是正方形?
专题问题设计
7
正方形的的判定?
所需教学材料和资源
作图工具(直尺、三角板、圆规等)
常规资源
多媒体教室 ,几何画板软件
PPT , 几何画板课件。
信息化资源
纸笔等。
其 他
教学支撑环境
学习活动设计
第一课时 正方形的性质 活动1:温故知新
1.平行四边形的性质
2.矩形的性质
3.菱形的性质
活动2:想一想
【活动步骤】
1.在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
(1)每个学生思考什么是正方形;
(2)小组合作,组内交流各自的想法;
2.类比矩形、菱形的定义,给正方形下定义
个人思考,组内交流,班内交流.
学习活动设计
活动3:感受生活
【活动步骤】
1.说一说生活中的正方形
2.教师展示部分图片
【技术应用】在PPT中动态演示正方形
活动4:认识正方形
【活动步骤】
教师点拨:1.正方形是中心对称图形么?是轴对称图形么?
【技术应用】几何画板演示正方形的中心对称和轴对称性
活动5:探究正方形性质
1.正方形的边、角、对角线有什么特性?
2.学生总结正方形的性质
学习活动设计
第二课时:正方形的判定
活动一:探究平行四边形到正方形的转化
【活动步骤】
1.提出问题:正方形的性质
2.指导学生探究,交流。
3.指导学生利用几何画板的功能展示有平行四边形到菱形的探究过程.
【技术应用】
几何画板探究平行四边形到菱形的过程
学习活动设计
第二课时:菱形的判定
活动二:探究菱形到正方形的转化
探究矩形到正方形的转化
探究四边形到正方形的转化
【活动步骤】
1.指导学生结合课件猜测相应结论;
2.组织学生交流,总结结论、方法.
活动三:推导正方形判定定理
【活动步骤】
1.写出命题
2.思考:证明命题的步骤
3.推理得出正方形的判定定理
【技术应用】使用专门制作的几何画板课件探究、演示.
学习活动设计
第三课时(课外) 我是一名优秀设计师
在一块正方形花坛上,欲修建两条直的小路,使得两条直的小路将花坛分成全等的四部分(不考虑道路宽度),你有几种方法?(至少说出三种)
评价要点
正方形的性质定理和判定定理是关键,可以通过小测、谈话、调查问卷、评价等多种形式,对学生掌握情况有个量的标准,结合《新课标》的有关规定,有的放矢地指导学生。
四边形
矩形
平行四边形
菱形
正方形
说一说
4
大单元作业设计
基础达标题
一、选择:
1、正方形具有而菱形不一定具有的性质( )
A、四边都相等 B、对角线互相垂直且平分
C、对角线相等 D、对角线平分一组对角
2、下列命题中( )是假命题.
A、对角线互相平分的四边形是平行四边形.
B、两条对角线相等的四边形是矩形.
C、两条对角线互相垂直的矩形是正方形.
D、两条对角线相等的菱形是正方形.
C
B
基础达标题
二、填空:
1、菱形的对角线长为6和8,则菱形的边长___,面积是___.
2、矩形的对角线长为8,两对角线的夹角为60 ,则矩形的两邻边分别长___和___.
A
B
C
D
A
O
O
B
C
D
你准行
1题
2题
基础达标题
思考巩固题
归纳总结题
归纳总结题
能力提升题
能力提升题
能力提升题
大单元教学设计和作业设计
特殊平行四边形
整
体
结
构
“特殊平行四边形”主题单元结构包括“矩形”、“菱形”、“正方形”三部分,学生在初二平行四边形一章中,已经学习了三种特殊平行四边形:矩形、菱形和正方形,对三种图形的性质和判定已经了解并能运用这些知识解答简单的几何问题;并且在前一节的学习中,进行了对平行四边形性质和判定的证明,学生已掌握平行四边形的性质、判定及其应用,并且通过对命题证明的步骤回顾及对平行四边形性质和判定的证明,学生已掌握了了证明特殊平行四边形性质及判定定理的基本技能; 从而初步具备了证明特殊平行四边形性质和判定定理的能力;同时,在前面的相关学习活动中,学生已经初步了解了概括、转化及归纳等数学思想方法,大量的活动经验丰富了学生的数学思想,锻炼了学生的能力,使学生具备了在解题中合理运用方法的能力。
主
题
单
元
学
习
目
标
知识与技能:
理解平行四边形是中心对称图形,矩形、菱形、正方形都具有这样的特征
矩形、菱形、正方形作为特殊的平行四边形,不仅具有平行四边形的特征,还分别具有各自的特征,而且它们都是轴对称图形.
掌握特殊平行四边形的性质和判定,并能运用有关知识进行推理证明和计算边、角、对角线及面积;
通过知识的综合应用的说理,初步培养学生的逻辑思维能力.
主
题
单
元
学
习
目
标
过程与方法:
通过探索、归纳几类特殊四边形的特征和识别,了解它们之间的包含关系;
让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验;
通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力;
主
题
单
元
学
习
目
标
情感态度与价值观:
通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心。
对应课标
1.理解平行四边形、矩形、菱形、正方形的概念,以及他们之间的关系
2.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形。四边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形。正方形具有矩形和菱形的一切性质。
对应课标
1.理解平行四边形、矩形、菱形、正方形的概念,以及他们之间的关系
2.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形。四边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形。正方形具有矩形和菱形的一切性质。
主
题
单
元
问
题
设
计
1.矩形、菱形、正方形的定义
2.矩形的边、角、对角线有怎样的特征?矩形有怎样的性质?3.菱形的边、角、对角线有怎样的特征?菱形有怎样的性质?4.学习了矩形、菱形的性质,正方形的性质呢?5.单独地从边或角或对角线,能否判断出一个四边形是矩形? 能否判断出一个平行四边形是矩形? 如何判断一个四边形或者平行四边形是矩形?6.如何判断一个四边形或者平行四边形是菱形?7.如何判断一个矩形是正方形? 如何判断一个菱形是正方形? 如何判断一个平行四边形是正方形? 如何判断一个四边形是正方形?
01
03
02
专题一
专题三
专题二
矩形的性质及判定
(课内2课时,课外1课时)
菱形的性质及判定
(课内2课时,课外1课时)
正方形的性质及判定
(课内2课时,课外1课时)
专题划分
1
专题一
矩形的性质及判定
(课内2课时,课外1课时)
专题学习目标
知识与技能: 理解矩形是中心对称图形 矩形作为特殊平行四边形,不仅具有平行四边形的特征,还具有自身的特征,而且它是轴对称图形. 掌握矩形的性质和判定,并能运用有关知识进行推理证明和计算 掌握直角三角形斜边上的中线的性质与应用
过程与方法: 了解矩形与平行四边形间的包含关系; 让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验; 通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力;
情感态度与价值观: 通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心;
1
2
3
4
5
怎样给矩形下定义?
矩形的边、角、对角线有什么特点?
矩形的性质?
矩形对角线将矩形分成2个直角三角形,有怎样的性质?
如何判断一个平行四边形是矩形?
6
如何判断一个四边形是矩形?
专题问题设计
7
矩形的判定?
所需教学材料和资源
作图工具(直尺、三角板、圆规等)
常规资源
多媒体教室 ,几何画板软件
PPT , 几何画板课件。
信息化资源
纸笔等。
其 他
教学支撑环境
学习活动设计
第一课时 矩形的性质 活动一:说说生活中的矩形 【活动步骤】 1.结合图,回顾矩形定义
2.举出几个生活中矩形的例子.
学习活动设计
活动二:探索矩形的一般性质(即平行四边形所有性质)
【活动步骤】
1. 小组合作,矩形的边、角、对角线有什么特点?
2. 个人思考:矩形的一般性质?小组交流,形成共识.
活动三:探索矩形的特殊性质
1.引导学生猜想: 猜想1: 猜想2:
2.教师引导小组合作,推导性质定理
活动四:探索直角三角形斜边中线性质定理
1.教师引导:对角线将矩形分成几个直角三角形?
每个直角三角形出现了哪条边的中线?
这条中线与矩形的对角线有什么大小关系?与斜边呢?
2.学生得出直角三角形斜边中线性质定理
学习活动设计
第二课时:矩形的判定
活动一:探究平行四边形到矩形的转化
【活动步骤】
1. 提出问题:矩形的性质有:四个角都是直角,对角线相等且互相平分,那么什么样的平行四边形是矩形?
2.指导学生探究,交流。
3.指导学生利用几何画板的功能展示由平行四边形到矩形的探究过程.
【技术应用】
几何画板探究平行四边形到矩形的过程
使用专门制作的几何画板课件探究、演示.
学习活动设计
第二课时:矩形的判定
活动二:探究四边形到菱形的转化
【活动步骤】
1.指导学生结合课件猜测相应结论;
2.组织学生交流,总结结论、方法.
活动三:推导矩形判定定理
【活动步骤】
1.写出命题
2.思考:证明命题的步骤
3.推理得出矩形的判定定理
【技术应用】
使用专门制作的几何画板课件探究、演示.
学习活动设计
第三课时(课外) 测量矩形
活动一:想一想
1.如何利用1把直角三角板测量出一个模型是否是矩形?
2.如何只利用圆规测量出一个模型是否是矩形?
活动二:展示成果
测法展示交流.
4
STEP
数学问题生活化
3
STEP
学生是否主动参与、主动探索、主动思考、主动实践
2
STEP
学生是否充分经历知识形成的全过程
1
STEP
学生观察、交流、分析、归纳的如何
评价要点
2
专题二
菱形的性质及判定
(课内2课时,课外1课时)
专题学习目标
知识与技能: 理解菱形是中心对称图形
菱形作为特殊的平行四边形,不仅具有平行四边形的特征,还分别具有各自的特征,而且是轴对称图形.
掌握菱形的性质和判定,并能运用有关知识进行推理证明和计算;
过程与方法: 通过探索、归纳菱形的特征,识别、了解它与平行四边形之间的包含关系。
让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验。
通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力。
情感态度与价值观: 通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心
1
2
3
4
5
怎样给菱形下定义?
菱形的边、角、对角线有什么特点?
菱形的性质?
如何根据菱形性质对边、角、对角线进行有关计算?如何计算菱形面积?
如何判断一个平行四边形是菱形?
6
如何判断一个四边形是菱形?
专题问题设计
7
菱形的的判定?
所需教学材料和资源
作图工具(直尺、三角板、圆规等)
常规资源
多媒体教室 ,几何画板软件
PPT , 几何画板课件。
信息化资源
纸笔等。
其 他
教学支撑环境
学习活动设计
第一课时 菱形的性质 活动1:温故知新
1.平行四边形的性质
2.矩形的性质
活动2:想一想
【活动步骤】
1.在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
(1)每个学生思考什么是菱形;
(2)小组合作,组内交流各自的想法;
2.类比矩形的定义,给菱形下定义
个人思考,组内交流,班内交流.
学习活动设计
活动3:感受生活
【活动步骤】
1.说一说生活中的菱形
2.教师展示部分图片
【技术应用】在PPT中动态演示菱形
学习活动设计
活动4:认识菱形
【活动步骤】
教师点拨:1.菱形是中心对称图形么?是轴对称图形么?
【技术应用】几何画板演示菱形的中心对称和轴对称性
学习活动设计
活动5:探究菱形性质
1.菱形的边有什么特性?
菱形的角有什么特性?
菱形的对角线有什么特性?
2.学生总结菱形的性质
活动6:求菱形面积
1.引导学生求菱形面积的发现
2.得出菱形面积公式(2种算法)
学习活动设计
第二课时:菱形的判定
活动一:探究平行四边形到菱形的转化
【活动步骤】
1.提出问题:菱形的性质有四条边都相等,对边平行且相等,那么什么样的平行四边形是菱形
2.提出问题:菱形的性质有对角线互相垂直平分,那么什么样的平行四边形是菱形?
3.指导学生探究,交流。
4.指导学生利用几何画板的功能展示有平行四边形到菱形的探究过程.
【技术应用】
几何画板探究平行四边形到菱形的过程
学习活动设计
第二课时:菱形的判定
活动二:探究四边形到菱形的转化
【活动步骤】
1.指导学生结合课件猜测相应结论;
2.组织学生交流,总结结论、方法.
活动三:推导菱形判定定理
【活动步骤】
1.写出命题
2.思考:证明命题的步骤
3.推理得出菱形的判定定理
【技术应用】使用专门制作的几何画板课件探究、演示.
学习活动设计
第三课时(课外) 折叠菱形
活动一:折一折 剪一剪
1.如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
2.组内交流
活动二:展示成果
1.作品展示交流.
2.说明下面这问同学剪法的依据.
评价要点
菱形的性质定理和面积的求法是关键,可以通过小测、谈话、调查问卷、评价等多种形式,对学生掌握情况有个量的标准,结合《新课标》的有关规定,有的放矢地指导学生。
3
专题三
正方形的性质及判定
(课内2课时,课外1课时)
专题学习目标
知识与技能: 理解正方形既是中心对称图形又是轴对称图形
正方形作为特殊的平行四边形,不仅具有矩形的特征,又具有菱形的特征,还具有自己的特征.
掌握正方形的性质和判定,并能运用有关知识进行推理证明和计算;
过程与方法: 通过探索、归纳正方形的特征,识别、了解它与平行四边形之间的包含关系。
让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验。
通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力。
情感态度与价值观: 通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心
1
2
3
4
5
怎样给正方形下定义?
正方形的边、角、对角线有什么特点?
正方形的性质?
如何根据正方形性质对边、角、对角线进行有关计算?如何计算正方形面积?
如何判断一个平行四边形是正方形?
6
如何判断一个四边形是正方形?
专题问题设计
7
正方形的的判定?
所需教学材料和资源
作图工具(直尺、三角板、圆规等)
常规资源
多媒体教室 ,几何画板软件
PPT , 几何画板课件。
信息化资源
纸笔等。
其 他
教学支撑环境
学习活动设计
第一课时 正方形的性质 活动1:温故知新
1.平行四边形的性质
2.矩形的性质
3.菱形的性质
活动2:想一想
【活动步骤】
1.在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
(1)每个学生思考什么是正方形;
(2)小组合作,组内交流各自的想法;
2.类比矩形、菱形的定义,给正方形下定义
个人思考,组内交流,班内交流.
学习活动设计
活动3:感受生活
【活动步骤】
1.说一说生活中的正方形
2.教师展示部分图片
【技术应用】在PPT中动态演示正方形
活动4:认识正方形
【活动步骤】
教师点拨:1.正方形是中心对称图形么?是轴对称图形么?
【技术应用】几何画板演示正方形的中心对称和轴对称性
活动5:探究正方形性质
1.正方形的边、角、对角线有什么特性?
2.学生总结正方形的性质
学习活动设计
第二课时:正方形的判定
活动一:探究平行四边形到正方形的转化
【活动步骤】
1.提出问题:正方形的性质
2.指导学生探究,交流。
3.指导学生利用几何画板的功能展示有平行四边形到菱形的探究过程.
【技术应用】
几何画板探究平行四边形到菱形的过程
学习活动设计
第二课时:菱形的判定
活动二:探究菱形到正方形的转化
探究矩形到正方形的转化
探究四边形到正方形的转化
【活动步骤】
1.指导学生结合课件猜测相应结论;
2.组织学生交流,总结结论、方法.
活动三:推导正方形判定定理
【活动步骤】
1.写出命题
2.思考:证明命题的步骤
3.推理得出正方形的判定定理
【技术应用】使用专门制作的几何画板课件探究、演示.
学习活动设计
第三课时(课外) 我是一名优秀设计师
在一块正方形花坛上,欲修建两条直的小路,使得两条直的小路将花坛分成全等的四部分(不考虑道路宽度),你有几种方法?(至少说出三种)
评价要点
正方形的性质定理和判定定理是关键,可以通过小测、谈话、调查问卷、评价等多种形式,对学生掌握情况有个量的标准,结合《新课标》的有关规定,有的放矢地指导学生。
四边形
矩形
平行四边形
菱形
正方形
说一说
4
大单元作业设计
基础达标题
一、选择:
1、正方形具有而菱形不一定具有的性质( )
A、四边都相等 B、对角线互相垂直且平分
C、对角线相等 D、对角线平分一组对角
2、下列命题中( )是假命题.
A、对角线互相平分的四边形是平行四边形.
B、两条对角线相等的四边形是矩形.
C、两条对角线互相垂直的矩形是正方形.
D、两条对角线相等的菱形是正方形.
C
B
基础达标题
二、填空:
1、菱形的对角线长为6和8,则菱形的边长___,面积是___.
2、矩形的对角线长为8,两对角线的夹角为60 ,则矩形的两邻边分别长___和___.
A
B
C
D
A
O
O
B
C
D
你准行
1题
2题
基础达标题
思考巩固题
归纳总结题
归纳总结题
能力提升题
能力提升题
能力提升题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
