3.2一定是直角三角形吗 课件(共18张PPT)
文档属性
| 名称 | 3.2一定是直角三角形吗 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 13:19:45 | ||
图片预览





文档简介
(共18张PPT)
一定是直角三角形吗
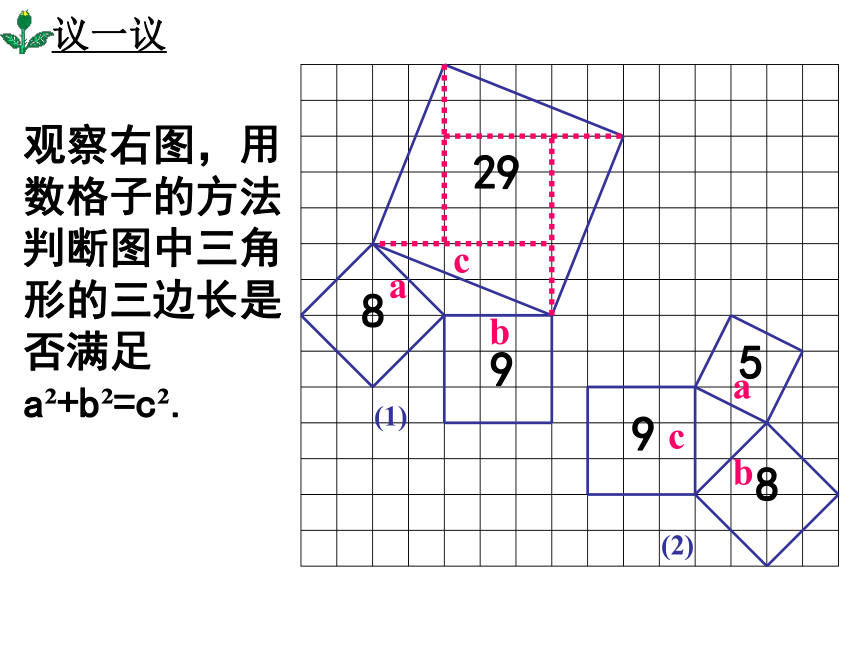
议一议
a
b
c
b
a
c
(1)
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
29
8
9
9
5
8
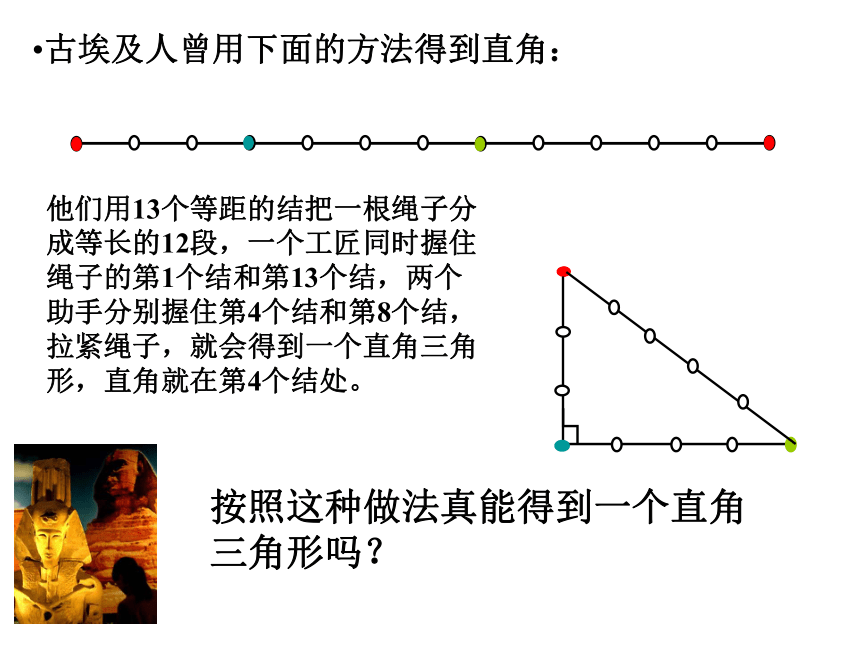
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,直角就在第4个结处。
教学目标
1、掌握直角三角形的判别条件(即勾股定理的逆定理),并能进行简单应用。
2、理解勾股定理和勾股定理的逆定理之间的区别。
问题1:直角三角形有哪些性质
①有一个内角为直角;②两个锐角互余;
③两条直角边的平方和等于斜边的平方.
问题2:反过来,一个三角形,满足什么条件
就是直角三角形呢?
如果有一个内角是直角,它就是直角三角形.
如果有两个角的和是90°,
那么这个三角形也是直角三角形
我们刚学习了勾股定理,知道一个直角三角形的两直角边a,b,斜边c具有一定的数量关系即a2+b2=c2.我们是否也可以不用角,而用三角形三边的关系来判定它是否为直角三角形呢?
下面有三组数分别是一个三角形的三边长a,b,c:
①5,12,13; ②7,24,25; ③8,15,17.
回答这样两个问题:
1.这三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
从刚才的分组实验,有什么样的结论发现吗?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
提问1 同学们还能找出哪些勾股数呢?
提问2 到今天为止,你能用哪些方法判断一个三角形是直角三角形呢?
如果三角形的三边长a,b,c满a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.
1. 如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是 ( )
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
B
A
一组勾股数的倍数一定是勾股数吗?为什么
判断:
1、由于0.3,0.4,0.5不是勾股数,所以0.3,0.4,0.5为边长的三角形不是直角三角形( )
2、由于0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数( )
填空:
1、已知 三角形的三边分别为5,12,13,则这个三角形是( )
直角三角形
2、三条线段 m,n,p满足m2-n2=p2 ,以这三条线段为边组成的三角形为( )
直角三角形
登高望远
1.一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
解答:符合要求 ,
∵ _ ∴∠A=90°,又∵_
∴∠DBC=90°
1.如图,在正方形ABCD中,AB=4,AE=2, DF=1,
图中有几个直角三角形,你是如何判断的?与你的同
伴交流。
4
1
2
2
4
3
2.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
答案:
④⑤是直角三角形
①②③⑥不是直角三角形
1.下列几组数据能否作为直角三角形的三边?
(1)9,12,15; (2)15,36,39;
(3)12,35,36 ; (4)12,18,22.
2.一个三角形的三边的长分别是15cm,20cm,
25cm,则这个三角形的面积是( )cm2 .
(A)250 (B)150 (C)200 (D)不能确定
3.如图,在△ABC中,AD⊥BC于D,BD=9,
AD=12,AC=20,则△ABC是( ).
(A)等腰三角形 (B)锐角三角形
(C)钝角三角形 (D)直角三角形
4.将直角三角形的三边同时扩大相同的倍数
后,得到的三角形是( ).
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)不能确定
A
B
D
C
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2,
那么这个三角形是直角三角形
勾股数:
满足a2 +b2=c2的三个正整数,称为勾股数
小结
当堂达标
见导学案
一定是直角三角形吗
议一议
a
b
c
b
a
c
(1)
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
29
8
9
9
5
8
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,直角就在第4个结处。
教学目标
1、掌握直角三角形的判别条件(即勾股定理的逆定理),并能进行简单应用。
2、理解勾股定理和勾股定理的逆定理之间的区别。
问题1:直角三角形有哪些性质
①有一个内角为直角;②两个锐角互余;
③两条直角边的平方和等于斜边的平方.
问题2:反过来,一个三角形,满足什么条件
就是直角三角形呢?
如果有一个内角是直角,它就是直角三角形.
如果有两个角的和是90°,
那么这个三角形也是直角三角形
我们刚学习了勾股定理,知道一个直角三角形的两直角边a,b,斜边c具有一定的数量关系即a2+b2=c2.我们是否也可以不用角,而用三角形三边的关系来判定它是否为直角三角形呢?
下面有三组数分别是一个三角形的三边长a,b,c:
①5,12,13; ②7,24,25; ③8,15,17.
回答这样两个问题:
1.这三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
从刚才的分组实验,有什么样的结论发现吗?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
提问1 同学们还能找出哪些勾股数呢?
提问2 到今天为止,你能用哪些方法判断一个三角形是直角三角形呢?
如果三角形的三边长a,b,c满a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.
1. 如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是 ( )
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
B
A
一组勾股数的倍数一定是勾股数吗?为什么
判断:
1、由于0.3,0.4,0.5不是勾股数,所以0.3,0.4,0.5为边长的三角形不是直角三角形( )
2、由于0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数( )
填空:
1、已知 三角形的三边分别为5,12,13,则这个三角形是( )
直角三角形
2、三条线段 m,n,p满足m2-n2=p2 ,以这三条线段为边组成的三角形为( )
直角三角形
登高望远
1.一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
解答:符合要求 ,
∵ _ ∴∠A=90°,又∵_
∴∠DBC=90°
1.如图,在正方形ABCD中,AB=4,AE=2, DF=1,
图中有几个直角三角形,你是如何判断的?与你的同
伴交流。
4
1
2
2
4
3
2.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
答案:
④⑤是直角三角形
①②③⑥不是直角三角形
1.下列几组数据能否作为直角三角形的三边?
(1)9,12,15; (2)15,36,39;
(3)12,35,36 ; (4)12,18,22.
2.一个三角形的三边的长分别是15cm,20cm,
25cm,则这个三角形的面积是( )cm2 .
(A)250 (B)150 (C)200 (D)不能确定
3.如图,在△ABC中,AD⊥BC于D,BD=9,
AD=12,AC=20,则△ABC是( ).
(A)等腰三角形 (B)锐角三角形
(C)钝角三角形 (D)直角三角形
4.将直角三角形的三边同时扩大相同的倍数
后,得到的三角形是( ).
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)不能确定
A
B
D
C
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2,
那么这个三角形是直角三角形
勾股数:
满足a2 +b2=c2的三个正整数,称为勾股数
小结
当堂达标
见导学案
