3.1.1探索勾股定理1 课件(共20张PPT)
文档属性
| 名称 | 3.1.1探索勾股定理1 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 13:43:38 | ||
图片预览





文档简介
(共20张PPT)
探索勾股定理1
你想知道吗
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
探索勾股定理
教学目标
1.掌握用数格子(或割、补、拼等)的办法体验勾股定理的探索过程;
2.理解勾股定理反映的直角三角形的三边之间的数量关系;
3.认识勾股定理的各种探究方法.
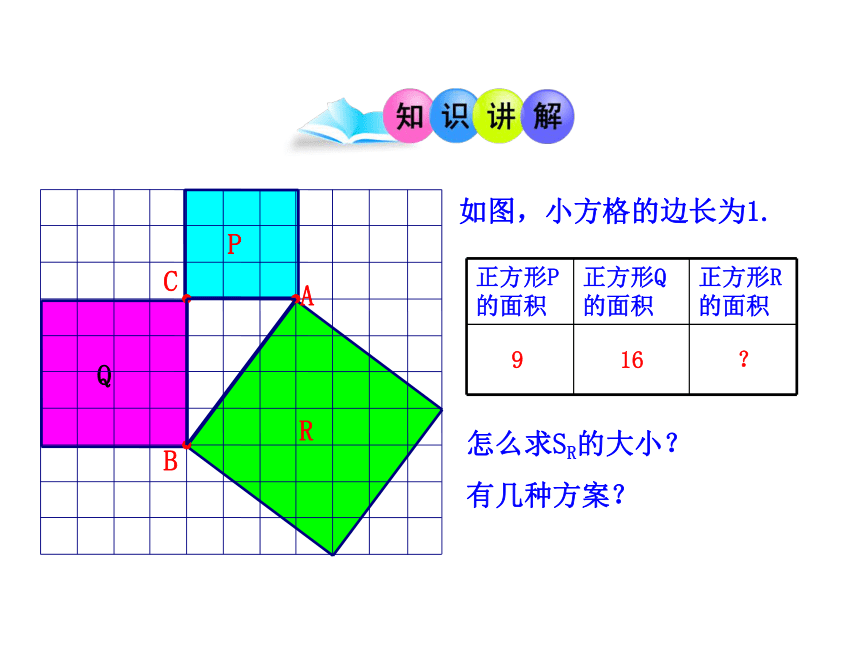
P
R
Q
正方形P的面积 正方形Q的面积 正方形R的面积
A
B
C
9
16
?
怎么求SR的大小?
有几种方案?
如图,小方格的边长为1.
P
Q
C
R
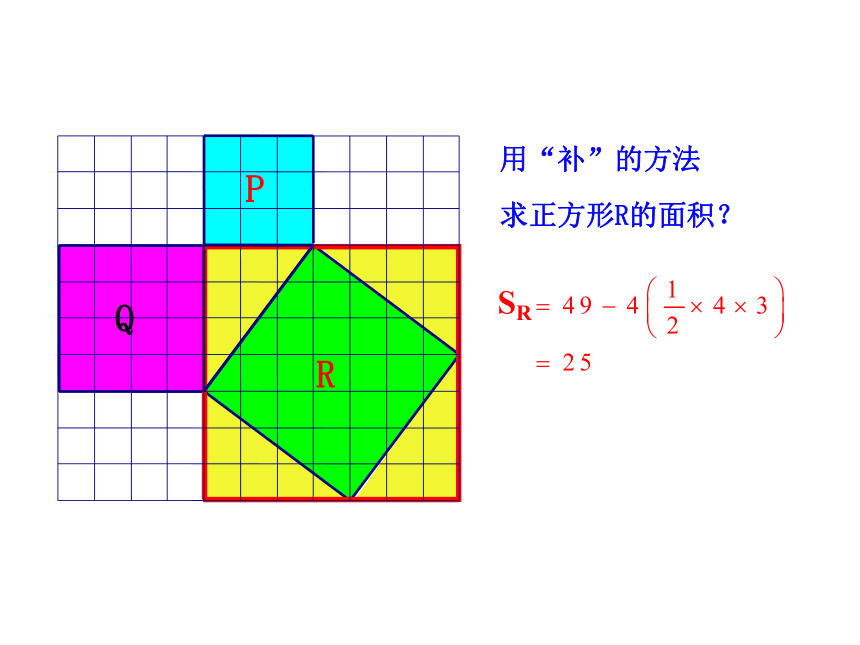
求正方形R的面积?
用“补”的方法
SR
P
Q
C
R
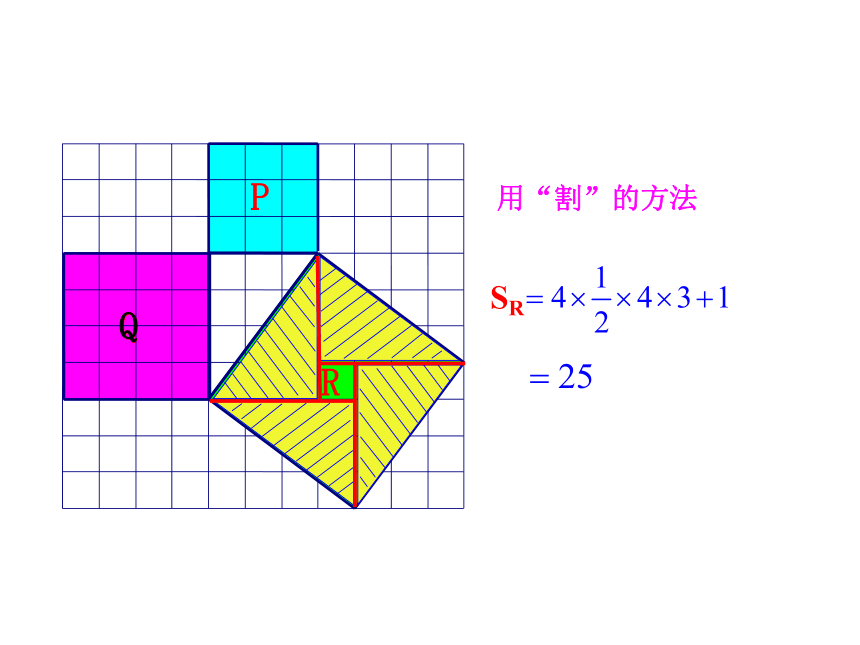
用“割”的方法
Q
SR
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
(1)在图中,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是____个
单位面积.
正方形C的面积是_____
个单位面积.
9
9
9
18
(2)(3)
探究勾股定理
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
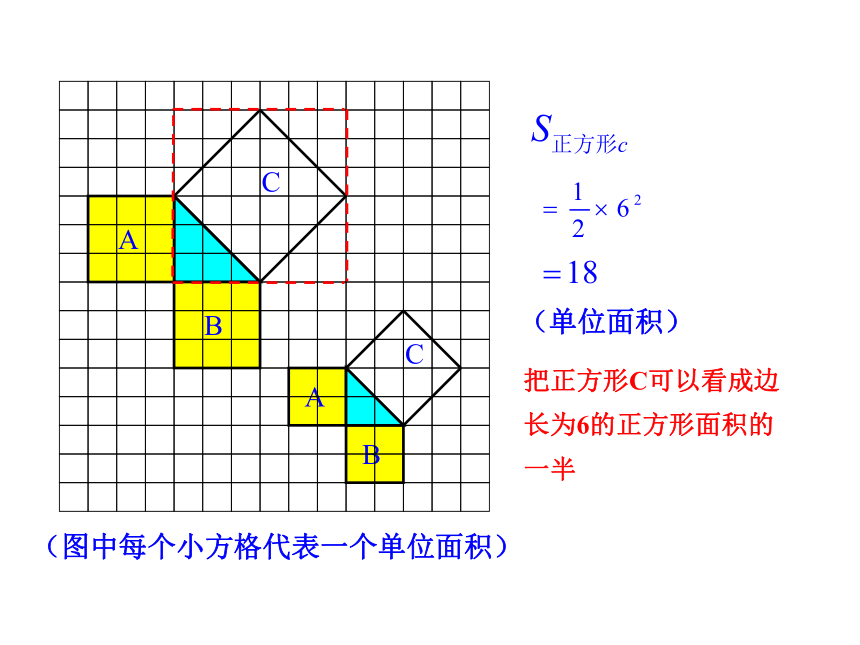
把正方形C分割成若干个直角边为整数的三角形来求
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
(单位面积)
把正方形C可以看成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?图2呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
A
B
C
图1
A
B
C
图2
(1)观察图1、图2,并填写右表:
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1
图2
16
9
25
4
9
13
做一做
A
B
C
图1
A
B
C
图2
(2)右图中正方形A,B,C的面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
A
B
C
SA=a2
SB=b2
SC=c2
a
b
c
a2+b2=c2
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
SA+SB=SC
探索勾股定理
中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.
据《周髀算经》记载,西周战国时期(约公元1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.
3
4
5
∟
勾
股
弦
人们还发现,
在直角三角形中,
勾是6,
股是8,
勾是5,
股是12,
弦一定是13,
是不是所有的直角三角形都有这个性质呢?世界上许多数学家,先后用不同方法证明了这个结论. 我国把它称为勾股定理.
62=36,
82=64,
62+82=102
102=100
等等.
52=25,
122=144,
52+122=132
132=169
弦一定是10;
应用勾股定理
已知△ABC的三边分别是a,b,c,
若∠B=90度,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
A
B
C
选一选
应用勾股定理
讲一讲
8
6
A
B
C
求图中直角三角形的未知边的长度。
15
17
A
B
C
勾股定理,想得再多一点
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
回头再看看
通过本课时的学习,需要我们掌握:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,即
当堂达标
见导学案
探索勾股定理1
你想知道吗
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
探索勾股定理
教学目标
1.掌握用数格子(或割、补、拼等)的办法体验勾股定理的探索过程;
2.理解勾股定理反映的直角三角形的三边之间的数量关系;
3.认识勾股定理的各种探究方法.
P
R
Q
正方形P的面积 正方形Q的面积 正方形R的面积
A
B
C
9
16
?
怎么求SR的大小?
有几种方案?
如图,小方格的边长为1.
P
Q
C
R
求正方形R的面积?
用“补”的方法
SR
P
Q
C
R
用“割”的方法
Q
SR
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
(1)在图中,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是____个
单位面积.
正方形C的面积是_____
个单位面积.
9
9
9
18
(2)(3)
探究勾股定理
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
把正方形C分割成若干个直角边为整数的三角形来求
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
(单位面积)
把正方形C可以看成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?图2呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
A
B
C
图1
A
B
C
图2
(1)观察图1、图2,并填写右表:
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1
图2
16
9
25
4
9
13
做一做
A
B
C
图1
A
B
C
图2
(2)右图中正方形A,B,C的面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
A
B
C
SA=a2
SB=b2
SC=c2
a
b
c
a2+b2=c2
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
SA+SB=SC
探索勾股定理
中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.
据《周髀算经》记载,西周战国时期(约公元1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.
3
4
5
∟
勾
股
弦
人们还发现,
在直角三角形中,
勾是6,
股是8,
勾是5,
股是12,
弦一定是13,
是不是所有的直角三角形都有这个性质呢?世界上许多数学家,先后用不同方法证明了这个结论. 我国把它称为勾股定理.
62=36,
82=64,
62+82=102
102=100
等等.
52=25,
122=144,
52+122=132
132=169
弦一定是10;
应用勾股定理
已知△ABC的三边分别是a,b,c,
若∠B=90度,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
A
B
C
选一选
应用勾股定理
讲一讲
8
6
A
B
C
求图中直角三角形的未知边的长度。
15
17
A
B
C
勾股定理,想得再多一点
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
回头再看看
通过本课时的学习,需要我们掌握:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,即
当堂达标
见导学案
