3.1.2探索勾股定理2 课件(共17张PPT)
文档属性
| 名称 | 3.1.2探索勾股定理2 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 872.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
探索勾股定理2
教学目标
1.掌握运用勾股定理解决一些实际问题的方法;
2.理解勾股定理的多种方法验证。
c
a
b
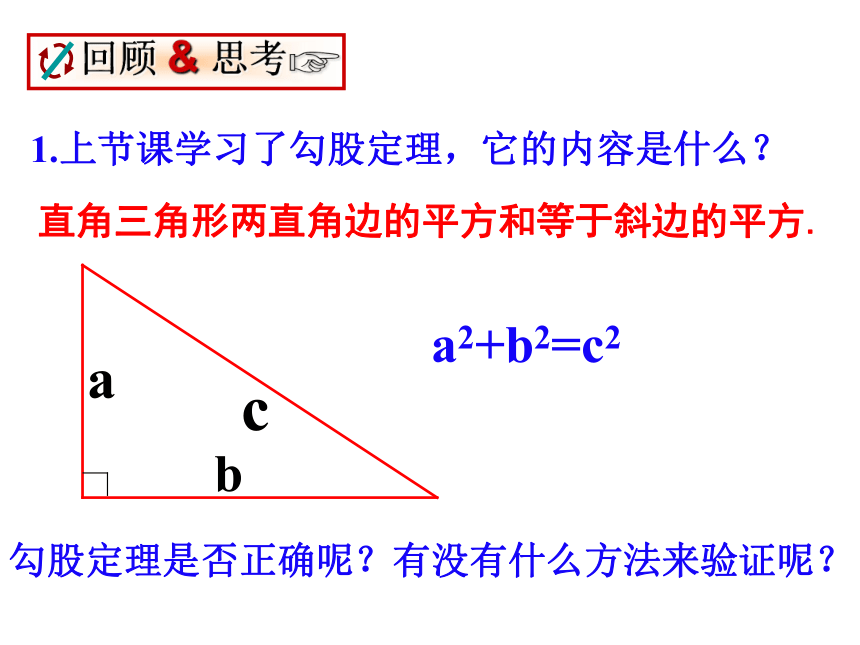
1.上节课学习了勾股定理,它的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.
a2+b2=c2
回顾 & 思考
勾股定理是否正确呢?有没有什么方法来验证呢?
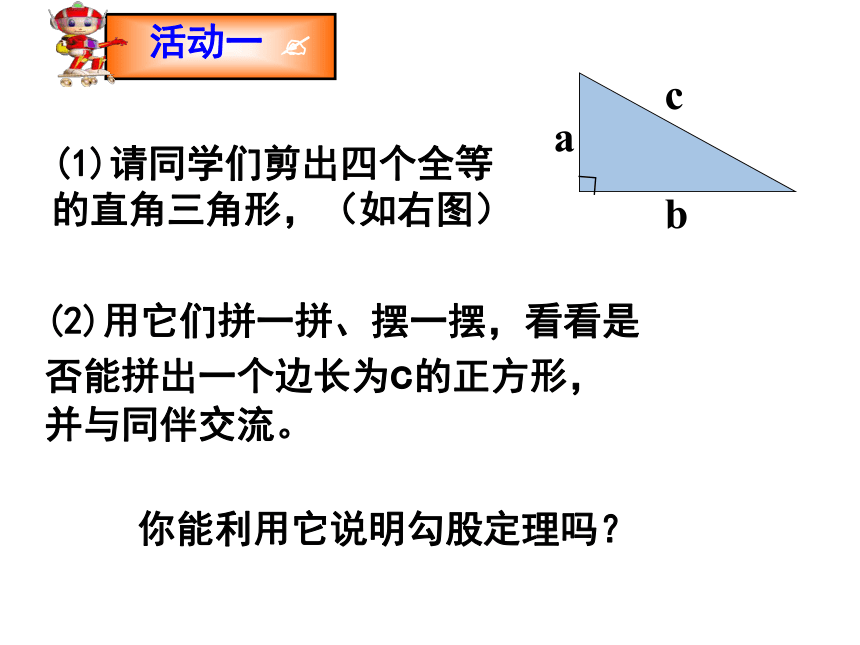
(1)请同学们剪出四个全等的直角三角形,(如右图)
∟
a
b
c
(2)用它们拼一拼、摆一摆,看看是否能拼出一个边长为c的正方形,并与同伴交流。
活动一
你能利用它说明勾股定理吗?
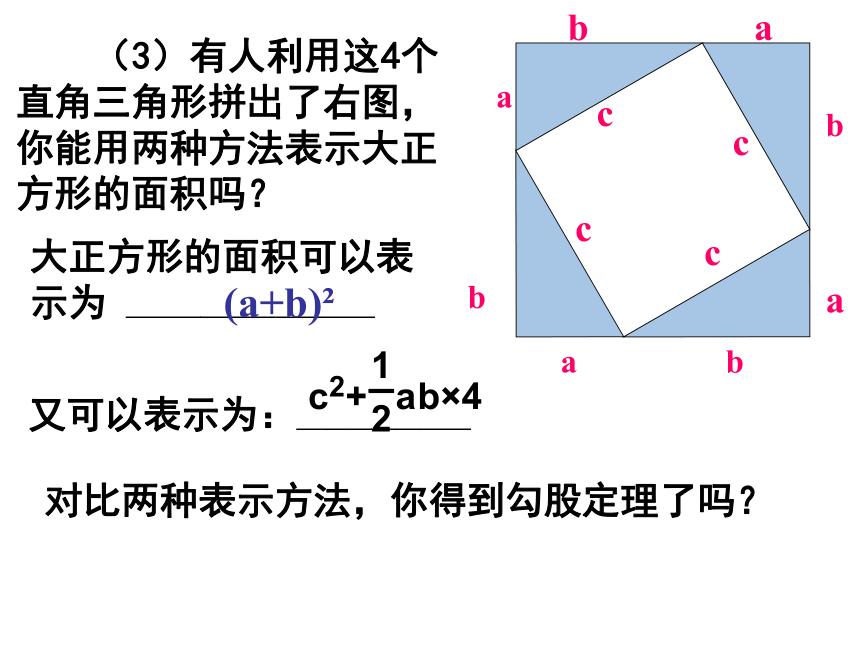
(3)有人利用这4个直角三角形拼出了右图,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为 ——————————
又可以表示为:———————
a
a
a
a
b
b
b
b
c
c
c
c
对比两种表示方法,你得到勾股定理了吗?
(a+b)
走进数学史
b
a
c
s2
s1
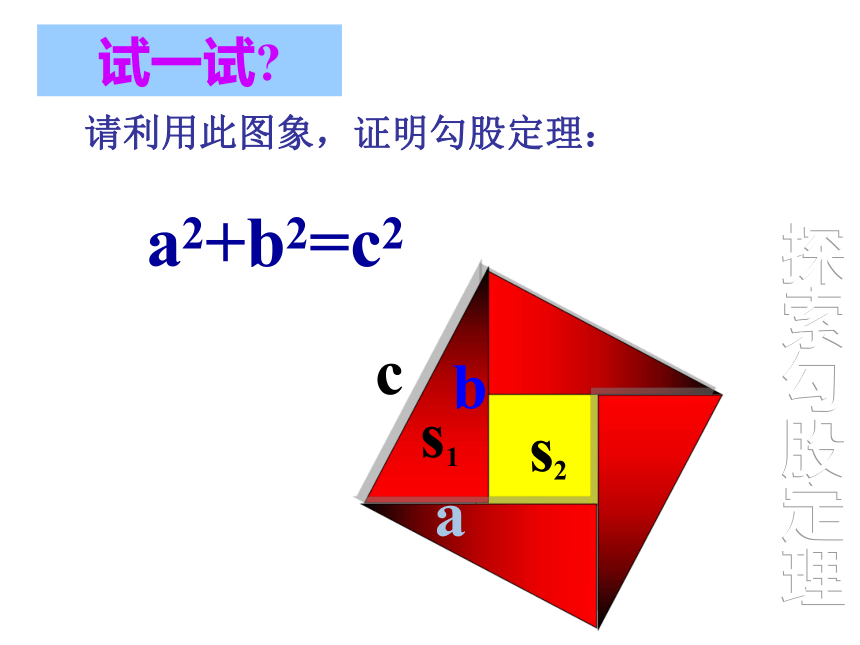
试一试
请利用此图象,证明勾股定理:
a2+b2=c2
探索勾股定理
美国第二十任总统伽菲尔德
总统巧证勾股定理
a
a
b
b
c
c
A
D
C
B
E
返回
勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
现在在网络上看到较多的是16种,包括前面的6种,还有:
欧几里得证明、 利用相似三角形性质证明、
杨作玫证明、 李锐证明、
利用切割线定理证明、 利用多列米定理证明、
作直角三角形的内切圆证明、利用反证法证明、
辛卜松证明、 陈杰证明。
走进数学史
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?
A
B
C
学以致用
4000米
5000米
20秒后
如图,一根旗杆在离地面9米处折裂,旗杆顶部落在离旗杆底部12米处.旗杆原来有多高
12米
9米
练习
议一议
a
b
c
(1)
b
a
c
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
活动二
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
在 ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则 ABC为直角三角形;
若a2 +b2>c2, 则 ABC为锐角三角形;
若a2 +b2课堂练习: 一判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为_____,斜边为上的高为______.
(2)一个零件的形状如图,
已知:AC=3cm,AB=4cm,BD=12cm,求CD
3
4
12
内容总结:
(1)运用勾股定理的条件是什么?
(2)勾股定理揭示了直角三角形的什么关系?
(3)勾股定理有什么用途?
方法总结:
用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。
当堂达标
见导学案
探索勾股定理2
教学目标
1.掌握运用勾股定理解决一些实际问题的方法;
2.理解勾股定理的多种方法验证。
c
a
b
1.上节课学习了勾股定理,它的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.
a2+b2=c2
回顾 & 思考
勾股定理是否正确呢?有没有什么方法来验证呢?
(1)请同学们剪出四个全等的直角三角形,(如右图)
∟
a
b
c
(2)用它们拼一拼、摆一摆,看看是否能拼出一个边长为c的正方形,并与同伴交流。
活动一
你能利用它说明勾股定理吗?
(3)有人利用这4个直角三角形拼出了右图,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为 ——————————
又可以表示为:———————
a
a
a
a
b
b
b
b
c
c
c
c
对比两种表示方法,你得到勾股定理了吗?
(a+b)
走进数学史
b
a
c
s2
s1
试一试
请利用此图象,证明勾股定理:
a2+b2=c2
探索勾股定理
美国第二十任总统伽菲尔德
总统巧证勾股定理
a
a
b
b
c
c
A
D
C
B
E
返回
勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
现在在网络上看到较多的是16种,包括前面的6种,还有:
欧几里得证明、 利用相似三角形性质证明、
杨作玫证明、 李锐证明、
利用切割线定理证明、 利用多列米定理证明、
作直角三角形的内切圆证明、利用反证法证明、
辛卜松证明、 陈杰证明。
走进数学史
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?
A
B
C
学以致用
4000米
5000米
20秒后
如图,一根旗杆在离地面9米处折裂,旗杆顶部落在离旗杆底部12米处.旗杆原来有多高
12米
9米
练习
议一议
a
b
c
(1)
b
a
c
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
活动二
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
在 ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则 ABC为直角三角形;
若a2 +b2>c2, 则 ABC为锐角三角形;
若a2 +b2
ABC面积为_____,斜边为上的高为______.
(2)一个零件的形状如图,
已知:AC=3cm,AB=4cm,BD=12cm,求CD
3
4
12
内容总结:
(1)运用勾股定理的条件是什么?
(2)勾股定理揭示了直角三角形的什么关系?
(3)勾股定理有什么用途?
方法总结:
用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。
当堂达标
见导学案
