19.2.3一次函数与方程、不等式 课件(共41张PPT)
文档属性
| 名称 | 19.2.3一次函数与方程、不等式 课件(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 27.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 13:47:00 | ||
图片预览








文档简介
(共41张PPT)
19.2.3一次函数与方程、不等式
第19章 一次函数
教师
xxx
人教版 八年级下册
一次函数与一元一次方程
一次函数与二元一次方程(组)
一次函数与不等式
01
03
02
CONTANTS
目 录
一次函数与一元一次方程
01
我们就从函数的角度看一下方程与不等式.
谁对呢?
视角不同,即使同一个东西看在眼里也是不同的.这次
情景引入
下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
小组合作
1.独立思考,进行解释;
2.两人一组,交流思路.
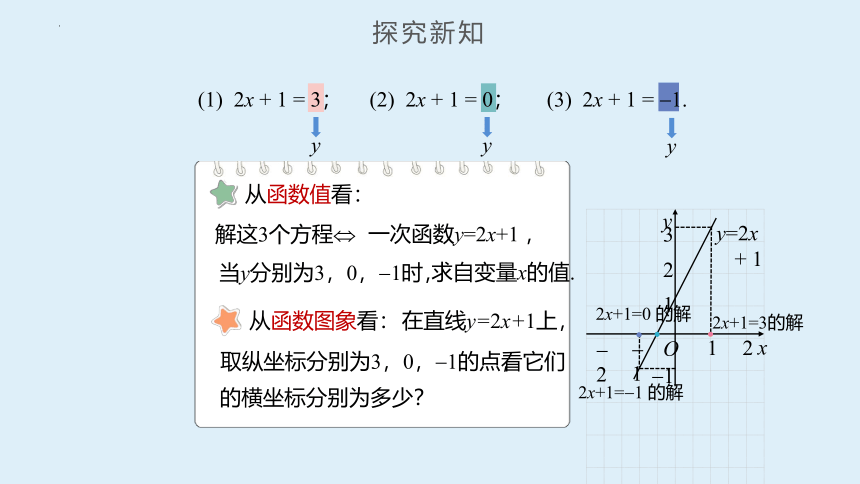
(1) 2x + 1 = 3; (2) 2x + 1 = 0; (3) 2x + 1 = 1.
探究新知
y
y
y
解这3个方程
一次函数y=2x+1 ,
当y分别为3,0, 1时,
求自变量x的值.
O
1
2
1
2
3
1
2
1
y=2x + 1
2x+1=3的解
2x+1=0 的解
2x+1= 1 的解
从函数值看:
从函数图象看:
在直线y=2x+1上,
取纵坐标分别为3,0, 1的点,
的横坐标分别为多少?
看它们
x
y
(1) 2x + 1 = 3; (2) 2x + 1 = 0; (3) 2x + 1 = 1.
探究新知
问题1:你能把得到的结论推广到一般情况吗?
y=ax+b
求一次函数y=4x+5的函数值
为9时,自变量的值.
的解就是当函数 的函数值为 时的自变
一般地,一元一次方程ax+b=c(a、b、c为常数,a≠0)
量 的值.
如:
求4x+5=9的解
c
x
探究新知
问题2:我们知道任何一元一次方程都可以转化为ax+b=0的形式,你能用函数的观点解释这个方程吗?
一元一次方程ax+b=0的解
从“函数值” 看
一次函数y=ax+b的函数值为0时,x的值.
从“函数图象”看
直线y=ax+b(a≠0)与x轴交点的横坐标.
O
x
y
y=ax+b
ax+b=0的解
探究新知
一次函数与不等式
02
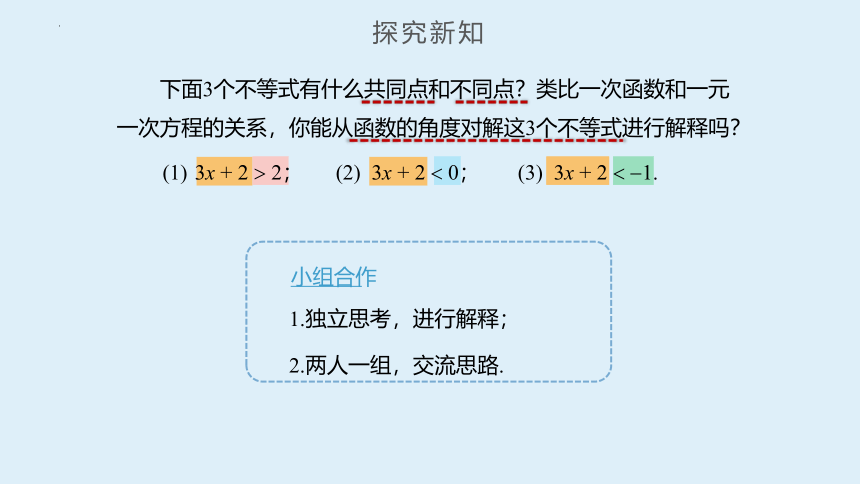
下面3个不等式有什么共同点和不同点?类比一次函数和一元一次方程的关系,你能从函数的角度对解这3个不等式进行解释吗?
小组合作
1.独立思考,进行解释;
2.两人一组,交流思路.
3x + 2 2; (2) 3x + 2 0; (3) 3x + 2 1.
探究新知
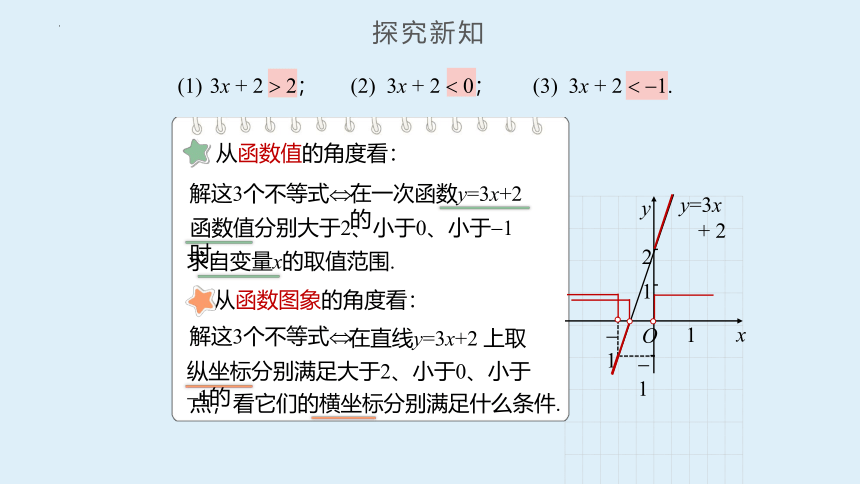
从函数值的角度看:
解这3个不等式
在一次函数y=3x+2 的
函数值分别大于2、小于0、小于 1时,
求自变量x的取值范围.
从函数图象的角度看:
解这3个不等式
在直线y=3x+2 上取
纵坐标分别满足大于2、小于0、小于 1的
点,看它们的横坐标分别满足什么条件.
O
1
1
2
1
1
y=3x + 2
3x + 2 2; (2) 3x + 2 0; (3) 3x + 2 1.
x
y
探究新知
问题1:你能把得到的结论推广到一般情况吗?
y=ax+b
求一次函数y=4x+5的函数值
小于9时,自变量x的取值范围.
数值 (或小于c)时,对应自变量的取值范围.
解不等式ax+b c(或者 c)就是求函数 的函
如:
求4x+5 9的解集
大于c
探究新知
我们知道任何一元一次不等式都可以转化为ax+b 0(或者小于0)的形式,所以:
一元一次方程ax+b 0(或 0)的解
从“函数值”看
一次函数y=ax+b的函数值大(小)于 0时,
从“函数图象”看
直线y=ax+b(a≠0)在x轴上(下)方的部分所
x的取值范围.
对应的x的取值范围.
O
x
y
y=ax+b
ax+b 0的解集
ax+b 0的解集
探究新知
【例1】一次函数y=3x b的图象与x轴交于点(1,0),则方程
3x b=0的解为 ,b= .
【解析】
①∵一次函数y=3x b的图象与x轴交于点(1,0)
∴方程3x b=0的解为x=1.
(方程3x b=0的解 直线y=3x b与x轴交点的横坐标)
x=1
②将点(1,0)代入函数y=3x b得,3×1 b=0,
解得b=3.
3
典型例题
【例2】如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式ax+b<0的解集是 .
O
2
1
x
y
A
B
不等式ax+b<0
【解析】
直线y=ax+b在x轴下方的部分所对应的x的取值范围.
x 2
求不等式的解集反应在函数图象上,
即求自变量的取值范围.
典型例题
【例3】如图,一次函数y=kx+b(k,b为常数,且k≠0)与正比例函数y=ax(a为常数,且a≠0)的图象相交于点P,则不等式kx+b ax的解集是 .
O
2
1
x
y
P
y=kx+b
y=ax
【解析】
解决此类问题一般不求函数的解析式,
而是根据不等式找到对应部分的图象,
进而确定自变量的取值范围.
不等式kx+b ax的解集
求一次函数
y=kx+b的图象在y=ax的上方时,所对
x 2
应的x的取值范围.
典型例题
一次函数与二元一次方程(组)
03
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.请用式子分别表示两个气球所在位置的海拔 y(单位:m)关于上升时间 x(单位:min)的函数关系.
1号探测气球,y关于x的函数解析式为:
解:
y=x+5
(0≤x≤60)
2号探测气球,y关于x的函数解析式为:
y=0.5x+15
(0≤x≤60)
探究新知
问题1:如果把两个式子: y=x+5,y=0.5x+15 中的变量都看作未知数,那么这两个式子表示什么意义?
【分析】
一次函数y=x+5
用方程观点看
二元一次方程x y= 5
一次函数y=0.5x+15
用方程观点看
二元一次方程0.5x y=15
那具体是怎样联系的呢?
密切联系
探究新知
一次函数
请你写出3个一次函数,用方程观点看式子,有什么发现?再写3个二元一次方程,如果把未知数看作变量,变量间的关系是什么?
用方程观点看
(变量→未知数)
y=2x+4
y=4x 5
y= 7x+1
2x y= 4
4x y=5
7x+y=1
二元一次方程
二元一次方程
用函数观点看
(未知数→变量)
6x y=4
y+4x= 5
y 7x=1
y=6x 4
y= 4x 5
y=7x+1
一次函数
互相转化
用函数观点看
用方程观点看
探究新知
问题2:如果从形的角度看,它们之间又有什么联系呢?
在同一坐标系内,(1)画出y=x+5的图象;(2)画出以方程x y= 5的5个解为坐标的点.你有什么发现?
方程x y= 5的解:
①x= 1,y=4.
( 1,4)
②x= 2,y=3.
( 2,3)
③x=0,y=5.
(0,5)
④x=1,y=6.
(1,6)
⑤x=3,y=8.
(3,8)
x
y
o
2
4
6
8
2
4
8
2
y=x+5
x
y
o
6
…
探究新知
以方程x y= 5的解为坐标的点都在一次函数y=x+5的图象上,
一次函数y=x+5
二元一次方程x y= 5
直线y=x+5
用方程观点看
用函数观点看
点的坐标满足函数解析式
以满足函数解析式的数对为坐标画点
函数y=x+5图象上的点的坐标都是二元一次方程y=x+5的解.
探究新知
一次函数与二元一次方程的关系
一般地,因为每个含有未知数x和y的二元一次方
实质:
程,都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
口诀:坐标是解, 解是坐标.
探究新知
一次函数与二元一次方程的关系
一般地,因为每个含有未知数x和y的二元一次方
实质:
程,都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
口诀:坐标是解, 解是坐标.
探究新知
问题3:在某时刻两气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?你会从数和形两方面进行研究吗?
(1)数量关系的角度
对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.
由此可得:
y=x+5
y=0.5x+15
即
x y== 5
0.5x y= 15
解得
x=20
y=25
因此,气球上升20分钟时,它们的高度相同,都是25m.
我们知道含有相同未知数的二元一次方程组成的方程组一般有一个解,那么从函数的观点看,这有什么含义?让我们还是从气球的上升问题说起.
探究新知
问题3:在某时刻两气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?你会从数和形两方面进行研究吗?
(2)图形的角度
在同一坐标系中画出两个函数的图象,如右图.
x/min
o
y/m
y=x+5
y=0.5x+15
20
25
发现:
说明:
这两条直线的交点坐标
为(20,25)
当上升20min时,两个
气球都位于海拔25m的高度.
由上可知,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.
一次函数与二元一次方程组的关系
解二元一次方程组
数:
求自变量为何值时,相应的
两个一次函数的值相等,以及这个函数值是多少.
形:
二元一次方程组的解 两条相应直线交点的坐标
探究新知
【分析】
【例4】下列各图象上点的坐标都是二元一次方程x 2y=2的解的是 ( ).
A
B
C
D
二元一次方程x 2y=2 一次函数y=x 1
令x=0,得y= 1;令y=0,得x=2.故函数与坐标轴得交点分别为(0, 1)、(2,0).
C
典型例题
【例5】请用图象法求方程组 的解.
2x y+2=0
x+y= 1
解:
方程组整理,得
y=2x+2
y= x 1
建立平面直角坐标系,分别作出
一次函数y= x 1与y=2x+2的图象,
如右图所示.
x
y
o
2
4
6
8
2
4
8
2
x
y
o
2
4
6
8
2
4
6
8
2
y=2x+2
y= x 1
2
则原方程组的解为
y=0
x= 1
转化
画图象
找交点
典型例题
【分析】
【例6】方程组 解的情况如何?你能从函数的角度解释一下吗?
x+y=5
x+y=2
x+y=5
x+y=2
解二元一次方程
确定直线y= x+2与直线y= x+5
的交点
两直线平行
方程组
x+y=5
x+y=2
无解
x
y
o
2
4
6
8
2
4
8
2
x
y
o
2
4
6
8
2
4
6
8
2
y= x+2
y= x+5
图象之间有何关系
典型例题
你能从中“悟”出些什么吗?
x
y
o
2
4
6
8
2
4
8
2
x
y
o
2
4
6
8
2
4
6
8
2
y= x+2
y= x+5
(1)二元一次方程组无解对应一次函数的图象______(无交点);
平行
(2)二元一次方程组有一解 对应一次函数的图象_____(有一个交点);
相交
(3)二元一次方程组有无数解 一次函数的图象______(有无数个交点);
重合
探究新知
C
1.已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( )
A.x=1
B.x=
C.x=-
D.x=-1
课堂练习
2.如图,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
x=2
课堂练习
3.如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式kx+b<0的解集是 .
x<-3
课堂练习
4.如图是一次函数y=kx+b(k,b为常数,且k≠0)的图象,根据图象信息求关于x的方程kx+b=4的解.
解:由图象求得一次函数解析式为y=x+1,令y=x+1=4,解得x=3,即方程kx+b=4的解是x=3.
课堂练习
5.若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
A.2 B.4
C.6 D.8
B
课堂练习
6.在同一平面直角坐标系内画出二元一次方程2x-y-2=0和x-y+3=0所对应的一次函数的图象.利用图象求:
(1)方程2x-2=x+3的解;
(2)方程组 的解.
分析:首先画出y=2x-2,y=x+3的图象.
(1)求方程的解看两直线的交点的横坐标的值.
(2)求方程组的解看两直线的交点,x=横坐标的值,y=纵坐标的值.
课堂练习
解:画出y=2x-2和y=x+3的图象,如图所示.
(1)根据图象可知方程2x-2=x+3的解为x=5.
(2)根据图象可知方程组
的解
为
课堂练习
一次函数与一元一次方程、不等式
函数与方程
函数与不等式
函数值
函数图象
函数值
函数图象
y=0时x的值
与x轴交点横坐标
x的取值范围
x轴上方或下方
课堂小结
一次函数与二元一次方程组的关系:
(1)二元一次方程组中的每个方程均可看作函数解析式.
(2)求二元一次方程组的解可看作求两个一次函数的交点坐标.
课堂小结
感谢观看
19.2.3一次函数与方程、不等式
第19章 一次函数
教师
xxx
人教版 八年级下册
一次函数与一元一次方程
一次函数与二元一次方程(组)
一次函数与不等式
01
03
02
CONTANTS
目 录
一次函数与一元一次方程
01
我们就从函数的角度看一下方程与不等式.
谁对呢?
视角不同,即使同一个东西看在眼里也是不同的.这次
情景引入
下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
小组合作
1.独立思考,进行解释;
2.两人一组,交流思路.
(1) 2x + 1 = 3; (2) 2x + 1 = 0; (3) 2x + 1 = 1.
探究新知
y
y
y
解这3个方程
一次函数y=2x+1 ,
当y分别为3,0, 1时,
求自变量x的值.
O
1
2
1
2
3
1
2
1
y=2x + 1
2x+1=3的解
2x+1=0 的解
2x+1= 1 的解
从函数值看:
从函数图象看:
在直线y=2x+1上,
取纵坐标分别为3,0, 1的点,
的横坐标分别为多少?
看它们
x
y
(1) 2x + 1 = 3; (2) 2x + 1 = 0; (3) 2x + 1 = 1.
探究新知
问题1:你能把得到的结论推广到一般情况吗?
y=ax+b
求一次函数y=4x+5的函数值
为9时,自变量的值.
的解就是当函数 的函数值为 时的自变
一般地,一元一次方程ax+b=c(a、b、c为常数,a≠0)
量 的值.
如:
求4x+5=9的解
c
x
探究新知
问题2:我们知道任何一元一次方程都可以转化为ax+b=0的形式,你能用函数的观点解释这个方程吗?
一元一次方程ax+b=0的解
从“函数值” 看
一次函数y=ax+b的函数值为0时,x的值.
从“函数图象”看
直线y=ax+b(a≠0)与x轴交点的横坐标.
O
x
y
y=ax+b
ax+b=0的解
探究新知
一次函数与不等式
02
下面3个不等式有什么共同点和不同点?类比一次函数和一元一次方程的关系,你能从函数的角度对解这3个不等式进行解释吗?
小组合作
1.独立思考,进行解释;
2.两人一组,交流思路.
3x + 2 2; (2) 3x + 2 0; (3) 3x + 2 1.
探究新知
从函数值的角度看:
解这3个不等式
在一次函数y=3x+2 的
函数值分别大于2、小于0、小于 1时,
求自变量x的取值范围.
从函数图象的角度看:
解这3个不等式
在直线y=3x+2 上取
纵坐标分别满足大于2、小于0、小于 1的
点,看它们的横坐标分别满足什么条件.
O
1
1
2
1
1
y=3x + 2
3x + 2 2; (2) 3x + 2 0; (3) 3x + 2 1.
x
y
探究新知
问题1:你能把得到的结论推广到一般情况吗?
y=ax+b
求一次函数y=4x+5的函数值
小于9时,自变量x的取值范围.
数值 (或小于c)时,对应自变量的取值范围.
解不等式ax+b c(或者 c)就是求函数 的函
如:
求4x+5 9的解集
大于c
探究新知
我们知道任何一元一次不等式都可以转化为ax+b 0(或者小于0)的形式,所以:
一元一次方程ax+b 0(或 0)的解
从“函数值”看
一次函数y=ax+b的函数值大(小)于 0时,
从“函数图象”看
直线y=ax+b(a≠0)在x轴上(下)方的部分所
x的取值范围.
对应的x的取值范围.
O
x
y
y=ax+b
ax+b 0的解集
ax+b 0的解集
探究新知
【例1】一次函数y=3x b的图象与x轴交于点(1,0),则方程
3x b=0的解为 ,b= .
【解析】
①∵一次函数y=3x b的图象与x轴交于点(1,0)
∴方程3x b=0的解为x=1.
(方程3x b=0的解 直线y=3x b与x轴交点的横坐标)
x=1
②将点(1,0)代入函数y=3x b得,3×1 b=0,
解得b=3.
3
典型例题
【例2】如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式ax+b<0的解集是 .
O
2
1
x
y
A
B
不等式ax+b<0
【解析】
直线y=ax+b在x轴下方的部分所对应的x的取值范围.
x 2
求不等式的解集反应在函数图象上,
即求自变量的取值范围.
典型例题
【例3】如图,一次函数y=kx+b(k,b为常数,且k≠0)与正比例函数y=ax(a为常数,且a≠0)的图象相交于点P,则不等式kx+b ax的解集是 .
O
2
1
x
y
P
y=kx+b
y=ax
【解析】
解决此类问题一般不求函数的解析式,
而是根据不等式找到对应部分的图象,
进而确定自变量的取值范围.
不等式kx+b ax的解集
求一次函数
y=kx+b的图象在y=ax的上方时,所对
x 2
应的x的取值范围.
典型例题
一次函数与二元一次方程(组)
03
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.请用式子分别表示两个气球所在位置的海拔 y(单位:m)关于上升时间 x(单位:min)的函数关系.
1号探测气球,y关于x的函数解析式为:
解:
y=x+5
(0≤x≤60)
2号探测气球,y关于x的函数解析式为:
y=0.5x+15
(0≤x≤60)
探究新知
问题1:如果把两个式子: y=x+5,y=0.5x+15 中的变量都看作未知数,那么这两个式子表示什么意义?
【分析】
一次函数y=x+5
用方程观点看
二元一次方程x y= 5
一次函数y=0.5x+15
用方程观点看
二元一次方程0.5x y=15
那具体是怎样联系的呢?
密切联系
探究新知
一次函数
请你写出3个一次函数,用方程观点看式子,有什么发现?再写3个二元一次方程,如果把未知数看作变量,变量间的关系是什么?
用方程观点看
(变量→未知数)
y=2x+4
y=4x 5
y= 7x+1
2x y= 4
4x y=5
7x+y=1
二元一次方程
二元一次方程
用函数观点看
(未知数→变量)
6x y=4
y+4x= 5
y 7x=1
y=6x 4
y= 4x 5
y=7x+1
一次函数
互相转化
用函数观点看
用方程观点看
探究新知
问题2:如果从形的角度看,它们之间又有什么联系呢?
在同一坐标系内,(1)画出y=x+5的图象;(2)画出以方程x y= 5的5个解为坐标的点.你有什么发现?
方程x y= 5的解:
①x= 1,y=4.
( 1,4)
②x= 2,y=3.
( 2,3)
③x=0,y=5.
(0,5)
④x=1,y=6.
(1,6)
⑤x=3,y=8.
(3,8)
x
y
o
2
4
6
8
2
4
8
2
y=x+5
x
y
o
6
…
探究新知
以方程x y= 5的解为坐标的点都在一次函数y=x+5的图象上,
一次函数y=x+5
二元一次方程x y= 5
直线y=x+5
用方程观点看
用函数观点看
点的坐标满足函数解析式
以满足函数解析式的数对为坐标画点
函数y=x+5图象上的点的坐标都是二元一次方程y=x+5的解.
探究新知
一次函数与二元一次方程的关系
一般地,因为每个含有未知数x和y的二元一次方
实质:
程,都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
口诀:坐标是解, 解是坐标.
探究新知
一次函数与二元一次方程的关系
一般地,因为每个含有未知数x和y的二元一次方
实质:
程,都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
口诀:坐标是解, 解是坐标.
探究新知
问题3:在某时刻两气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?你会从数和形两方面进行研究吗?
(1)数量关系的角度
对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.
由此可得:
y=x+5
y=0.5x+15
即
x y== 5
0.5x y= 15
解得
x=20
y=25
因此,气球上升20分钟时,它们的高度相同,都是25m.
我们知道含有相同未知数的二元一次方程组成的方程组一般有一个解,那么从函数的观点看,这有什么含义?让我们还是从气球的上升问题说起.
探究新知
问题3:在某时刻两气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?你会从数和形两方面进行研究吗?
(2)图形的角度
在同一坐标系中画出两个函数的图象,如右图.
x/min
o
y/m
y=x+5
y=0.5x+15
20
25
发现:
说明:
这两条直线的交点坐标
为(20,25)
当上升20min时,两个
气球都位于海拔25m的高度.
由上可知,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.
一次函数与二元一次方程组的关系
解二元一次方程组
数:
求自变量为何值时,相应的
两个一次函数的值相等,以及这个函数值是多少.
形:
二元一次方程组的解 两条相应直线交点的坐标
探究新知
【分析】
【例4】下列各图象上点的坐标都是二元一次方程x 2y=2的解的是 ( ).
A
B
C
D
二元一次方程x 2y=2 一次函数y=x 1
令x=0,得y= 1;令y=0,得x=2.故函数与坐标轴得交点分别为(0, 1)、(2,0).
C
典型例题
【例5】请用图象法求方程组 的解.
2x y+2=0
x+y= 1
解:
方程组整理,得
y=2x+2
y= x 1
建立平面直角坐标系,分别作出
一次函数y= x 1与y=2x+2的图象,
如右图所示.
x
y
o
2
4
6
8
2
4
8
2
x
y
o
2
4
6
8
2
4
6
8
2
y=2x+2
y= x 1
2
则原方程组的解为
y=0
x= 1
转化
画图象
找交点
典型例题
【分析】
【例6】方程组 解的情况如何?你能从函数的角度解释一下吗?
x+y=5
x+y=2
x+y=5
x+y=2
解二元一次方程
确定直线y= x+2与直线y= x+5
的交点
两直线平行
方程组
x+y=5
x+y=2
无解
x
y
o
2
4
6
8
2
4
8
2
x
y
o
2
4
6
8
2
4
6
8
2
y= x+2
y= x+5
图象之间有何关系
典型例题
你能从中“悟”出些什么吗?
x
y
o
2
4
6
8
2
4
8
2
x
y
o
2
4
6
8
2
4
6
8
2
y= x+2
y= x+5
(1)二元一次方程组无解对应一次函数的图象______(无交点);
平行
(2)二元一次方程组有一解 对应一次函数的图象_____(有一个交点);
相交
(3)二元一次方程组有无数解 一次函数的图象______(有无数个交点);
重合
探究新知
C
1.已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( )
A.x=1
B.x=
C.x=-
D.x=-1
课堂练习
2.如图,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
x=2
课堂练习
3.如图,直线y=kx+b交x轴于点A,交y轴于点B,则不等式kx+b<0的解集是 .
x<-3
课堂练习
4.如图是一次函数y=kx+b(k,b为常数,且k≠0)的图象,根据图象信息求关于x的方程kx+b=4的解.
解:由图象求得一次函数解析式为y=x+1,令y=x+1=4,解得x=3,即方程kx+b=4的解是x=3.
课堂练习
5.若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
A.2 B.4
C.6 D.8
B
课堂练习
6.在同一平面直角坐标系内画出二元一次方程2x-y-2=0和x-y+3=0所对应的一次函数的图象.利用图象求:
(1)方程2x-2=x+3的解;
(2)方程组 的解.
分析:首先画出y=2x-2,y=x+3的图象.
(1)求方程的解看两直线的交点的横坐标的值.
(2)求方程组的解看两直线的交点,x=横坐标的值,y=纵坐标的值.
课堂练习
解:画出y=2x-2和y=x+3的图象,如图所示.
(1)根据图象可知方程2x-2=x+3的解为x=5.
(2)根据图象可知方程组
的解
为
课堂练习
一次函数与一元一次方程、不等式
函数与方程
函数与不等式
函数值
函数图象
函数值
函数图象
y=0时x的值
与x轴交点横坐标
x的取值范围
x轴上方或下方
课堂小结
一次函数与二元一次方程组的关系:
(1)二元一次方程组中的每个方程均可看作函数解析式.
(2)求二元一次方程组的解可看作求两个一次函数的交点坐标.
课堂小结
感谢观看
