人教版 数学 四年级下册 第五单元第5课时《四边形的内角和》精品课件(共22张ppt)
文档属性
| 名称 | 人教版 数学 四年级下册 第五单元第5课时《四边形的内角和》精品课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 966.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 12:15:31 | ||
图片预览



文档简介
(共22张PPT)
四边形的内角和
第五单元 三角形
输入标题
学习目标
让学生经历观察、思考、推理、归纳的过程,培养 学生探究推理能力,体验数学活动的探索乐趣。
经历多种方法探究四边形的内角和的过程,知道四边形的内角和是360°;
四边形的内角和
利用转化思想,探究多边形的内角和;
一级标题
输入标题
探究新知
巩固新知
课堂小结
布置作业
创设情境
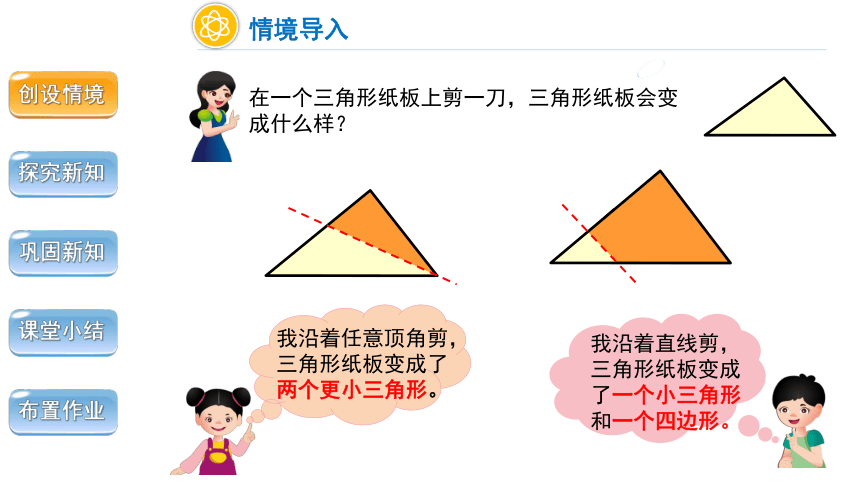
在一个三角形纸板上剪一刀,三角形纸板会变成什么样?
情境导入
我沿着直线剪,三角形纸板变成了一个小三角形和一个四边形。
我沿着任意顶角剪,三角形纸板变成了两个更小三角形。
一级标题
输入标题
探究新知
巩固新知
课堂小结
布置作业
创设情境
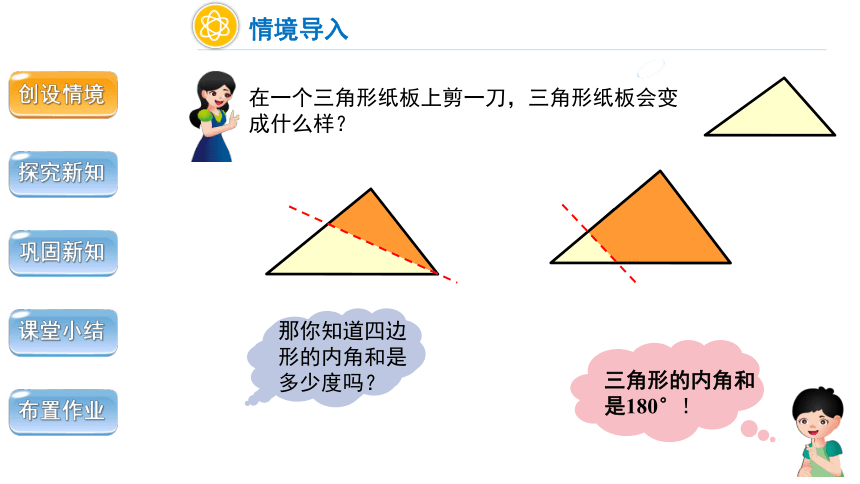
在一个三角形纸板上剪一刀,三角形纸板会变成什么样?
情境导入
三角形的内角和是180°!
三角形的内角和是多少度?
那你知道四边形的内角和是多少度吗?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
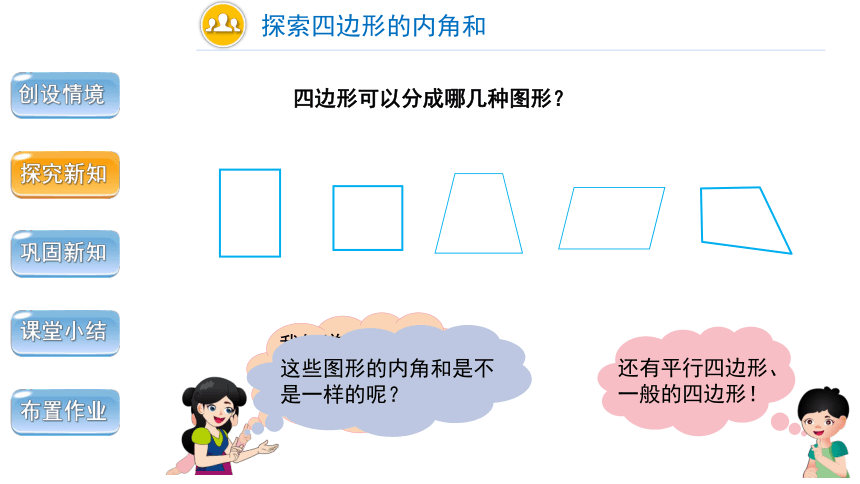
四边形可以分成哪几种图形?
还有平行四边形、一般的四边形!
我知道的四边形有:长方形、正方形,梯形……
这些图形的内角和是不是一样的呢?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
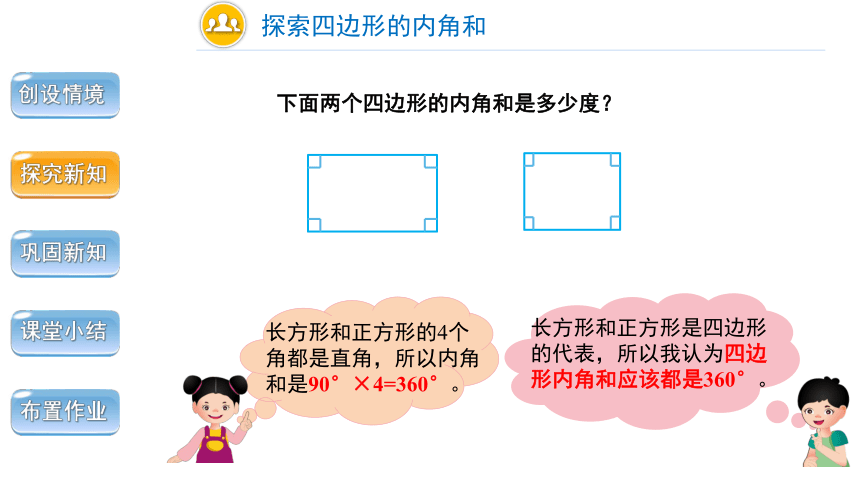
下面两个四边形的内角和是多少度?
长方形和正方形是四边形的代表,所以我认为四边形内角和应该都是360°。
长方形和正方形的4个角都是直角,所以内角和是90°×4=360°。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
长方形、正方形这两类特殊的四边形可以用求和的方法得出它的内角和,那如果是平行四边形、梯形或者一般形状的四边形,该使用什么方法来求内角和?
我可以使用“剪一剪,拼一拼”的实验方法来实现求四边形内角和。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
我把这四边形的4个角剪下来,再观察四个角组成的形状。
剪下的四个角可以拼成一个周角,而周角的度数是360°,所以四边形内角和的度数是360°。
周角
探索四边形的内角和
剪一剪,拼一拼。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
除了使用实验的方法来探索四边形内角和,还有同学有不一样的方法吗?
有!还可以通过“画一画,算一算”将四边形转化为三角形的转化方法来求。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
用虚线连接四边形两个对角顶点,可以将四边形划分成2个三角形。
180°+180°=360°
探索四边形的内角和
画一画,算一算。
四边形的内角和是360°。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
任意四边形的内角和都是360°!
通过实验、转化这两种探索四边形内角和的方法,最终可以得出什么结论?
探索四边形的内角和
非常正确!那我们再来挑战一下,多边形的内角和怎么求?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
多边形有六个顶点,,可以用转化法,分别用虚线连接六边形对角顶点,将多边形划分成4个三角形。
一个三角形的内角和是180°,四个三角形就是180°×4°=720°,这个多边形的内角和是720°。
探索多边形的内角和
你能想办法求出这个多边形的内角和吗?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
我有不同的转化法,把六边形的顶点用虚线两两相连,将多边形划分成6个三角形。
6个三角形总度数是180°×6°=1080°,
再减去中间的一个周角就是六边形的内角和,也就是1080°-360°=720°。所以这个多边形的内角和是720°。
探索多边形的内角和
你能想办法求出这个多边形的内角和吗?
答:这个多边形的内角和是720°。
周角
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
这两种方法都是运用转化法,将所求多边形的内角和转化为求几个三角形的内角和再计算,虽然分法不同,但求出的结果是一样的。
通过这两种不同方法求出的多边形内角和,你发现了什么?
探索多边形的内角和
四边形的内角和等于360°。
运用转化法,可以将求多边形的内角和转化为求几个三角形的内角和。
归纳
巩固新知
课堂小结
布置作业
探究新知
创设情境
一级标题
课堂小结
布置作业
创设情境
巩固新知
探究新知
练习
1.画一画,算一算,你发现了什么?
图形 ......
边数 3 4 5 ......
内角和 180° 180°×( ) 180°×( ) ......
2
3
6
180°×4
7
180°×5
我发现每个多边形都可以分成(“边数”-2)个三角形。
写成算式是:多边形的内角和=180 °×(边数-2)。
一级标题
课堂小结
布置作业
创设情境
巩固新知
探究新知
练习
1. 画一画,算一算,你发现了什么?
图形 ......
边数 3 4 5 ......
内角和 180 ......
180°×4-360 °
180 °×5-360 °
180 °×6-360 °
180 ° ×7-360 °
6
7
我也是把每个多边形分成三角形,但我的分法分出的三角形个数与多边形边数相同。
写成算式是:多边形的内角和=180°×边数-360°
一级标题
输入标题
课堂小结
布置作业
创设情境
这两种不同的分法得出什么结论?得出的结论相同吗?
第一种分法得出的结论是:
多边形的内角和=180°×(边数-2)
第二种分法得出的结论是:
多边形的内角和=180 ° ×边数-360°
如果用四则运算的法则,将第一种分法得出的结论去括号: 180 °×(边数-2)
=180 °×边数-360 °
第一个算式就变成了第二个算式。
所以用不同的分法得出的结论是相同的!
巩固新知
探究新知
拓展延伸
一级标题
课堂小结
布置作业
创设情境
巩固新知
探究新知
练习
2.内角和是540°的多边形是几边形?
答:内角和是540°的多边形是五边形。
解:根据多边形内角和公式:
多边形的内角和=180°×(边数-2),则540°÷180°=3,3+2=5,
所以内角和是540°的多边形是五边形。
一级标题
输入标题
布置作业
巩固新知
课堂小结
探究新知
你有什么收获?
√ 知道了四边形的内角和等于360°。
√ 能灵活运用转化法,将求多边形的内角和转化,
为求几个三角形的内角和。
创设情境
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
教材P70 第7题
创设情境
再见
四边形的内角和
第五单元 三角形
输入标题
学习目标
让学生经历观察、思考、推理、归纳的过程,培养 学生探究推理能力,体验数学活动的探索乐趣。
经历多种方法探究四边形的内角和的过程,知道四边形的内角和是360°;
四边形的内角和
利用转化思想,探究多边形的内角和;
一级标题
输入标题
探究新知
巩固新知
课堂小结
布置作业
创设情境
在一个三角形纸板上剪一刀,三角形纸板会变成什么样?
情境导入
我沿着直线剪,三角形纸板变成了一个小三角形和一个四边形。
我沿着任意顶角剪,三角形纸板变成了两个更小三角形。
一级标题
输入标题
探究新知
巩固新知
课堂小结
布置作业
创设情境
在一个三角形纸板上剪一刀,三角形纸板会变成什么样?
情境导入
三角形的内角和是180°!
三角形的内角和是多少度?
那你知道四边形的内角和是多少度吗?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
四边形可以分成哪几种图形?
还有平行四边形、一般的四边形!
我知道的四边形有:长方形、正方形,梯形……
这些图形的内角和是不是一样的呢?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
下面两个四边形的内角和是多少度?
长方形和正方形是四边形的代表,所以我认为四边形内角和应该都是360°。
长方形和正方形的4个角都是直角,所以内角和是90°×4=360°。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
长方形、正方形这两类特殊的四边形可以用求和的方法得出它的内角和,那如果是平行四边形、梯形或者一般形状的四边形,该使用什么方法来求内角和?
我可以使用“剪一剪,拼一拼”的实验方法来实现求四边形内角和。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
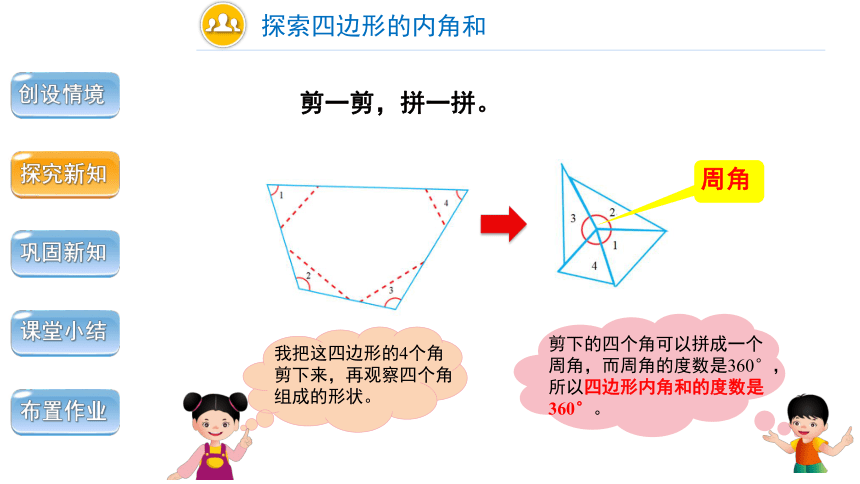
我把这四边形的4个角剪下来,再观察四个角组成的形状。
剪下的四个角可以拼成一个周角,而周角的度数是360°,所以四边形内角和的度数是360°。
周角
探索四边形的内角和
剪一剪,拼一拼。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
探索四边形的内角和
除了使用实验的方法来探索四边形内角和,还有同学有不一样的方法吗?
有!还可以通过“画一画,算一算”将四边形转化为三角形的转化方法来求。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
用虚线连接四边形两个对角顶点,可以将四边形划分成2个三角形。
180°+180°=360°
探索四边形的内角和
画一画,算一算。
四边形的内角和是360°。
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
任意四边形的内角和都是360°!
通过实验、转化这两种探索四边形内角和的方法,最终可以得出什么结论?
探索四边形的内角和
非常正确!那我们再来挑战一下,多边形的内角和怎么求?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
多边形有六个顶点,,可以用转化法,分别用虚线连接六边形对角顶点,将多边形划分成4个三角形。
一个三角形的内角和是180°,四个三角形就是180°×4°=720°,这个多边形的内角和是720°。
探索多边形的内角和
你能想办法求出这个多边形的内角和吗?
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
我有不同的转化法,把六边形的顶点用虚线两两相连,将多边形划分成6个三角形。
6个三角形总度数是180°×6°=1080°,
再减去中间的一个周角就是六边形的内角和,也就是1080°-360°=720°。所以这个多边形的内角和是720°。
探索多边形的内角和
你能想办法求出这个多边形的内角和吗?
答:这个多边形的内角和是720°。
周角
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
创设情境
这两种方法都是运用转化法,将所求多边形的内角和转化为求几个三角形的内角和再计算,虽然分法不同,但求出的结果是一样的。
通过这两种不同方法求出的多边形内角和,你发现了什么?
探索多边形的内角和
四边形的内角和等于360°。
运用转化法,可以将求多边形的内角和转化为求几个三角形的内角和。
归纳
巩固新知
课堂小结
布置作业
探究新知
创设情境
一级标题
课堂小结
布置作业
创设情境
巩固新知
探究新知
练习
1.画一画,算一算,你发现了什么?
图形 ......
边数 3 4 5 ......
内角和 180° 180°×( ) 180°×( ) ......
2
3
6
180°×4
7
180°×5
我发现每个多边形都可以分成(“边数”-2)个三角形。
写成算式是:多边形的内角和=180 °×(边数-2)。
一级标题
课堂小结
布置作业
创设情境
巩固新知
探究新知
练习
1. 画一画,算一算,你发现了什么?
图形 ......
边数 3 4 5 ......
内角和 180 ......
180°×4-360 °
180 °×5-360 °
180 °×6-360 °
180 ° ×7-360 °
6
7
我也是把每个多边形分成三角形,但我的分法分出的三角形个数与多边形边数相同。
写成算式是:多边形的内角和=180°×边数-360°
一级标题
输入标题
课堂小结
布置作业
创设情境
这两种不同的分法得出什么结论?得出的结论相同吗?
第一种分法得出的结论是:
多边形的内角和=180°×(边数-2)
第二种分法得出的结论是:
多边形的内角和=180 ° ×边数-360°
如果用四则运算的法则,将第一种分法得出的结论去括号: 180 °×(边数-2)
=180 °×边数-360 °
第一个算式就变成了第二个算式。
所以用不同的分法得出的结论是相同的!
巩固新知
探究新知
拓展延伸
一级标题
课堂小结
布置作业
创设情境
巩固新知
探究新知
练习
2.内角和是540°的多边形是几边形?
答:内角和是540°的多边形是五边形。
解:根据多边形内角和公式:
多边形的内角和=180°×(边数-2),则540°÷180°=3,3+2=5,
所以内角和是540°的多边形是五边形。
一级标题
输入标题
布置作业
巩固新知
课堂小结
探究新知
你有什么收获?
√ 知道了四边形的内角和等于360°。
√ 能灵活运用转化法,将求多边形的内角和转化,
为求几个三角形的内角和。
创设情境
一级标题
输入标题
巩固新知
课堂小结
布置作业
探究新知
教材P70 第7题
创设情境
再见
