人教版 数学 四年级下册 小数的近似数第1课时示范教学课件(共13张ppt)
文档属性
| 名称 | 人教版 数学 四年级下册 小数的近似数第1课时示范教学课件(共13张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
小数的意义和性质
小数的近似数
第 1 课时
一、新课导入
把下面各数省略万位后面的尾数,求出它们的近似数。
≈ 5 万
≈ 6 万
≈ 3 万
≈ 99 万
≈ 40 万
≈ 1 万
986534
58741
31200
50047
398010
14870
“四舍五入”法
二、探究新知
从图中你知道了哪些信息,所求的问题是什么?
小欣
0.984m
小欣高约0.98m。
小欣高约1m。
探究新知
求小数的近似数,也可以用“四舍五入”法。
求整数的近似数,可以用“四舍五入”法。
二、探究新知
1.“四舍五入”法。
二、探究新知
2. 求一个小数的近似数。
(1)保留两位小数。
0.984 m 是如何得到 0.98 m 的?
0 . 9 8 4
小于 5,舍去。
≈ 0 . 9 8
百分位
二、探究新知
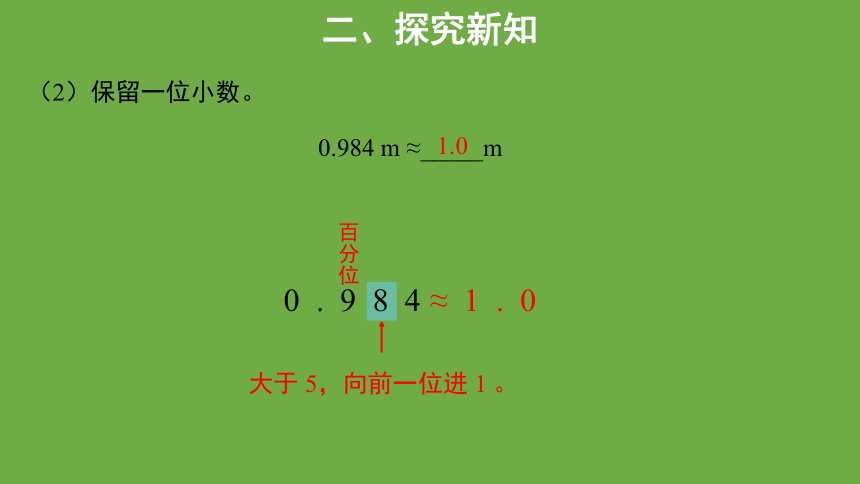
(2)保留一位小数。
0.984 m ≈_____m
0 . 9 8 4
大于 5,向前一位进 1 。
≈ 1 . 0
百分位
1.0
二、探究新知
(3)保留整数。
0.984 m ≈ 1 m
0 . 9 8 4
大于 5,向前一位进 1 。
≈ 1
个位
一个小数怎样才能保留整数呢?
二、探究新知
0 . 9 8 4 m ≈ 1 . m
0 . 9 8 4 m ≈ 1 m
0
十分位
保留一位小数
保留整数
个位
更精确
近似数末尾的 0 是不能去掉,表示近似数的精确度。
求出的两个近似数 1.0 和 1 哪个更精确些?
求小数的近似数时,可以用“四舍五入”法。
保留整数时,表示精确到个位,应根据十分位上数的大小判断是否进位;
保留一位小数时,表示精确到十分位,应根据百分位上数的大小判断是否进位;
保留两位小数时,表示精确到百分位,应根据千分位上数的大小判断是否进位……
在表示近似数时,小数末尾的 0 不能去掉。
二、探究新知
三、巩固练习
1. 求下面小数的近似数。
保留两位小数:
0.256
12.006
1.0987
保留一位小数:
3.72
0.58
9.0548
≈ 0.26
≈ 12.01
≈ 1.10
≈ 3.7
≈ 0.6
≈ 9.1
三、巩固练习
2. 小法官,我来当。
(1)近似数是 3.2 的两位小数只有一个。( )
(2)近似数 3 和 3.0 的大小相等,精确度也一样。( )
(3)近似数一定比原数大。( )
(4)保留三位小数表示精确到千分位。( )
×
√
×
×
四、课堂小结
本节课我们学习了怎样求一个小数的近似数,知道了求小数的近似数的方法与求整数的近似数相似,要用“四舍五入”法保留小数位数,保留小数位数越多,精确程度越高。
再见
小数的意义和性质
小数的近似数
第 1 课时
一、新课导入
把下面各数省略万位后面的尾数,求出它们的近似数。
≈ 5 万
≈ 6 万
≈ 3 万
≈ 99 万
≈ 40 万
≈ 1 万
986534
58741
31200
50047
398010
14870
“四舍五入”法
二、探究新知
从图中你知道了哪些信息,所求的问题是什么?
小欣
0.984m
小欣高约0.98m。
小欣高约1m。
探究新知
求小数的近似数,也可以用“四舍五入”法。
求整数的近似数,可以用“四舍五入”法。
二、探究新知
1.“四舍五入”法。
二、探究新知
2. 求一个小数的近似数。
(1)保留两位小数。
0.984 m 是如何得到 0.98 m 的?
0 . 9 8 4
小于 5,舍去。
≈ 0 . 9 8
百分位
二、探究新知
(2)保留一位小数。
0.984 m ≈_____m
0 . 9 8 4
大于 5,向前一位进 1 。
≈ 1 . 0
百分位
1.0
二、探究新知
(3)保留整数。
0.984 m ≈ 1 m
0 . 9 8 4
大于 5,向前一位进 1 。
≈ 1
个位
一个小数怎样才能保留整数呢?
二、探究新知
0 . 9 8 4 m ≈ 1 . m
0 . 9 8 4 m ≈ 1 m
0
十分位
保留一位小数
保留整数
个位
更精确
近似数末尾的 0 是不能去掉,表示近似数的精确度。
求出的两个近似数 1.0 和 1 哪个更精确些?
求小数的近似数时,可以用“四舍五入”法。
保留整数时,表示精确到个位,应根据十分位上数的大小判断是否进位;
保留一位小数时,表示精确到十分位,应根据百分位上数的大小判断是否进位;
保留两位小数时,表示精确到百分位,应根据千分位上数的大小判断是否进位……
在表示近似数时,小数末尾的 0 不能去掉。
二、探究新知
三、巩固练习
1. 求下面小数的近似数。
保留两位小数:
0.256
12.006
1.0987
保留一位小数:
3.72
0.58
9.0548
≈ 0.26
≈ 12.01
≈ 1.10
≈ 3.7
≈ 0.6
≈ 9.1
三、巩固练习
2. 小法官,我来当。
(1)近似数是 3.2 的两位小数只有一个。( )
(2)近似数 3 和 3.0 的大小相等,精确度也一样。( )
(3)近似数一定比原数大。( )
(4)保留三位小数表示精确到千分位。( )
×
√
×
×
四、课堂小结
本节课我们学习了怎样求一个小数的近似数,知道了求小数的近似数的方法与求整数的近似数相似,要用“四舍五入”法保留小数位数,保留小数位数越多,精确程度越高。
再见
