第24章 相似三角形测试卷(基础卷) 2022—2023学年 沪教版(上海)数学 九年级第二学期 含答案
文档属性
| 名称 | 第24章 相似三角形测试卷(基础卷) 2022—2023学年 沪教版(上海)数学 九年级第二学期 含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 22:17:11 | ||
图片预览

文档简介
沪教版九年级数学 第24章 相似三角形测试卷(基础卷)
一、选择题
直角三角形的重心到斜边中点的距离,与斜边的比值是
A. B. C. D.
下列命题中正确的是
A.
B.单位向量等于
C.当 时,有
D. 中,有
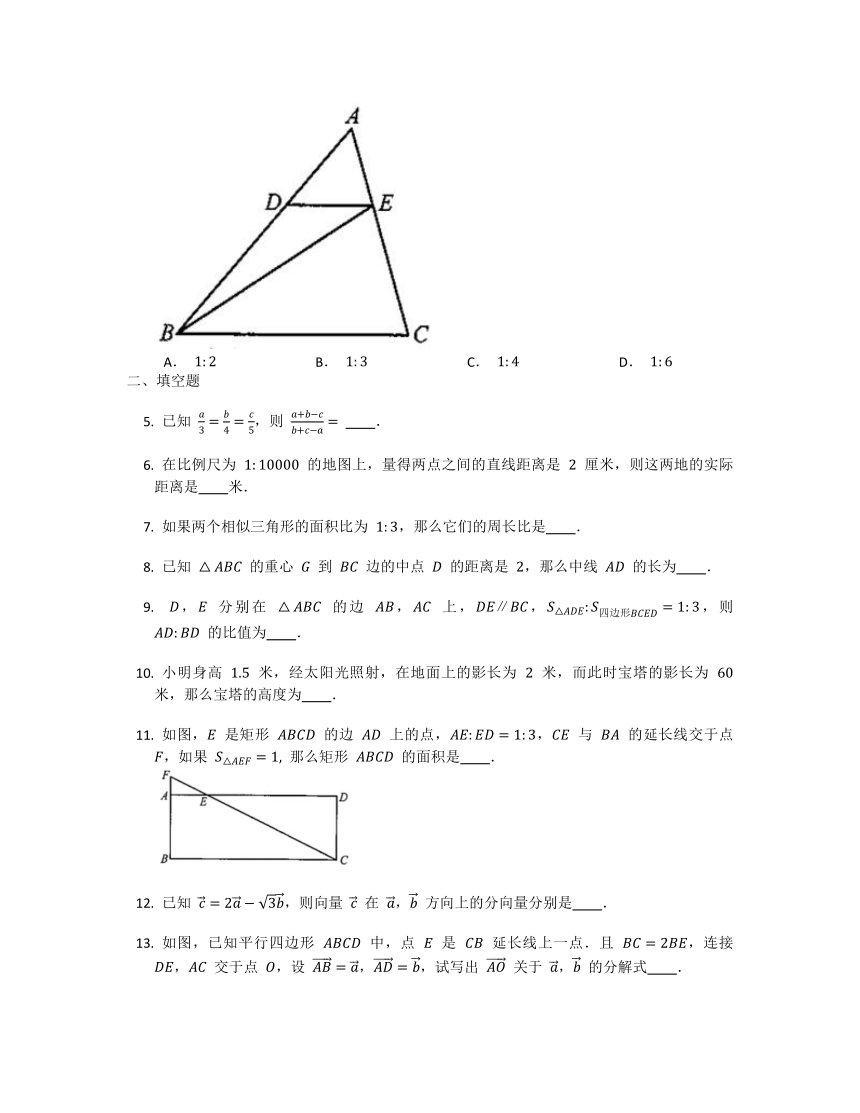
如图,在正方形 中,点 是 边上的中点, 是 边上一动点,下列条件中,不能推出 与 相似的是
A. B.
C. D.
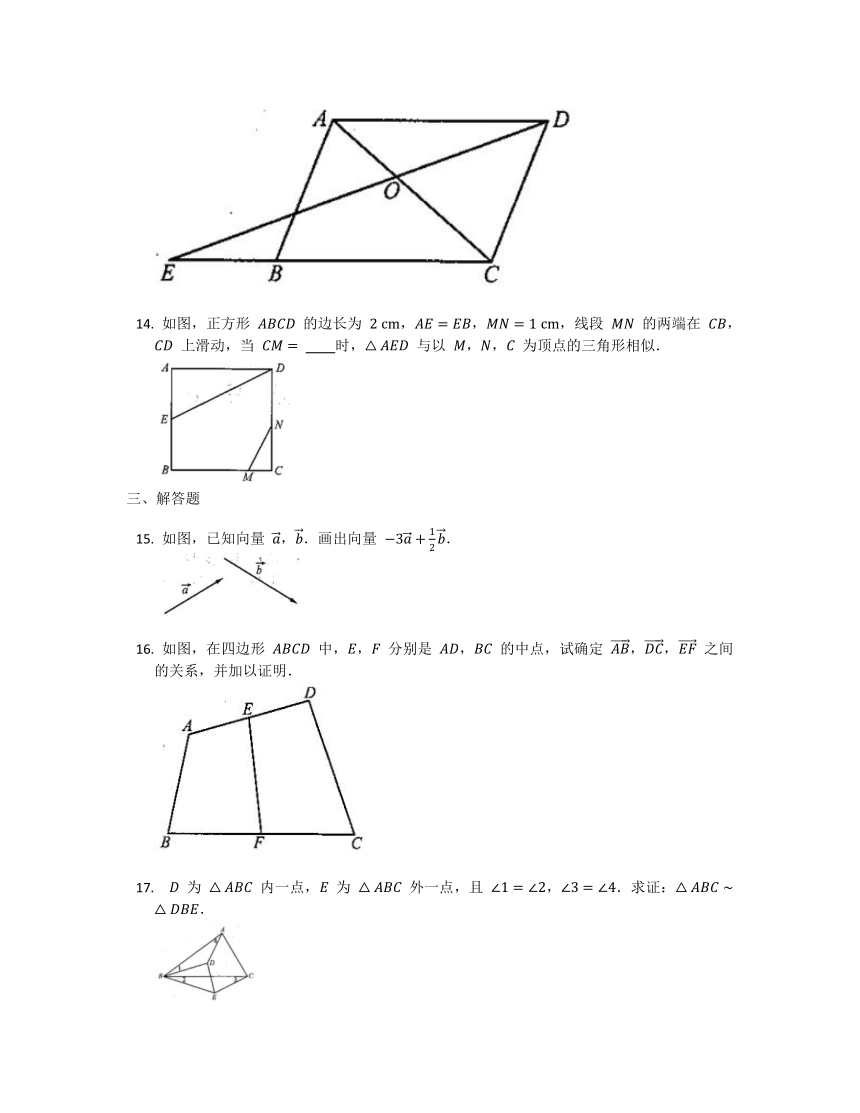
如图,在 中,点 , 分别在边 , 上,,,那么 等于
A. B. C. D.
二、填空题
已知 ,则 .
在比例尺为 的地图上,量得两点之间的直线距离是 厘米,则这两地的实际距离是 米.
如果两个相似三角形的面积比为 ,那么它们的周长比是 .
已知 的重心 到 边的中点 的距离是 ,那么中线 的长为 .
, 分别在 的边 , 上,,,则 的比值为 .
小明身高 米,经太阳光照射,在地面上的影长为 米,而此时宝塔的影长为 米,那么宝塔的高度为 .
如图, 是矩形 的边 上的点,, 与 的延长线交于点 ,如果 那么矩形 的面积是 .
已知 ,则向量 在 , 方向上的分向量分别是 .
如图,已知平行四边形 中,点 是 延长线上一点.且 ,连接 , 交于点 ,设 ,,试写出 关于 , 的分解式 .
如图,正方形 的边长为 ,,,线段 的两端在 , 上滑动,当 时, 与以 ,, 为顶点的三角形相似.
三、解答题
如图,已知向量 ,.画出向量 .
如图,在四边形 中,, 分别是 , 的中点,试确定 ,, 之间的关系,并加以证明.
为 内一点, 为 外一点,且 ,.求证:.
如图,已知在 中,,.
(1) 求证:;
(2) 当 时,求证:.
已知四边形 的对角线 , 相交于点 ,.求证:.
如图, 是 边 上的中点,且 ,垂足为 ,,.
(1) 求证:;
(2) 若 ,求四边形 的面积.
直角平面坐标系 中, 的位置如图所示,已知 ,,点 坐标为 .求:
(1) 点 坐标;
(2) 边 与 轴的交点坐标.
矩形 的边 在 的边 上,顶点 , 分别在边 , 上,,,设 ,矩形 的面积为 .求:
(1) 与 的函数关系式及定义域;
(2) 连接 ,当 为等腰三角形时,求 的值.
答案
1. 【答案】D
2. 【答案】D
3. 【答案】A
4. 【答案】B
5. 【答案】
6. 【答案】
7. 【答案】
8. 【答案】
9. 【答案】
10. 【答案】 米
11. 【答案】
12. 【答案】 和
13. 【答案】
14. 【答案】 或
15. 【答案】如图,.
16. 【答案】 .(提示:;,两式相加即可)
17. 【答案】先证明 ,
从而得到 ,
变形得到 ,
又 ,
即可证明 .
18. 【答案】
(1) 证明 ,即可得 .
(2) 证明 (两边对应成比例且夹角相等),于是得 ,易得 ,于是证得:.
19. 【答案】先证明 ,
从而得 ,
又 ,
于是可证 .
20. 【答案】
(1) 易得 ,于是 ,又 ,
所以 .
(2) .
设 ,则 ,,于是:,解得 .
21. 【答案】
(1) .
(2) .
22. 【答案】
(1) ,定义域:.
(2) 当 时,;
如考虑 ,根据勾股定理列方程 ,解出 ,
在定义域内,,不在定义域内;
如考虑 ,有 ,
则 ,也合适.
综上所述, 的值为 , 或 .
一、选择题
直角三角形的重心到斜边中点的距离,与斜边的比值是
A. B. C. D.
下列命题中正确的是
A.
B.单位向量等于
C.当 时,有
D. 中,有
如图,在正方形 中,点 是 边上的中点, 是 边上一动点,下列条件中,不能推出 与 相似的是
A. B.
C. D.
如图,在 中,点 , 分别在边 , 上,,,那么 等于
A. B. C. D.
二、填空题
已知 ,则 .
在比例尺为 的地图上,量得两点之间的直线距离是 厘米,则这两地的实际距离是 米.
如果两个相似三角形的面积比为 ,那么它们的周长比是 .
已知 的重心 到 边的中点 的距离是 ,那么中线 的长为 .
, 分别在 的边 , 上,,,则 的比值为 .
小明身高 米,经太阳光照射,在地面上的影长为 米,而此时宝塔的影长为 米,那么宝塔的高度为 .
如图, 是矩形 的边 上的点,, 与 的延长线交于点 ,如果 那么矩形 的面积是 .
已知 ,则向量 在 , 方向上的分向量分别是 .
如图,已知平行四边形 中,点 是 延长线上一点.且 ,连接 , 交于点 ,设 ,,试写出 关于 , 的分解式 .
如图,正方形 的边长为 ,,,线段 的两端在 , 上滑动,当 时, 与以 ,, 为顶点的三角形相似.
三、解答题
如图,已知向量 ,.画出向量 .
如图,在四边形 中,, 分别是 , 的中点,试确定 ,, 之间的关系,并加以证明.
为 内一点, 为 外一点,且 ,.求证:.
如图,已知在 中,,.
(1) 求证:;
(2) 当 时,求证:.
已知四边形 的对角线 , 相交于点 ,.求证:.
如图, 是 边 上的中点,且 ,垂足为 ,,.
(1) 求证:;
(2) 若 ,求四边形 的面积.
直角平面坐标系 中, 的位置如图所示,已知 ,,点 坐标为 .求:
(1) 点 坐标;
(2) 边 与 轴的交点坐标.
矩形 的边 在 的边 上,顶点 , 分别在边 , 上,,,设 ,矩形 的面积为 .求:
(1) 与 的函数关系式及定义域;
(2) 连接 ,当 为等腰三角形时,求 的值.
答案
1. 【答案】D
2. 【答案】D
3. 【答案】A
4. 【答案】B
5. 【答案】
6. 【答案】
7. 【答案】
8. 【答案】
9. 【答案】
10. 【答案】 米
11. 【答案】
12. 【答案】 和
13. 【答案】
14. 【答案】 或
15. 【答案】如图,.
16. 【答案】 .(提示:;,两式相加即可)
17. 【答案】先证明 ,
从而得到 ,
变形得到 ,
又 ,
即可证明 .
18. 【答案】
(1) 证明 ,即可得 .
(2) 证明 (两边对应成比例且夹角相等),于是得 ,易得 ,于是证得:.
19. 【答案】先证明 ,
从而得 ,
又 ,
于是可证 .
20. 【答案】
(1) 易得 ,于是 ,又 ,
所以 .
(2) .
设 ,则 ,,于是:,解得 .
21. 【答案】
(1) .
(2) .
22. 【答案】
(1) ,定义域:.
(2) 当 时,;
如考虑 ,根据勾股定理列方程 ,解出 ,
在定义域内,,不在定义域内;
如考虑 ,有 ,
则 ,也合适.
综上所述, 的值为 , 或 .
